浙江省宁波市余姚市实验学校2023-2024学年九年级A班联考数学试卷(模拟考试)(pdf、含答案)
文档属性
| 名称 | 浙江省宁波市余姚市实验学校2023-2024学年九年级A班联考数学试卷(模拟考试)(pdf、含答案) |  | |
| 格式 | |||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-09 18:01:44 | ||
图片预览


文档简介
2023 学年第一学期九年级 A 班联考——数学试题卷
一、选择题(共 10 小题,每题 3 分)
1.如图,四边形 ABCD内接于 O,若 C 130 ,则 BOD的度数为( )
A. 50 B. 100 C. 130 D. 150
2.已知 x, y, z 2 3 5 5x y满足 ,则 的值为( )
x y z z x y 2z
1 1 1
A.1 B. C. D.
3 3 2
3.如图 A、B、C在⊙O上,连接 OA、OB、OC,若∠BOC=3∠AOB,劣弧 AC
的度数是 120o,OC= 2 3.则图中阴影部分的面积是 ( )
A 1. 32 B. 2 3 C.3 2 3 D.4π-3 3
4. x 5 3设 ,则代数式 x(x 1)(x 2)(x 3)的值为( )
2
A、-1 B、1 C、0 D、2
5. 点O是 ABC的外心,也是△BCD的内心,若 A 70 ,则 BDC的度数是
( )
A. 80° B. 90° C. 100° D. 110°
6.如图 1,正方形 ABCD绕中心 O逆时针旋转 45°得到正方形 A B C D ,现将整个图形的外围
以 O为位似中心得到位似图形如图 2 1所示,位似比为 2 ,若整个图形的外围周长为 16,则图
中的阴影部分面积为( )
A.6 3 2 B. 4 2 2 C.2 2 D.8 4 2
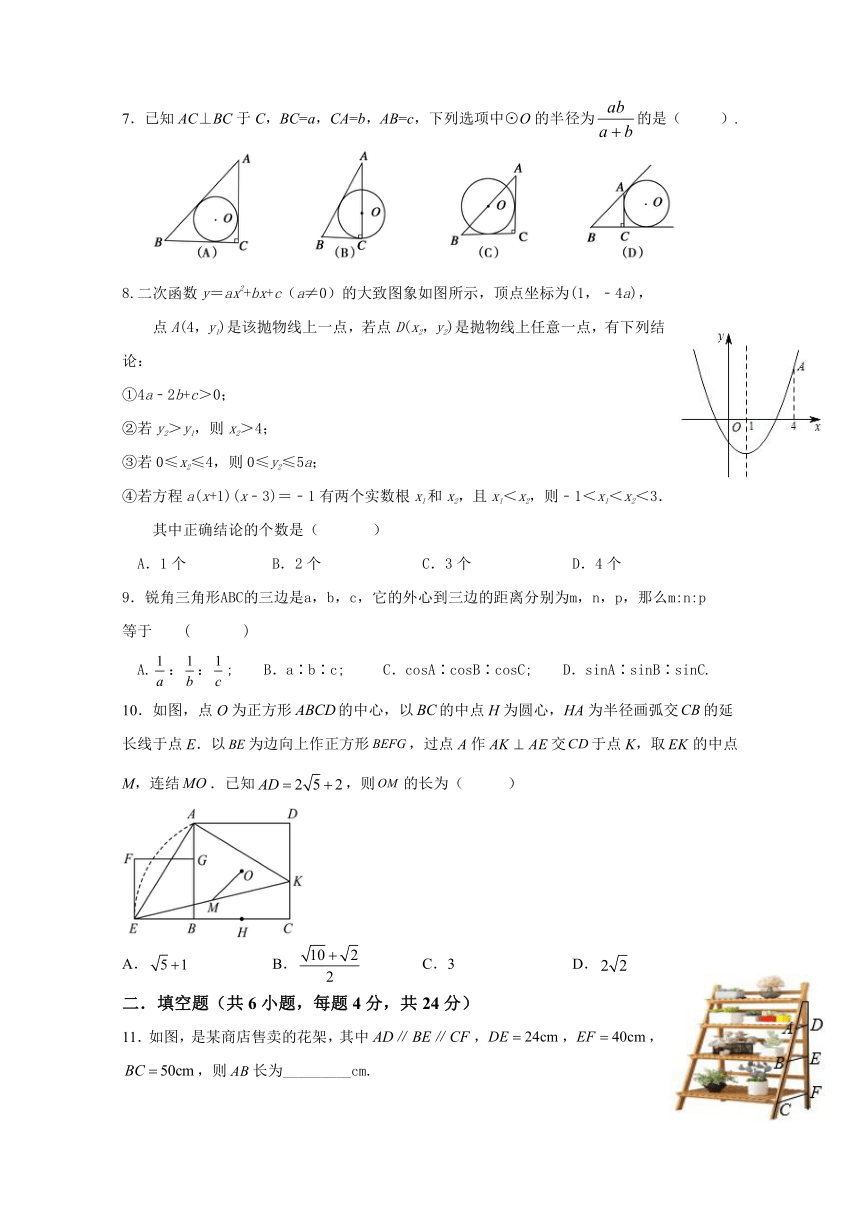
ab
7.已知 AC⊥BC于 C,BC=a,CA=b,AB=c,下列选项中⊙O的半径为 的是( ).
a b
2
8.二次函数 y=ax +bx+c(a≠0)的大致图象如图所示,顶点坐标为(1,﹣4a),
点 A(4,y1)是该抛物线上一点,若点 D(x2,y2)是抛物线上任意一点,有下列结
论:
①4a﹣2b+c>0;
②若 y2>y1,则 x2>4;
③若 0≤x2≤4,则 0≤y2≤5a;
④若方程 a(x+1)(x﹣3)=﹣1 有两个实数根 x1和 x2,且 x1<x2,则﹣1<x1<x2<3.
其中正确结论的个数是( )
A.1 个 B.2个 C.3个 D.4 个
9.锐角三角形ABC的三边是a,b,c,它的外心到三边的距离分别为m,n,p,那么m:n:p
等于 ( )
1 1 1
A. : : ; B.a∶b∶c; C.cosA∶cosB∶cosC; D.sinA∶sinB∶sinC.
a b c
10.如图,点 O为正方形 ABCD的中心,以 BC的中点 H为圆心,HA为半径画弧交CB的延
长线于点 E.以 BE为边向上作正方形 BEFG,过点 A作 AK AE交CD于点 K,取 EK 的中点
M,连结MO.已知 AD 2 5 2,则OM 的长为( )
A 5 1 B 10 2. . C.3 D. 2 2
2
二.填空题(共 6 小题,每题 4 分,共 24 分)
11.如图,是某商店售卖的花架,其中 AD∥BE∥CF,DE 24cm,EF 40cm,
BC 50cm,则 AB长为_________cm.
12.把一根长度为 6 的铁丝截成 3 段,若三段的长度均为正整数,则能构成三角形的概率为
________.
13.因为 cos60° 1= ,cos 240° 1=- ,所以 cos 240°=cos(180°+60°)=-cos 60°;由
2 2
此猜想、推理知:当α为锐角时有 cos (180°+α)=-cos α,则:cos 210°=
14.如图,在 △ 中,∠ = 90°,E为 边上一点,以 为直径的
半圆O与 相切于点D,连接 , = 3, = 3 5.P是 边上
的动点,当△ 为等腰三角形时, 的长为 .
15.图 1是一款由若干条吊链等间距悬挂而成的挂帘,吊链顶端悬挂在水
平横梁上,自然下垂时底部呈圆弧形,其中最长吊链为95cm,最短吊链为
45cm,挂满后呈轴对称分布.图 2是其示意图,其中最长两条吊链 AC与BD
之间的距离 AB为114cm.若吊链数量为偶数,记对称轴右侧最短挂链的底端为点 F,当 C,F,
B三点在同一条直线上时,吊链的数量为 .
16. 如图,已知正方形 ABCD的边长为 4,点 E是正方形内部一点,连接 EA,
EB满足 EAB EBC ,点 P是 BC边上一动点,连结 PD, PE.则
PD PE长度的最小值为
三、(共 8 小题,计 66 分)
1 1
17.(6分)计算: 8 2sin 45 (2 ) 0
3
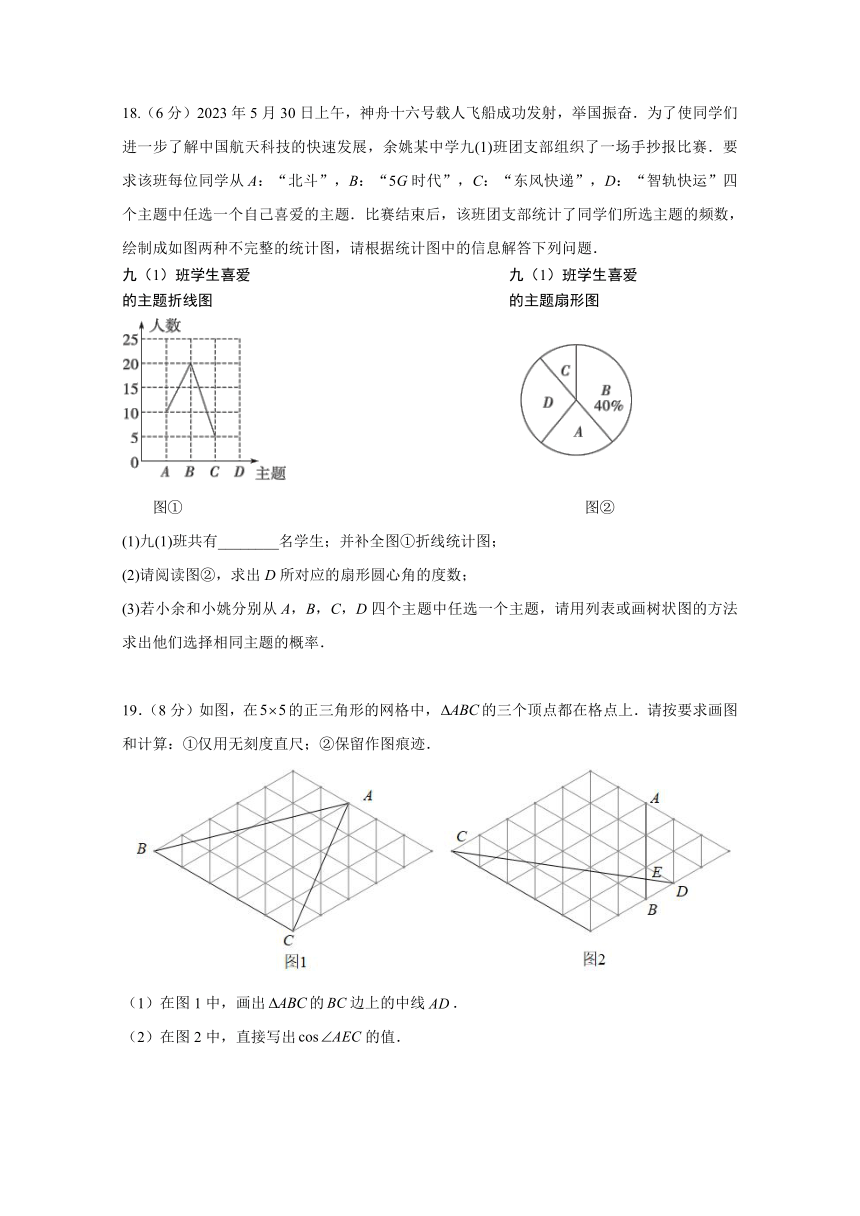
18.(6分)2023年 5月 30日上午,神舟十六号载人飞船成功发射,举国振奋.为了使同学们
进一步了解中国航天科技的快速发展,余姚某中学九(1)班团支部组织了一场手抄报比赛.要
求该班每位同学从 A:“北斗”,B:“5G时代”,C:“东风快递”,D:“智轨快运”四
个主题中任选一个自己喜爱的主题.比赛结束后,该班团支部统计了同学们所选主题的频数,
绘制成如图两种不完整的统计图,请根据统计图中的信息解答下列问题.
九(1)班学生喜爱 九(1)班学生喜爱
的主题折线图 的主题扇形图
图① 图②
(1)九(1)班共有________名学生;并补全图①折线统计图;
(2)请阅读图②,求出 D所对应的扇形圆心角的度数;
(3)若小余和小姚分别从 A,B,C,D四个主题中任选一个主题,请用列表或画树状图的方法
求出他们选择相同主题的概率.
19.(8分)如图,在5 5的正三角形的网格中, ABC的三个顶点都在格点上.请按要求画图
和计算:①仅用无刻度直尺;②保留作图痕迹.
(1)在图 1中,画出 ABC的BC边上的中线 AD.
(2)在图 2中,直接写出 cos AEC的值.
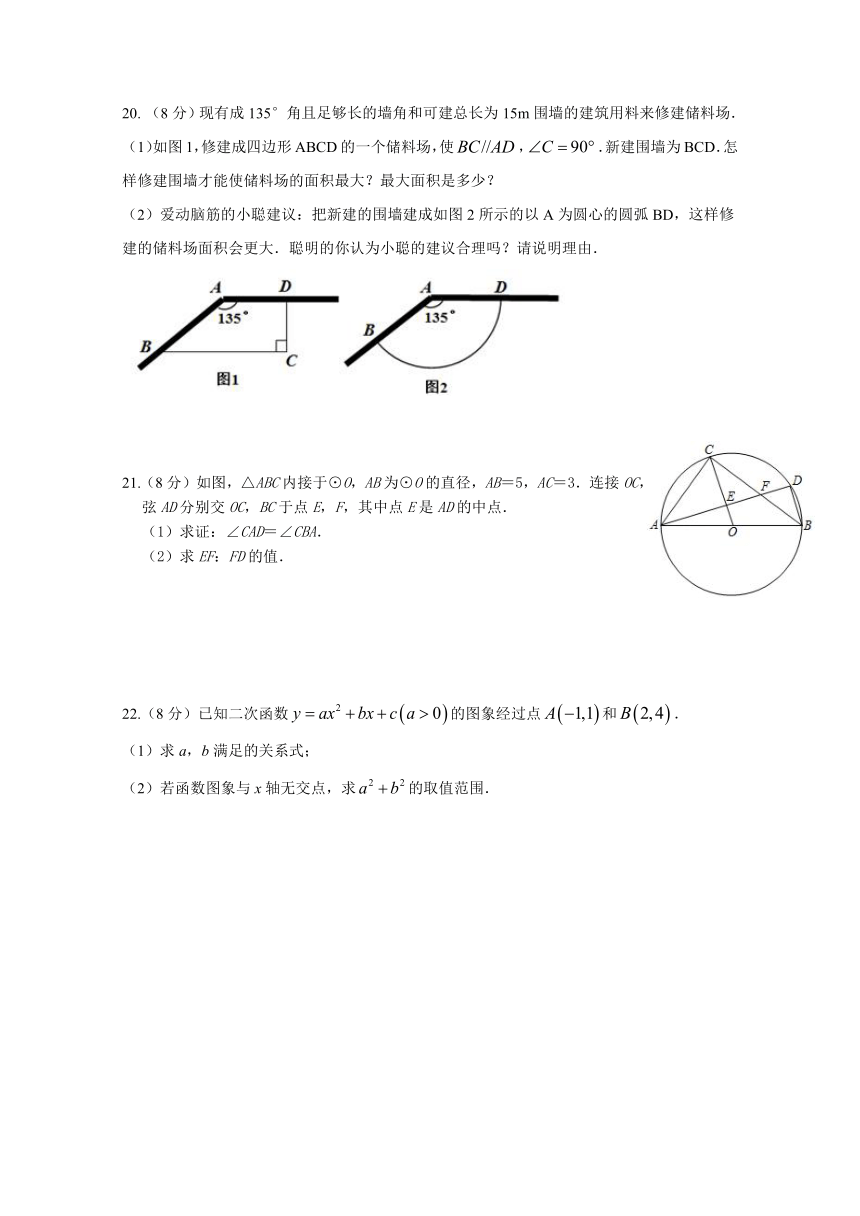
20. (8分)现有成 135°角且足够长的墙角和可建总长为 15m围墙的建筑用料来修建储料场.
(1)如图 1,修建成四边形 ABCD的一个储料场,使BC //AD, C 90 .新建围墙为 BCD.怎
样修建围墙才能使储料场的面积最大?最大面积是多少?
(2)爱动脑筋的小聪建议:把新建的围墙建成如图 2所示的以 A为圆心的圆弧 BD,这样修
建的储料场面积会更大.聪明的你认为小聪的建议合理吗?请说明理由.
21.(8分)如图,△ABC 内接于⊙O,AB 为⊙O 的直径,AB=5,AC=3.连接 OC,
弦 AD 分别交 OC,BC 于点 E,F,其中点 E是 AD 的中点.
(1)求证:∠CAD=∠CBA.
(2)求 EF:FD 的值.
22.(8 2分)已知二次函数 y ax bx c a 0 的图象经过点 A 1,1 和 B 2,4 .
(1)求 a,b满足的关系式;
2 2
(2)若函数图象与 x轴无交点,求 a b 的取值范围.
23. (10 分)定义:圆心在三角形的一边上,与另一边相切,且经过三角形一个顶点(非切
点)的圆,称为这个三角形圆心所在边上的“伴随圆”.
(1)如图①,在 ABC中, C 90 ,AB 5,AC 3,则 BC边上的伴随圆的半径为________.
(2)如图②, ABC中 ACB 90 ,点 E在边 AB上, AE 2BE,D为 AC的中点,且
CED 90 .
①求证:△CED的外接圆是 ABC的 AC边上的伴随圆;
DE
② 的值为_________
CE
3
24.(12 分)如图,抛物线 = 2 + ( ≠ 0) 与 x 轴交于点 A,B,与 y 轴交于
2
点 (0, 2) , tan∠ = 1 .直线 = 1 交 于点 D,点 P 是直线 下方抛物线上一
2
动点,连接 PD.
(1)求此抛物线的解析式;
(2)如图 1,连接 ,求 △ 面积的最大值及此时点 P 的坐标;
(3)如图 2,连接 ,过点 P 作 ⊥ 于点 E,是否存在点 P使以 P,D,E 三点为顶点
的三角形与 △ 相似,若存在,直接写出点 P 的坐标;若不存在,请说明理由.
数学参考答案
一、选择题(每小题 3 分,共 30 分.在每小题给出的四个选项中,只有一项符合题目要求)
1 2 3 4 5 6 7 8 9 10
B B C A C A C B C D
二、填空题(每小题 4 分,共 24 分)
1 3
11. 30 12. 13.
3 2
14. 6或2 30 15. 20 16. 2 13 2
三、解答题(本大题有 7 题,共 66 分)
17.(6分)
2
解:原式= 2 2 2 1 3 .................................4分
2
= 2 2 .......................................................6分
18.(6分)
(1)50; 补全折线统计图如解图①.......................2分
(2)D 15所对应扇形圆心角的大小为 360°× =108°,
50
∴D所对应的扇形圆心角的大小为 108°;..........................4分
(3)画树状图如解图②,
共有 16种等可能的结果,小林和小峰选择相同主题的结果有 4种,
4 1
∴小林和小峰选择相同主题的概率为 = ...........................................6分
16 4
1
19.(8分)(每小题 4分)(1)如图,线段 AD 就是所求作的中线;
(2)如图:在5 5的正三角形的网格中,
∵MN∥AB∥FD,
∴∠AEC=∠FDC,
∵四边形 CMGN 为菱形,且边长为 5,
∴CG⊥MN,
∴CG⊥FD,
OG MG sin 60 3 5 3 5 ,
2 2
∴CG=2OG=5 3,
∵△GFD 为等边三角形,且边长为 2,
同理:HG= 3,
∴在 Rt△CDH 中,∠CHD=90 ,DH=1,CH=CG-HG=4 3,
2
2
∴DH2 CH2 CD2,即12 4 3 CD2 ,
∴CD 7,
∴ cos AEC cos FDC
DH 1
.
CH 7
20(每小题 4分,共 8分).
解:(1)过点A作 AH BC于点H .
∵ BAD 135 , BC //AD, C 90 ,
∴ ABC=45 ,CD AD.
设CD x,则 AH BH CD x ,
∴ AD HC 15 2x,
设储料场的面积为S,则 S x 15 2x 1 x 2,
2
S 3 2 75∴ x 5 .
2 2
∴当 x 5时,储料场的面积最大,最大面积为 37.5m2 .此时 AD 15 2 5 5.
故当 AD = DC = 5米, BC 10米时,所建储料场的面积最大,最大面积为 37.5m2 .
(2)小聪建议合理.理由如下:
135 AD
由题意得 15,
180
AD 20∴ .
S 1 20 150∴ 15 .
2
150
∵ 47.7 37.5,
∴小聪的建议是合理的.
21. (每小题 4分,共 8分)
(1)证明:∵OC 为半径,E 为 AD 中点.
∴OC⊥AD,AC=CD,
∴∠ABC=∠CAD;
(2)解:在 Rt△ABC 中,AB=5,AC=3,则 BC=4,
∴sin∠CBA= = ,
3
∴sin∠CAD= ,则 CE= ,
则 AE= = =ED,
∵cos∠CBA= ,则 cos∠CAD= ,
则 AF= = ,
∴EF=AF﹣AE= ﹣ = ,
则 FD=AD﹣AF= ﹣ = ,
∴EF:FD=9:7.
22. (每小题 4分,共 8分)
解:(1)∵二次函数 y ax2 bx c a 0 的图象经过点 A 1,1 和B 2,4 ,
a b c 1①
∴ ,
4a 2b c 4②
②-①得,3a 3b 3,即 a b 1,
∴b 1 a;
(2)∵函数图象与 x轴无交点,
b2∴ 4ac 0,即 1 a 2 4a 2 2a 0,∴ 1 a 1 9a 0,
1
解得 a 1,∵b 1 a,
9
1 2 1
∴ a2 b2 a2 1 a 2 a2 a2 2a 1 2a2 2a 1 2 a 2 , 2
1 1
∴当 a 时, a2 b2 的最小值为 ,当 a 1时, a2 b2 的最大值为 1,
2 2
1
∴ a2 b2 1.
2
日期:2020/9/20 22:45:06;用户:忘忧草;邮箱:987462668@qcom;学号: 12 3.(10分)(第 1 小题 3 分,第 2 小题①4 分,②3 分,)
(1)解:∵ C 90 , AB 5, BC 3,
4
∴ AC AB2 BC2 4,
∵ BC是圆的切线, BCA 90 ,
∴ AC为圆的直径.
∴ AC边上的伴随圆的半径为 2.
故答案为:2.
(2)证明:①证明:如图连接OE、OB,
∵△CED为直角三角形,
∴△CED的外接圆圆心 O 在CD中点上,
设 O的半径为 r,则DC 2r,OA 3r,
AD 2
∴ ,
AO 3
∵ EA= 2BE,
EA 2
∴ ,
AB 3
AD EA
∴ ,
AO AB
∴ PD∥OB,
∴ 1 2, 3= 4,
∵OE = OD,
∴ 3 2,
∴ 1 4,
OC OP
在 BCO和△BEO
中 1 4 ,
OB OB
∴ BCO≌ BEO,
∴ BEO BCO 90 ,
∴ AB是 O的切线.
∴△CED的外接圆是 ABC某一条边上的伴随圆;
②如图设圆 O 的半径为 r,
5
∵在Rt△OAE中,OA 3r,OE r,
∴ EA OA2 OE 2 2 2r,
∴ AB 3 2r,
∵在Rt△ABC中, AC 4r, AB 3 2r,
∴ BC AB2 AC2 2r
∵在Rt△OBC中,OC r, BC 2r,
∴OB OC 2 CB2 3r,
∴ cos 1 OC r 3 ,
OB 3r 3
∵ EDC 1,
∴ cos EDC 3 ,
3
∴DE CD cos CDE 2 3 r ,
3
2
∴CE CD2 DE2
2r 2 2 3 2 6 r r,
3 3
2 3
DE r
∴ 3
2
.
CE 2 6 2r
3
2
故答案为: .
2
24.(每小题 4 分,共 12 分)
解: ∵ (0, 2) ,
∴ = 2 ,
∵ 在 △ tan = = 2 = 1中, ∠ ,
2
∴ = 4 ,即 (4,0) ,
16 6 + = 0
将点 (4,0), (0, 2) 代入抛物线的解析式得: { = 2 ,
6
{ =
1
解得 2 ,
= 2
1 3
则此抛物线的解析式为 = 2 2 ;
2 2
(2)解:设直线 BC 的函数解析式为 = + ,
4 + = 0 = 1
将点 (4,0), (0, 2) 代入得: { = 2 ,解得 { 2 , = 2
1
则直线 BC 的函数解析式为 = 2 ,
2
当 = 1 1时, = × 1 2 = 3 3,即 (1, ) ,
2 2 2
则 = (1 0)2 + ( 3 + 2)2 = 5 ,
2 2
要使 △ 的面积最大,则需要点 P 到 CD 的距离最大,
设与直线 BC 平行的直线 ' 1的函数解析式为 = + ,则 (0, ), = 2 ,
2
如图,过点 C 作 ⊥ ' 于点 E,则 CE 为直线 BC 与直线 ' 间的距离,
在 △ 中, = 4, = 2 + 2 = 2 5 2 5,则 sin∠ = = ,
5
∵ // ' ,
∴ ∠ = ∠ ,
∴ sin∠ = sin∠ = 2 5 ,
5
在 △ 中, sin∠ = = = 2 5 ,
2 5
2 5
解得 = ( 2 ) ,
5
∴ 1 3越小,CE 越大,当直线 ' 要与抛物线 = 2 2 有交点,
2 2
1
即当直线 ' 与 = 2 3 2 有且只有一个交点时, 最小,此时的交点即为点 P,
2 2
7
= 1 2 3 2
联立 { 2 2 ,
= 1 +
2
1
整理得: 2 2 2 = 0 ,
2
则其根的判别式 = 4 4 × 1 ( 2 ) = 0 ,
2
解得 = 4 ,
2 5
则此时 = × ( 2 + 4) = 4 5 ,
5 5
△ 1 × 5 4 5面积的最大值为 × = 1 ,
2 2 5
将 = 4 1代入 2 2 2 = 0 得: 1= 2 2=2 ,
当 = 2 时, = 1 × 22 3 × 2 2 = 3 ,
2 2
∴△ 面积取得最大值时,点 P 的坐标为 (2, 3) ;
= 1 2 3(3)解:对于 2 ,
2 2
当 = 0 1 3时, 2 2 = 0 ,解得 = 1, = 4 ,
2 2
∴ ( 1,0) ,
∵ (4,0), (0, 2) ,
∴ = 4 + 1 = 5, = 12 + 22 = 5, = 22 + 42 = 2 5 ,
∴ 2 + 2 = 2 ,
∴△ 是直角三角形,且 ∠ = 90° ,
( , 1 2 3设点 P的坐标为 2) ,
2 2
∵ ⊥ 1,直线 BC 的函数解析式为 = 2 ,
2
∴ 设直线 PE 的函数解析式为 = 2 + ,
1
将 ( , 2 3 2) 1 3代入得: 2 + = 2 2 ,
2 2 2 2
解得 = 1 2 + 1 2 ,
2 2
1 1
则直线 PE 的函数解析式为 = 2 + 2 + 2 ,
2 2
= 2 + 1 2 + 1 2 = 1 2 + 1
联立 { 2 21 ,解得 {
5 5 ,
= 2 = 1 2 + 1 2
2 10 10
即 ( 1 2 + 1 , 1 2 + 1 2) ,
5 5 10 10
8
∴ 2 = ( 1 2 4 )2 + ( 2 2 + 8 )2 ,
5 5 5 5
2 = ( 1 2 + 1 1)2 + ( 1 2 + 1 1 )2 ,
5 5 10 10 2
由题意,分以下两种情况:
①当 △ △ 时,
= = 5 1则 = ,即 2 = 4 2 ,
2 5 2
3+ 13 17 229
解得 = 或 = ,
2 6
( 3+ 13 , 13 ) ( 17 229 17 10 229则此时 或 , ) ;
2 2 6 18
②当 △ △ 时,
= = 2 5则 = 2 ,即 2 = 4 2 ,
5
= 5解得 ,
2
5 21
则此时 ( , ) ;
2 8
3+ 13 13
综上,存在这样的点 P,此时点 P 的坐标为 ( , ) ( 17 229 , 17 10 229或 ) 或
2 2 6 18
( 5 , 21 ) .
2 8
9
一、选择题(共 10 小题,每题 3 分)
1.如图,四边形 ABCD内接于 O,若 C 130 ,则 BOD的度数为( )
A. 50 B. 100 C. 130 D. 150
2.已知 x, y, z 2 3 5 5x y满足 ,则 的值为( )
x y z z x y 2z
1 1 1
A.1 B. C. D.
3 3 2
3.如图 A、B、C在⊙O上,连接 OA、OB、OC,若∠BOC=3∠AOB,劣弧 AC
的度数是 120o,OC= 2 3.则图中阴影部分的面积是 ( )
A 1. 32 B. 2 3 C.3 2 3 D.4π-3 3
4. x 5 3设 ,则代数式 x(x 1)(x 2)(x 3)的值为( )
2
A、-1 B、1 C、0 D、2
5. 点O是 ABC的外心,也是△BCD的内心,若 A 70 ,则 BDC的度数是
( )
A. 80° B. 90° C. 100° D. 110°
6.如图 1,正方形 ABCD绕中心 O逆时针旋转 45°得到正方形 A B C D ,现将整个图形的外围
以 O为位似中心得到位似图形如图 2 1所示,位似比为 2 ,若整个图形的外围周长为 16,则图
中的阴影部分面积为( )
A.6 3 2 B. 4 2 2 C.2 2 D.8 4 2
ab
7.已知 AC⊥BC于 C,BC=a,CA=b,AB=c,下列选项中⊙O的半径为 的是( ).
a b
2
8.二次函数 y=ax +bx+c(a≠0)的大致图象如图所示,顶点坐标为(1,﹣4a),
点 A(4,y1)是该抛物线上一点,若点 D(x2,y2)是抛物线上任意一点,有下列结
论:
①4a﹣2b+c>0;
②若 y2>y1,则 x2>4;
③若 0≤x2≤4,则 0≤y2≤5a;
④若方程 a(x+1)(x﹣3)=﹣1 有两个实数根 x1和 x2,且 x1<x2,则﹣1<x1<x2<3.
其中正确结论的个数是( )
A.1 个 B.2个 C.3个 D.4 个
9.锐角三角形ABC的三边是a,b,c,它的外心到三边的距离分别为m,n,p,那么m:n:p
等于 ( )
1 1 1
A. : : ; B.a∶b∶c; C.cosA∶cosB∶cosC; D.sinA∶sinB∶sinC.
a b c
10.如图,点 O为正方形 ABCD的中心,以 BC的中点 H为圆心,HA为半径画弧交CB的延
长线于点 E.以 BE为边向上作正方形 BEFG,过点 A作 AK AE交CD于点 K,取 EK 的中点
M,连结MO.已知 AD 2 5 2,则OM 的长为( )
A 5 1 B 10 2. . C.3 D. 2 2
2
二.填空题(共 6 小题,每题 4 分,共 24 分)
11.如图,是某商店售卖的花架,其中 AD∥BE∥CF,DE 24cm,EF 40cm,
BC 50cm,则 AB长为_________cm.
12.把一根长度为 6 的铁丝截成 3 段,若三段的长度均为正整数,则能构成三角形的概率为
________.
13.因为 cos60° 1= ,cos 240° 1=- ,所以 cos 240°=cos(180°+60°)=-cos 60°;由
2 2
此猜想、推理知:当α为锐角时有 cos (180°+α)=-cos α,则:cos 210°=
14.如图,在 △ 中,∠ = 90°,E为 边上一点,以 为直径的
半圆O与 相切于点D,连接 , = 3, = 3 5.P是 边上
的动点,当△ 为等腰三角形时, 的长为 .
15.图 1是一款由若干条吊链等间距悬挂而成的挂帘,吊链顶端悬挂在水
平横梁上,自然下垂时底部呈圆弧形,其中最长吊链为95cm,最短吊链为
45cm,挂满后呈轴对称分布.图 2是其示意图,其中最长两条吊链 AC与BD
之间的距离 AB为114cm.若吊链数量为偶数,记对称轴右侧最短挂链的底端为点 F,当 C,F,
B三点在同一条直线上时,吊链的数量为 .
16. 如图,已知正方形 ABCD的边长为 4,点 E是正方形内部一点,连接 EA,
EB满足 EAB EBC ,点 P是 BC边上一动点,连结 PD, PE.则
PD PE长度的最小值为
三、(共 8 小题,计 66 分)
1 1
17.(6分)计算: 8 2sin 45 (2 ) 0
3
18.(6分)2023年 5月 30日上午,神舟十六号载人飞船成功发射,举国振奋.为了使同学们
进一步了解中国航天科技的快速发展,余姚某中学九(1)班团支部组织了一场手抄报比赛.要
求该班每位同学从 A:“北斗”,B:“5G时代”,C:“东风快递”,D:“智轨快运”四
个主题中任选一个自己喜爱的主题.比赛结束后,该班团支部统计了同学们所选主题的频数,
绘制成如图两种不完整的统计图,请根据统计图中的信息解答下列问题.
九(1)班学生喜爱 九(1)班学生喜爱
的主题折线图 的主题扇形图
图① 图②
(1)九(1)班共有________名学生;并补全图①折线统计图;
(2)请阅读图②,求出 D所对应的扇形圆心角的度数;
(3)若小余和小姚分别从 A,B,C,D四个主题中任选一个主题,请用列表或画树状图的方法
求出他们选择相同主题的概率.
19.(8分)如图,在5 5的正三角形的网格中, ABC的三个顶点都在格点上.请按要求画图
和计算:①仅用无刻度直尺;②保留作图痕迹.
(1)在图 1中,画出 ABC的BC边上的中线 AD.
(2)在图 2中,直接写出 cos AEC的值.
20. (8分)现有成 135°角且足够长的墙角和可建总长为 15m围墙的建筑用料来修建储料场.
(1)如图 1,修建成四边形 ABCD的一个储料场,使BC //AD, C 90 .新建围墙为 BCD.怎
样修建围墙才能使储料场的面积最大?最大面积是多少?
(2)爱动脑筋的小聪建议:把新建的围墙建成如图 2所示的以 A为圆心的圆弧 BD,这样修
建的储料场面积会更大.聪明的你认为小聪的建议合理吗?请说明理由.
21.(8分)如图,△ABC 内接于⊙O,AB 为⊙O 的直径,AB=5,AC=3.连接 OC,
弦 AD 分别交 OC,BC 于点 E,F,其中点 E是 AD 的中点.
(1)求证:∠CAD=∠CBA.
(2)求 EF:FD 的值.
22.(8 2分)已知二次函数 y ax bx c a 0 的图象经过点 A 1,1 和 B 2,4 .
(1)求 a,b满足的关系式;
2 2
(2)若函数图象与 x轴无交点,求 a b 的取值范围.
23. (10 分)定义:圆心在三角形的一边上,与另一边相切,且经过三角形一个顶点(非切
点)的圆,称为这个三角形圆心所在边上的“伴随圆”.
(1)如图①,在 ABC中, C 90 ,AB 5,AC 3,则 BC边上的伴随圆的半径为________.
(2)如图②, ABC中 ACB 90 ,点 E在边 AB上, AE 2BE,D为 AC的中点,且
CED 90 .
①求证:△CED的外接圆是 ABC的 AC边上的伴随圆;
DE
② 的值为_________
CE
3
24.(12 分)如图,抛物线 = 2 + ( ≠ 0) 与 x 轴交于点 A,B,与 y 轴交于
2
点 (0, 2) , tan∠ = 1 .直线 = 1 交 于点 D,点 P 是直线 下方抛物线上一
2
动点,连接 PD.
(1)求此抛物线的解析式;
(2)如图 1,连接 ,求 △ 面积的最大值及此时点 P 的坐标;
(3)如图 2,连接 ,过点 P 作 ⊥ 于点 E,是否存在点 P使以 P,D,E 三点为顶点
的三角形与 △ 相似,若存在,直接写出点 P 的坐标;若不存在,请说明理由.
数学参考答案
一、选择题(每小题 3 分,共 30 分.在每小题给出的四个选项中,只有一项符合题目要求)
1 2 3 4 5 6 7 8 9 10
B B C A C A C B C D
二、填空题(每小题 4 分,共 24 分)
1 3
11. 30 12. 13.
3 2
14. 6或2 30 15. 20 16. 2 13 2
三、解答题(本大题有 7 题,共 66 分)
17.(6分)
2
解:原式= 2 2 2 1 3 .................................4分
2
= 2 2 .......................................................6分
18.(6分)
(1)50; 补全折线统计图如解图①.......................2分
(2)D 15所对应扇形圆心角的大小为 360°× =108°,
50
∴D所对应的扇形圆心角的大小为 108°;..........................4分
(3)画树状图如解图②,
共有 16种等可能的结果,小林和小峰选择相同主题的结果有 4种,
4 1
∴小林和小峰选择相同主题的概率为 = ...........................................6分
16 4
1
19.(8分)(每小题 4分)(1)如图,线段 AD 就是所求作的中线;
(2)如图:在5 5的正三角形的网格中,
∵MN∥AB∥FD,
∴∠AEC=∠FDC,
∵四边形 CMGN 为菱形,且边长为 5,
∴CG⊥MN,
∴CG⊥FD,
OG MG sin 60 3 5 3 5 ,
2 2
∴CG=2OG=5 3,
∵△GFD 为等边三角形,且边长为 2,
同理:HG= 3,
∴在 Rt△CDH 中,∠CHD=90 ,DH=1,CH=CG-HG=4 3,
2
2
∴DH2 CH2 CD2,即12 4 3 CD2 ,
∴CD 7,
∴ cos AEC cos FDC
DH 1
.
CH 7
20(每小题 4分,共 8分).
解:(1)过点A作 AH BC于点H .
∵ BAD 135 , BC //AD, C 90 ,
∴ ABC=45 ,CD AD.
设CD x,则 AH BH CD x ,
∴ AD HC 15 2x,
设储料场的面积为S,则 S x 15 2x 1 x 2,
2
S 3 2 75∴ x 5 .
2 2
∴当 x 5时,储料场的面积最大,最大面积为 37.5m2 .此时 AD 15 2 5 5.
故当 AD = DC = 5米, BC 10米时,所建储料场的面积最大,最大面积为 37.5m2 .
(2)小聪建议合理.理由如下:
135 AD
由题意得 15,
180
AD 20∴ .
S 1 20 150∴ 15 .
2
150
∵ 47.7 37.5,
∴小聪的建议是合理的.
21. (每小题 4分,共 8分)
(1)证明:∵OC 为半径,E 为 AD 中点.
∴OC⊥AD,AC=CD,
∴∠ABC=∠CAD;
(2)解:在 Rt△ABC 中,AB=5,AC=3,则 BC=4,
∴sin∠CBA= = ,
3
∴sin∠CAD= ,则 CE= ,
则 AE= = =ED,
∵cos∠CBA= ,则 cos∠CAD= ,
则 AF= = ,
∴EF=AF﹣AE= ﹣ = ,
则 FD=AD﹣AF= ﹣ = ,
∴EF:FD=9:7.
22. (每小题 4分,共 8分)
解:(1)∵二次函数 y ax2 bx c a 0 的图象经过点 A 1,1 和B 2,4 ,
a b c 1①
∴ ,
4a 2b c 4②
②-①得,3a 3b 3,即 a b 1,
∴b 1 a;
(2)∵函数图象与 x轴无交点,
b2∴ 4ac 0,即 1 a 2 4a 2 2a 0,∴ 1 a 1 9a 0,
1
解得 a 1,∵b 1 a,
9
1 2 1
∴ a2 b2 a2 1 a 2 a2 a2 2a 1 2a2 2a 1 2 a 2 , 2
1 1
∴当 a 时, a2 b2 的最小值为 ,当 a 1时, a2 b2 的最大值为 1,
2 2
1
∴ a2 b2 1.
2
日期:2020/9/20 22:45:06;用户:忘忧草;邮箱:987462668@qcom;学号: 12 3.(10分)(第 1 小题 3 分,第 2 小题①4 分,②3 分,)
(1)解:∵ C 90 , AB 5, BC 3,
4
∴ AC AB2 BC2 4,
∵ BC是圆的切线, BCA 90 ,
∴ AC为圆的直径.
∴ AC边上的伴随圆的半径为 2.
故答案为:2.
(2)证明:①证明:如图连接OE、OB,
∵△CED为直角三角形,
∴△CED的外接圆圆心 O 在CD中点上,
设 O的半径为 r,则DC 2r,OA 3r,
AD 2
∴ ,
AO 3
∵ EA= 2BE,
EA 2
∴ ,
AB 3
AD EA
∴ ,
AO AB
∴ PD∥OB,
∴ 1 2, 3= 4,
∵OE = OD,
∴ 3 2,
∴ 1 4,
OC OP
在 BCO和△BEO
中 1 4 ,
OB OB
∴ BCO≌ BEO,
∴ BEO BCO 90 ,
∴ AB是 O的切线.
∴△CED的外接圆是 ABC某一条边上的伴随圆;
②如图设圆 O 的半径为 r,
5
∵在Rt△OAE中,OA 3r,OE r,
∴ EA OA2 OE 2 2 2r,
∴ AB 3 2r,
∵在Rt△ABC中, AC 4r, AB 3 2r,
∴ BC AB2 AC2 2r
∵在Rt△OBC中,OC r, BC 2r,
∴OB OC 2 CB2 3r,
∴ cos 1 OC r 3 ,
OB 3r 3
∵ EDC 1,
∴ cos EDC 3 ,
3
∴DE CD cos CDE 2 3 r ,
3
2
∴CE CD2 DE2
2r 2 2 3 2 6 r r,
3 3
2 3
DE r
∴ 3
2
.
CE 2 6 2r
3
2
故答案为: .
2
24.(每小题 4 分,共 12 分)
解: ∵ (0, 2) ,
∴ = 2 ,
∵ 在 △ tan = = 2 = 1中, ∠ ,
2
∴ = 4 ,即 (4,0) ,
16 6 + = 0
将点 (4,0), (0, 2) 代入抛物线的解析式得: { = 2 ,
6
{ =
1
解得 2 ,
= 2
1 3
则此抛物线的解析式为 = 2 2 ;
2 2
(2)解:设直线 BC 的函数解析式为 = + ,
4 + = 0 = 1
将点 (4,0), (0, 2) 代入得: { = 2 ,解得 { 2 , = 2
1
则直线 BC 的函数解析式为 = 2 ,
2
当 = 1 1时, = × 1 2 = 3 3,即 (1, ) ,
2 2 2
则 = (1 0)2 + ( 3 + 2)2 = 5 ,
2 2
要使 △ 的面积最大,则需要点 P 到 CD 的距离最大,
设与直线 BC 平行的直线 ' 1的函数解析式为 = + ,则 (0, ), = 2 ,
2
如图,过点 C 作 ⊥ ' 于点 E,则 CE 为直线 BC 与直线 ' 间的距离,
在 △ 中, = 4, = 2 + 2 = 2 5 2 5,则 sin∠ = = ,
5
∵ // ' ,
∴ ∠ = ∠ ,
∴ sin∠ = sin∠ = 2 5 ,
5
在 △ 中, sin∠ = = = 2 5 ,
2 5
2 5
解得 = ( 2 ) ,
5
∴ 1 3越小,CE 越大,当直线 ' 要与抛物线 = 2 2 有交点,
2 2
1
即当直线 ' 与 = 2 3 2 有且只有一个交点时, 最小,此时的交点即为点 P,
2 2
7
= 1 2 3 2
联立 { 2 2 ,
= 1 +
2
1
整理得: 2 2 2 = 0 ,
2
则其根的判别式 = 4 4 × 1 ( 2 ) = 0 ,
2
解得 = 4 ,
2 5
则此时 = × ( 2 + 4) = 4 5 ,
5 5
△ 1 × 5 4 5面积的最大值为 × = 1 ,
2 2 5
将 = 4 1代入 2 2 2 = 0 得: 1= 2 2=2 ,
当 = 2 时, = 1 × 22 3 × 2 2 = 3 ,
2 2
∴△ 面积取得最大值时,点 P 的坐标为 (2, 3) ;
= 1 2 3(3)解:对于 2 ,
2 2
当 = 0 1 3时, 2 2 = 0 ,解得 = 1, = 4 ,
2 2
∴ ( 1,0) ,
∵ (4,0), (0, 2) ,
∴ = 4 + 1 = 5, = 12 + 22 = 5, = 22 + 42 = 2 5 ,
∴ 2 + 2 = 2 ,
∴△ 是直角三角形,且 ∠ = 90° ,
( , 1 2 3设点 P的坐标为 2) ,
2 2
∵ ⊥ 1,直线 BC 的函数解析式为 = 2 ,
2
∴ 设直线 PE 的函数解析式为 = 2 + ,
1
将 ( , 2 3 2) 1 3代入得: 2 + = 2 2 ,
2 2 2 2
解得 = 1 2 + 1 2 ,
2 2
1 1
则直线 PE 的函数解析式为 = 2 + 2 + 2 ,
2 2
= 2 + 1 2 + 1 2 = 1 2 + 1
联立 { 2 21 ,解得 {
5 5 ,
= 2 = 1 2 + 1 2
2 10 10
即 ( 1 2 + 1 , 1 2 + 1 2) ,
5 5 10 10
8
∴ 2 = ( 1 2 4 )2 + ( 2 2 + 8 )2 ,
5 5 5 5
2 = ( 1 2 + 1 1)2 + ( 1 2 + 1 1 )2 ,
5 5 10 10 2
由题意,分以下两种情况:
①当 △ △ 时,
= = 5 1则 = ,即 2 = 4 2 ,
2 5 2
3+ 13 17 229
解得 = 或 = ,
2 6
( 3+ 13 , 13 ) ( 17 229 17 10 229则此时 或 , ) ;
2 2 6 18
②当 △ △ 时,
= = 2 5则 = 2 ,即 2 = 4 2 ,
5
= 5解得 ,
2
5 21
则此时 ( , ) ;
2 8
3+ 13 13
综上,存在这样的点 P,此时点 P 的坐标为 ( , ) ( 17 229 , 17 10 229或 ) 或
2 2 6 18
( 5 , 21 ) .
2 8
9
同课章节目录
