第五单元《三平行四边形和梯形》同步练习2023年秋四年级上册数学人教版(含解析)
文档属性
| 名称 | 第五单元《三平行四边形和梯形》同步练习2023年秋四年级上册数学人教版(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 110.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-09 13:31:44 | ||
图片预览




文档简介
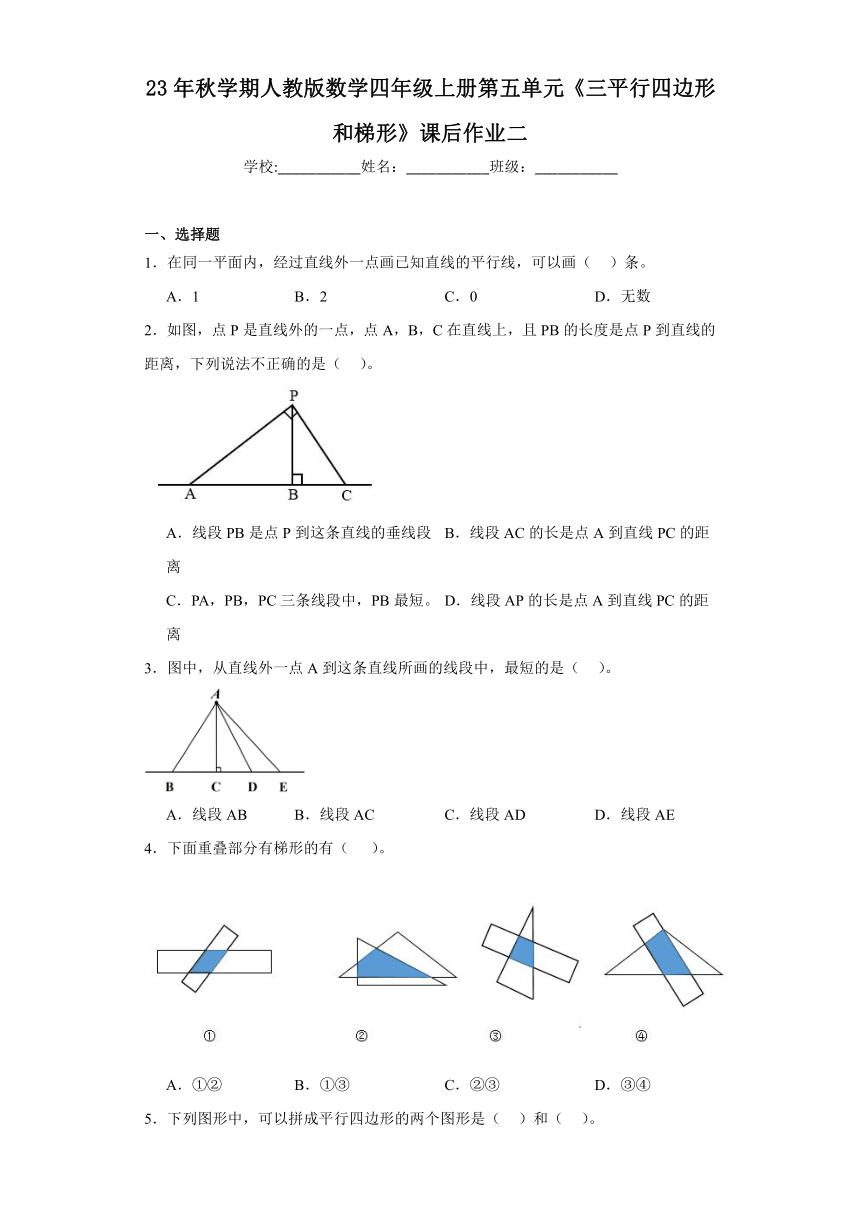
23年秋学期人教版数学四年级上册第五单元《三平行四边形和梯形》课后作业二
学校:___________姓名:___________班级:___________
一、选择题
1.在同一平面内,经过直线外一点画已知直线的平行线,可以画( )条。
A.1 B.2 C.0 D.无数
2.如图,点P是直线外的一点,点A,B,C在直线上,且PB的长度是点P到直线的距离,下列说法不正确的是( )。
A.线段PB是点P到这条直线的垂线段 B.线段AC的长是点A到直线PC的距离
C.PA,PB,PC三条线段中,PB最短。 D.线段AP的长是点A到直线PC的距离
3.图中,从直线外一点A到这条直线所画的线段中,最短的是( )。
A.线段AB B.线段AC C.线段AD D.线段AE
4.下面重叠部分有梯形的有( )。
A.①② B.①③ C.②③ D.③④
5.下列图形中,可以拼成平行四边形的两个图形是( )和( )。
A.、 B.、
C.、 D.、
二、填空题
6.一个等腰梯形的周长是48厘米,上底和下底分别是8厘米和10厘米,每条腰长( )厘米。
7.平行四边形和梯形都有( )条高,如图的梯形中,高为( )厘米。
8.把一个长方形拉成一个平行四边形,平行四边形的高( )长方形的宽(填“小于”“大于”或“等于”)。这个平行四边形的( )不变。
9.人们利用平行四边形( )的特性,制作了伸缩门。
10.如图,与直线b垂直的直线有( )条,与直线d平行的是直线( )。
三、判断题
11.同一平面内两条直线不是平行就是垂直。( )
12.一个长方形中有两组互相平行的线段。( )
13.当两条直线相交成180°角时,这两条直线互相垂直。( )
14.只有一组对边平行且有一个角是直角的四边形叫作直角梯形。( )
15.在下面两条平行线之间有一个正方形ABCD和一个平行四边形EFGH,它们的周长相比,平行四边形EFGH的周长比正方形ABCD的周长长。( )
四、解答题
16.育才小学有一个梯形的花坛,花坛的上底长4米,下底长6米,两腰各长5米。如果在花坛的四周围上护栏,护栏长多少米?
17.平行四边形相邻的两条边分别是2厘米和3厘米,用4个这样的平行四边形拼成更大的平行四边形,周长最长是多少?最短是多少?
18.如果天天、典典、龙龙三人跑得一样快,他们同时出发,谁最先抢到足球?画一画,并说明你判断的理由。
参考答案:
1.A
【详解】在同一平面内,经过直线外一点有且只有一条直线与已知直线平行,如下图:
故答案为:A
2.B
【分析】从直线外一点到这条直线所画的垂直线段最短,它的长度叫作点到直线的距离;依此判断并选择即可。
【详解】A.线段PB是点P到这条直线的垂线段,即原说法正确。
B.线段AC的长=线段AB的长度+线段BC的长度,即原说法不正确。
C.PA,PB,PC三条线段中,PB最短,即原说法正确。
D.线段AP的长是点A到直线PC的距离,即原说法正确。
故答案为:B
【点睛】此题考查的是点到直线的距离,应熟练掌握垂直的特点。
3.B
【分析】从直线外一点向直线所作的所有线段中,垂线段最短,据此解答即可。
【详解】因为线段AC与这条直线互相垂直,所以从直线外一点A到这条直线所画的线段中,最短的是线段AC。
故答案为:B
4.D
【分析】图中每个图形都是用长方形和三角形,或者长方形和长方形重叠形成的。长方形的对边平行且相等,只有一组对边平行的四边形是梯形,两组对边分别平行且相等的四边形是平行四边形。
【详解】A.图形①的重叠部分的四边形的两组对边分别平行且相等,是平行四边形;图形②的重叠部分的四边形没有平行的对边。
B.图形①的重叠部分的四边形的两组对边分别平行且相等,是平行四边形;图形③的重叠部分的四边形只有一组对边平行,是梯形。
C.图形②的重叠部分的四边形没有平行的对边;图形③的重叠部分的四边形只有一组对边平行,是梯形。
D.图形③的重叠部分的四边形只有一组对边平行,是梯形,图形④的重叠部分的四边形只有一组对边平行,是梯形。
重叠部分有梯形的有③④。
故答案为:D
5.A
【分析】平行四边形对边平行且相等,对角相等,再根据两个完全相同的梯形可以拼成一个平行四边形,进行解答即可。
【详解】根据分析可知,可以拼成平行四边形的两个图形是和。
故答案为:A
【点睛】本题主要考查图形的拼组,关键是培养学生的动手操作能力和想象能力。
6.15
【分析】因为梯形的周长=两腰长度+上底+下底,又根据等腰梯形的特点,两腰相等,所以一条腰的长度=(周长-上底-下底)÷2,代入数据计算即可。
【详解】(48-8-10)÷2
=(40-10)÷2
=30÷2
=15(厘米)
一个等腰梯形的周长是48厘米,上底和下底分别是8厘米和10厘米,每条腰长15厘米。
7. 无数 4
【分析】根据平行四边形、梯形的特征可知:平行四边形和梯形都有无数条高,上下底之间的距离就是平行四边形和梯形的高;据此解答。
【详解】根据分析:平行四边形和梯形都有无数条高,如图的梯形中,高为4厘米。
【点睛】本题考查了平行四边形及梯形的特征。
8. 小于 底
【分析】把一个长方形拉成一个平行四边形,在拉的过程中长方形的长变成平行四边形的底,长方形的宽变成平行四边形的斜边,在作平行四边形的高时原来长方形的宽变成直角三角形的斜边,在直角三角形中斜边最长。据此解答即可。
【详解】把一个长方形拉成一个平行四边形,平行四边形的高小于长方形的宽。这个平行四边形的底不变。如图:
9.易变形
【分析】由平行四边形的特性可知,平行四边形具有不稳定性,所以容易变形,制作伸缩门运用了平行四边形易变形的特性,据此解答即可。
【详解】人们利用平行四边形易变形的特性,制作了伸缩门。
10. 2 a
【分析】观察上图可知,直线a、直线d与直线b互相垂直,同一平面内,垂直于同一直线的两条直线互相平行,所以直线a和直线d互相平行,据此即可解答。
【详解】根据分析可知,与直线b垂直的直线有2条,与直线d平行的是直线a。
11.×
【分析】同一平面内的两条直线的位置关系只有两种:①不相交;②相交;
平行:在同一个平面内不相交的两条直线叫做平行线,也可以说这两条直线互相平行;
垂直:两条直线相交成直角,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,这两条直线的交点叫做垂足;据此解答。
【详解】同一平面内两条直线的位置关系只有两种,即平行和相交,垂直只是相交中的一种特殊情况;所以原题说法错误。
故答案为:×
12.√
【详解】同一平面内不相交的两条直线互相平行。两组对边分别平行、四个角都是直角的四边形叫做长方形。长方形的特征是:两组对边平行且相等,两条对角线相等且互相平分,有2条对称轴,长方形是特殊的平行四边形。
所以一个长方形中有两组互相平行的线段说法正确。
故答案为:√
13.×
【分析】根据垂直的性质可知,当两条直线相交成90°时,这两条直线互相垂直;据此解答。
【详解】由分析可知,当两条直线相交成90°(直角)时,这两条直线互相垂直;而当两条直线相交成180°时,两条直线重合,不能形成直角,所以原题干说法错误。
故答案为:×
14.√
【分析】只有一组对边平行的四边形叫做梯形,一腰垂直于底的梯形叫直角梯形;据此即可解答。
【详解】四边形只有一组对边平行,说明这个四边形是梯形,有一个角是直角,说明有一条腰垂直于底,根据直角梯形的定义可知,这个四边形是直角梯形,原说法正确。
故答案为:√
【点睛】本题主要考查学生对梯形的定义及分类知识的掌握和灵活运用。
15.√
【分析】一组平行线中垂直线段最短,正方形ABCD和平行四边形EFGH上、下两边相等,左、右两边平行四边形更长,所以平行四边形EFGH的周长长。
【详解】如下图所示:
平行四边形EFGH的两条边的边长相等,长度为3cm,另外两条边的长度大于3cm,而正方形ABCD的四条边的长度都为3cm,所以平行四边形EFGH的周长比正方形ABCD的周长长,故原题说法正确。
故答案为:√
【点睛】本题考查了正方形、平行四边形的特征以及垂线段的知识,结合题意分析解答即可。
16.20米
【分析】由题意可知,梯形花坛的上底长4米,下底长6米,两腰各长5米,四周围上护栏,要求护栏的长度。根据等腰梯形的周长=上底+下底+2×腰,代入数据计算即可。
【详解】由题意得:
4+6+2×5
=4+6+10
=10+10
=20(米)
答:护栏长20米。
17.28厘米;20厘米
【分析】要想拼成的平行四边形的周长最长,应将4个平行四边形的短边拼接起来,拼成一排,此时大平行四边形的一条边是(4×3)厘米,邻边是2厘米,周长是(4×3+2)×2厘米。
要想拼成的平行四边形的周长最短,应将4个平行四边形拼成2行2列,每行的2个平行四边形的短边相接,每列的2个平行四边形的长边相接,此时大平行四边形的一条边是(3×2)厘米,邻边是(2×2)厘米,周长是(3×2+2×2)×2厘米。
【详解】(4×3+2)×2
=(12+2)×2
=14×2
=28(厘米)
(3×2+2×2)×2
=(6+4)×2
=10×2
=20(厘米)
答:周长最长是28厘米,最短是20厘米。
18.典典;图见详解;从直线外一点到这条直线的线段中,垂直线段最短;天天、典典、龙龙三人在一条直线上,从足球到这条直线的距离中,典典到足球的距离就是垂线段,距离最短。
【分析】三人跑得一样快,说明速度相同,谁离足球的路程近,谁先抢到。过一点有且只有一条直线与已知直线垂直。从直线外一点到这条直线的线段中,垂直线段最短,这条垂直线段的长度叫做点到直线的距离。
【详解】
典典最先抢到足球,理由:从直线外一点到这条直线的线段中,垂直线段最短;天天、典典、龙龙三人在一条直线上,从足球到这条直线的距离中,典典到足球的距离就是垂线段,距离最短。
【点睛】此题应根据垂线段的性质进行解答。从直线外一点向已知直线画垂直线段和斜线,垂线段最短。
学校:___________姓名:___________班级:___________
一、选择题
1.在同一平面内,经过直线外一点画已知直线的平行线,可以画( )条。
A.1 B.2 C.0 D.无数
2.如图,点P是直线外的一点,点A,B,C在直线上,且PB的长度是点P到直线的距离,下列说法不正确的是( )。
A.线段PB是点P到这条直线的垂线段 B.线段AC的长是点A到直线PC的距离
C.PA,PB,PC三条线段中,PB最短。 D.线段AP的长是点A到直线PC的距离
3.图中,从直线外一点A到这条直线所画的线段中,最短的是( )。
A.线段AB B.线段AC C.线段AD D.线段AE
4.下面重叠部分有梯形的有( )。
A.①② B.①③ C.②③ D.③④
5.下列图形中,可以拼成平行四边形的两个图形是( )和( )。
A.、 B.、
C.、 D.、
二、填空题
6.一个等腰梯形的周长是48厘米,上底和下底分别是8厘米和10厘米,每条腰长( )厘米。
7.平行四边形和梯形都有( )条高,如图的梯形中,高为( )厘米。
8.把一个长方形拉成一个平行四边形,平行四边形的高( )长方形的宽(填“小于”“大于”或“等于”)。这个平行四边形的( )不变。
9.人们利用平行四边形( )的特性,制作了伸缩门。
10.如图,与直线b垂直的直线有( )条,与直线d平行的是直线( )。
三、判断题
11.同一平面内两条直线不是平行就是垂直。( )
12.一个长方形中有两组互相平行的线段。( )
13.当两条直线相交成180°角时,这两条直线互相垂直。( )
14.只有一组对边平行且有一个角是直角的四边形叫作直角梯形。( )
15.在下面两条平行线之间有一个正方形ABCD和一个平行四边形EFGH,它们的周长相比,平行四边形EFGH的周长比正方形ABCD的周长长。( )
四、解答题
16.育才小学有一个梯形的花坛,花坛的上底长4米,下底长6米,两腰各长5米。如果在花坛的四周围上护栏,护栏长多少米?
17.平行四边形相邻的两条边分别是2厘米和3厘米,用4个这样的平行四边形拼成更大的平行四边形,周长最长是多少?最短是多少?
18.如果天天、典典、龙龙三人跑得一样快,他们同时出发,谁最先抢到足球?画一画,并说明你判断的理由。
参考答案:
1.A
【详解】在同一平面内,经过直线外一点有且只有一条直线与已知直线平行,如下图:
故答案为:A
2.B
【分析】从直线外一点到这条直线所画的垂直线段最短,它的长度叫作点到直线的距离;依此判断并选择即可。
【详解】A.线段PB是点P到这条直线的垂线段,即原说法正确。
B.线段AC的长=线段AB的长度+线段BC的长度,即原说法不正确。
C.PA,PB,PC三条线段中,PB最短,即原说法正确。
D.线段AP的长是点A到直线PC的距离,即原说法正确。
故答案为:B
【点睛】此题考查的是点到直线的距离,应熟练掌握垂直的特点。
3.B
【分析】从直线外一点向直线所作的所有线段中,垂线段最短,据此解答即可。
【详解】因为线段AC与这条直线互相垂直,所以从直线外一点A到这条直线所画的线段中,最短的是线段AC。
故答案为:B
4.D
【分析】图中每个图形都是用长方形和三角形,或者长方形和长方形重叠形成的。长方形的对边平行且相等,只有一组对边平行的四边形是梯形,两组对边分别平行且相等的四边形是平行四边形。
【详解】A.图形①的重叠部分的四边形的两组对边分别平行且相等,是平行四边形;图形②的重叠部分的四边形没有平行的对边。
B.图形①的重叠部分的四边形的两组对边分别平行且相等,是平行四边形;图形③的重叠部分的四边形只有一组对边平行,是梯形。
C.图形②的重叠部分的四边形没有平行的对边;图形③的重叠部分的四边形只有一组对边平行,是梯形。
D.图形③的重叠部分的四边形只有一组对边平行,是梯形,图形④的重叠部分的四边形只有一组对边平行,是梯形。
重叠部分有梯形的有③④。
故答案为:D
5.A
【分析】平行四边形对边平行且相等,对角相等,再根据两个完全相同的梯形可以拼成一个平行四边形,进行解答即可。
【详解】根据分析可知,可以拼成平行四边形的两个图形是和。
故答案为:A
【点睛】本题主要考查图形的拼组,关键是培养学生的动手操作能力和想象能力。
6.15
【分析】因为梯形的周长=两腰长度+上底+下底,又根据等腰梯形的特点,两腰相等,所以一条腰的长度=(周长-上底-下底)÷2,代入数据计算即可。
【详解】(48-8-10)÷2
=(40-10)÷2
=30÷2
=15(厘米)
一个等腰梯形的周长是48厘米,上底和下底分别是8厘米和10厘米,每条腰长15厘米。
7. 无数 4
【分析】根据平行四边形、梯形的特征可知:平行四边形和梯形都有无数条高,上下底之间的距离就是平行四边形和梯形的高;据此解答。
【详解】根据分析:平行四边形和梯形都有无数条高,如图的梯形中,高为4厘米。
【点睛】本题考查了平行四边形及梯形的特征。
8. 小于 底
【分析】把一个长方形拉成一个平行四边形,在拉的过程中长方形的长变成平行四边形的底,长方形的宽变成平行四边形的斜边,在作平行四边形的高时原来长方形的宽变成直角三角形的斜边,在直角三角形中斜边最长。据此解答即可。
【详解】把一个长方形拉成一个平行四边形,平行四边形的高小于长方形的宽。这个平行四边形的底不变。如图:
9.易变形
【分析】由平行四边形的特性可知,平行四边形具有不稳定性,所以容易变形,制作伸缩门运用了平行四边形易变形的特性,据此解答即可。
【详解】人们利用平行四边形易变形的特性,制作了伸缩门。
10. 2 a
【分析】观察上图可知,直线a、直线d与直线b互相垂直,同一平面内,垂直于同一直线的两条直线互相平行,所以直线a和直线d互相平行,据此即可解答。
【详解】根据分析可知,与直线b垂直的直线有2条,与直线d平行的是直线a。
11.×
【分析】同一平面内的两条直线的位置关系只有两种:①不相交;②相交;
平行:在同一个平面内不相交的两条直线叫做平行线,也可以说这两条直线互相平行;
垂直:两条直线相交成直角,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,这两条直线的交点叫做垂足;据此解答。
【详解】同一平面内两条直线的位置关系只有两种,即平行和相交,垂直只是相交中的一种特殊情况;所以原题说法错误。
故答案为:×
12.√
【详解】同一平面内不相交的两条直线互相平行。两组对边分别平行、四个角都是直角的四边形叫做长方形。长方形的特征是:两组对边平行且相等,两条对角线相等且互相平分,有2条对称轴,长方形是特殊的平行四边形。
所以一个长方形中有两组互相平行的线段说法正确。
故答案为:√
13.×
【分析】根据垂直的性质可知,当两条直线相交成90°时,这两条直线互相垂直;据此解答。
【详解】由分析可知,当两条直线相交成90°(直角)时,这两条直线互相垂直;而当两条直线相交成180°时,两条直线重合,不能形成直角,所以原题干说法错误。
故答案为:×
14.√
【分析】只有一组对边平行的四边形叫做梯形,一腰垂直于底的梯形叫直角梯形;据此即可解答。
【详解】四边形只有一组对边平行,说明这个四边形是梯形,有一个角是直角,说明有一条腰垂直于底,根据直角梯形的定义可知,这个四边形是直角梯形,原说法正确。
故答案为:√
【点睛】本题主要考查学生对梯形的定义及分类知识的掌握和灵活运用。
15.√
【分析】一组平行线中垂直线段最短,正方形ABCD和平行四边形EFGH上、下两边相等,左、右两边平行四边形更长,所以平行四边形EFGH的周长长。
【详解】如下图所示:
平行四边形EFGH的两条边的边长相等,长度为3cm,另外两条边的长度大于3cm,而正方形ABCD的四条边的长度都为3cm,所以平行四边形EFGH的周长比正方形ABCD的周长长,故原题说法正确。
故答案为:√
【点睛】本题考查了正方形、平行四边形的特征以及垂线段的知识,结合题意分析解答即可。
16.20米
【分析】由题意可知,梯形花坛的上底长4米,下底长6米,两腰各长5米,四周围上护栏,要求护栏的长度。根据等腰梯形的周长=上底+下底+2×腰,代入数据计算即可。
【详解】由题意得:
4+6+2×5
=4+6+10
=10+10
=20(米)
答:护栏长20米。
17.28厘米;20厘米
【分析】要想拼成的平行四边形的周长最长,应将4个平行四边形的短边拼接起来,拼成一排,此时大平行四边形的一条边是(4×3)厘米,邻边是2厘米,周长是(4×3+2)×2厘米。
要想拼成的平行四边形的周长最短,应将4个平行四边形拼成2行2列,每行的2个平行四边形的短边相接,每列的2个平行四边形的长边相接,此时大平行四边形的一条边是(3×2)厘米,邻边是(2×2)厘米,周长是(3×2+2×2)×2厘米。
【详解】(4×3+2)×2
=(12+2)×2
=14×2
=28(厘米)
(3×2+2×2)×2
=(6+4)×2
=10×2
=20(厘米)
答:周长最长是28厘米,最短是20厘米。
18.典典;图见详解;从直线外一点到这条直线的线段中,垂直线段最短;天天、典典、龙龙三人在一条直线上,从足球到这条直线的距离中,典典到足球的距离就是垂线段,距离最短。
【分析】三人跑得一样快,说明速度相同,谁离足球的路程近,谁先抢到。过一点有且只有一条直线与已知直线垂直。从直线外一点到这条直线的线段中,垂直线段最短,这条垂直线段的长度叫做点到直线的距离。
【详解】
典典最先抢到足球,理由:从直线外一点到这条直线的线段中,垂直线段最短;天天、典典、龙龙三人在一条直线上,从足球到这条直线的距离中,典典到足球的距离就是垂线段,距离最短。
【点睛】此题应根据垂线段的性质进行解答。从直线外一点向已知直线画垂直线段和斜线,垂线段最短。
