第五单元《三平行四边形和梯形》同步练习四年级上册数学人教版(含解析)
文档属性
| 名称 | 第五单元《三平行四边形和梯形》同步练习四年级上册数学人教版(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 185.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-09 13:32:46 | ||
图片预览





文档简介
人教版数学四年级上册第五单元《三平行四边形和梯形》课后作业四
学校:___________姓名:___________班级:___________
一、选择题
1.从直线外一点画已知直线的平行线,可以画( )条。
A.1 B.2 C.3 D.无数条
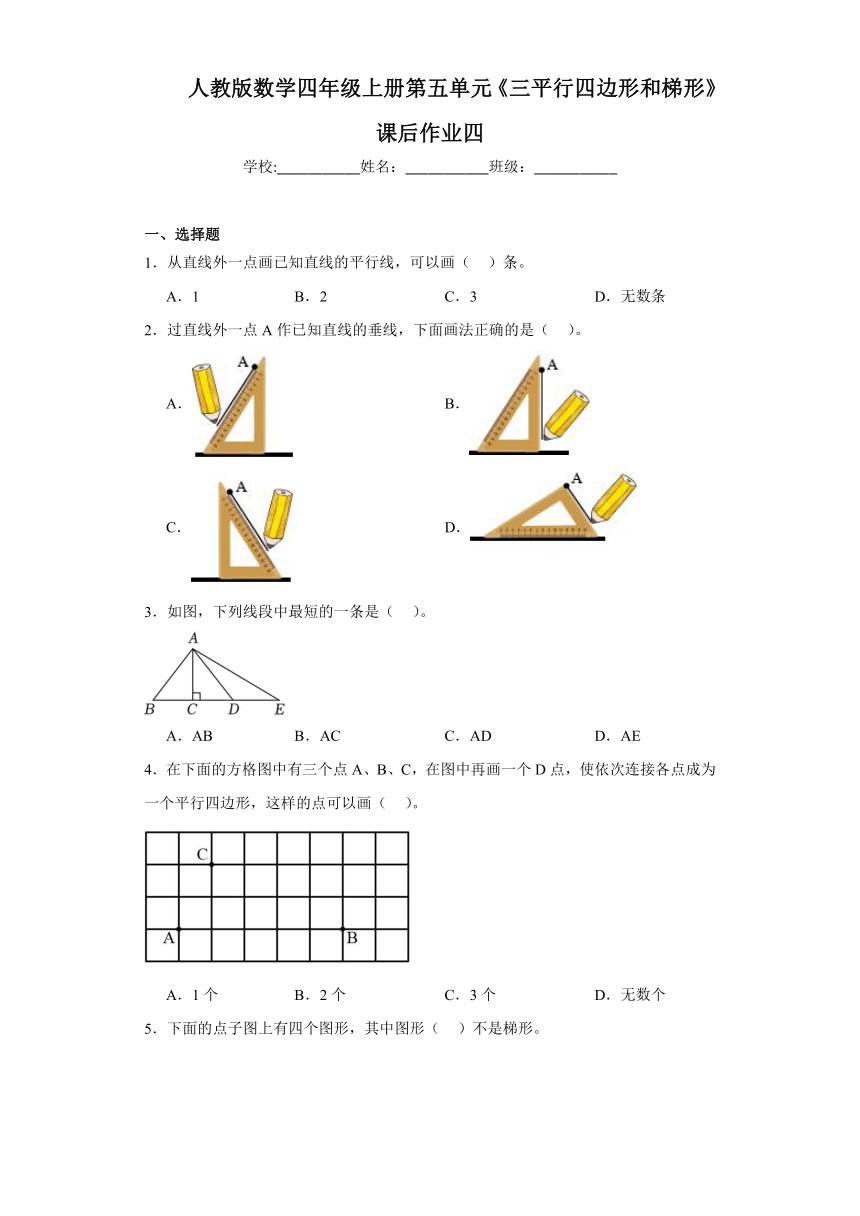
2.过直线外一点A作已知直线的垂线,下面画法正确的是( )。
A. B.
C. D.
3.如图,下列线段中最短的一条是( )。
A.AB B.AC C.AD D.AE
4.在下面的方格图中有三个点A、B、C,在图中再画一个D点,使依次连接各点成为一个平行四边形,这样的点可以画( )。
A.1个 B.2个 C.3个 D.无数个
5.下面的点子图上有四个图形,其中图形( )不是梯形。
A.A B.B C.C D.D
二、填空题
6.如果两条直线都和第三条直线垂直,那么这两条直线互相( )。
7.有4条直线(如图),其中,与直线c垂直的直线有( )条,与直线c相交的直线有( )条。
8.如图中,小正方形的边长是4厘米,大正方形的边长是6厘米。图中共有( )个梯形,其中最大的梯形较短底边是( )厘米,较长底边是( )厘米,高是( )厘米。
9.图中,平行四边形AD边上的高是( )厘米。
10.伸缩门就是利用平行四边形( )的特点制作的。
三、判断题
11.慢慢拉动一个长方形框架把它变成一个平行四边形,它的面积和周长都越来越小。( )
12.在一个梯形中最多有一个直角。( )
13.两个梯形一定能拼成一个平行四边形。( )
14.如下图,聪聪和明明以同样的速度按如图的路线向终点跑去,聪聪先到达。( )
15.图中共有4个平行四边形。( )
四、解答题
16.一块菜地是一个等腰梯形,它的腰长7米,上底长12米,下底比上底长4米,如果在菜地四周围上篱笆,至少需要篱笆多少米?
17.已知平行四边形的周长是48厘米,其中一条边长是9厘米,另一条边长是多少厘米?
18.
(1)量一量,图中∠B=( )°。
(2)在图中找一个点D,使四边形ABCD是一个梯形,请你画出这个梯形。
(3)以线段BC为底,画出这个梯形的高。
参考答案:
1.A
【分析】根据平行的性质:过直线外一点画已知直线的平行线,有且只有一条直线与已知直线平行;据此解答即可。
【详解】在同一平面内,过直线外一点画已知直线的平行线,可以画1条。
故答案为:A
【点睛】此题考查的知识点是平行的性质,关键是正确理解和运用。
2.B
【分析】过直线上或直线外一点作垂线的步骤:把三角尺的一条直角边与已知直线重合;沿着直线移动三角尺,使直线上或直线外的点在三角尺的另一条直角边上;沿三角尺的另一条直角边画一条直线,并画上垂直符号;这条直线就是已知直线的垂线;据此解答。
【详解】根据分析:
A.应该沿着直角边画直线,画法错误;
B.三角尺的一条直角边与已知直线重合,沿三角尺的另一条直角边画一条直线,画法正确;
C.应该沿着直角边画直线,画法错误;
D.应该沿着直角边画直线,画法错误。
故答案为:B
【点睛】掌握直线外一点作垂线的方法是解答本题的关键。
3.B
【分析】连接直线外一点与直线上各点的所有线段中,垂线段最短。可把图看成是三角形ABE,那么在三角形ABE中,线段AC是垂线,据此可作答。
【详解】根据上述分析,在线段AB、AC、AD、AE中,因为线段AC⊥BE,即线段AC是垂线,所以最短的一条是线段AC。
故答案为:B
4.A
【分析】两组对边分别平行的四边形,叫做平行四边形,平行四边形的两组对边分别相等,因此当以AB边为平行四边形的底时,此时有1种画法;依此选择。
【详解】根据分析,画图如下:
由此可知,这样的点可以画1个。
故答案为:A
【点睛】熟练掌握平行四边形的特点,是解答此题的关键。
5.A
【分析】只有一组对边平行的四边形叫做梯形。
【详解】A.图形A没有互相平行的对边,不是梯形;
B.图形B只有一组对边平行,是梯形;
C.图形C只有一组对边平行,是梯形;
D.图形D只有一组对边平行,是梯形。
图形A不是梯形。
故答案为:A
【点睛】熟记梯形的定义是解题关键。
6.平行
【分析】在同一平面内,两条直线相交成直角,这两条直线互相垂直;同一平面内,永不相交的两条直线叫做平行线,组成平行线的两条直线互相平行;依此画图并判断。
【详解】根据分析,画图如下:
由此可知,如果两条直线都与第三条直线垂直,那么这两条直线互相平行。
7. 2 3
【分析】在同一平面内,如果两条直线相交成直角,这两条直线互相垂直,其中一条直线是另一条直线的垂线。
【详解】与直线c垂直的直线有a、b,延长直线c和直线d,直线c和直线d会相交,与直线c相交的直线有a、b、d。
有4条直线(如图),其中,与直线c垂直的直线有(2)条,与直线c相交的直线有(3)条。
【点睛】熟记垂直的定义是解题关键。
8. 3 4 6 10
【分析】根据梯形的定义:只有一组对边平行的四边形是梯形。其中最大的梯形的较短底边是小正方形的边长,较长底边是大正方形的边长。而这个梯形的高是小正方形和大正方形的边长和。
【详解】仔细观察上图:图中共有3个梯形,其中最大的梯形较短底边是4厘米,较长底边是6厘米,4+6=10(厘米),高是10厘米。
【点睛】本题主要考查了梯形的认识,从梯形一条底边上的一点到它对边的垂直线段叫做梯形的高。
9.11
【分析】根据平行四边形的高和底的意义:从平行四边形一条边上的一点到它对边的垂线段是平行四边形的高,这条对边是平行四边形的底,解答此题。
【详解】图中,平行四边形AD边上的高是11厘米。
【点睛】此题主要考查平行四边形的底和高的对应关系的掌握情况。
10.容易变形
【分析】由平行四边形的特性可知,平行四边形具有不稳定性,所以容易变形,伸缩门运用了平行四边形易变形的特性。生活中人们利用这个特性制作很多实用工具,如:升降梯、折叠椅等;据此解答。
【详解】伸缩门就是利用平行四边形容易变形的特点制作的。
【点睛】本题主要考查学生对平行四边形不稳定性知识的掌握和灵活应用。
11.×
【分析】将长方形框架拉成平行四边形,围绕图形一周的长度不变,长不变,宽会变短;平行四边形的面积=底×高;据此解答。
【详解】根据分析:将长方形框架拉成平行四边形,长方形的长相当于平行四边形的底,长不变,宽变短,平行四边形的高小于宽,也就说明面积会变小;而周长不变;所以它的面积和周长都越来越小,所以这个说法是错误的。
故答案为:×
【点睛】掌握长方形和平行四边形的周长与面积的计算方法,是解答本题的关键。
12.×
【分析】梯形:只有一组对边平行的四边形,直角梯形有2个直角;据此解答。
【详解】根据分析:在一个梯形中最多有两个直角,而不是一个,原题说法错误。
故答案为:×
【点睛】此题考查的目的是理解掌握直角梯形的特征。
13.×
【分析】两个相同的梯形能够拼成一个平行四边形。据此解答。
【详解】由分析可知,两个梯形要相同才能够拼成平行四边形,不相同的两个梯形不一定能拼成平行四边形。题目说法错误。
故答案为:×
【点睛】本题主题考查图形的拼组,熟练掌握梯形和平行四边形的特征是解决此题的关键。
14.√
【分析】从图中可知:聪聪跑的是垂直路线,根据连接直线外一点与直线上各点的所有线段中,垂线段最短,可知聪聪先到达。
【详解】根据分析可知:聪聪和明明以同样的速度按如图的路线向终点跑去,聪聪先到达,所以原题说法正确。
故答案为:√
【点睛】本题主要考查点到直线的距离:连接直线外一点与直线上各点的所有线段中,垂线段最短,这条垂线段的长度,叫做点到直线的距离。
15.×
【分析】两组对边分别平行的四边形叫做平行四边形,根据平行四边形的定义和特征,进行判断即可,判断时注意图形组合。
【详解】如下图:
4+4+1=9(个)
独立的小的平行四边形有4个,两个平行四边形组合的平行四边形有4个,四个平行四边形组合的平行四边形有1个,一共有9个平行四边形;故原题干说法错误。
故答案为:×
【点睛】解决本题的关键是熟练掌握平行四边形的定义和特征。
16.42米
【分析】等腰梯形的两腰相等,根据题意可知,上底长+4米=下底长,上底长+下底长+腰长×2=等腰梯形的周长,依此计算并解答。
【详解】12+4=16(米)
12+16+7×2
=12+16+14
=28+14
=42(米)
答:如果在菜地四周围上篱笆,至少需要篱笆42米。
【点睛】此题考查的是等腰梯形的周长的计算,应熟练掌握等腰梯形的特点。
17.15厘米
【分析】根据平行四边形的特点,对边相等可得,平行四边形的周长的求解方法与长方形相似,都是相邻两条边的和的2倍,由此先用周长48厘米除以2,求出相邻两边的和,再减去其中的一条边9厘米,即可求出另一条边。
【详解】48÷2-9
=24-9
=15(厘米)
答:另一条边长是15厘米。
【点睛】本题考查的是平行四边形周长的计算,平行四边形周长等于两邻边和再乘2。
18.(1)60;(2)见详解;(3)见详解
【分析】(1)角的度量方法:量角器的中心与角的顶点重合,0刻度线与角的一边重合,角的另一边所对的量角器上的刻度,就是这个角的度数。
(2)在A点所在横线右边2个格子位置取一点D,连接AD、DC即可得到一个梯形。
(3)从A点作BC的垂线段即为梯形的高。
【详解】(1)经测量,∠B=60°。
(2)(3)见下图:
【点睛】本题主要考查了角的度量和画梯形及梯形高的方法。
学校:___________姓名:___________班级:___________
一、选择题
1.从直线外一点画已知直线的平行线,可以画( )条。
A.1 B.2 C.3 D.无数条
2.过直线外一点A作已知直线的垂线,下面画法正确的是( )。
A. B.
C. D.
3.如图,下列线段中最短的一条是( )。
A.AB B.AC C.AD D.AE
4.在下面的方格图中有三个点A、B、C,在图中再画一个D点,使依次连接各点成为一个平行四边形,这样的点可以画( )。
A.1个 B.2个 C.3个 D.无数个
5.下面的点子图上有四个图形,其中图形( )不是梯形。
A.A B.B C.C D.D
二、填空题
6.如果两条直线都和第三条直线垂直,那么这两条直线互相( )。
7.有4条直线(如图),其中,与直线c垂直的直线有( )条,与直线c相交的直线有( )条。
8.如图中,小正方形的边长是4厘米,大正方形的边长是6厘米。图中共有( )个梯形,其中最大的梯形较短底边是( )厘米,较长底边是( )厘米,高是( )厘米。
9.图中,平行四边形AD边上的高是( )厘米。
10.伸缩门就是利用平行四边形( )的特点制作的。
三、判断题
11.慢慢拉动一个长方形框架把它变成一个平行四边形,它的面积和周长都越来越小。( )
12.在一个梯形中最多有一个直角。( )
13.两个梯形一定能拼成一个平行四边形。( )
14.如下图,聪聪和明明以同样的速度按如图的路线向终点跑去,聪聪先到达。( )
15.图中共有4个平行四边形。( )
四、解答题
16.一块菜地是一个等腰梯形,它的腰长7米,上底长12米,下底比上底长4米,如果在菜地四周围上篱笆,至少需要篱笆多少米?
17.已知平行四边形的周长是48厘米,其中一条边长是9厘米,另一条边长是多少厘米?
18.
(1)量一量,图中∠B=( )°。
(2)在图中找一个点D,使四边形ABCD是一个梯形,请你画出这个梯形。
(3)以线段BC为底,画出这个梯形的高。
参考答案:
1.A
【分析】根据平行的性质:过直线外一点画已知直线的平行线,有且只有一条直线与已知直线平行;据此解答即可。
【详解】在同一平面内,过直线外一点画已知直线的平行线,可以画1条。
故答案为:A
【点睛】此题考查的知识点是平行的性质,关键是正确理解和运用。
2.B
【分析】过直线上或直线外一点作垂线的步骤:把三角尺的一条直角边与已知直线重合;沿着直线移动三角尺,使直线上或直线外的点在三角尺的另一条直角边上;沿三角尺的另一条直角边画一条直线,并画上垂直符号;这条直线就是已知直线的垂线;据此解答。
【详解】根据分析:
A.应该沿着直角边画直线,画法错误;
B.三角尺的一条直角边与已知直线重合,沿三角尺的另一条直角边画一条直线,画法正确;
C.应该沿着直角边画直线,画法错误;
D.应该沿着直角边画直线,画法错误。
故答案为:B
【点睛】掌握直线外一点作垂线的方法是解答本题的关键。
3.B
【分析】连接直线外一点与直线上各点的所有线段中,垂线段最短。可把图看成是三角形ABE,那么在三角形ABE中,线段AC是垂线,据此可作答。
【详解】根据上述分析,在线段AB、AC、AD、AE中,因为线段AC⊥BE,即线段AC是垂线,所以最短的一条是线段AC。
故答案为:B
4.A
【分析】两组对边分别平行的四边形,叫做平行四边形,平行四边形的两组对边分别相等,因此当以AB边为平行四边形的底时,此时有1种画法;依此选择。
【详解】根据分析,画图如下:
由此可知,这样的点可以画1个。
故答案为:A
【点睛】熟练掌握平行四边形的特点,是解答此题的关键。
5.A
【分析】只有一组对边平行的四边形叫做梯形。
【详解】A.图形A没有互相平行的对边,不是梯形;
B.图形B只有一组对边平行,是梯形;
C.图形C只有一组对边平行,是梯形;
D.图形D只有一组对边平行,是梯形。
图形A不是梯形。
故答案为:A
【点睛】熟记梯形的定义是解题关键。
6.平行
【分析】在同一平面内,两条直线相交成直角,这两条直线互相垂直;同一平面内,永不相交的两条直线叫做平行线,组成平行线的两条直线互相平行;依此画图并判断。
【详解】根据分析,画图如下:
由此可知,如果两条直线都与第三条直线垂直,那么这两条直线互相平行。
7. 2 3
【分析】在同一平面内,如果两条直线相交成直角,这两条直线互相垂直,其中一条直线是另一条直线的垂线。
【详解】与直线c垂直的直线有a、b,延长直线c和直线d,直线c和直线d会相交,与直线c相交的直线有a、b、d。
有4条直线(如图),其中,与直线c垂直的直线有(2)条,与直线c相交的直线有(3)条。
【点睛】熟记垂直的定义是解题关键。
8. 3 4 6 10
【分析】根据梯形的定义:只有一组对边平行的四边形是梯形。其中最大的梯形的较短底边是小正方形的边长,较长底边是大正方形的边长。而这个梯形的高是小正方形和大正方形的边长和。
【详解】仔细观察上图:图中共有3个梯形,其中最大的梯形较短底边是4厘米,较长底边是6厘米,4+6=10(厘米),高是10厘米。
【点睛】本题主要考查了梯形的认识,从梯形一条底边上的一点到它对边的垂直线段叫做梯形的高。
9.11
【分析】根据平行四边形的高和底的意义:从平行四边形一条边上的一点到它对边的垂线段是平行四边形的高,这条对边是平行四边形的底,解答此题。
【详解】图中,平行四边形AD边上的高是11厘米。
【点睛】此题主要考查平行四边形的底和高的对应关系的掌握情况。
10.容易变形
【分析】由平行四边形的特性可知,平行四边形具有不稳定性,所以容易变形,伸缩门运用了平行四边形易变形的特性。生活中人们利用这个特性制作很多实用工具,如:升降梯、折叠椅等;据此解答。
【详解】伸缩门就是利用平行四边形容易变形的特点制作的。
【点睛】本题主要考查学生对平行四边形不稳定性知识的掌握和灵活应用。
11.×
【分析】将长方形框架拉成平行四边形,围绕图形一周的长度不变,长不变,宽会变短;平行四边形的面积=底×高;据此解答。
【详解】根据分析:将长方形框架拉成平行四边形,长方形的长相当于平行四边形的底,长不变,宽变短,平行四边形的高小于宽,也就说明面积会变小;而周长不变;所以它的面积和周长都越来越小,所以这个说法是错误的。
故答案为:×
【点睛】掌握长方形和平行四边形的周长与面积的计算方法,是解答本题的关键。
12.×
【分析】梯形:只有一组对边平行的四边形,直角梯形有2个直角;据此解答。
【详解】根据分析:在一个梯形中最多有两个直角,而不是一个,原题说法错误。
故答案为:×
【点睛】此题考查的目的是理解掌握直角梯形的特征。
13.×
【分析】两个相同的梯形能够拼成一个平行四边形。据此解答。
【详解】由分析可知,两个梯形要相同才能够拼成平行四边形,不相同的两个梯形不一定能拼成平行四边形。题目说法错误。
故答案为:×
【点睛】本题主题考查图形的拼组,熟练掌握梯形和平行四边形的特征是解决此题的关键。
14.√
【分析】从图中可知:聪聪跑的是垂直路线,根据连接直线外一点与直线上各点的所有线段中,垂线段最短,可知聪聪先到达。
【详解】根据分析可知:聪聪和明明以同样的速度按如图的路线向终点跑去,聪聪先到达,所以原题说法正确。
故答案为:√
【点睛】本题主要考查点到直线的距离:连接直线外一点与直线上各点的所有线段中,垂线段最短,这条垂线段的长度,叫做点到直线的距离。
15.×
【分析】两组对边分别平行的四边形叫做平行四边形,根据平行四边形的定义和特征,进行判断即可,判断时注意图形组合。
【详解】如下图:
4+4+1=9(个)
独立的小的平行四边形有4个,两个平行四边形组合的平行四边形有4个,四个平行四边形组合的平行四边形有1个,一共有9个平行四边形;故原题干说法错误。
故答案为:×
【点睛】解决本题的关键是熟练掌握平行四边形的定义和特征。
16.42米
【分析】等腰梯形的两腰相等,根据题意可知,上底长+4米=下底长,上底长+下底长+腰长×2=等腰梯形的周长,依此计算并解答。
【详解】12+4=16(米)
12+16+7×2
=12+16+14
=28+14
=42(米)
答:如果在菜地四周围上篱笆,至少需要篱笆42米。
【点睛】此题考查的是等腰梯形的周长的计算,应熟练掌握等腰梯形的特点。
17.15厘米
【分析】根据平行四边形的特点,对边相等可得,平行四边形的周长的求解方法与长方形相似,都是相邻两条边的和的2倍,由此先用周长48厘米除以2,求出相邻两边的和,再减去其中的一条边9厘米,即可求出另一条边。
【详解】48÷2-9
=24-9
=15(厘米)
答:另一条边长是15厘米。
【点睛】本题考查的是平行四边形周长的计算,平行四边形周长等于两邻边和再乘2。
18.(1)60;(2)见详解;(3)见详解
【分析】(1)角的度量方法:量角器的中心与角的顶点重合,0刻度线与角的一边重合,角的另一边所对的量角器上的刻度,就是这个角的度数。
(2)在A点所在横线右边2个格子位置取一点D,连接AD、DC即可得到一个梯形。
(3)从A点作BC的垂线段即为梯形的高。
【详解】(1)经测量,∠B=60°。
(2)(3)见下图:
【点睛】本题主要考查了角的度量和画梯形及梯形高的方法。
