第10章轴对称平移和旋转全章学案(无答案)
文档属性
| 名称 | 第10章轴对称平移和旋转全章学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 472.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-08 00:00:00 | ||
图片预览


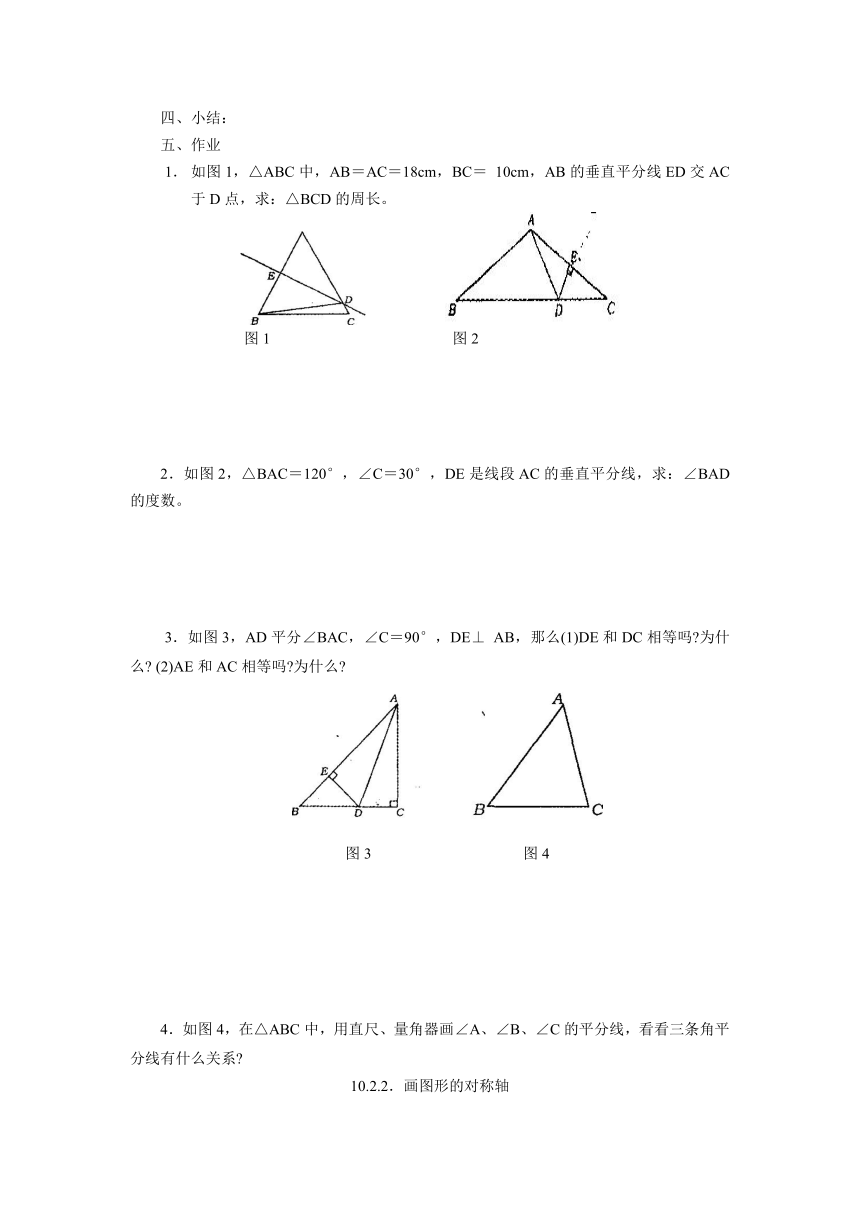
文档简介
第10章 轴对称
10、1生活中的轴对称
学习目的:1.通过展示轴对称图形的图片, ( http: / / www.21cnjy.com )使学生初步认识轴对称图形; 2.通过试验,归纳出轴对称图形概念,能用概念判断一个图形是否是轴对称图形; 3.培养学生的动手试验能力、归纳能力和语言表述能力。
学习重点、难点:轴对称图形的概念是教学重点,判断图形是否是轴对称图形既是教学重点又是教学难点。
学习过程
一、预习
1.认识一些轴对称图形。
( http: / / www.21cnjy.com )
2.课上展开讨论,列举出一些现实生活中有关轴对称的物体和建筑物。
二、新知识
1.试验: 把一张半透明纸对折,然后从折叠处剪出一个图形,展开后会是一个什么样的图形
2.由展示的图片和同学们剪出的图案归纳轴对 ( http: / / www.21cnjy.com )称图形的概念。这些图形如果沿着某条直线对折,对折的两部分是完全重合的,这样的图形称为轴对称图形这条直线叫做这个图形的对称轴。
三、练习
1.要求同学们找出所剪的图案的对称轴,并且用直尺把它画出来。
2.让同学们找对称轴,有的轴对称图形不止一条对称轴。例如:圆、五角星、正方形等。
四、小结
五、作业:第82页习题10.1练习第1、2、3、4题
10、1生活中的轴对称(习题课)
1.请同学们课前预习练习册第110页,预做第111页到第113页的题目,将不会的题目作上重点符号。
2.找出练习册第110页 到第113页的相关题目中出现的相关题型和基本图形,并试找了相对应的问题的解决方法。
10.2.1.简单的轴对称图形
学习目的: 通过动手试验,知道线段是轴对称 ( http: / / www.21cnjy.com )图形,掌握线段的垂直子分线的定义和性质,并学会应用线段垂直平分线性质解决相关问题。知道角是轴对称图形,对称轴是角平分线所在的直线,掌握角平分线的性质,并能运用它解决相关问题。
学习重点:线段垂直平分线上的点到线段两端的距离相等。角平分线上的点到角两边的距离相等。
学习难点:运用线段垂直平分线性质解决问题。运用角平分线性质解决问题。
学习过程 一、复习与预习
1.轴对称图形的定义是什么
2.线段是轴对称图形吗 它的两个端点是否关于某条直线成轴对称
二、新知识
1.认识线段是轴对称图形,引出线段垂直平分线的定义。
线段垂直平分线的定 ( http: / / www.21cnjy.com )义: 称为这条线段的垂直平分线,或中垂线。直线 CD就是线段AB的垂直平分线。
2.线段垂直平分线上的点到线段两端的距离相等。
线段垂直平分线上的点到线段两端的距离 。
3.线段垂直平分线性质的应用举例。
例1.如右图所示,直线MN和DE分别是线段 AB、BC的垂直平分线,它们交于P点,请问PA和 PC相等吗 为什么
4.角是轴对称图形,对称轴是它的角平分线所在的直线。
5.角平分线上的点到角两边的距离相等。
6.角平分线性质应用举例
例1.如下图(1)所示,在△ABC中, ( http: / / www.21cnjy.com )∠C= 90°,BD是角平分线,交AC于点D,DE⊥AB,垂足为点E,AD=3DE。AD和3DC是什么关系 为什么
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
图(1) 图(2)
、
例2.如上图(2),BD垂直平分线段AC,AE⊥BC,垂足为E,交BD于P点,P=3cm,求 P点到直线AB的距离。
三、练习:课本85页练习第1、2、3、4题
四、小结:
五、作业
如图1,△ABC中,AB=AC=18cm,BC= 10cm,AB的垂直平分线ED交AC于D点,求:△BCD的周长。
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
图1 图2
2.如图2,△BAC=120°,∠C=30°,DE是线段AC的垂直平分线,求:∠BAD的度数。
3.如图3,AD平分∠BAC,∠C=90°,DE⊥ AB,那么(1)DE和DC相等吗 为什么 (2)AE和AC相等吗 为什么
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
图3 图4
4.如图4,在△ABC中,用直尺、量角器画∠A、∠B、∠C的平分线,看看三条角平分线有什么关系
10.2.2.画图形的对称轴
学习目的:掌握用“连结对称点的线段被对称轴垂直平分”验证一个图形是不是轴对称图形,并请熟练画出轴对称图形的对称轴。
学习重点:画轴对称图形的对称轴。
学习难点:归纳总结画轴对称图形对称轴的方法。
学习过程: 一、复习与预习
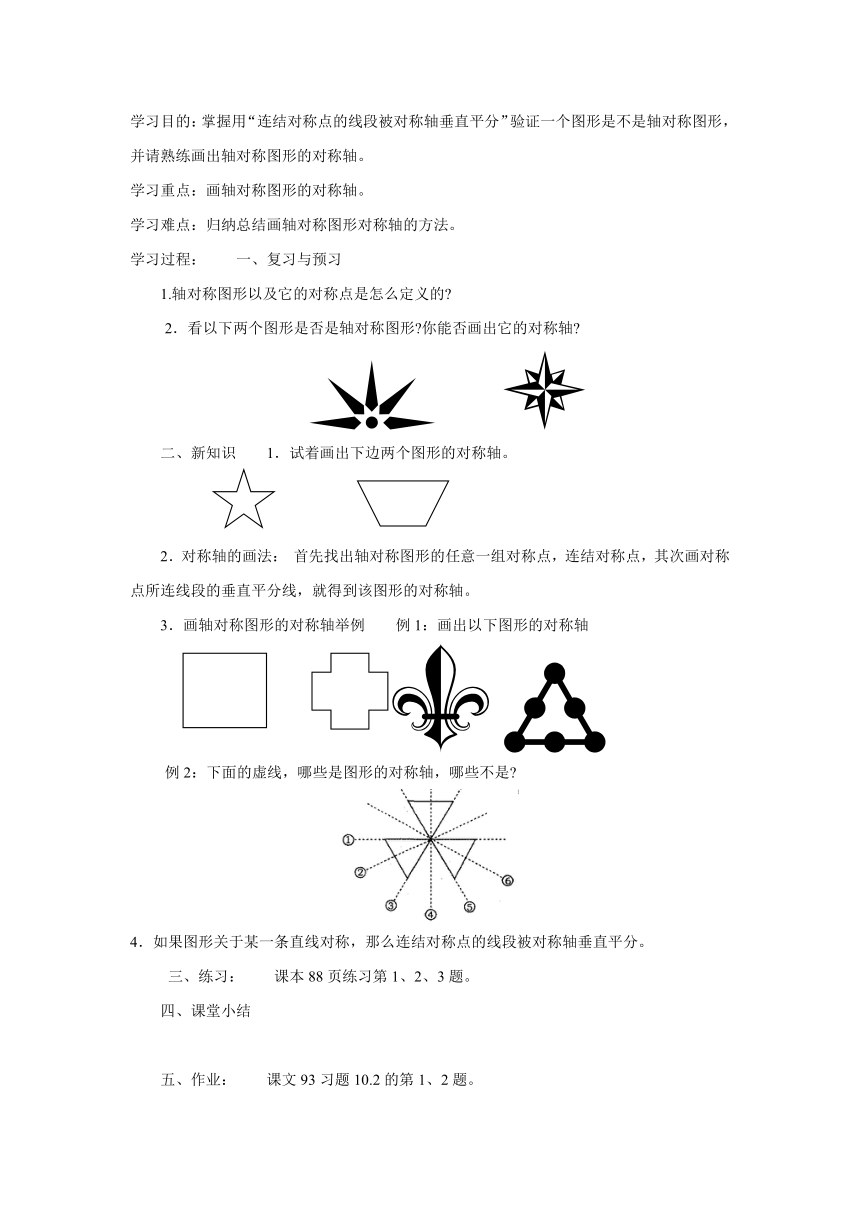
1.轴对称图形以及它的对称点是怎么定义的
2.看以下两个图形是否是轴对称图形 你能否画出它的对称轴
( http: / / www.21cnjy.com )
二、新知识 1.试着画出下边两个图形的对称轴。
2.对称轴的画法: 首先找出轴对称图形的任意一组对称点,连结对称点,其次画对称点所连线段的垂直平分线,就得到该图形的对称轴。
3.画轴对称图形的对称轴举例 例1:画出以下图形的对称轴
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
例2:下面的虚线,哪些是图形的对称轴,哪些不是
( http: / / www.21cnjy.com )
4.如果图形关于某一条直线对称,那么连结对称点的线段被对称轴垂直平分。
三、练习: 课本88页练习第1、2、3题。
四、课堂小结
五、作业: 课文93习题10.2的第1、2题。
10.2.3.画轴对称图形
学习目的 :
1.能够按要求作出简单平面图形经过一次对称后的图形。
2.通过画轴对称图形,增强学习几何的趣味感,培养审美情操。
学习重点:识别轴对称图与画轴对称图形的对称轴。
学习难点:区别轴对称与轴对称图形两个不同的概念。
学习过程
一、复习与预习:
1.什么是轴对称图形 2.请你标出图中,A、B、C三点的对称点。
A
B
C
二、新知识: 如果有一个图形、一条直线,那么如何画出这个图形关于这条直线的对称图形呢
1.请同学们尝试解决以下问题;
如图(1),实线所构成的图形为已知图形,虚线为对称轴,请画出已知图形的轴对称图形。
( http: / / www.21cnjy.com )
(1)你可以通过什么方法来验证你画的是否正确
(2)和其他同学比较一下,你的方法是最简单的吗
例1.已知△ABC,直线l,画出△ABC关于直线l的对称图形。
(1)本题与上面的那些图比较有什么相同点和不同点
(2)你能否从上面的那些图的画法中得到启示,帮助你解决本题
A
B C
三、练习: P90练习第1、2题。
四、小结
五、作业: P93习题10.2第3、4题。
10.2.4.设计轴对称图案
学习目的 :1.能设计简单的轴对称图案。 2.能够欣赏现实生活中的轴对称图形。
学习重点:利用对称轴进行图案设计。
学习难点;寻找对称轴以及如何利用对称轴作轴对称图形。
学习过程:一、复习与预习
1.如图(1),请画出△ABC的关于直线l对称的图形。
A l A
B C B C
图(1) 图(2)
2.如图(2),等边△ABC是轴对称图形吗 如果是,它有几条对称轴 画画试试看。
二、新知识
如图(3)是一个轴对称图形。
问:1.有多少条对称轴呢
2.可以利用轴对称性来画出它吗
三、练习: P92练习1、2
四、小结
10.2.轴对称图(习题课)
1.请同学们课前预习练习册第117-118页,预做第118页到第122页的题目,将不会的题目作上重点符号。
2.找出练习册第117页 到第122页的相关题目中出现的相关题型和基本图形,并试找了相对应的问题的解决方法。
10.3.1.等腰三角形
学习目的: 1.了解等腰三角 ( http: / / www.21cnjy.com )形的有关概念,掌握等腰三角形的性质。 2.通过探索等腰三角形的性质,进一步经历观察、实验、推理、交流等活动。
学习重点:等腰三角形等边对等角性质。
学习难点:通过操作,如何观察、分析、归纳得出等腰三角形性质。
学习过程: 一、复习与预习
1.让学生在练习本上画一个 ( http: / / www.21cnjy.com )等腰三角形,标出字母,问什么样的三角形是等腰三角形 △ABC中,如果有两边AB=AC,那么它是等腰三角形。
2.日常生活中,哪些物体具有等腰三角形的形象
二、新知识
相等的两边AB、AC都叫做腰,另外一边BC叫做底边,两腰的夹角∠BAC,叫做顶角,腰和底边的夹角∠ABC、∠ACB叫做底角。
等腰三角形的两个底角相等(简写成“等边对等角”)。
等腰三角形的顶角平分线,底边上的高和底边上的中线互相重合 (简称“三线合一”)。
例l已知:在△ABC中,AB=AC,∠B=80°,求∠C和∠A的度数。
在等腰三角形中,有一种特殊的情况,就是底边与腰相等,这时,三角形三边都相等。我们把三条边都相等的三角形叫做等边三角形。
等边三角形的各角都相等,并且每一个角都等于60°。
等边三角形是轴对称图形吗 如果是,有几条对称轴
等边三角形也称为正三角形。
例1.在△ABC中,AB=AC,D是BC边上的中点,∠B=30°,求∠1和∠ADC的度数。
三、练习: P97 练习1、2、3
1.判断下列命题,对的打“√”,错的打“×”。
a.等腰三角形的角平分线,中线和高互相重合( )
b.有一个角是60°的等腰三角形,其它两个内角也为60°( )
2.如图(2),在△ABC中,已知AB=AC,AD为∠BAC的平分线,且∠2=25°,求∠ADB和∠B的度数。
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
3.如图(3),△ABC是等边三角形,BD、CE是中线,求∠CBD,∠BOE,∠BOC,∠EOD的度数。
4.填空:在△ABC中,AB=AC,D在BC上,
1).如果AD⊥BC,那么∠BAD=∠______,BD=_______
2).如果∠BAD=∠CAD,那么AD⊥_____,BD=______
3).如果BD=CD,那么∠BAD=∠_______,AD⊥______
四、小结
五、作业: P99习题第1、2、3题。
10.3.1.等腰三角形(习题课)
1.请同学们课前预习练习册第123页,预做第123页到第125页的题目,将不会的题目作上重点符号。
2.找出练习册第123页 到第125页的相关题目中出现的相关题型和基本图形,并试找了相对应的问题的解决方法。
10.3.2.等腰三角形的识别
学习目的: 1.通过探索一个三角形是等腰三角形的条件,培养探索能力。 2.能利用等腰三角形的条件,正确判断某个三角形是否为等腰三角形。
学习重点:让学生掌握一个三角形是等腰三角形的条件和正确应用。
学习难点:一个三角形是等腰三角形的条件的正确文字叙述。
学习过程: 一、复习与预习
1.等腰三角形具有哪些性质
2. 等腰三角形的两底角相等,底边上的高、中线及顶角平分线“三线合一”。
二、新知识
对于一个三角形,怎样识别它是不是等腰三角形呢 我们已经知道的方法是看它是否有两条边相等。这一节,我们再学习另一种识别方法。
我们已学过,等腰三角形的两个底角相等,反过来,在一个三角形中,如果有两个角相等,那么它是等腰三角形吗
如果一个三角形有两个角相等,那么这两个角所对的边也相等,简写成“等角对等边”。
例1.在△ABC中,已知∠A=40°,∠B=70°,判断△ABC是什么三角形,为什么
问:三个角都是60°的三角形是等边三角形吗 你能说明理由吗
等腰直角三角形:顶角是直角的等腰三角形是等腰直角三角形。
问:你能说出等腰直角三角形各角的大小吗
问:请你画一个等腰直角三角形,使∠C=90°,CD是底边上的高,数一数图中共有几个等腰直角三角形
三、练习: P99练习l、2、3。
四、小结
10.3.2.等腰三角形的识别(习题课)
1.请同学们课前预习练习册第125页,预做第126页到第127页的题目,将不会的题目作上重点符号。
2.找出练习册第125页 到第127页的相关题目中出现的相关题型和基本图形,并试找了相对应的问题的解决方法。
第10章 (习题课)
一、请同学们课前预习练习册第128页,预做第128页到第130页的题目,将不会的题目作上重点符号。
二、找出练习册第128页 到第130页的相关题目中出现的相关题型和基本图形,并试找了相对应的问题的解决方法。
三、完成下面题目:
1.下列图案是轴对称图形的有( )
A.1个 D.2个 C.3个 D.4个
2.如右图所示,已知,OC平分∠AOB,D是OC上一点,DE⊥OA,DF⊥OB,垂足为E、F点,那么
(1)∠DEF与∠DFE相等吗 为什么
(2)OE与OF相等吗 为什么
3.如右图所示,已知AB=AC,DE垂直平分 ( http: / / www.21cnjy.com )AB交AC、AB于D、E两点,若AB=12cm,BC=l0cm,∠A=49°14′54″.求△BCD的周长和∠DBC度数。
10、1生活中的轴对称
学习目的:1.通过展示轴对称图形的图片, ( http: / / www.21cnjy.com )使学生初步认识轴对称图形; 2.通过试验,归纳出轴对称图形概念,能用概念判断一个图形是否是轴对称图形; 3.培养学生的动手试验能力、归纳能力和语言表述能力。
学习重点、难点:轴对称图形的概念是教学重点,判断图形是否是轴对称图形既是教学重点又是教学难点。
学习过程
一、预习
1.认识一些轴对称图形。
( http: / / www.21cnjy.com )
2.课上展开讨论,列举出一些现实生活中有关轴对称的物体和建筑物。
二、新知识
1.试验: 把一张半透明纸对折,然后从折叠处剪出一个图形,展开后会是一个什么样的图形
2.由展示的图片和同学们剪出的图案归纳轴对 ( http: / / www.21cnjy.com )称图形的概念。这些图形如果沿着某条直线对折,对折的两部分是完全重合的,这样的图形称为轴对称图形这条直线叫做这个图形的对称轴。
三、练习
1.要求同学们找出所剪的图案的对称轴,并且用直尺把它画出来。
2.让同学们找对称轴,有的轴对称图形不止一条对称轴。例如:圆、五角星、正方形等。
四、小结
五、作业:第82页习题10.1练习第1、2、3、4题
10、1生活中的轴对称(习题课)
1.请同学们课前预习练习册第110页,预做第111页到第113页的题目,将不会的题目作上重点符号。
2.找出练习册第110页 到第113页的相关题目中出现的相关题型和基本图形,并试找了相对应的问题的解决方法。
10.2.1.简单的轴对称图形
学习目的: 通过动手试验,知道线段是轴对称 ( http: / / www.21cnjy.com )图形,掌握线段的垂直子分线的定义和性质,并学会应用线段垂直平分线性质解决相关问题。知道角是轴对称图形,对称轴是角平分线所在的直线,掌握角平分线的性质,并能运用它解决相关问题。
学习重点:线段垂直平分线上的点到线段两端的距离相等。角平分线上的点到角两边的距离相等。
学习难点:运用线段垂直平分线性质解决问题。运用角平分线性质解决问题。
学习过程 一、复习与预习
1.轴对称图形的定义是什么
2.线段是轴对称图形吗 它的两个端点是否关于某条直线成轴对称
二、新知识
1.认识线段是轴对称图形,引出线段垂直平分线的定义。
线段垂直平分线的定 ( http: / / www.21cnjy.com )义: 称为这条线段的垂直平分线,或中垂线。直线 CD就是线段AB的垂直平分线。
2.线段垂直平分线上的点到线段两端的距离相等。
线段垂直平分线上的点到线段两端的距离 。
3.线段垂直平分线性质的应用举例。
例1.如右图所示,直线MN和DE分别是线段 AB、BC的垂直平分线,它们交于P点,请问PA和 PC相等吗 为什么
4.角是轴对称图形,对称轴是它的角平分线所在的直线。
5.角平分线上的点到角两边的距离相等。
6.角平分线性质应用举例
例1.如下图(1)所示,在△ABC中, ( http: / / www.21cnjy.com )∠C= 90°,BD是角平分线,交AC于点D,DE⊥AB,垂足为点E,AD=3DE。AD和3DC是什么关系 为什么
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
图(1) 图(2)
、
例2.如上图(2),BD垂直平分线段AC,AE⊥BC,垂足为E,交BD于P点,P=3cm,求 P点到直线AB的距离。
三、练习:课本85页练习第1、2、3、4题
四、小结:
五、作业
如图1,△ABC中,AB=AC=18cm,BC= 10cm,AB的垂直平分线ED交AC于D点,求:△BCD的周长。
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
图1 图2
2.如图2,△BAC=120°,∠C=30°,DE是线段AC的垂直平分线,求:∠BAD的度数。
3.如图3,AD平分∠BAC,∠C=90°,DE⊥ AB,那么(1)DE和DC相等吗 为什么 (2)AE和AC相等吗 为什么
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
图3 图4
4.如图4,在△ABC中,用直尺、量角器画∠A、∠B、∠C的平分线,看看三条角平分线有什么关系
10.2.2.画图形的对称轴
学习目的:掌握用“连结对称点的线段被对称轴垂直平分”验证一个图形是不是轴对称图形,并请熟练画出轴对称图形的对称轴。
学习重点:画轴对称图形的对称轴。
学习难点:归纳总结画轴对称图形对称轴的方法。
学习过程: 一、复习与预习
1.轴对称图形以及它的对称点是怎么定义的
2.看以下两个图形是否是轴对称图形 你能否画出它的对称轴
( http: / / www.21cnjy.com )
二、新知识 1.试着画出下边两个图形的对称轴。
2.对称轴的画法: 首先找出轴对称图形的任意一组对称点,连结对称点,其次画对称点所连线段的垂直平分线,就得到该图形的对称轴。
3.画轴对称图形的对称轴举例 例1:画出以下图形的对称轴
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
例2:下面的虚线,哪些是图形的对称轴,哪些不是
( http: / / www.21cnjy.com )
4.如果图形关于某一条直线对称,那么连结对称点的线段被对称轴垂直平分。
三、练习: 课本88页练习第1、2、3题。
四、课堂小结
五、作业: 课文93习题10.2的第1、2题。
10.2.3.画轴对称图形
学习目的 :
1.能够按要求作出简单平面图形经过一次对称后的图形。
2.通过画轴对称图形,增强学习几何的趣味感,培养审美情操。
学习重点:识别轴对称图与画轴对称图形的对称轴。
学习难点:区别轴对称与轴对称图形两个不同的概念。
学习过程
一、复习与预习:
1.什么是轴对称图形 2.请你标出图中,A、B、C三点的对称点。
A
B
C
二、新知识: 如果有一个图形、一条直线,那么如何画出这个图形关于这条直线的对称图形呢
1.请同学们尝试解决以下问题;
如图(1),实线所构成的图形为已知图形,虚线为对称轴,请画出已知图形的轴对称图形。
( http: / / www.21cnjy.com )
(1)你可以通过什么方法来验证你画的是否正确
(2)和其他同学比较一下,你的方法是最简单的吗
例1.已知△ABC,直线l,画出△ABC关于直线l的对称图形。
(1)本题与上面的那些图比较有什么相同点和不同点
(2)你能否从上面的那些图的画法中得到启示,帮助你解决本题
A
B C
三、练习: P90练习第1、2题。
四、小结
五、作业: P93习题10.2第3、4题。
10.2.4.设计轴对称图案
学习目的 :1.能设计简单的轴对称图案。 2.能够欣赏现实生活中的轴对称图形。
学习重点:利用对称轴进行图案设计。
学习难点;寻找对称轴以及如何利用对称轴作轴对称图形。
学习过程:一、复习与预习
1.如图(1),请画出△ABC的关于直线l对称的图形。
A l A
B C B C
图(1) 图(2)
2.如图(2),等边△ABC是轴对称图形吗 如果是,它有几条对称轴 画画试试看。
二、新知识
如图(3)是一个轴对称图形。
问:1.有多少条对称轴呢
2.可以利用轴对称性来画出它吗
三、练习: P92练习1、2
四、小结
10.2.轴对称图(习题课)
1.请同学们课前预习练习册第117-118页,预做第118页到第122页的题目,将不会的题目作上重点符号。
2.找出练习册第117页 到第122页的相关题目中出现的相关题型和基本图形,并试找了相对应的问题的解决方法。
10.3.1.等腰三角形
学习目的: 1.了解等腰三角 ( http: / / www.21cnjy.com )形的有关概念,掌握等腰三角形的性质。 2.通过探索等腰三角形的性质,进一步经历观察、实验、推理、交流等活动。
学习重点:等腰三角形等边对等角性质。
学习难点:通过操作,如何观察、分析、归纳得出等腰三角形性质。
学习过程: 一、复习与预习
1.让学生在练习本上画一个 ( http: / / www.21cnjy.com )等腰三角形,标出字母,问什么样的三角形是等腰三角形 △ABC中,如果有两边AB=AC,那么它是等腰三角形。
2.日常生活中,哪些物体具有等腰三角形的形象
二、新知识
相等的两边AB、AC都叫做腰,另外一边BC叫做底边,两腰的夹角∠BAC,叫做顶角,腰和底边的夹角∠ABC、∠ACB叫做底角。
等腰三角形的两个底角相等(简写成“等边对等角”)。
等腰三角形的顶角平分线,底边上的高和底边上的中线互相重合 (简称“三线合一”)。
例l已知:在△ABC中,AB=AC,∠B=80°,求∠C和∠A的度数。
在等腰三角形中,有一种特殊的情况,就是底边与腰相等,这时,三角形三边都相等。我们把三条边都相等的三角形叫做等边三角形。
等边三角形的各角都相等,并且每一个角都等于60°。
等边三角形是轴对称图形吗 如果是,有几条对称轴
等边三角形也称为正三角形。
例1.在△ABC中,AB=AC,D是BC边上的中点,∠B=30°,求∠1和∠ADC的度数。
三、练习: P97 练习1、2、3
1.判断下列命题,对的打“√”,错的打“×”。
a.等腰三角形的角平分线,中线和高互相重合( )
b.有一个角是60°的等腰三角形,其它两个内角也为60°( )
2.如图(2),在△ABC中,已知AB=AC,AD为∠BAC的平分线,且∠2=25°,求∠ADB和∠B的度数。
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
3.如图(3),△ABC是等边三角形,BD、CE是中线,求∠CBD,∠BOE,∠BOC,∠EOD的度数。
4.填空:在△ABC中,AB=AC,D在BC上,
1).如果AD⊥BC,那么∠BAD=∠______,BD=_______
2).如果∠BAD=∠CAD,那么AD⊥_____,BD=______
3).如果BD=CD,那么∠BAD=∠_______,AD⊥______
四、小结
五、作业: P99习题第1、2、3题。
10.3.1.等腰三角形(习题课)
1.请同学们课前预习练习册第123页,预做第123页到第125页的题目,将不会的题目作上重点符号。
2.找出练习册第123页 到第125页的相关题目中出现的相关题型和基本图形,并试找了相对应的问题的解决方法。
10.3.2.等腰三角形的识别
学习目的: 1.通过探索一个三角形是等腰三角形的条件,培养探索能力。 2.能利用等腰三角形的条件,正确判断某个三角形是否为等腰三角形。
学习重点:让学生掌握一个三角形是等腰三角形的条件和正确应用。
学习难点:一个三角形是等腰三角形的条件的正确文字叙述。
学习过程: 一、复习与预习
1.等腰三角形具有哪些性质
2. 等腰三角形的两底角相等,底边上的高、中线及顶角平分线“三线合一”。
二、新知识
对于一个三角形,怎样识别它是不是等腰三角形呢 我们已经知道的方法是看它是否有两条边相等。这一节,我们再学习另一种识别方法。
我们已学过,等腰三角形的两个底角相等,反过来,在一个三角形中,如果有两个角相等,那么它是等腰三角形吗
如果一个三角形有两个角相等,那么这两个角所对的边也相等,简写成“等角对等边”。
例1.在△ABC中,已知∠A=40°,∠B=70°,判断△ABC是什么三角形,为什么
问:三个角都是60°的三角形是等边三角形吗 你能说明理由吗
等腰直角三角形:顶角是直角的等腰三角形是等腰直角三角形。
问:你能说出等腰直角三角形各角的大小吗
问:请你画一个等腰直角三角形,使∠C=90°,CD是底边上的高,数一数图中共有几个等腰直角三角形
三、练习: P99练习l、2、3。
四、小结
10.3.2.等腰三角形的识别(习题课)
1.请同学们课前预习练习册第125页,预做第126页到第127页的题目,将不会的题目作上重点符号。
2.找出练习册第125页 到第127页的相关题目中出现的相关题型和基本图形,并试找了相对应的问题的解决方法。
第10章 (习题课)
一、请同学们课前预习练习册第128页,预做第128页到第130页的题目,将不会的题目作上重点符号。
二、找出练习册第128页 到第130页的相关题目中出现的相关题型和基本图形,并试找了相对应的问题的解决方法。
三、完成下面题目:
1.下列图案是轴对称图形的有( )
A.1个 D.2个 C.3个 D.4个
2.如右图所示,已知,OC平分∠AOB,D是OC上一点,DE⊥OA,DF⊥OB,垂足为E、F点,那么
(1)∠DEF与∠DFE相等吗 为什么
(2)OE与OF相等吗 为什么
3.如右图所示,已知AB=AC,DE垂直平分 ( http: / / www.21cnjy.com )AB交AC、AB于D、E两点,若AB=12cm,BC=l0cm,∠A=49°14′54″.求△BCD的周长和∠DBC度数。
