人教版五年级下册数学《长方体和正方体的体积》(课件)(共21张PPT)
文档属性
| 名称 | 人教版五年级下册数学《长方体和正方体的体积》(课件)(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 655.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-09 20:00:24 | ||
图片预览





文档简介
(共21张PPT)
长方体的体积
北师大版五年级下册数学
教学目录
1.复习导入
2.探索新知
4.小结作业
3.内化巩固
复习导入
填一填
(1)物体( )叫做物体的体积。
(2)常用的体积单位有:( )、( )、 ( );
常用的容积单位有:( )、( )。
(3)1立方分米=( )升 1立方厘米=( )毫升
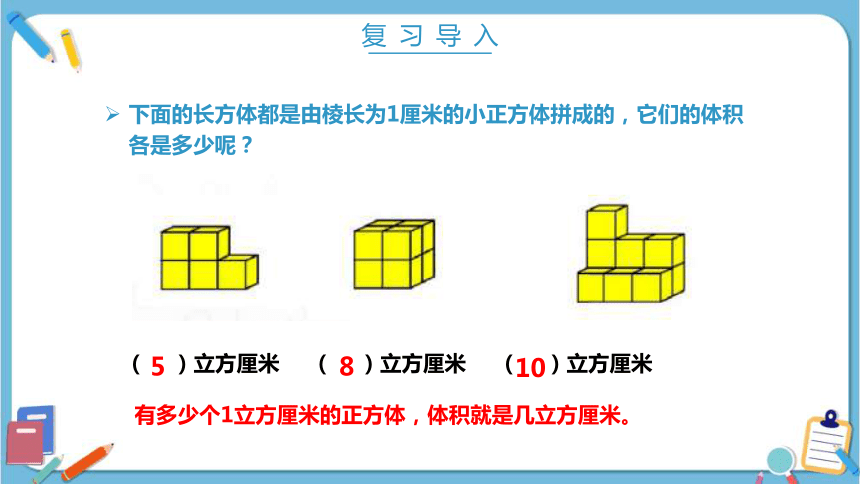
有多少个1立方厘米的正方体,体积就是几立方厘米。
( )立方厘米 ( )立方厘米 ( )立方厘米
5
8
10
复习导入
下面的长方体都是由棱长为1厘米的小正方体拼成的,它们的体积各是多少呢?
面 体
关于长方体你们有什么想知道的吗?
探索新知
探索新知
下面两款牙膏盒,哪一个盒子的体积更大呢?
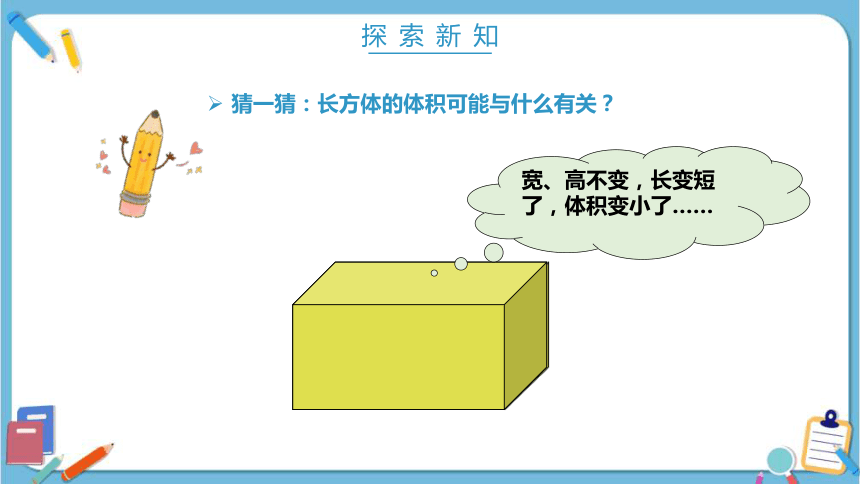
宽、高不变,长变短了,体积变小了……
探索新知
猜一猜:长方体的体积可能与什么有关?
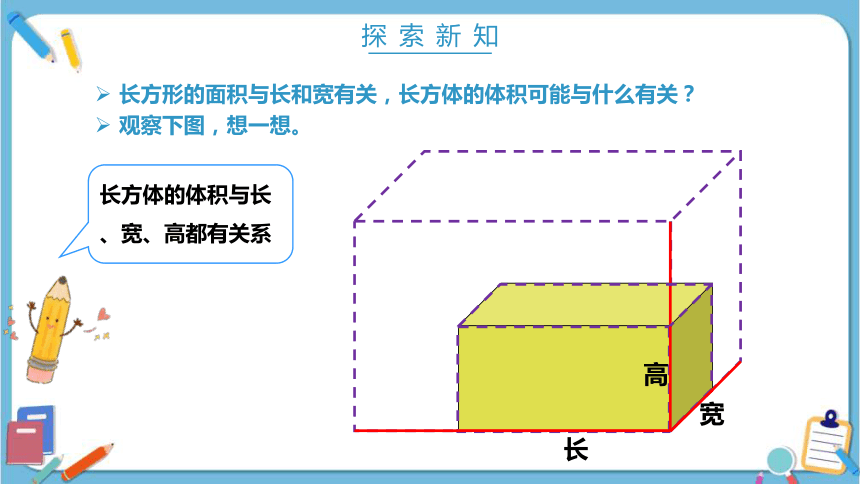
长方体的体积与长、宽、高都有关系
高
宽
长
探索新知
长方形的面积与长和宽有关,长方体的体积可能与什么有关?
观察下图,想一想。
合作要求:
(1)用一些相同的小正方体(棱长为1厘米)摆出4种不同的长方体,记录这些长方体的体积与长、宽、高。
(2)小组合作完成,一个人摆,另一个人记录数据并完成表格,验证你的猜想。
探索新知
摆一摆,长方体的体积与长、宽、高有什么关系呢?
长/cm 宽/cm 高/cm 小正方体数量/个 体积/cm3
第1个长方体
第2个长方体
第3个长方体
第4个长方体
4 3 1 12 12
3 2 2 12 12
12 1 1 12 12
6 2 1 12 12
探索新知
观察表格中的数据,你发现什么?
长/cm 宽/cm 高/cm 小正方体数量/个 体积/cm3
第1个长方体
第2个长方体
第3个长方体
第4个长方体
4 3 1 12 12
3 2 2 12 12
12 1 1 12 12
6 2 1 12 12
小正方体的数量等于长方体体积。
长方体的体积正好是长、宽、高的乘积。
探索新知
观察表格中的数据,你发现什么?
长方体中包含有多少个1立方厘米的正方体,
长方体的体积就是多少立方厘米。
探索新知
为什么小正方体的数量等于长方体的体积
长×宽算的是长方体的一层摆了多少个小正方体(体积单位)。
高表示有几层,再乘高代表的是这个长方体中小正方体的数量。
有多少个1立方厘米的体积单位,它的体积就是多少立方厘米。
探索新知
长方体的体积为什么等于长×宽×高呢?
长方体的体积=长×宽×高
…
…
…
…
=
×
×
=
高
宽
长
探索新知
5
体积=长×宽×高=5×3×4=60(dm3)
内化巩固
用棱长为1dm的小正方体(体积单位)摆长方体,
一行可以摆( )个,摆( )行,一层就摆了( )个,摆了( )层,一共用了( )个这样的体积单位,所以长方体的体积是( )立方分米。
先填一填,再算一算(单位:dm)
4
15
60
5
4
3
3
60
20×6×8=960(cm3)
内化巩固
比一比
长:20cm
宽:6cm
高:8cm
长:18cm
宽:7cm
高:8cm
18×7×8=1008(cm3)
答:第二个牙膏盒的体积更大。
正方体的体积=棱长×棱长×棱长
正方体是特殊的长方体,长方体的体积是“长×宽×高”。
=
=
×
×
如何计算正方体的体积呢?与同伴交流你的想法。
内化巩固
一个正方体,棱长总和是48厘米,它的体积是多少立方厘米?
48÷12=4(厘米)
4×4×4=64(立方厘米)
答:它的体积是64立方厘米。
内化巩固
长方体的体积=长×宽×高
V=a×b×h = abh
正方体的体积=棱长×棱长×棱长
V=a×a×a=a3
小结作业
要计算长方体的体积,就是看它包含多少个体积单位。
如:一行可以摆( )个体积单位,摆( )行,摆了( )层,一共用了( )个这样的体积单位,所以长方体的体积是( )。
小结作业
请完成教材练一练的习题。
测量生活中的长方体或正方体体积。
写一篇数学日记,记录你对长方体体积的认识或疑惑。
谢谢观看!
长方体的体积
北师大版五年级下册数学
教学目录
1.复习导入
2.探索新知
4.小结作业
3.内化巩固
复习导入
填一填
(1)物体( )叫做物体的体积。
(2)常用的体积单位有:( )、( )、 ( );
常用的容积单位有:( )、( )。
(3)1立方分米=( )升 1立方厘米=( )毫升
有多少个1立方厘米的正方体,体积就是几立方厘米。
( )立方厘米 ( )立方厘米 ( )立方厘米
5
8
10
复习导入
下面的长方体都是由棱长为1厘米的小正方体拼成的,它们的体积各是多少呢?
面 体
关于长方体你们有什么想知道的吗?
探索新知
探索新知
下面两款牙膏盒,哪一个盒子的体积更大呢?
宽、高不变,长变短了,体积变小了……
探索新知
猜一猜:长方体的体积可能与什么有关?
长方体的体积与长、宽、高都有关系
高
宽
长
探索新知
长方形的面积与长和宽有关,长方体的体积可能与什么有关?
观察下图,想一想。
合作要求:
(1)用一些相同的小正方体(棱长为1厘米)摆出4种不同的长方体,记录这些长方体的体积与长、宽、高。
(2)小组合作完成,一个人摆,另一个人记录数据并完成表格,验证你的猜想。
探索新知
摆一摆,长方体的体积与长、宽、高有什么关系呢?
长/cm 宽/cm 高/cm 小正方体数量/个 体积/cm3
第1个长方体
第2个长方体
第3个长方体
第4个长方体
4 3 1 12 12
3 2 2 12 12
12 1 1 12 12
6 2 1 12 12
探索新知
观察表格中的数据,你发现什么?
长/cm 宽/cm 高/cm 小正方体数量/个 体积/cm3
第1个长方体
第2个长方体
第3个长方体
第4个长方体
4 3 1 12 12
3 2 2 12 12
12 1 1 12 12
6 2 1 12 12
小正方体的数量等于长方体体积。
长方体的体积正好是长、宽、高的乘积。
探索新知
观察表格中的数据,你发现什么?
长方体中包含有多少个1立方厘米的正方体,
长方体的体积就是多少立方厘米。
探索新知
为什么小正方体的数量等于长方体的体积
长×宽算的是长方体的一层摆了多少个小正方体(体积单位)。
高表示有几层,再乘高代表的是这个长方体中小正方体的数量。
有多少个1立方厘米的体积单位,它的体积就是多少立方厘米。
探索新知
长方体的体积为什么等于长×宽×高呢?
长方体的体积=长×宽×高
…
…
…
…
=
×
×
=
高
宽
长
探索新知
5
体积=长×宽×高=5×3×4=60(dm3)
内化巩固
用棱长为1dm的小正方体(体积单位)摆长方体,
一行可以摆( )个,摆( )行,一层就摆了( )个,摆了( )层,一共用了( )个这样的体积单位,所以长方体的体积是( )立方分米。
先填一填,再算一算(单位:dm)
4
15
60
5
4
3
3
60
20×6×8=960(cm3)
内化巩固
比一比
长:20cm
宽:6cm
高:8cm
长:18cm
宽:7cm
高:8cm
18×7×8=1008(cm3)
答:第二个牙膏盒的体积更大。
正方体的体积=棱长×棱长×棱长
正方体是特殊的长方体,长方体的体积是“长×宽×高”。
=
=
×
×
如何计算正方体的体积呢?与同伴交流你的想法。
内化巩固
一个正方体,棱长总和是48厘米,它的体积是多少立方厘米?
48÷12=4(厘米)
4×4×4=64(立方厘米)
答:它的体积是64立方厘米。
内化巩固
长方体的体积=长×宽×高
V=a×b×h = abh
正方体的体积=棱长×棱长×棱长
V=a×a×a=a3
小结作业
要计算长方体的体积,就是看它包含多少个体积单位。
如:一行可以摆( )个体积单位,摆( )行,摆了( )层,一共用了( )个这样的体积单位,所以长方体的体积是( )。
小结作业
请完成教材练一练的习题。
测量生活中的长方体或正方体体积。
写一篇数学日记,记录你对长方体体积的认识或疑惑。
谢谢观看!
