1.8 小数的意义和加减法(复习课) 逆向教学设计(表格式)
文档属性
| 名称 | 1.8 小数的意义和加减法(复习课) 逆向教学设计(表格式) |
|
|
| 格式 | docx | ||
| 文件大小 | 833.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-08 18:00:44 | ||
图片预览




文档简介
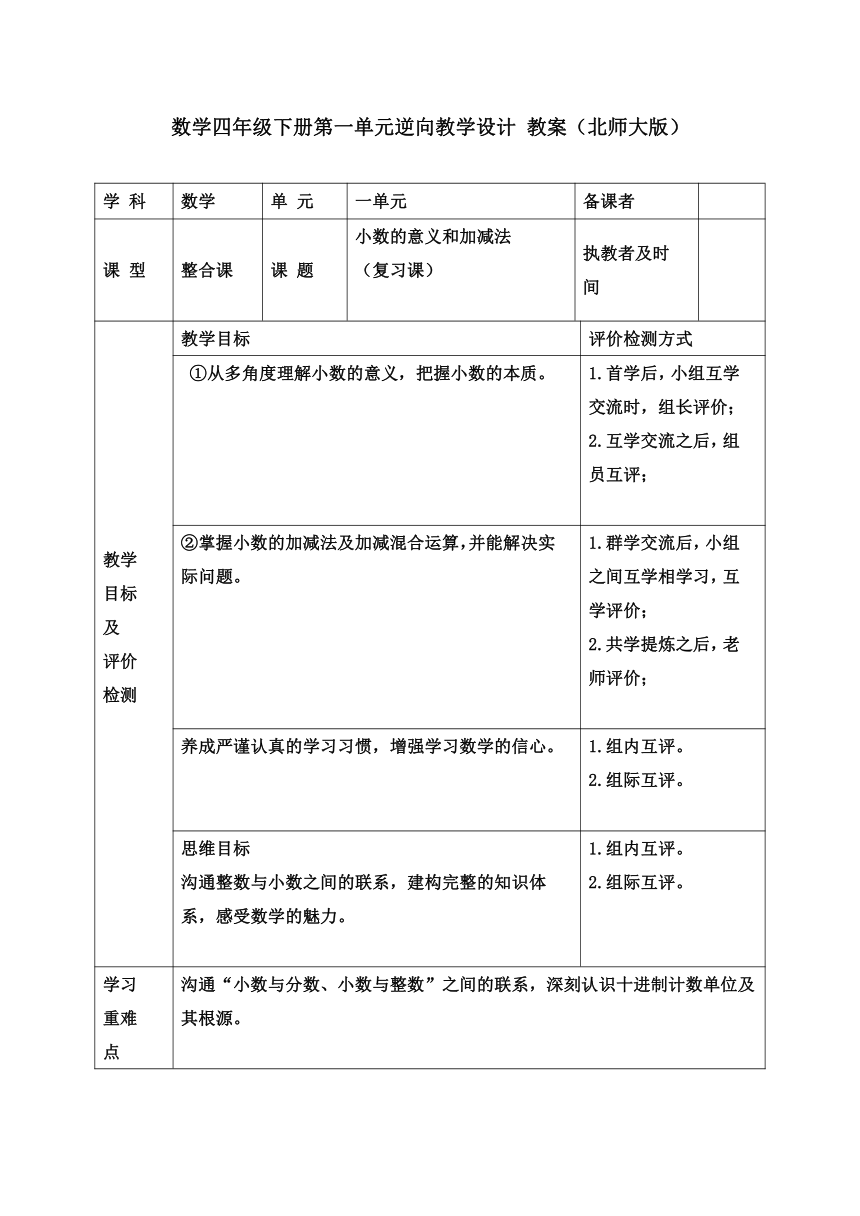
数学四年级下册第一单元逆向教学设计 教案(北师大版)
学 科 数学 单 元 一单元 备课者
课 型 整合课 课 题 小数的意义和加减法 (复习课) 执教者及时间
教学 目标 及 评价 检测 教学目标 评价检测方式
①从多角度理解小数的意义,把握小数的本质。 1.首学后,小组互学交流时,组长评价; 2.互学交流之后,组员互评;
②掌握小数的加减法及加减混合运算,并能解决实际问题。 1.群学交流后,小组之间互学相学习,互学评价; 2.共学提炼之后,老师评价;
养成严谨认真的学习习惯,增强学习数学的信心。 1.组内互评。 2.组际互评。
思维目标 沟通整数与小数之间的联系,建构完整的知识体系,感受数学的魅力。 1.组内互评。 2.组际互评。
学习 重难点 沟通“小数与分数、小数与整数”之间的联系,深刻认识十进制计数单位及其根源。
资源 运用 新世界小学数学问题 PPT
教学与学习过程 二次备课
激趣 创境 开启 探究 思维预热(导入) 请移动下面等式中的一个数字(只能是数字,不能将数字对调,也不能移动符号),使等式成立。 101---102=1
精讲 展练 开放 研讨 (1)分类再现 ①回顾小数的意义 在括号里填上合适的数 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 首学,独立完成 互学,组内交流 群学,展示成果 共学,总结提炼 整数:用“1”去量正好量完;整数是由“1”累加而成的。 分数:用“1”不能正好量完;就把“1”平均分成若干份,用其中的1份去量,其中的1份或几份可以用分数表示。 小数:用“1”不能正好量完;就把“1”平均分成10、100、1000……份,用其中的1份去量;十分之几、百分之几、千分之几……这样的分数也可以用小数表示。 ②体会小数产生的必要 第一,创设情境,体会小数产生的必要 师:(请大家看看这几幅图)既然这些数量已经可以用分数表示,为什么还要用小数来表示呢? 生:简单、方便。 第二,解决问题,沟通小数与整数的联系 师:哪种写法更简便呢?为什么? 生:我感觉小数的写法更简便些,因为写小数时不写分数线。 生:总感觉小数自然些。 师:咱们身边有这样的例子吗?(课件出示) 师:这些数都可以分数来表示,但习惯上我们用小数来表示。 师:现在,我们能感觉到:比起分数,小数好像更流畅,更直观,自然。其实小数与什么数在写法上很相近呢? 生:和整数在写法上很相近。 师:确实。小数与整数在写法上是基本一致的。它们在读、写时都是从高位起,简单,自然。 师:我们还学习了“小数加减法”和“小数乘法”,小数的计算与整数有联系吗? 我们可以这样说:小数与整数在计算上是基本一致的。
总结 提升 开创 拓展 (2)系统整理 ①走进历史,沟通联系 师:为什么整数与小数能够如此相近呢?让我们走进数学历史,或许能从中找到答案。(依次出示课件) 这样计数不方便,怎么办呢?——按群计数。我们常说的“三五成群”“屈指可数”就是这样来的。这样一块石头或一根木材可以表示更多的数量。其实咱们现在计数的方法就受到了这种思想的启发,比如:(课件出示) 师:比如,要数数这群羊有多少只?可以怎么数? 生:可以一只一只地数。 生:可以一十一十地数。 师:看看这些计数单位,熟悉吗?这就是我们常用的计数单位。我们将这些计数单位选出来。当然,也可以将它们排列在这样的表中。它们所在的位置,就是它们的—— 生:数位。 师:你瞧,这就是我们熟悉的“整数数位顺序表”!为什么我们选用这些计数单位作为整数常用的单位呢? 生:这些计数单位很方便。 生:因为这些计数单位之间的进率都是10。 师:确实,相邻计数单位间的进率都是十。这样的联系,简单、方便! 师:数量越来越多,我们可以选用更大的计数单位;数量越来越少呢?比如:1张纸片可以用“1”来表示,那这里的红色部分用哪个数来表示呢?猜猜。 生:1/3 生:1/4 ······ 师:到底是多少呢?还是得数一数。怎么数呢?用这些单位数行吗(指整数的计数单位)? 生:画格子,然后用其中的一个格子来数。 生:平均分,然后用其中的一份来数。 师:其实,你们刚才想的方法,都是为了得到更小的计数单位来数对吧?我们选几个来试试!(依次选用:1/2、1/3、1/5、1/10、1/20、1/100等“单位”数,学生选择合适的单位表示。) 为什么我们选用这些单位作为小数的计数单位呢? 师:能不能把这些计数单位填到这两张表里去。 总结:为什么整数与小数如此相近呢?因为它们的计数规则相同——都是“十进制”。正因为如此,我们把整数和小数统一起来了,把整数和这样的分数也就统一起来了。 ②操作体验,渗透思想 师:认识它吗?数轴上已经标出了0和1的位置。能告诉我,0到1之间还有数吗? 生:有。 生:有很多个。 师:你能在这条数轴上找到0.1吗?(学生在学习单上独立完成。) (展示) 师:要找到0.1先要干嘛? 生:平均分。 师:你能在这条数轴上找到0.01吗?(给你的同桌瞧瞧,找对了吗)你能在数轴上找到0.001吗?看看我能不能找到?我们从数轴上,能不能看到这三个数有什么关系呢? 师:最接近0的数是几呢?能找到0.9吗?最近1的小数是几呢? ①小数的组成。 师:现在,咱们来玩个游戏:我说你涂。你可以在学习单上选择合适的图涂一涂。 第一个:0.05。(学生独立完成) 第二个:0.6。 第三个:0.65。 师:谁来展示下你的成果,并说一说你是怎样想的? 生:(展示后)这张正方形纸片平均分成100份,我涂了其中的5份,就是0.05。这张正方形纸片平均分成10份,我涂了其中的6份,就是0.6。0.65是65个0.01,所以我选用这个正方形涂了65个格子。 师:说的很清楚。0.65还有其它的涂法吗? 生:还可以将前两个小数圈起来,就是0.65了。 师:能听明白吗?他说的是什么意思啊? 生:因为0.65是由0.6和0.05组成的,所以只需要把前面涂的圈起来就是0.65了。 师:真会动脑筋!遇到像这样的填一填,我相信难不倒大家了,不信瞧瞧。(课件演示,学生作答) ②利用小数的意义解决问题。 星期天,小明走了0.3千米,到文具店买了一块0.3元的橡皮,一共用了0.3小时。其中的“0.3千米”“0.3元”“0.3小时”各表示什么意义?
板书 设计 小数的意义和加减法(复习课) 为什么整数与小数如此相近呢?因为它们的计数规则相同——都是“十进制”。正因为如此,我们把整数和小数统一起来了,把整数和这样的分数也就统一起来了。
作业 设计 前置作业练习 在括号里填上合适的数
课中练习
课后作业设计 ①教材“练习一”中剩余的题目作为本节课的检测题目 ②我会思 这节课你有什么新的收获?
教学 后记
学 科 数学 单 元 一单元 备课者
课 型 整合课 课 题 小数的意义和加减法 (复习课) 执教者及时间
教学 目标 及 评价 检测 教学目标 评价检测方式
①从多角度理解小数的意义,把握小数的本质。 1.首学后,小组互学交流时,组长评价; 2.互学交流之后,组员互评;
②掌握小数的加减法及加减混合运算,并能解决实际问题。 1.群学交流后,小组之间互学相学习,互学评价; 2.共学提炼之后,老师评价;
养成严谨认真的学习习惯,增强学习数学的信心。 1.组内互评。 2.组际互评。
思维目标 沟通整数与小数之间的联系,建构完整的知识体系,感受数学的魅力。 1.组内互评。 2.组际互评。
学习 重难点 沟通“小数与分数、小数与整数”之间的联系,深刻认识十进制计数单位及其根源。
资源 运用 新世界小学数学问题 PPT
教学与学习过程 二次备课
激趣 创境 开启 探究 思维预热(导入) 请移动下面等式中的一个数字(只能是数字,不能将数字对调,也不能移动符号),使等式成立。 101---102=1
精讲 展练 开放 研讨 (1)分类再现 ①回顾小数的意义 在括号里填上合适的数 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 首学,独立完成 互学,组内交流 群学,展示成果 共学,总结提炼 整数:用“1”去量正好量完;整数是由“1”累加而成的。 分数:用“1”不能正好量完;就把“1”平均分成若干份,用其中的1份去量,其中的1份或几份可以用分数表示。 小数:用“1”不能正好量完;就把“1”平均分成10、100、1000……份,用其中的1份去量;十分之几、百分之几、千分之几……这样的分数也可以用小数表示。 ②体会小数产生的必要 第一,创设情境,体会小数产生的必要 师:(请大家看看这几幅图)既然这些数量已经可以用分数表示,为什么还要用小数来表示呢? 生:简单、方便。 第二,解决问题,沟通小数与整数的联系 师:哪种写法更简便呢?为什么? 生:我感觉小数的写法更简便些,因为写小数时不写分数线。 生:总感觉小数自然些。 师:咱们身边有这样的例子吗?(课件出示) 师:这些数都可以分数来表示,但习惯上我们用小数来表示。 师:现在,我们能感觉到:比起分数,小数好像更流畅,更直观,自然。其实小数与什么数在写法上很相近呢? 生:和整数在写法上很相近。 师:确实。小数与整数在写法上是基本一致的。它们在读、写时都是从高位起,简单,自然。 师:我们还学习了“小数加减法”和“小数乘法”,小数的计算与整数有联系吗? 我们可以这样说:小数与整数在计算上是基本一致的。
总结 提升 开创 拓展 (2)系统整理 ①走进历史,沟通联系 师:为什么整数与小数能够如此相近呢?让我们走进数学历史,或许能从中找到答案。(依次出示课件) 这样计数不方便,怎么办呢?——按群计数。我们常说的“三五成群”“屈指可数”就是这样来的。这样一块石头或一根木材可以表示更多的数量。其实咱们现在计数的方法就受到了这种思想的启发,比如:(课件出示) 师:比如,要数数这群羊有多少只?可以怎么数? 生:可以一只一只地数。 生:可以一十一十地数。 师:看看这些计数单位,熟悉吗?这就是我们常用的计数单位。我们将这些计数单位选出来。当然,也可以将它们排列在这样的表中。它们所在的位置,就是它们的—— 生:数位。 师:你瞧,这就是我们熟悉的“整数数位顺序表”!为什么我们选用这些计数单位作为整数常用的单位呢? 生:这些计数单位很方便。 生:因为这些计数单位之间的进率都是10。 师:确实,相邻计数单位间的进率都是十。这样的联系,简单、方便! 师:数量越来越多,我们可以选用更大的计数单位;数量越来越少呢?比如:1张纸片可以用“1”来表示,那这里的红色部分用哪个数来表示呢?猜猜。 生:1/3 生:1/4 ······ 师:到底是多少呢?还是得数一数。怎么数呢?用这些单位数行吗(指整数的计数单位)? 生:画格子,然后用其中的一个格子来数。 生:平均分,然后用其中的一份来数。 师:其实,你们刚才想的方法,都是为了得到更小的计数单位来数对吧?我们选几个来试试!(依次选用:1/2、1/3、1/5、1/10、1/20、1/100等“单位”数,学生选择合适的单位表示。) 为什么我们选用这些单位作为小数的计数单位呢? 师:能不能把这些计数单位填到这两张表里去。 总结:为什么整数与小数如此相近呢?因为它们的计数规则相同——都是“十进制”。正因为如此,我们把整数和小数统一起来了,把整数和这样的分数也就统一起来了。 ②操作体验,渗透思想 师:认识它吗?数轴上已经标出了0和1的位置。能告诉我,0到1之间还有数吗? 生:有。 生:有很多个。 师:你能在这条数轴上找到0.1吗?(学生在学习单上独立完成。) (展示) 师:要找到0.1先要干嘛? 生:平均分。 师:你能在这条数轴上找到0.01吗?(给你的同桌瞧瞧,找对了吗)你能在数轴上找到0.001吗?看看我能不能找到?我们从数轴上,能不能看到这三个数有什么关系呢? 师:最接近0的数是几呢?能找到0.9吗?最近1的小数是几呢? ①小数的组成。 师:现在,咱们来玩个游戏:我说你涂。你可以在学习单上选择合适的图涂一涂。 第一个:0.05。(学生独立完成) 第二个:0.6。 第三个:0.65。 师:谁来展示下你的成果,并说一说你是怎样想的? 生:(展示后)这张正方形纸片平均分成100份,我涂了其中的5份,就是0.05。这张正方形纸片平均分成10份,我涂了其中的6份,就是0.6。0.65是65个0.01,所以我选用这个正方形涂了65个格子。 师:说的很清楚。0.65还有其它的涂法吗? 生:还可以将前两个小数圈起来,就是0.65了。 师:能听明白吗?他说的是什么意思啊? 生:因为0.65是由0.6和0.05组成的,所以只需要把前面涂的圈起来就是0.65了。 师:真会动脑筋!遇到像这样的填一填,我相信难不倒大家了,不信瞧瞧。(课件演示,学生作答) ②利用小数的意义解决问题。 星期天,小明走了0.3千米,到文具店买了一块0.3元的橡皮,一共用了0.3小时。其中的“0.3千米”“0.3元”“0.3小时”各表示什么意义?
板书 设计 小数的意义和加减法(复习课) 为什么整数与小数如此相近呢?因为它们的计数规则相同——都是“十进制”。正因为如此,我们把整数和小数统一起来了,把整数和这样的分数也就统一起来了。
作业 设计 前置作业练习 在括号里填上合适的数
课中练习
课后作业设计 ①教材“练习一”中剩余的题目作为本节课的检测题目 ②我会思 这节课你有什么新的收获?
教学 后记
