6.3 等可能事件的概率(第1课时) 课件(共28张PPt)
文档属性
| 名称 | 6.3 等可能事件的概率(第1课时) 课件(共28张PPt) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:36:40 | ||
图片预览








文档简介
(共28张PPT)
6.3 等可能事件的概率
第1课时
1.通过摸球游戏,帮助学生了解计算一类事件发生的可能性的方法,体会概率的意义.
2.通过本节课的学习,帮助学生更容易地感受到数学与现实生活的联系,体验到数学在解决实际问题中的作用,培养学生实事求是的态度及合作交流的能力.
3.通过环环相扣、层层深入的问题设置以及分组游戏的设置,鼓励学生积极参与,培养学生自主、合作、探究的能力,培养学生学习数学的兴趣.
【教学重点】
概率的意义及其计算方法的理解与应用
【教学难点】
灵活应用概率的计算方法解决各种类型的实际问题.
一些球类比赛中裁判用抛硬币的方法来决定哪个队先开球,为什么用这种方法决定谁先开球呢?
试验1 抛掷一个质地均匀的骰子
(1)它落地时向上的点数有几种可能的结果?
(2)各点数出现的可能性会相等吗?
(3)试猜想:各点数出现的可能性大小是多少?
6种
相等
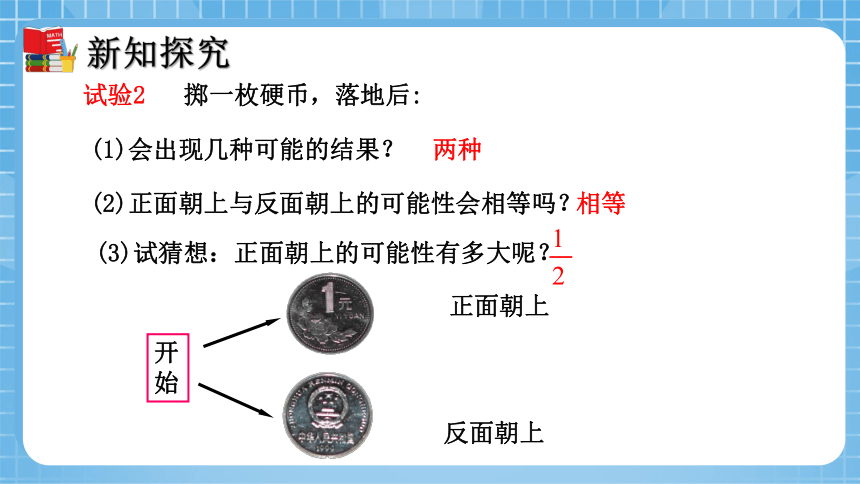
试验2 掷一枚硬币,落地后:
(1)会出现几种可能的结果?
(2)正面朝上与反面朝上的可能性会相等吗?
(3)试猜想:正面朝上的可能性有多大呢?
开始
正面朝上
反面朝上
两种
相等
试验3 一个袋中有5个球,分别标有1,2,3,4,5这5个号码,这些球除号码外都相同,搅匀后任意摸出一个球.
(1)会出现哪些可能的结果?
答:可能为摸出1,2,3,4,5号球5种结果.
(2)每个结果出现的可能性相同吗?猜一猜它们的概率分别是多少?
思考:前面我们提到的抛硬币,掷骰子和前面的摸球游戏有什么共同点?
共同点:
1.每次试验有且仅有一个结果出现;且试验的结果是有限的;
2.每个结果出现的可能性相等.
设一个试验的所有可能结果有n个,每次试验有且只有其中的一个结果出现. 如果每个结果出现的可能性相同,那么我们就称这个试验的结果是等可能的.
等可能事件A的概率计算公式
若某一等可能性随机事件的结果共有n种,那么,每一种结果出现的概率都是 。
如果等可能性事件的结果共有n个,某个事件A包含了其中的m个结果,
P(事件A)=
事件A包含的结果总数m
所有可能的结果总数n
=
切记:公式在等可能性下适用
例1.任意掷一枚均匀骰子。
(1)掷出的点数大于4的概率是多少?
(2)掷出的点数是偶数的概率是多少?
解:任意掷一枚均匀骰子,所有可能的结果有6种:掷出的点数分别是1,2,3,4,5,6,因为骰子是均匀的,所以每种结果出现的可能性相等。
(1) 掷出的点数大于4的结果只有 2 种:掷出的点数分别是 5,6,所以 P(掷出的点数大于4)
(2)掷出的点数是偶数的结果有 3 种: 掷出的点数分别是 2,4,6,所以P(掷出的点数是偶数)
方法总结:概率的求法关键是找准两点:①全部情况的总数;②符合条件的情况数目.二者的比值就是其发生的概率.
例2 有7张卡片,分别写有-1,0,1,2,3,4,5这7个数字,从中任意抽取一张.
(1)求抽到的数字为正数的概率.
(2)求抽到数字的绝对值小于2的概率.
分析:(1)先找出分别标有数字-1,0,1,2,3,4,5的7张卡片中正数的个数,再根据概率公式解答.
(2)先找出分别标有数字-1,0,1,2,3,4,5的7张卡片中绝对值小于2的个数,再根据概率公式解答.
解:(1)在7张卡片中,正数有1,2,3,4,5这5个,
故P(抽到正数的卡片)= .
(2)在7张卡片中,绝对值小于2的有-1,0,1这3个,
故P(抽到绝对值小于2的卡片)= .
例2 有7张卡片,分别写有-1,0,1,2,3,4,5这7个数字,从中任意抽取一张.
(1)求抽到的数字为正数的概率.
(2)求抽到数字的绝对值小于2的概率.
判断事件A是否为等可能事件;
计算所有事件的总结果数n;
计算事件A包含的结果数m;
利用公式计算
求等可能事件A发生的概率的步骤
归纳总结
1.下列说法中,正确的是( )
A.不可能事件发生的概率为0
B.随机事件发生的概率为
C.概率很小的事件不可能发生
D.投掷一枚质地均匀的硬币100次,正面朝上的次数一定为50次
2.甲、乙、丙、丁四名选手参加100米决赛,赛场只设1,2,3,4四个跑道,选手以随机抽签的方式决定各自的跑道,若甲首先抽签,则甲抽到1号跑道的概率是 ( )
A.1 B. C. D.
D
3.在一个不透明的口袋中装有5个完全相同的小球,它们分别标有1,2,3,4,5,从中随机摸出一个小球,其标号是奇数的概率为( )
A. B.
C. D.
4. 如图,在4×4的正方形网格中,黑色部分的图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是( )
A. B.
C. D.
B
5.一只蚂蚁在如图所示的树枝上寻觅食物,假定蚂蚁在每个岔路口都随机选择一条路径,则它获得食物的概率是( )
C
6.一个桶里有60个弹珠——一些是红色的,一些是蓝色的,一些是白色的.拿出红色弹珠的概率是35%,拿出蓝色弹珠的概率是25%.桶里每种颜色的弹珠各有多少?
7.我市将面向全市中小学开展“经典诵读”比赛.某中学要从2名男生、2名女生共4名学生中选派2名学生参赛.
(1)请列举所有可能出现的选派结果;
解:记4名学生分别为男1,男2,女1,女2,则所有可能出现的结果为:男1男2,男1女1,男1女2,男2女1,男2女2,女1女2.
7.我市将面向全市中小学开展“经典诵读”比赛.某中学要从2名男生、2名女生共4名学生中选派2名学生参赛.
(2)求选派的2名学生中,恰好为1名男生、1名女生的概率.
8.有7张纸签,分别标有数字1,1,2,2,3,4,5,从中随机地抽出一张,求:
(1)抽出标有数字3的纸签的概率;
(2)抽出标有数字1的纸签的概率;
(3)抽出标有数字为奇数的纸签的概率.
解:(1)P(数字3)=
(2)P(数字1)=
(3)P(数字为奇数)=
9. 掷一个骰子,观察向上的一面的点数,求下列事件的概率:
(1)点数为2;
(2)点数为奇数;
(3)点数大于2小于5.
解:(1)点数为2有1种可能,因此P(点数为2)= ;
(2)点数为奇数有3种可能,即点数为1,3,5,因此P(点数为奇数)= ;
(3)点数大于2且小于5有2种可能,即点数为3,4,因此 P(点数大于2且小于5)= .
1.频率的稳定性.
2.事件A的概率,记为P(A).
3.一般的,大量重复的实验中,我们常用不确定事件 A 发生的频率来估计事件A发生的概率.
4.必然事件发生的概率为1;
不可能事件发生的概率为0;
随机事件 A 发生的概率P(A)是0与1之间的一个常数.
应用 求简单事件的概率的步骤:
(3)计算:套入公式 计算
(1)判断:试验所有可能出现的结果必须是有限的,各种结果出现的可能性必须相等;
(2)确定:试验发生的所有的结果数n和事件A发生
的所有结果数m;
习题6.4
第1、2、3题
6.3 等可能事件的概率
第1课时
1.通过摸球游戏,帮助学生了解计算一类事件发生的可能性的方法,体会概率的意义.
2.通过本节课的学习,帮助学生更容易地感受到数学与现实生活的联系,体验到数学在解决实际问题中的作用,培养学生实事求是的态度及合作交流的能力.
3.通过环环相扣、层层深入的问题设置以及分组游戏的设置,鼓励学生积极参与,培养学生自主、合作、探究的能力,培养学生学习数学的兴趣.
【教学重点】
概率的意义及其计算方法的理解与应用
【教学难点】
灵活应用概率的计算方法解决各种类型的实际问题.
一些球类比赛中裁判用抛硬币的方法来决定哪个队先开球,为什么用这种方法决定谁先开球呢?
试验1 抛掷一个质地均匀的骰子
(1)它落地时向上的点数有几种可能的结果?
(2)各点数出现的可能性会相等吗?
(3)试猜想:各点数出现的可能性大小是多少?
6种
相等
试验2 掷一枚硬币,落地后:
(1)会出现几种可能的结果?
(2)正面朝上与反面朝上的可能性会相等吗?
(3)试猜想:正面朝上的可能性有多大呢?
开始
正面朝上
反面朝上
两种
相等
试验3 一个袋中有5个球,分别标有1,2,3,4,5这5个号码,这些球除号码外都相同,搅匀后任意摸出一个球.
(1)会出现哪些可能的结果?
答:可能为摸出1,2,3,4,5号球5种结果.
(2)每个结果出现的可能性相同吗?猜一猜它们的概率分别是多少?
思考:前面我们提到的抛硬币,掷骰子和前面的摸球游戏有什么共同点?
共同点:
1.每次试验有且仅有一个结果出现;且试验的结果是有限的;
2.每个结果出现的可能性相等.
设一个试验的所有可能结果有n个,每次试验有且只有其中的一个结果出现. 如果每个结果出现的可能性相同,那么我们就称这个试验的结果是等可能的.
等可能事件A的概率计算公式
若某一等可能性随机事件的结果共有n种,那么,每一种结果出现的概率都是 。
如果等可能性事件的结果共有n个,某个事件A包含了其中的m个结果,
P(事件A)=
事件A包含的结果总数m
所有可能的结果总数n
=
切记:公式在等可能性下适用
例1.任意掷一枚均匀骰子。
(1)掷出的点数大于4的概率是多少?
(2)掷出的点数是偶数的概率是多少?
解:任意掷一枚均匀骰子,所有可能的结果有6种:掷出的点数分别是1,2,3,4,5,6,因为骰子是均匀的,所以每种结果出现的可能性相等。
(1) 掷出的点数大于4的结果只有 2 种:掷出的点数分别是 5,6,所以 P(掷出的点数大于4)
(2)掷出的点数是偶数的结果有 3 种: 掷出的点数分别是 2,4,6,所以P(掷出的点数是偶数)
方法总结:概率的求法关键是找准两点:①全部情况的总数;②符合条件的情况数目.二者的比值就是其发生的概率.
例2 有7张卡片,分别写有-1,0,1,2,3,4,5这7个数字,从中任意抽取一张.
(1)求抽到的数字为正数的概率.
(2)求抽到数字的绝对值小于2的概率.
分析:(1)先找出分别标有数字-1,0,1,2,3,4,5的7张卡片中正数的个数,再根据概率公式解答.
(2)先找出分别标有数字-1,0,1,2,3,4,5的7张卡片中绝对值小于2的个数,再根据概率公式解答.
解:(1)在7张卡片中,正数有1,2,3,4,5这5个,
故P(抽到正数的卡片)= .
(2)在7张卡片中,绝对值小于2的有-1,0,1这3个,
故P(抽到绝对值小于2的卡片)= .
例2 有7张卡片,分别写有-1,0,1,2,3,4,5这7个数字,从中任意抽取一张.
(1)求抽到的数字为正数的概率.
(2)求抽到数字的绝对值小于2的概率.
判断事件A是否为等可能事件;
计算所有事件的总结果数n;
计算事件A包含的结果数m;
利用公式计算
求等可能事件A发生的概率的步骤
归纳总结
1.下列说法中,正确的是( )
A.不可能事件发生的概率为0
B.随机事件发生的概率为
C.概率很小的事件不可能发生
D.投掷一枚质地均匀的硬币100次,正面朝上的次数一定为50次
2.甲、乙、丙、丁四名选手参加100米决赛,赛场只设1,2,3,4四个跑道,选手以随机抽签的方式决定各自的跑道,若甲首先抽签,则甲抽到1号跑道的概率是 ( )
A.1 B. C. D.
D
3.在一个不透明的口袋中装有5个完全相同的小球,它们分别标有1,2,3,4,5,从中随机摸出一个小球,其标号是奇数的概率为( )
A. B.
C. D.
4. 如图,在4×4的正方形网格中,黑色部分的图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是( )
A. B.
C. D.
B
5.一只蚂蚁在如图所示的树枝上寻觅食物,假定蚂蚁在每个岔路口都随机选择一条路径,则它获得食物的概率是( )
C
6.一个桶里有60个弹珠——一些是红色的,一些是蓝色的,一些是白色的.拿出红色弹珠的概率是35%,拿出蓝色弹珠的概率是25%.桶里每种颜色的弹珠各有多少?
7.我市将面向全市中小学开展“经典诵读”比赛.某中学要从2名男生、2名女生共4名学生中选派2名学生参赛.
(1)请列举所有可能出现的选派结果;
解:记4名学生分别为男1,男2,女1,女2,则所有可能出现的结果为:男1男2,男1女1,男1女2,男2女1,男2女2,女1女2.
7.我市将面向全市中小学开展“经典诵读”比赛.某中学要从2名男生、2名女生共4名学生中选派2名学生参赛.
(2)求选派的2名学生中,恰好为1名男生、1名女生的概率.
8.有7张纸签,分别标有数字1,1,2,2,3,4,5,从中随机地抽出一张,求:
(1)抽出标有数字3的纸签的概率;
(2)抽出标有数字1的纸签的概率;
(3)抽出标有数字为奇数的纸签的概率.
解:(1)P(数字3)=
(2)P(数字1)=
(3)P(数字为奇数)=
9. 掷一个骰子,观察向上的一面的点数,求下列事件的概率:
(1)点数为2;
(2)点数为奇数;
(3)点数大于2小于5.
解:(1)点数为2有1种可能,因此P(点数为2)= ;
(2)点数为奇数有3种可能,即点数为1,3,5,因此P(点数为奇数)= ;
(3)点数大于2且小于5有2种可能,即点数为3,4,因此 P(点数大于2且小于5)= .
1.频率的稳定性.
2.事件A的概率,记为P(A).
3.一般的,大量重复的实验中,我们常用不确定事件 A 发生的频率来估计事件A发生的概率.
4.必然事件发生的概率为1;
不可能事件发生的概率为0;
随机事件 A 发生的概率P(A)是0与1之间的一个常数.
应用 求简单事件的概率的步骤:
(3)计算:套入公式 计算
(1)判断:试验所有可能出现的结果必须是有限的,各种结果出现的可能性必须相等;
(2)确定:试验发生的所有的结果数n和事件A发生
的所有结果数m;
习题6.4
第1、2、3题
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
