2023-2024学年江苏省南京市第一中学江北新区分校八年级上学期10月月考数学试卷(PDF版 含解析)
文档属性
| 名称 | 2023-2024学年江苏省南京市第一中学江北新区分校八年级上学期10月月考数学试卷(PDF版 含解析) |  | |
| 格式 | |||
| 文件大小 | 662.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-09 19:21:24 | ||
图片预览

文档简介
2023-2024 学年江苏省南京市第一中学江北新区分校八年级
上学期 10 月月考数学试卷
一、单选题
1.中国“二十四节气”已被列入联合国教科文组织人类非物质文化遗产代表作名录,下
列四幅作品分别代 表“大雪”、“白露”、“芒种”、“立春”,其中是轴对称图形的是( )
A. B. C. D.
2.如图,若△ABC≌△DEF,且 AB 5,AC 6,BC 7,则 EF 的长为( )
A.5 B.6 C.7 D.8
3.如图,要测量池塘两岸相对的两点 A,B的距离,小明在池塘外取 AB的垂线 BF上
的点 C,D,使 BC CD,再画出 BF的垂线DE,使 E与 A,C在一条直线上,这时测
得DE的长就是 AB的长,依据是( )
A.SSS B.SAS C.ASA D.HL
4.在联欢会上,有 A、B、C三名选手站在一个三角形的三个顶点位置上,他们在玩“抢
凳子”游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳
子应放的最适当的位置是在 ABC的( )
A.三边垂直平分线的交点 B.三条中线的交点
C.三条角平分线的交点 D.三条高所在直线的交点
5.如图,在 ABC中, BAC=110 ,EF 是边 AB的垂直平分线,垂足为 E,交 BC于
F.MN是边 AC的垂直平分线,垂足为 M,交 BC于 N.连接 AF、 AN则 FAN 的度
数是( )
试卷第 1页,共 7页
A.70 B.55 C.40 D.30
6.如图,在 ABC中, C 90 , B 30 ,以 A为圆心,任意长为半径两弧分别交
1
AB、AC于点 M和 N,再分别以 M、N为圆心,大于 MN的长为半径画弧,两弧交于
2
点 P,连接 AP并延长交 BC于点 D,则下列说法中正确的个数是( )
① AD是 BAC的平分线;② ADC 60 ;③点 D在 AB的垂直平分线上;
④ S△DAC : S△ABD 1: 3.
A.4 B.3 C.2 D.1
7.如图,四边形 ABCD中, AB AD,点 B关于 AC的对称点 B 恰好落在CD上,若
BAD ,则 ACB的度数为( )
1
A. 45 B. 45 C. D.90
1
2 2
8.如果正整数 a、b、 c满足符式 a2 b2 c2,那么正整数、b、c叫做勾股数,某同
学将自己探究勾股数的过程列成下表,观察表中每列数的规律,可知 x y的值为( )
a b c
3 4 5
8 6 10
15 8 17
试卷第 2页,共 7页
24 10 26
x y 65
A. 47 B.62 C.79 D.98
二、填空题
9.在平面镜里看到背后墙上,电子钟示数如图所示,这时的时间应是 .
10.直角三角形两边长为 6和 8,则斜边中线长为 .
11.如图,在Rt△ABC中, C 90 ,AD平分 BAC,交 BC于点 D.DE AB于 E.若
BC 5, BD 3,则DE的长为 .
12.如图,在 ABC中, AD平分 BAC, AD BD于点 D,且 S ABC 10,则 ADC的
面积为 .
13.如图, ABC是等边三角形.D,E分别是 AC,BC上的点,若
AE AD, CED 20 .则 BAE .
试卷第 3页,共 7页
14.如图Rt△ABC中, C 90 ,分别以三角形各边为直径作半圆,图中阴影部分在
数学史上称为“希波克拉底月牙”;当 AC 3,BC 4时,阴影部分的面积为 .
15.在△ABC中,∠A=80°,当∠B= 时,△ABC是等腰三角形.
16.如图,∠AOB=45°,点M、N分别在射线 OA、OB上,MN=7,△OMN的面积为
14,P是直线MN上的动点,点 P关于 OA对称的点为 P1,点 P关于 OB对称点为 P2,
当点 P在直线 NM上运动时,△OP1P2的面积最小值为
三、解答题
17.如图,点 A、C、F、D在同一直线上, AF DC , A D ,AB DE .求证:
△ABC≌△DEF.
试卷第 4页,共 7页
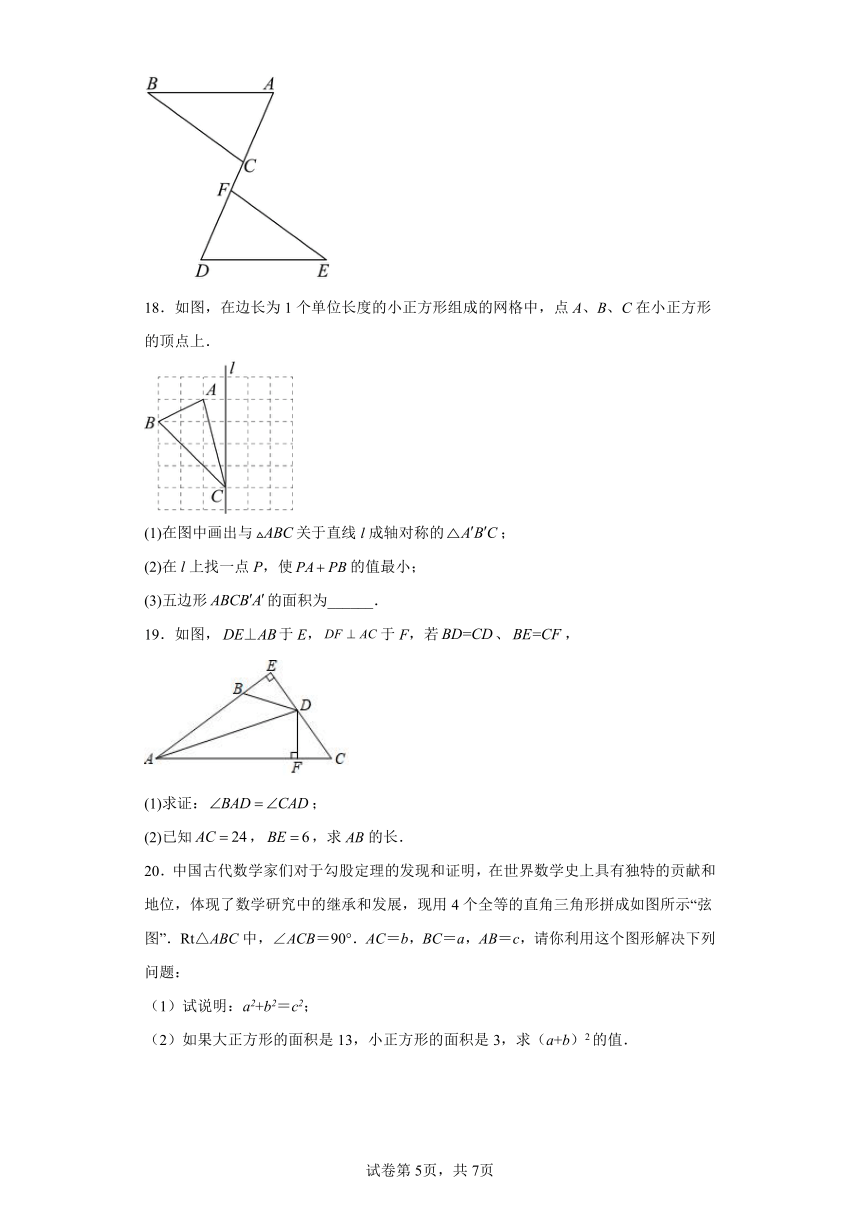
18.如图,在边长为 1个单位长度的小正方形组成的网格中,点 A、B、C在小正方形
的顶点上.
(1)在图中画出与 ABC关于直线 l成轴对称的△A B C;
(2)在 l上找一点 P,使 PA PB的值最小;
(3)五边形 ABCB A 的面积为______.
19.如图,DE⊥AB于 E,DF AC于 F,若 BD=CD、 BE=CF,
(1)求证: BAD CAD;
(2)已知 AC 24, BE 6,求 AB的长.
20.中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和
地位,体现了数学研究中的继承和发展,现用 4个全等的直角三角形拼成如图所示“弦
图”.Rt△ABC中,∠ACB=90°.AC=b,BC=a,AB=c,请你利用这个图形解决下列
问题:
(1)试说明:a2+b2=c2;
(2)如果大正方形的面积是 13,小正方形的面积是 3,求(a+b)2的值.
试卷第 5页,共 7页
21.如图, AD,BE是 ABC的高线. AD与 BE相交于点 F,若 AD BD 6,且 ACD
的面积为 12,求线段 AF的长度.
22.如图所示,长方形纸片 ABCD的长 AD=8cm,宽 AB=4cm,将其沿着折痕 EF折
叠,使点 D与点 B重合.
(1)求证:BE=BF;
(2)求折叠后△BEF的面积.
23.已知线段 a和b.
(1)用直尺和圆规作等腰 ABC,使得 AB AC,BC a,BC边上的高 AD = b(保留作
图痕迹,不写作法);
(2)用直尺和圆规作等腰 ABC,使得 AB AC b, BC边上的高 AD a(保留作图痕
迹,不写作法).
24.【问题提出】
(1)如图 1,锐角 ABC中分别以 AB、AC为边向外作等腰 ABE和等腰 ACD,使
AE AB,AD AC, BAE CAD,连接 BD、CE,试猜想 BD与CE的数量关系,
试卷第 6页,共 7页
并说明理由;
AI
【探索研究】
(2)如图 2,在 ABC中, ACB 45 ,以 AB为直角边,点 A为直角顶点向外作等
腰直角△ABD,连接CD,若 AC 2,BC 4,求CD的长;
【解决问题】
(3)如图 3,在四边形 ABCD中, ADC 60 ,BC 13,AB 6,AD CD,则 BD的
最大值为_____.
试卷第 7页,共 7页
参考答案:
1.A
【分析】本题考查了轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对
称轴折叠后可重合.根据轴对称图形的知识求解.
【详解】解:A、是轴对称图形,故本选项符合题意;
B、不是轴对称图形,故本选项不符合题意;
C、不是轴对称图形,故本选项不符合题意;
D、不是轴对称图形,故本选项不符合题意.
故选:A.
2.C
【分析】本题主要考查了全等三角形的性质,根据全等三角形对应边相等即可得到
EF BC 7.
【详解】解:∵△ABC≌△DEF,BC 7,
∴EF BC 7,
故选 C.
3.C
【分析】本题主要考查了全等三角形的性质与判定,熟知全等三角形的判定定理是解题的关
键,全等三角形的判定定理有SSS,SAS,AAS,ASA,HL.
【详解】解:∵ AB⊥BF,DE⊥BF ,
∴ ABC EDC 90 ,
在 ABC和△EDC中,
ABC EDC
BC DC ,
ACB ECD
∴△ABC≌△EDC ASA ,
∴ AB DE ,
∴依据是ASA,
故选 C.
4.A
【分析】本题考查了线段垂直平分线的性质,熟练掌握线段垂直平分线上的到线段两端的距
答案第 1页,共 14页
离相等是解答本题的关键.根据线段垂直平分线的性质解答即可.
【详解】解:根据题意得:当木凳所在位置到 A、B、C三个顶点的距离相等时,游戏公平,
∵线段垂直平分线上的到线段两端的距离相等,
∴凳子应放的最适当的位置是在 ABC的三边垂直平分线的交点.
故选:A.
5.C
【分析】根据垂直平分线的性质得 AF BF, AN CN ,再由等边对等角,以及三角形内
角和定理求出所求角度数即可.
【详解】解:∵ EF 是边 AB的垂直平分线,MN是边 AC的垂直平分线,
∴ AF BF, AN CN ,
∴ BAF B, CAN C,
∵ BAC=110 ,
∴ B C 70 ,
∴ BAF CAN 70 ,
∴ FAN BAC BAF CAN 110 70 40 .
故选:C.
【点睛】此题考查了线段垂直平分线的性质,等腰三角形的性质,熟练掌握性质是解本题的
关键.线段垂直平分线上任意一点,到线段两端点的距离相等.
6.B
【分析】利用基本作图方法可对①进行判断;利用角平分线的定义计算出
BAD CAD 30 ,则由三角形内角和定理求出 ADC的度数,于是可对②进行判断;由
∠BAD ∠B得到DA DB,则根据线段垂直平分线的性质定理的逆定理可对③进行判断;
利用含30度的直角三角形三边的关系得到 AD 2CD,则 BD 2CD,然后根据三角形面积
公式可对④进行判断.
【详解】解:由作图方法可知 AD平分 BAC, 故①正确;
∵ C 90 , CAB 60 ,
∴ B 90 60 30 , BAD CAD 30 ,
∴ ADC 90 30 60 ,故②正确;
∵ B BAD 30 ,
∴ AD BD
答案第 2页,共 14页
∴点D在 AB的垂直平分线上,故③正确;
∵ CAD 30
∵ AD 2CD, C 90
∴BD AD 2CD,
∴BC 3CD,
S△DAC :S△ABD 1: 2,故④错误.
∴正确的有 3个,
故选 B.
【点睛】本题主要考查了角平分线的定义,角平分线的尺规作图,三角形内角和定理,等角
对等边,线段垂直平分线的判定,含 30度角的直角三角形的性质,熟练掌握各部分知识并
综合应用是解题的关键.
7.D
【分析】连接 AB , BB ,过 A作 AE⊥CD于 E,依据∠BAC= B AC,∠DAE= B AE,
1
即可得出∠CAE= ∠BAD,再根据四边形内角和以及三角形外角性质,即可得到∠ACB=
2
ACB 1=90° ∠BAD.
2
【详解】解:如图,连接 AB ,BB ,过 A作 AE⊥CD于 E,
∵点 B关于 AC的对称点 B 恰好落在 CD上,
∴AC垂直平分BB ,
∴AB= AB ,
∴∠BAC=∠ B AC,
∵AB=AD,
∴AD= AB ,
又∵AE⊥CD,
∴∠DAE=∠ B AE,
答案第 3页,共 14页
1 1
∴∠CAE= ∠BAD= α,
2 2
又∵ AEB = AOB =90°,
1
∴四边形 AOB E中, EB O=180° α,
2
1 1
∴ ACB = EB O COB =180° α 90°=90° α,
2 2
1
∴∠ACB= ACB =90° α,
2
故选:D.
【点睛】本题主要考查了轴对称的性质,四边形内角和以及三角形外角性质的运用,解决问
题的关键是作辅助线构造四边形 AOB E,解题时注意:如果两个图形关于某直线对称,那么
对称轴是任何一对对应点所连线段的垂直平分线.
8.C
【分析】依据每列数的规律,即可得到 a 2n,b n2 1,c n2 1,进而得出 x y的值.
【详解】解:由题可得,3 22 1,4 2 2,5 22 1,
a 2n,b n2 1,c n2 1,( n 2且 n为正整数)
当 c n2 1 65时,
解得: n 8,
x 16, y 63,
x y 79,
故选:C.
【点睛】本题主要考查了勾股数,满足 a2 b2 c2的三个正整数,称为勾股数.
9.10 : 51
【分析】在平面镜中的像与现实中的事物恰好顺序颠倒,且关于镜面对称,由此可解.
【详解】解:题中所给的“12 : 01”与“10 : 51”成轴对称,这时的时间应是10 : 51.
故答案为:10 : 51.
【点睛】本题考查镜面反射的原理与性质,解题的关键是掌握轴对称的性质.
10.5或 4/4或 5
【分析】根据两种情况:6和 8都为直角边;8为斜边,6为直角边,得到斜边长度,再利
用直角三角形斜边上的中线等于斜边的一半,即可解答.
【详解】解:当 6和 8都为直角三角形的直角边时,
答案第 4页,共 14页
根据勾股定理可得,直角三角形的斜边为 62 82 10,
斜边上的中线长为10 2 5;
当 8为直角三角形的斜边,6为直角三角形的直角边时,
斜边上的中线长为8 2 4,
综上所述,斜边中线长为 5或 4,
故答案为:5或 4.
【点睛】本题考查了勾股定理,直角三角形斜边上的中线等于斜边的一半,根据情况能够正
确地分类讨论是解题地关键.
11.2
【分析】本题考查了角平分线的性质,根据角平分线的性质得出DE CD即可求解.
【详解】解:∵ AD平分 BAC, AC CD,DE AB,
∴CD DE,
∵BC 5,BD 3,
∴CD DE 5 3 2,
故答案为:2.
12.5
【分析】延长 BD交 AC于 E,证明 ABD≌ AED ASA ,利用三角形的中线平分三角形的
面积和全等三角形的面积相等,即可得解.
【详解】解:如图,延长BD交 AC于 E,
∵ AD平分 BAC,
∴ BAD CAD,
在△ABD和△AED中,
BAD CAD
AD AD
ADB ADE
答案第 5页,共 14页
∴ ABD≌ AED ASA ,
∴BD DE,
∴ S ABD S AED, S BDC S CDE ,
∴ S ADC S
1
CDE S ADE S2 ABC
5,
故答案为:5.
【点睛】本题考查全等三角形的判定和性质,以及三角形的中线平分三角形的面积.遇到角
平分线和垂线,常常构造等腰三角形来进行解题.通过构造等腰三角形证明三角形全等是解
题的关键.
13. 40
【分析】利用等边三角形的性质可得 C BAC 60 ,从而利用三角形的外角性质可得
ADE 80 ,然后利用等腰三角形的性质可得 AED ADE 80 ,从而利用三角形的内
角和定理可得 DAE 20 ,最后利用角的和差关系进行计算即可解答.
【详解】解:∵ ABC是等边三角形,
∴ C BAC 60 ,
∵ CED 20 ,
∴ ADE CED C 80 ,
∵ AE AD,
∴ AED ADE 80 ,
∴ DAE 180 AED ADE 20 ,
∴ BAE BAC DAE 60 20 40 ,
故答案为:40.
【点睛】本题考查了等边三角形的性质,三角形外角的性质,等腰三角形的性质,三角形内
角和定理,熟练掌握等边三角形的性质是解题的关键.
14.6
【分析】本题主要考查了求不规则图形的面积,勾股定理,根据勾股定理求得 AB的长度,
再根据圆的面积公式分别计算三个半圆的面积,最后根据阴影部分的面积等于两个较小半圆
的面积和减去以 AB为直径的半圆的面积,之后再加上 ABC的面积进行求解即可.
【详解】解:∵在Rt△ABC中, ACB 90 , AC 3, BC 4,
答案第 6页,共 14页
∴AB AC2 BC2 32 42 5,
3 2
以 AC为直径得到半圆的面积: 2 9 ;
2 8
4 2
以BC 为直径半圆的面积: 2 ; 2
2
5
2
以 AB 为直径半圆的面积: 2 25 ;
2 8
1 1
Rt△ABC的面积为: AC BC 3 4 6,
2 2
∴阴影部分的面积 S半圆AC S半圆BC S半圆AB S△ABC
9 2 25 6 6 .
8 8
故答案为:6.
15.20°或 50°或 80°
【分析】分三种情况分析, A是顶角, B是顶角, C是顶角,
【详解】∵ A 80 ,
∴①当 C是顶角, B A 80 时,△ABC是等腰三角形;
②当 A是顶角,∠B=(180°﹣80°)÷2=50°时,△ABC是等腰三角形;
③ B是顶角,∠B=180°﹣80°×2=20°时,△ABC是等腰三角形;
故答案为:80°或 50°或 20°
16.8
【分析】连接 OP,过点 O作 OH NM交 NM的延长线于 H,首先利用三角形的面积公式
求出 OH,再证明△OP1P2是等腰直角三角形,当 OP最小时,△OP1P2的面积最小.
【详解】解:如图所示,连接 OP,过点 O作 OH NM交 NM的延长线于 H,
答案第 7页,共 14页
∵S
1
△OMN= MN OH=14,且MN=7,,∴OH=4,2
∵点 P关于 OA对称的点为 P1,点 P关于 OB对称点为 P2,
∴ AOP= AOP1, BOP= BOP2,OP=OP1=OP2,
∵∠AOB=45°,
∴ P1OP2=2( POA+ POB)=90 ,
∴△OP1P2是等腰直角三角形,
∴当OP=OP1最小时,△OP1P2的面积最小,
根据垂线段最短可知,OP的最小值为 4,
1
∴△OP1P2的面积的最小值= 4 4=8,2
故答案为:8.
【点睛】本题主要考查了角平分线的应用及垂线段最短的公理,解题的关键在于证明△OP1P2
是等腰直角三角形,找到 OP的最小值.
17.见解析
【分析】由 AF CD,可求得 AC DF,利用SAS可得出结论.
【详解】解: AF CD,
∴AF FC CD FC,即 AC DF,
AB DE
在 ABC和 DEF中, A D ,
AC DF
∴△ABC≌△DEF (SAS) .
【点睛】本题主要考查全等三角形的判定,掌握全等三角形的判定方法是解题的关键.
18.(1)见解析
(2)见解析
(3)13
【分析】本题考查了轴对称-最短路线问题,作图-轴对称变换.
(1)根据题意作出点 A,点 B关于 l的对称点 A 、 B ,连结CA , A B , B C即可;
(2)通过轴对称的性质,作出图形即可;
答案第 8页,共 14页
(3)割补法利用矩形面积减去 4个直角三角形面积求解即可得到结论.
【详解】(1)作出点 A,点 B关于 l的对称点 A 、 B ,连结CA , A B ,B C,
如图所示,△A B C即为所求;
(2)∵点 B与点 B 关于 l对称,
连接 AB 交直线 l与点 P,
∴PB PB ,
∴PA PB PA PB ,
则PA PB长的最短值 AB .
1 1 1 1
(3)五边形 ABCB A 的面积 6 4 1 2 1 2 3 3 3 3 13 ,
2 2 2 2
故答案为:13
19.(1)见解析
(2)12
【分析】(1)由题所给条件可得△BED≌△CFD,即得DE=DF,则 EAD CAD.
(2)由(1)问所得条件证得△ADE≌△ADF,得 AE AF 24 6 18,则
AB AE BE 18 6 12.
【详解】(1)证明:∵DE⊥AB, DF AC,
∴ E= DFC=90 ,
在Rt△BED和 RtVCFD中,
答案第 9页,共 14页
BD=CD
BE=CF
,
∴Rt BED≌Rt CFD HL ,
∴DE=DF,
∵DE⊥AB,DF AC,
∴AD平分 BAC,
∴ BAD CAD;
(2)解:∵ BAD CAD, E AFD,DE=DF,
∴△ADE≌△ADF AAS ,
∴ AE=AF,CF BE 6,
∵ AC 24,
∴ AE AF 24 6 18,
∴ AB AE BE 18 6 12.
【点睛】本题考查了全等三角形的性质和判定的应用,注意:全等三角形的判定定理有 SAS,
ASA,AAS,SSS,全等三角形的对应边相等,对应角相等.
20.(1)证明见解析;(2)23
【分析】(1)根据题意,我们可在图中找等量关系,由中间的小正方形的面积等于大正方形
的面积减去四个直角三角形的面积,列出等式化简即可得出勾股定理的表达式.
(2)根据完全平方公式的变形解答即可.
【详解】解:(1 1)∵大正方形面积为 c2,直角三角形面积为 2 ab,小正方形面积为(b﹣a)
2,
∴c2=4× 12 ab+(a﹣b)
2=2ab+a2﹣2ab+b2即 c2=a2+b2;
(2)由图可知:
(b a 1﹣ )2=3,4× 2 ab=13﹣3=10,
∴2ab=10,
∴(a+b)2=(b﹣a)2+4ab=3+2×10=23.
【点睛】本题考查了对勾股定理的证明和以及非负数的性质,掌握三角形和正方形面积计算
公式是解决问题的关键.
答案第 10页,共 14页
21.2
【分析】本题主要考查了全等三角形的判定与性质,三角形的面积等知识,利用ASA证明
△ACD≌△BFD ,得DF DC,再根据三角形面积可得CD的长,从而可得答案.
【详解】解:∵ AD, BE是 ABC的高线,
∴ ADB ADC AEB 90 ,
∵ BFD AFE,
∴ DBF CAD,
在 ACD和△BFD中,
CAD DBF
BD AD ,
BDF ADC
∴ ACD≌ BFD ASA ,
∴DF DC,
∵ ACD的面积为 12,
1
∴ CD 6 12,
2
∴CD 4,
∴DF 4,
∴ AF AD DF 2.
22.(1)证明见解析;(2)10
【分析】(1)根据轴对称的性质,得∠BEF=∠DEF;根据长方形和平行线性质,得∠BFE
=∠DEF,从而得∠BFE=∠BEF,结合等腰三角形性质,即可完成证明;
(2)结合题意设 AE=x,则 BE=DE=8﹣x;根据勾股定理的性质,通过列方程并求解,
即可得到 AE;再结合三角形的性质计算,即可得到答案.
【详解】(1)由折叠的性质得:∠BEF=∠DEF,
∵AD // BC,
∴∠BFE=∠DEF,
∴∠BFE=∠BEF,
∴BE=BF;
(2)设 AE=x,则 BE=DE=8﹣x,
答案第 11页,共 14页
在 Rt△ABE中,由勾股定理得:x2+42=(8﹣x)2
解得,x=3,
∴BE=BF=5,
∴△BEF 1 1的面积= 2 ×BF×AB= 2 ×5×4=10.
【点睛】本题考查了轴对称、矩形、平行线、等腰三角形、一元一次方程、勾股定理的知识;
解题的关键是熟练掌握矩形、轴对称、勾股定理的性质,从而完成求解.
23.(1)作图见详解
(2)作图见详解
【分析】(1)先作 BC a,再作BC的垂直平分线交 BC于D点,接着在BC的垂直平分线
上截取DA b,然后连接 AB、 AC得到 ABC;
(2)先过直线 l上的点D作直线 l的垂线,再在垂线上截取DA a,然后以点A为圆心,b
为半径画弧,分别交直线 l于点 B、C,连接 AB、 AC, ABC满足条件.
【详解】(1)解:如图 1,
ABC为所要求图形.
(2)解:如图 2,
ABC为所要求图形.
答案第 12页,共 14页
【点睛】本题考查了作图—复杂作图,等腰三角形的判断与性质.解决此类题目的关键是熟
悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.
24.(1)猜想 BD CE,理由见解析;(2) 2 5;(3)19
【分析】(1)首先根据等式的性质证明 EAC BAD,则根据SAS即可证明
△EAC≌△BAD,根据全等三角形的性质即可证明.
(2)在 AC的上方作等腰直角△ACE,使得 CAE 90 , AC AE,连接 BE,由勾股定
理可求 BE的长,由“SAS ”可证△ABE≌△ADC ,得出CD BE 13;
(3)如图,在 AB是上方作等边△ABJ ,证明 JC BD,求出 JC的取值范围,可得结论.
【详解】解:(1)猜想 BD CE,理由如下:
BAE CAD,
BAE BAC CAD BAC,即 EAC BAD,
在 EAC和 BAD中,
AE AB
EAC BAD,
AC AD
EAC≌ BAD SAS ,
BD CE;
(2)在 AC的上方作等腰直角△ACE,使得 CAE 90 , AC AE,连接 BE.
ACB 45 , ACE 45
BCE 90
△BCE是直角三角形,
AC 2,
CE 2AC 2,
答案第 13页,共 14页
在Rt BCE中, BE BC2 CE2 42 22 2 5,
BAD CAE 90 ,
BAE DAC,
AB AD, AE AC,
ABE≌ ADC SAS ,
BE CD,
CD 2 5 ;
(3)如图,在 AB是上方作等边△ABJ ,
AD CD, ADC 60 ,
ADC是等边三角形,
BAJ CAD 60 ,
JAC BAD,
AJ AB, AC AD,
JAC≌ BAD SAS ,
CJ BD,
AB BJ 6,BC 13,
13 6 JC 13 6,
7 JC 19,
7 BD 19,
BD的最大值为19.
【点睛】本题是三角形综合题,考查了等腰直角三角形的性质和判定,全等三角形的判定和
性质,勾股定理,三角形三边的关系,等边三角形的性质等知识,添加恰当辅助线构造全等
三角形是本题的关键.
答案第 14页,共 14页
上学期 10 月月考数学试卷
一、单选题
1.中国“二十四节气”已被列入联合国教科文组织人类非物质文化遗产代表作名录,下
列四幅作品分别代 表“大雪”、“白露”、“芒种”、“立春”,其中是轴对称图形的是( )
A. B. C. D.
2.如图,若△ABC≌△DEF,且 AB 5,AC 6,BC 7,则 EF 的长为( )
A.5 B.6 C.7 D.8
3.如图,要测量池塘两岸相对的两点 A,B的距离,小明在池塘外取 AB的垂线 BF上
的点 C,D,使 BC CD,再画出 BF的垂线DE,使 E与 A,C在一条直线上,这时测
得DE的长就是 AB的长,依据是( )
A.SSS B.SAS C.ASA D.HL
4.在联欢会上,有 A、B、C三名选手站在一个三角形的三个顶点位置上,他们在玩“抢
凳子”游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳
子应放的最适当的位置是在 ABC的( )
A.三边垂直平分线的交点 B.三条中线的交点
C.三条角平分线的交点 D.三条高所在直线的交点
5.如图,在 ABC中, BAC=110 ,EF 是边 AB的垂直平分线,垂足为 E,交 BC于
F.MN是边 AC的垂直平分线,垂足为 M,交 BC于 N.连接 AF、 AN则 FAN 的度
数是( )
试卷第 1页,共 7页
A.70 B.55 C.40 D.30
6.如图,在 ABC中, C 90 , B 30 ,以 A为圆心,任意长为半径两弧分别交
1
AB、AC于点 M和 N,再分别以 M、N为圆心,大于 MN的长为半径画弧,两弧交于
2
点 P,连接 AP并延长交 BC于点 D,则下列说法中正确的个数是( )
① AD是 BAC的平分线;② ADC 60 ;③点 D在 AB的垂直平分线上;
④ S△DAC : S△ABD 1: 3.
A.4 B.3 C.2 D.1
7.如图,四边形 ABCD中, AB AD,点 B关于 AC的对称点 B 恰好落在CD上,若
BAD ,则 ACB的度数为( )
1
A. 45 B. 45 C. D.90
1
2 2
8.如果正整数 a、b、 c满足符式 a2 b2 c2,那么正整数、b、c叫做勾股数,某同
学将自己探究勾股数的过程列成下表,观察表中每列数的规律,可知 x y的值为( )
a b c
3 4 5
8 6 10
15 8 17
试卷第 2页,共 7页
24 10 26
x y 65
A. 47 B.62 C.79 D.98
二、填空题
9.在平面镜里看到背后墙上,电子钟示数如图所示,这时的时间应是 .
10.直角三角形两边长为 6和 8,则斜边中线长为 .
11.如图,在Rt△ABC中, C 90 ,AD平分 BAC,交 BC于点 D.DE AB于 E.若
BC 5, BD 3,则DE的长为 .
12.如图,在 ABC中, AD平分 BAC, AD BD于点 D,且 S ABC 10,则 ADC的
面积为 .
13.如图, ABC是等边三角形.D,E分别是 AC,BC上的点,若
AE AD, CED 20 .则 BAE .
试卷第 3页,共 7页
14.如图Rt△ABC中, C 90 ,分别以三角形各边为直径作半圆,图中阴影部分在
数学史上称为“希波克拉底月牙”;当 AC 3,BC 4时,阴影部分的面积为 .
15.在△ABC中,∠A=80°,当∠B= 时,△ABC是等腰三角形.
16.如图,∠AOB=45°,点M、N分别在射线 OA、OB上,MN=7,△OMN的面积为
14,P是直线MN上的动点,点 P关于 OA对称的点为 P1,点 P关于 OB对称点为 P2,
当点 P在直线 NM上运动时,△OP1P2的面积最小值为
三、解答题
17.如图,点 A、C、F、D在同一直线上, AF DC , A D ,AB DE .求证:
△ABC≌△DEF.
试卷第 4页,共 7页
18.如图,在边长为 1个单位长度的小正方形组成的网格中,点 A、B、C在小正方形
的顶点上.
(1)在图中画出与 ABC关于直线 l成轴对称的△A B C;
(2)在 l上找一点 P,使 PA PB的值最小;
(3)五边形 ABCB A 的面积为______.
19.如图,DE⊥AB于 E,DF AC于 F,若 BD=CD、 BE=CF,
(1)求证: BAD CAD;
(2)已知 AC 24, BE 6,求 AB的长.
20.中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和
地位,体现了数学研究中的继承和发展,现用 4个全等的直角三角形拼成如图所示“弦
图”.Rt△ABC中,∠ACB=90°.AC=b,BC=a,AB=c,请你利用这个图形解决下列
问题:
(1)试说明:a2+b2=c2;
(2)如果大正方形的面积是 13,小正方形的面积是 3,求(a+b)2的值.
试卷第 5页,共 7页
21.如图, AD,BE是 ABC的高线. AD与 BE相交于点 F,若 AD BD 6,且 ACD
的面积为 12,求线段 AF的长度.
22.如图所示,长方形纸片 ABCD的长 AD=8cm,宽 AB=4cm,将其沿着折痕 EF折
叠,使点 D与点 B重合.
(1)求证:BE=BF;
(2)求折叠后△BEF的面积.
23.已知线段 a和b.
(1)用直尺和圆规作等腰 ABC,使得 AB AC,BC a,BC边上的高 AD = b(保留作
图痕迹,不写作法);
(2)用直尺和圆规作等腰 ABC,使得 AB AC b, BC边上的高 AD a(保留作图痕
迹,不写作法).
24.【问题提出】
(1)如图 1,锐角 ABC中分别以 AB、AC为边向外作等腰 ABE和等腰 ACD,使
AE AB,AD AC, BAE CAD,连接 BD、CE,试猜想 BD与CE的数量关系,
试卷第 6页,共 7页
并说明理由;
AI
【探索研究】
(2)如图 2,在 ABC中, ACB 45 ,以 AB为直角边,点 A为直角顶点向外作等
腰直角△ABD,连接CD,若 AC 2,BC 4,求CD的长;
【解决问题】
(3)如图 3,在四边形 ABCD中, ADC 60 ,BC 13,AB 6,AD CD,则 BD的
最大值为_____.
试卷第 7页,共 7页
参考答案:
1.A
【分析】本题考查了轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对
称轴折叠后可重合.根据轴对称图形的知识求解.
【详解】解:A、是轴对称图形,故本选项符合题意;
B、不是轴对称图形,故本选项不符合题意;
C、不是轴对称图形,故本选项不符合题意;
D、不是轴对称图形,故本选项不符合题意.
故选:A.
2.C
【分析】本题主要考查了全等三角形的性质,根据全等三角形对应边相等即可得到
EF BC 7.
【详解】解:∵△ABC≌△DEF,BC 7,
∴EF BC 7,
故选 C.
3.C
【分析】本题主要考查了全等三角形的性质与判定,熟知全等三角形的判定定理是解题的关
键,全等三角形的判定定理有SSS,SAS,AAS,ASA,HL.
【详解】解:∵ AB⊥BF,DE⊥BF ,
∴ ABC EDC 90 ,
在 ABC和△EDC中,
ABC EDC
BC DC ,
ACB ECD
∴△ABC≌△EDC ASA ,
∴ AB DE ,
∴依据是ASA,
故选 C.
4.A
【分析】本题考查了线段垂直平分线的性质,熟练掌握线段垂直平分线上的到线段两端的距
答案第 1页,共 14页
离相等是解答本题的关键.根据线段垂直平分线的性质解答即可.
【详解】解:根据题意得:当木凳所在位置到 A、B、C三个顶点的距离相等时,游戏公平,
∵线段垂直平分线上的到线段两端的距离相等,
∴凳子应放的最适当的位置是在 ABC的三边垂直平分线的交点.
故选:A.
5.C
【分析】根据垂直平分线的性质得 AF BF, AN CN ,再由等边对等角,以及三角形内
角和定理求出所求角度数即可.
【详解】解:∵ EF 是边 AB的垂直平分线,MN是边 AC的垂直平分线,
∴ AF BF, AN CN ,
∴ BAF B, CAN C,
∵ BAC=110 ,
∴ B C 70 ,
∴ BAF CAN 70 ,
∴ FAN BAC BAF CAN 110 70 40 .
故选:C.
【点睛】此题考查了线段垂直平分线的性质,等腰三角形的性质,熟练掌握性质是解本题的
关键.线段垂直平分线上任意一点,到线段两端点的距离相等.
6.B
【分析】利用基本作图方法可对①进行判断;利用角平分线的定义计算出
BAD CAD 30 ,则由三角形内角和定理求出 ADC的度数,于是可对②进行判断;由
∠BAD ∠B得到DA DB,则根据线段垂直平分线的性质定理的逆定理可对③进行判断;
利用含30度的直角三角形三边的关系得到 AD 2CD,则 BD 2CD,然后根据三角形面积
公式可对④进行判断.
【详解】解:由作图方法可知 AD平分 BAC, 故①正确;
∵ C 90 , CAB 60 ,
∴ B 90 60 30 , BAD CAD 30 ,
∴ ADC 90 30 60 ,故②正确;
∵ B BAD 30 ,
∴ AD BD
答案第 2页,共 14页
∴点D在 AB的垂直平分线上,故③正确;
∵ CAD 30
∵ AD 2CD, C 90
∴BD AD 2CD,
∴BC 3CD,
S△DAC :S△ABD 1: 2,故④错误.
∴正确的有 3个,
故选 B.
【点睛】本题主要考查了角平分线的定义,角平分线的尺规作图,三角形内角和定理,等角
对等边,线段垂直平分线的判定,含 30度角的直角三角形的性质,熟练掌握各部分知识并
综合应用是解题的关键.
7.D
【分析】连接 AB , BB ,过 A作 AE⊥CD于 E,依据∠BAC= B AC,∠DAE= B AE,
1
即可得出∠CAE= ∠BAD,再根据四边形内角和以及三角形外角性质,即可得到∠ACB=
2
ACB 1=90° ∠BAD.
2
【详解】解:如图,连接 AB ,BB ,过 A作 AE⊥CD于 E,
∵点 B关于 AC的对称点 B 恰好落在 CD上,
∴AC垂直平分BB ,
∴AB= AB ,
∴∠BAC=∠ B AC,
∵AB=AD,
∴AD= AB ,
又∵AE⊥CD,
∴∠DAE=∠ B AE,
答案第 3页,共 14页
1 1
∴∠CAE= ∠BAD= α,
2 2
又∵ AEB = AOB =90°,
1
∴四边形 AOB E中, EB O=180° α,
2
1 1
∴ ACB = EB O COB =180° α 90°=90° α,
2 2
1
∴∠ACB= ACB =90° α,
2
故选:D.
【点睛】本题主要考查了轴对称的性质,四边形内角和以及三角形外角性质的运用,解决问
题的关键是作辅助线构造四边形 AOB E,解题时注意:如果两个图形关于某直线对称,那么
对称轴是任何一对对应点所连线段的垂直平分线.
8.C
【分析】依据每列数的规律,即可得到 a 2n,b n2 1,c n2 1,进而得出 x y的值.
【详解】解:由题可得,3 22 1,4 2 2,5 22 1,
a 2n,b n2 1,c n2 1,( n 2且 n为正整数)
当 c n2 1 65时,
解得: n 8,
x 16, y 63,
x y 79,
故选:C.
【点睛】本题主要考查了勾股数,满足 a2 b2 c2的三个正整数,称为勾股数.
9.10 : 51
【分析】在平面镜中的像与现实中的事物恰好顺序颠倒,且关于镜面对称,由此可解.
【详解】解:题中所给的“12 : 01”与“10 : 51”成轴对称,这时的时间应是10 : 51.
故答案为:10 : 51.
【点睛】本题考查镜面反射的原理与性质,解题的关键是掌握轴对称的性质.
10.5或 4/4或 5
【分析】根据两种情况:6和 8都为直角边;8为斜边,6为直角边,得到斜边长度,再利
用直角三角形斜边上的中线等于斜边的一半,即可解答.
【详解】解:当 6和 8都为直角三角形的直角边时,
答案第 4页,共 14页
根据勾股定理可得,直角三角形的斜边为 62 82 10,
斜边上的中线长为10 2 5;
当 8为直角三角形的斜边,6为直角三角形的直角边时,
斜边上的中线长为8 2 4,
综上所述,斜边中线长为 5或 4,
故答案为:5或 4.
【点睛】本题考查了勾股定理,直角三角形斜边上的中线等于斜边的一半,根据情况能够正
确地分类讨论是解题地关键.
11.2
【分析】本题考查了角平分线的性质,根据角平分线的性质得出DE CD即可求解.
【详解】解:∵ AD平分 BAC, AC CD,DE AB,
∴CD DE,
∵BC 5,BD 3,
∴CD DE 5 3 2,
故答案为:2.
12.5
【分析】延长 BD交 AC于 E,证明 ABD≌ AED ASA ,利用三角形的中线平分三角形的
面积和全等三角形的面积相等,即可得解.
【详解】解:如图,延长BD交 AC于 E,
∵ AD平分 BAC,
∴ BAD CAD,
在△ABD和△AED中,
BAD CAD
AD AD
ADB ADE
答案第 5页,共 14页
∴ ABD≌ AED ASA ,
∴BD DE,
∴ S ABD S AED, S BDC S CDE ,
∴ S ADC S
1
CDE S ADE S2 ABC
5,
故答案为:5.
【点睛】本题考查全等三角形的判定和性质,以及三角形的中线平分三角形的面积.遇到角
平分线和垂线,常常构造等腰三角形来进行解题.通过构造等腰三角形证明三角形全等是解
题的关键.
13. 40
【分析】利用等边三角形的性质可得 C BAC 60 ,从而利用三角形的外角性质可得
ADE 80 ,然后利用等腰三角形的性质可得 AED ADE 80 ,从而利用三角形的内
角和定理可得 DAE 20 ,最后利用角的和差关系进行计算即可解答.
【详解】解:∵ ABC是等边三角形,
∴ C BAC 60 ,
∵ CED 20 ,
∴ ADE CED C 80 ,
∵ AE AD,
∴ AED ADE 80 ,
∴ DAE 180 AED ADE 20 ,
∴ BAE BAC DAE 60 20 40 ,
故答案为:40.
【点睛】本题考查了等边三角形的性质,三角形外角的性质,等腰三角形的性质,三角形内
角和定理,熟练掌握等边三角形的性质是解题的关键.
14.6
【分析】本题主要考查了求不规则图形的面积,勾股定理,根据勾股定理求得 AB的长度,
再根据圆的面积公式分别计算三个半圆的面积,最后根据阴影部分的面积等于两个较小半圆
的面积和减去以 AB为直径的半圆的面积,之后再加上 ABC的面积进行求解即可.
【详解】解:∵在Rt△ABC中, ACB 90 , AC 3, BC 4,
答案第 6页,共 14页
∴AB AC2 BC2 32 42 5,
3 2
以 AC为直径得到半圆的面积: 2 9 ;
2 8
4 2
以BC 为直径半圆的面积: 2 ; 2
2
5
2
以 AB 为直径半圆的面积: 2 25 ;
2 8
1 1
Rt△ABC的面积为: AC BC 3 4 6,
2 2
∴阴影部分的面积 S半圆AC S半圆BC S半圆AB S△ABC
9 2 25 6 6 .
8 8
故答案为:6.
15.20°或 50°或 80°
【分析】分三种情况分析, A是顶角, B是顶角, C是顶角,
【详解】∵ A 80 ,
∴①当 C是顶角, B A 80 时,△ABC是等腰三角形;
②当 A是顶角,∠B=(180°﹣80°)÷2=50°时,△ABC是等腰三角形;
③ B是顶角,∠B=180°﹣80°×2=20°时,△ABC是等腰三角形;
故答案为:80°或 50°或 20°
16.8
【分析】连接 OP,过点 O作 OH NM交 NM的延长线于 H,首先利用三角形的面积公式
求出 OH,再证明△OP1P2是等腰直角三角形,当 OP最小时,△OP1P2的面积最小.
【详解】解:如图所示,连接 OP,过点 O作 OH NM交 NM的延长线于 H,
答案第 7页,共 14页
∵S
1
△OMN= MN OH=14,且MN=7,,∴OH=4,2
∵点 P关于 OA对称的点为 P1,点 P关于 OB对称点为 P2,
∴ AOP= AOP1, BOP= BOP2,OP=OP1=OP2,
∵∠AOB=45°,
∴ P1OP2=2( POA+ POB)=90 ,
∴△OP1P2是等腰直角三角形,
∴当OP=OP1最小时,△OP1P2的面积最小,
根据垂线段最短可知,OP的最小值为 4,
1
∴△OP1P2的面积的最小值= 4 4=8,2
故答案为:8.
【点睛】本题主要考查了角平分线的应用及垂线段最短的公理,解题的关键在于证明△OP1P2
是等腰直角三角形,找到 OP的最小值.
17.见解析
【分析】由 AF CD,可求得 AC DF,利用SAS可得出结论.
【详解】解: AF CD,
∴AF FC CD FC,即 AC DF,
AB DE
在 ABC和 DEF中, A D ,
AC DF
∴△ABC≌△DEF (SAS) .
【点睛】本题主要考查全等三角形的判定,掌握全等三角形的判定方法是解题的关键.
18.(1)见解析
(2)见解析
(3)13
【分析】本题考查了轴对称-最短路线问题,作图-轴对称变换.
(1)根据题意作出点 A,点 B关于 l的对称点 A 、 B ,连结CA , A B , B C即可;
(2)通过轴对称的性质,作出图形即可;
答案第 8页,共 14页
(3)割补法利用矩形面积减去 4个直角三角形面积求解即可得到结论.
【详解】(1)作出点 A,点 B关于 l的对称点 A 、 B ,连结CA , A B ,B C,
如图所示,△A B C即为所求;
(2)∵点 B与点 B 关于 l对称,
连接 AB 交直线 l与点 P,
∴PB PB ,
∴PA PB PA PB ,
则PA PB长的最短值 AB .
1 1 1 1
(3)五边形 ABCB A 的面积 6 4 1 2 1 2 3 3 3 3 13 ,
2 2 2 2
故答案为:13
19.(1)见解析
(2)12
【分析】(1)由题所给条件可得△BED≌△CFD,即得DE=DF,则 EAD CAD.
(2)由(1)问所得条件证得△ADE≌△ADF,得 AE AF 24 6 18,则
AB AE BE 18 6 12.
【详解】(1)证明:∵DE⊥AB, DF AC,
∴ E= DFC=90 ,
在Rt△BED和 RtVCFD中,
答案第 9页,共 14页
BD=CD
BE=CF
,
∴Rt BED≌Rt CFD HL ,
∴DE=DF,
∵DE⊥AB,DF AC,
∴AD平分 BAC,
∴ BAD CAD;
(2)解:∵ BAD CAD, E AFD,DE=DF,
∴△ADE≌△ADF AAS ,
∴ AE=AF,CF BE 6,
∵ AC 24,
∴ AE AF 24 6 18,
∴ AB AE BE 18 6 12.
【点睛】本题考查了全等三角形的性质和判定的应用,注意:全等三角形的判定定理有 SAS,
ASA,AAS,SSS,全等三角形的对应边相等,对应角相等.
20.(1)证明见解析;(2)23
【分析】(1)根据题意,我们可在图中找等量关系,由中间的小正方形的面积等于大正方形
的面积减去四个直角三角形的面积,列出等式化简即可得出勾股定理的表达式.
(2)根据完全平方公式的变形解答即可.
【详解】解:(1 1)∵大正方形面积为 c2,直角三角形面积为 2 ab,小正方形面积为(b﹣a)
2,
∴c2=4× 12 ab+(a﹣b)
2=2ab+a2﹣2ab+b2即 c2=a2+b2;
(2)由图可知:
(b a 1﹣ )2=3,4× 2 ab=13﹣3=10,
∴2ab=10,
∴(a+b)2=(b﹣a)2+4ab=3+2×10=23.
【点睛】本题考查了对勾股定理的证明和以及非负数的性质,掌握三角形和正方形面积计算
公式是解决问题的关键.
答案第 10页,共 14页
21.2
【分析】本题主要考查了全等三角形的判定与性质,三角形的面积等知识,利用ASA证明
△ACD≌△BFD ,得DF DC,再根据三角形面积可得CD的长,从而可得答案.
【详解】解:∵ AD, BE是 ABC的高线,
∴ ADB ADC AEB 90 ,
∵ BFD AFE,
∴ DBF CAD,
在 ACD和△BFD中,
CAD DBF
BD AD ,
BDF ADC
∴ ACD≌ BFD ASA ,
∴DF DC,
∵ ACD的面积为 12,
1
∴ CD 6 12,
2
∴CD 4,
∴DF 4,
∴ AF AD DF 2.
22.(1)证明见解析;(2)10
【分析】(1)根据轴对称的性质,得∠BEF=∠DEF;根据长方形和平行线性质,得∠BFE
=∠DEF,从而得∠BFE=∠BEF,结合等腰三角形性质,即可完成证明;
(2)结合题意设 AE=x,则 BE=DE=8﹣x;根据勾股定理的性质,通过列方程并求解,
即可得到 AE;再结合三角形的性质计算,即可得到答案.
【详解】(1)由折叠的性质得:∠BEF=∠DEF,
∵AD // BC,
∴∠BFE=∠DEF,
∴∠BFE=∠BEF,
∴BE=BF;
(2)设 AE=x,则 BE=DE=8﹣x,
答案第 11页,共 14页
在 Rt△ABE中,由勾股定理得:x2+42=(8﹣x)2
解得,x=3,
∴BE=BF=5,
∴△BEF 1 1的面积= 2 ×BF×AB= 2 ×5×4=10.
【点睛】本题考查了轴对称、矩形、平行线、等腰三角形、一元一次方程、勾股定理的知识;
解题的关键是熟练掌握矩形、轴对称、勾股定理的性质,从而完成求解.
23.(1)作图见详解
(2)作图见详解
【分析】(1)先作 BC a,再作BC的垂直平分线交 BC于D点,接着在BC的垂直平分线
上截取DA b,然后连接 AB、 AC得到 ABC;
(2)先过直线 l上的点D作直线 l的垂线,再在垂线上截取DA a,然后以点A为圆心,b
为半径画弧,分别交直线 l于点 B、C,连接 AB、 AC, ABC满足条件.
【详解】(1)解:如图 1,
ABC为所要求图形.
(2)解:如图 2,
ABC为所要求图形.
答案第 12页,共 14页
【点睛】本题考查了作图—复杂作图,等腰三角形的判断与性质.解决此类题目的关键是熟
悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.
24.(1)猜想 BD CE,理由见解析;(2) 2 5;(3)19
【分析】(1)首先根据等式的性质证明 EAC BAD,则根据SAS即可证明
△EAC≌△BAD,根据全等三角形的性质即可证明.
(2)在 AC的上方作等腰直角△ACE,使得 CAE 90 , AC AE,连接 BE,由勾股定
理可求 BE的长,由“SAS ”可证△ABE≌△ADC ,得出CD BE 13;
(3)如图,在 AB是上方作等边△ABJ ,证明 JC BD,求出 JC的取值范围,可得结论.
【详解】解:(1)猜想 BD CE,理由如下:
BAE CAD,
BAE BAC CAD BAC,即 EAC BAD,
在 EAC和 BAD中,
AE AB
EAC BAD,
AC AD
EAC≌ BAD SAS ,
BD CE;
(2)在 AC的上方作等腰直角△ACE,使得 CAE 90 , AC AE,连接 BE.
ACB 45 , ACE 45
BCE 90
△BCE是直角三角形,
AC 2,
CE 2AC 2,
答案第 13页,共 14页
在Rt BCE中, BE BC2 CE2 42 22 2 5,
BAD CAE 90 ,
BAE DAC,
AB AD, AE AC,
ABE≌ ADC SAS ,
BE CD,
CD 2 5 ;
(3)如图,在 AB是上方作等边△ABJ ,
AD CD, ADC 60 ,
ADC是等边三角形,
BAJ CAD 60 ,
JAC BAD,
AJ AB, AC AD,
JAC≌ BAD SAS ,
CJ BD,
AB BJ 6,BC 13,
13 6 JC 13 6,
7 JC 19,
7 BD 19,
BD的最大值为19.
【点睛】本题是三角形综合题,考查了等腰直角三角形的性质和判定,全等三角形的判定和
性质,勾股定理,三角形三边的关系,等边三角形的性质等知识,添加恰当辅助线构造全等
三角形是本题的关键.
答案第 14页,共 14页
同课章节目录
