人教版九年级数学下册综合测试卷(含答案)
文档属性
| 名称 | 人教版九年级数学下册综合测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-09 22:42:08 | ||
图片预览




文档简介
人教版九年级数学下册综合测试卷
(时间:120 分钟 满分:120 分)
题号 第 Ⅰ卷 第Ⅱ卷 总分
1-16 17 18 19 20 21 22 23 24 25 26
得分
第 Ⅰ卷(选择题 共 42 分)
一、选择题(本大题共 16 小题,1~10小题,每小题3分,11~16 小题,每小题2分,共42分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1. 2sin60°的值等于 ( )
A.1 B. C. D.2
2.下列几何体中,主视图是三角形的是 ( )
3.若点 A(3,-4),B(-2,m)在同一个反比例函数的图象上,则m的值为 ( )
A.6 B. -6 C.12 D. -12
4.某厂现有 300t煤,这些煤能烧的天数y与平均每天烧的吨数x之间的函数关系是 ( )
C. y=300x(x≥0) D. y=300x(x>0)
5.如图,在5×4的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,则 sin∠BAC的值为 ( )
A. B. C. D.
中小学教育资源及组卷应用平台
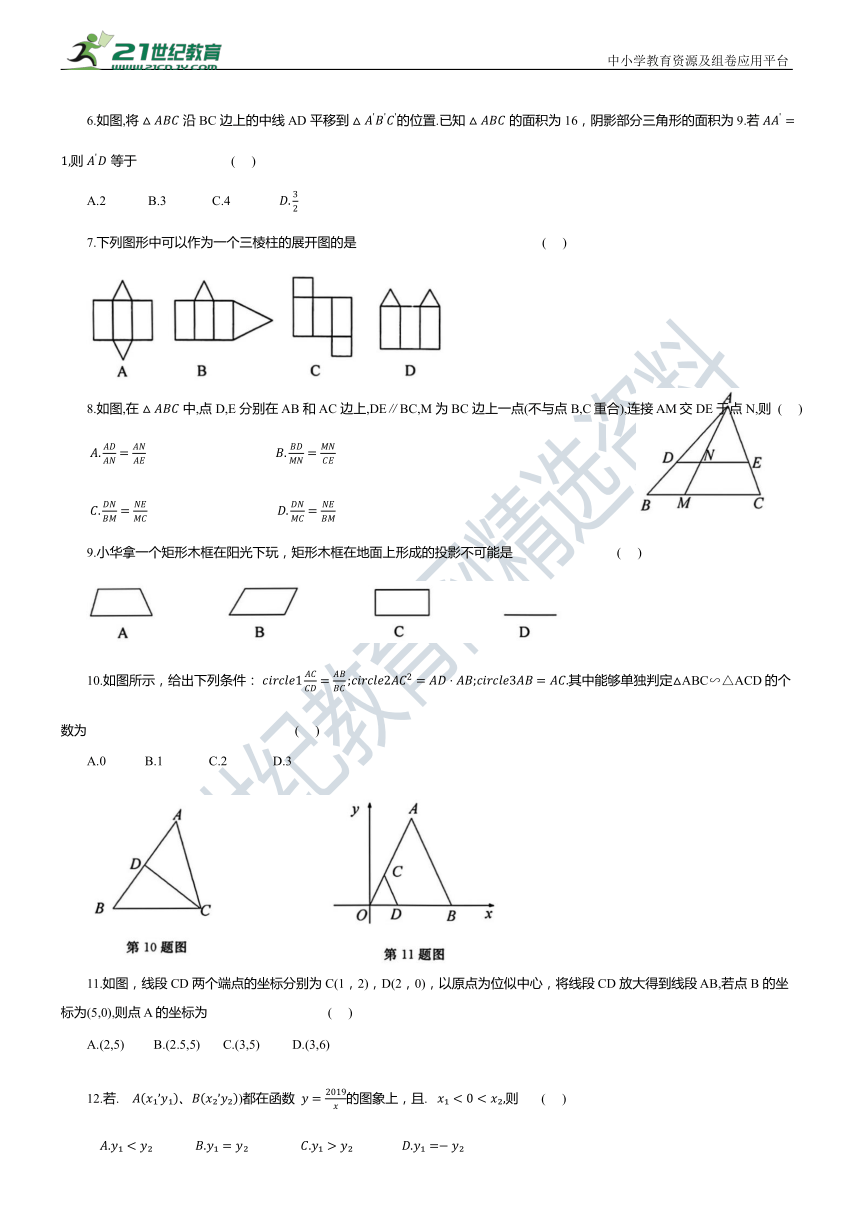
6.如图,将 沿 BC 边上的中线AD 平移到 的位置.已知 的面积为 16,阴影部分三角形的面积为9.若 则 等于 ( )
A.2 B.3 C.4
7.下列图形中可以作为一个三棱柱的展开图的是 ( )
8.如图,在 中,点 D,E 分别在AB 和AC 边上,DE∥BC,M 为BC 边上一点(不与点 B,C重合),连接 AM交 DE 于点 N,则 ( )
9.小华拿一个矩形木框在阳光下玩,矩形木框在地面上形成的投影不可能是 ( )
10.如图所示,给出下列条件: 其中能够单独判定△ABC∽△ACD的个数为 ( )
A.0 B.1 C.2 D.3
11.如图,线段CD 两个端点的坐标分别为C(1,2),D(2,0),以原点为位似中心,将线段 CD 放大得到线段 AB,若点 B 的坐标为(5,0),则点 A 的坐标为 ( )
A.(2,5) B.(2.5,5) C.(3,5) D.(3,6)
12.若. )都在函数 的图象上,且. 则 ( )
13.如图是一个几何体的三视图,该几何体的表面积为 ( )
A.50π B.100π
C.150π D.175π
14.若反比例函数 的图象上有两个不同的点关于y轴的对称点都在一次函数y=-x+m的图象上,则 m的取值范围是
或
15.如图,在 Rt△ABC中, 以 AB的中点O为圆心,OA 的长为半径作半圆交AC 于点 D,则图中阴影部分的面积为 ( )
16.已知一次函数 y=ax+b与反比例函数. 其中 ab<0,a,b.为常数,它们在同一坐标系中的图象可以是 ( )
第Ⅱ卷(非选择题 共 78 分)
二、填空题(本大题共3 小题,共 11分;17 小题3 分;18、19 小题,每小题4分.请把答案填在题中的横线上)
17.如图,点 A 是反比例函数 图象上一点,过点 A 作x轴的平行线,交反比例函数 y 的图象于点 B,连接OA,OB,若 则
18.直角三角形纸片的两直角边长分别是6,8,现将 按如图那样折叠,使点 A 与点 B 重合,折痕为 DE,则 的值是 ,cos∠CBE的值是 .
19.勘测队按实际需要构建了平面直角坐标系,并标示了A,B,C三地的坐标,数据如图(单位:km).笔直铁路经过A,B两地.
(1)A,B间的距离为 km;
(2)计划修一条从C到铁路AB 的最短公路l,并在l上建一个维修站D,使 D到A,C的距离相等,则C,D间的距离为 km.
三、解答题(本大题共7小题,共 67分.解答应写出必要的文字说明、证明过程或演算步骤)
20.(本小题满分8分)计算
(1)
21.(本小题满分 8分)
如图,图中的小方格都是边长为1的正方形, 与 是以点O 为 位似中心的图形,它们的顶点都在小正方形的顶点上.
(1)画出位似中心 O;
(2)求 与 的位似比;
(3)以点O 为位似中心,再画一个 使它与 的位似比等于 1.5.
22.(本小题满分8分)
如图是由一些棱长都为 1 cm的小正方体组合成的简单几何体.
(1)该几何体的表面积(含下底面)为 ;
(2)该几何体的主视图如图所示,请在图中所示的方格纸中分别画出它的左视图和俯视图.
23.(本小题满分8分)
某同学想测旗杆的高度,他在某一时刻测得长为 1m 的竹竿 EF竖直时的影长FM 为 1.5m ,同一时刻测量旗杆 AB的影长时,因旗杆AB靠近一幢楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地上的影长BC为9m,留在墙上的影长CD为2m,求旗杆 AB 的高度.
24.(本小题满分 10 分)
如图,一次函数 为常数, )的图象与反比例函数 的图象交于点 A(m,8)与点 B(4,2).
(1)求一次函数与反比例函数的解析式;
(2)根据图象说明,当x为何值时,
25.(本小题满分 12 分)
如图所示是我国古代城市用以滞洪或分洪系统的局部截面原理图,图中 OP 为下水管道口直径,OB 为可绕转轴O自由转动的阀门.平时阀门被管道中排出的水冲开,可排出城市污水;当河水上涨时,阀门会因河水压迫而关闭,以防河水倒灌入城中.若阀门的直径( OA 为检修时阀门开启的位置,且(
(1)直接写出阀门被下水道的水冲开与被河水关闭过程中 的取值范围;
(2)为了观测水位,当下水道的水冲开阀门到达OB 位置时,在点 A 处测得俯角 若此时点 B恰好与下水道的水平面齐平,求此时下水道内水的深度.(结果保留小数点后一位)
( ︿ 0.92,
26.(本小题满分 13 分)
如图 1,在正方形 ABCD中, M 是对角线 BD 上的一个动点( 连接 AM,过点 M 作. 交边 BC 于点 N.
(1)如图 1,求证:
(2)如图2,连接AN,O为AN 的中点,MO的延长线交边AB 于点P,当 时,求 AN 和PM的长;
一、1. C 2. C 3. A 4. B 5. D 6. B 7. A 8. C 9. A 10. B 11. B 12.A 13. C 14. C 15. A 16. C
二、17.5 19.(1)20 (2)13
三、20.(1)-3
21.解:(1)如图,点 O 即为所求;
(3)如图,△A B C 即为所求.
22.(1)26 cm (2)略
23.解:分别连接 AD,EM,过点 D 作 DN⊥AB,垂足为点 N. 由题意得△EFM∽△AND,四边形 BCDN 为矩形,
∴BN=CD=2m ,ND=BC=9 m.
即1/AN=1. ,∴AN=6,∴AB=AN+BN=6+2=8(m).
答:旗杆 AB 的高度为 8 m.
24.解:(1)把点 B(4,2)代入 得: ∴反比例函数解析式为 将点 A(m,8)代入 y 得: 解得 m=1,∴A(1,8),将A(1,8)、B(4,2)代入 得 解得 一次函数的解析式为:
(2)由图象可知:当04时, 即
25.解:(1)阀门OB 被下水道的水冲开与被河水关闭过程中, ≤90°.
(2)∵OA⊥AC,∠CAB=67.5°,∴∠BAO=22.5°,
∵OA=OB,∴∠BAO=∠ABO=22.5°,
∴∠BOD=45°,
过点 B 作 BD⊥OP于点 D,
在 Rt△BOD中,∵OB=OP=100,∴OD=50 ,
所以,此时下水道内水的深度约为 29.5(cm).
26.解:(1)证明:如图.过点 M 作 MF⊥AB 于 F,作 MG⊥BC于 G,
∴∠MFB=∠BGM=90°.
∵正方形 ABCD,
同理可证:∠DBC=45°,∴∠ABD=∠DBC.
∵MF⊥AB,MG⊥BC,∴MF=MG.
∵正方形 ABCD,∴∠ABN=90°,
∵MN⊥AM,∴∠NMA=90°,
(2)如图,在 中,
在 中,∵∠DBC=45°,∴∠MAN=∠DBC,
∵在 Rt△ABD中,
∴在 Rt△ABN中,
∵在 Rt△AMN 中,MA=MN,O是AN 的中点,
OM⊥AN,∴PM⊥AN,∴∠AOP=90°,∴∠AOP=∠ABN=90°,
又∵∠PAO=∠NAB,∴△AOP∽△ABN.∴OP=AC,
(时间:120 分钟 满分:120 分)
题号 第 Ⅰ卷 第Ⅱ卷 总分
1-16 17 18 19 20 21 22 23 24 25 26
得分
第 Ⅰ卷(选择题 共 42 分)
一、选择题(本大题共 16 小题,1~10小题,每小题3分,11~16 小题,每小题2分,共42分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1. 2sin60°的值等于 ( )
A.1 B. C. D.2
2.下列几何体中,主视图是三角形的是 ( )
3.若点 A(3,-4),B(-2,m)在同一个反比例函数的图象上,则m的值为 ( )
A.6 B. -6 C.12 D. -12
4.某厂现有 300t煤,这些煤能烧的天数y与平均每天烧的吨数x之间的函数关系是 ( )
C. y=300x(x≥0) D. y=300x(x>0)
5.如图,在5×4的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,则 sin∠BAC的值为 ( )
A. B. C. D.
中小学教育资源及组卷应用平台
6.如图,将 沿 BC 边上的中线AD 平移到 的位置.已知 的面积为 16,阴影部分三角形的面积为9.若 则 等于 ( )
A.2 B.3 C.4
7.下列图形中可以作为一个三棱柱的展开图的是 ( )
8.如图,在 中,点 D,E 分别在AB 和AC 边上,DE∥BC,M 为BC 边上一点(不与点 B,C重合),连接 AM交 DE 于点 N,则 ( )
9.小华拿一个矩形木框在阳光下玩,矩形木框在地面上形成的投影不可能是 ( )
10.如图所示,给出下列条件: 其中能够单独判定△ABC∽△ACD的个数为 ( )
A.0 B.1 C.2 D.3
11.如图,线段CD 两个端点的坐标分别为C(1,2),D(2,0),以原点为位似中心,将线段 CD 放大得到线段 AB,若点 B 的坐标为(5,0),则点 A 的坐标为 ( )
A.(2,5) B.(2.5,5) C.(3,5) D.(3,6)
12.若. )都在函数 的图象上,且. 则 ( )
13.如图是一个几何体的三视图,该几何体的表面积为 ( )
A.50π B.100π
C.150π D.175π
14.若反比例函数 的图象上有两个不同的点关于y轴的对称点都在一次函数y=-x+m的图象上,则 m的取值范围是
或
15.如图,在 Rt△ABC中, 以 AB的中点O为圆心,OA 的长为半径作半圆交AC 于点 D,则图中阴影部分的面积为 ( )
16.已知一次函数 y=ax+b与反比例函数. 其中 ab<0,a,b.为常数,它们在同一坐标系中的图象可以是 ( )
第Ⅱ卷(非选择题 共 78 分)
二、填空题(本大题共3 小题,共 11分;17 小题3 分;18、19 小题,每小题4分.请把答案填在题中的横线上)
17.如图,点 A 是反比例函数 图象上一点,过点 A 作x轴的平行线,交反比例函数 y 的图象于点 B,连接OA,OB,若 则
18.直角三角形纸片的两直角边长分别是6,8,现将 按如图那样折叠,使点 A 与点 B 重合,折痕为 DE,则 的值是 ,cos∠CBE的值是 .
19.勘测队按实际需要构建了平面直角坐标系,并标示了A,B,C三地的坐标,数据如图(单位:km).笔直铁路经过A,B两地.
(1)A,B间的距离为 km;
(2)计划修一条从C到铁路AB 的最短公路l,并在l上建一个维修站D,使 D到A,C的距离相等,则C,D间的距离为 km.
三、解答题(本大题共7小题,共 67分.解答应写出必要的文字说明、证明过程或演算步骤)
20.(本小题满分8分)计算
(1)
21.(本小题满分 8分)
如图,图中的小方格都是边长为1的正方形, 与 是以点O 为 位似中心的图形,它们的顶点都在小正方形的顶点上.
(1)画出位似中心 O;
(2)求 与 的位似比;
(3)以点O 为位似中心,再画一个 使它与 的位似比等于 1.5.
22.(本小题满分8分)
如图是由一些棱长都为 1 cm的小正方体组合成的简单几何体.
(1)该几何体的表面积(含下底面)为 ;
(2)该几何体的主视图如图所示,请在图中所示的方格纸中分别画出它的左视图和俯视图.
23.(本小题满分8分)
某同学想测旗杆的高度,他在某一时刻测得长为 1m 的竹竿 EF竖直时的影长FM 为 1.5m ,同一时刻测量旗杆 AB的影长时,因旗杆AB靠近一幢楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地上的影长BC为9m,留在墙上的影长CD为2m,求旗杆 AB 的高度.
24.(本小题满分 10 分)
如图,一次函数 为常数, )的图象与反比例函数 的图象交于点 A(m,8)与点 B(4,2).
(1)求一次函数与反比例函数的解析式;
(2)根据图象说明,当x为何值时,
25.(本小题满分 12 分)
如图所示是我国古代城市用以滞洪或分洪系统的局部截面原理图,图中 OP 为下水管道口直径,OB 为可绕转轴O自由转动的阀门.平时阀门被管道中排出的水冲开,可排出城市污水;当河水上涨时,阀门会因河水压迫而关闭,以防河水倒灌入城中.若阀门的直径( OA 为检修时阀门开启的位置,且(
(1)直接写出阀门被下水道的水冲开与被河水关闭过程中 的取值范围;
(2)为了观测水位,当下水道的水冲开阀门到达OB 位置时,在点 A 处测得俯角 若此时点 B恰好与下水道的水平面齐平,求此时下水道内水的深度.(结果保留小数点后一位)
( ︿ 0.92,
26.(本小题满分 13 分)
如图 1,在正方形 ABCD中, M 是对角线 BD 上的一个动点( 连接 AM,过点 M 作. 交边 BC 于点 N.
(1)如图 1,求证:
(2)如图2,连接AN,O为AN 的中点,MO的延长线交边AB 于点P,当 时,求 AN 和PM的长;
一、1. C 2. C 3. A 4. B 5. D 6. B 7. A 8. C 9. A 10. B 11. B 12.A 13. C 14. C 15. A 16. C
二、17.5 19.(1)20 (2)13
三、20.(1)-3
21.解:(1)如图,点 O 即为所求;
(3)如图,△A B C 即为所求.
22.(1)26 cm (2)略
23.解:分别连接 AD,EM,过点 D 作 DN⊥AB,垂足为点 N. 由题意得△EFM∽△AND,四边形 BCDN 为矩形,
∴BN=CD=2m ,ND=BC=9 m.
即1/AN=1. ,∴AN=6,∴AB=AN+BN=6+2=8(m).
答:旗杆 AB 的高度为 8 m.
24.解:(1)把点 B(4,2)代入 得: ∴反比例函数解析式为 将点 A(m,8)代入 y 得: 解得 m=1,∴A(1,8),将A(1,8)、B(4,2)代入 得 解得 一次函数的解析式为:
(2)由图象可知:当0
25.解:(1)阀门OB 被下水道的水冲开与被河水关闭过程中, ≤90°.
(2)∵OA⊥AC,∠CAB=67.5°,∴∠BAO=22.5°,
∵OA=OB,∴∠BAO=∠ABO=22.5°,
∴∠BOD=45°,
过点 B 作 BD⊥OP于点 D,
在 Rt△BOD中,∵OB=OP=100,∴OD=50 ,
所以,此时下水道内水的深度约为 29.5(cm).
26.解:(1)证明:如图.过点 M 作 MF⊥AB 于 F,作 MG⊥BC于 G,
∴∠MFB=∠BGM=90°.
∵正方形 ABCD,
同理可证:∠DBC=45°,∴∠ABD=∠DBC.
∵MF⊥AB,MG⊥BC,∴MF=MG.
∵正方形 ABCD,∴∠ABN=90°,
∵MN⊥AM,∴∠NMA=90°,
(2)如图,在 中,
在 中,∵∠DBC=45°,∴∠MAN=∠DBC,
∵在 Rt△ABD中,
∴在 Rt△ABN中,
∵在 Rt△AMN 中,MA=MN,O是AN 的中点,
OM⊥AN,∴PM⊥AN,∴∠AOP=90°,∴∠AOP=∠ABN=90°,
又∵∠PAO=∠NAB,∴△AOP∽△ABN.∴OP=AC,
