6.3 等可能事件的概率(第3课时) 课件(共36张PPT)
文档属性
| 名称 | 6.3 等可能事件的概率(第3课时) 课件(共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 00:00:00 | ||
图片预览











文档简介
(共36张PPT)
6.3 与面积相关的概率
1.了解面积相等的几何概率的计算方法,并能进行简单计算,能设计符合要求的简单概率模型。
2.在具体情境中进一步了解概率的意义,体会概率是描述不确定现象的数学模型。
【教学重点】
会进行简单的概率计算.
【教学难点】
会进行简单的概率计算.
1、摸到红球的概率?
P(摸到红球)=
摸出红球可能出现的结果数
摸出任一球所有可能的结果数
不确定事件发生的可能性
2.事件发生的可能性是有大小的。
必然事件发生的可能性是
1,
不可能事件发生的可能性是
0,
大于0而小于1。
请一位同学在以下8张背面完全相同的扑克牌中任意抽取一张,请问:
P(抽到红心3)= P(抽到黑色)=
P(抽到奇数)= P(抽到黑桃)=
在一些商场中我们可以看到抽奖的转盘,想一想抽中图中各奖励的概率是一样的吗?
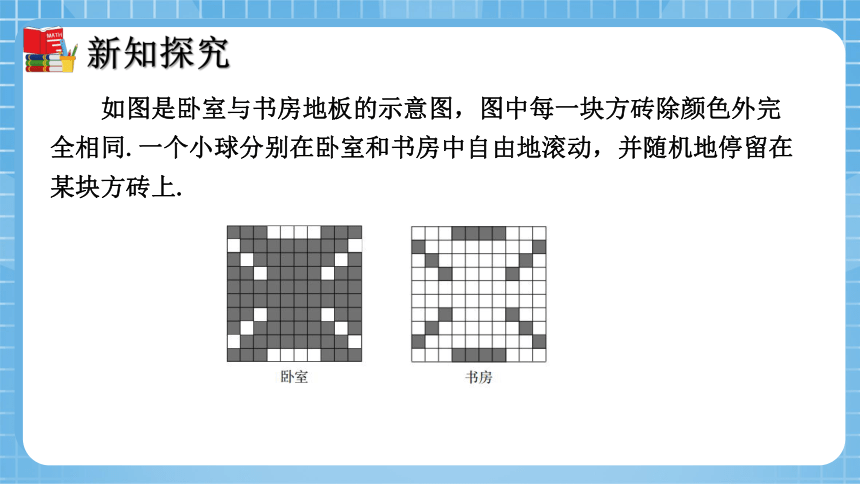
如图是卧室与书房地板的示意图,图中每一块方砖除颜色外完全相同.一个小球分别在卧室和书房中自由地滚动,并随机地停留在某块方砖上.
(1)在哪个房间,小球停留在黑砖上的概率大?为什么?
(2)你觉得小球停留在黑砖上的概率大小与什么有关?
(1)在卧室里小球停留在黑砖上的概率大,因为卧室和书房的方砖总块数相等,而卧室的黑砖块数大于书房的黑砖块数,所以在卧室里小球停留在黑砖上的概率大.
(2)与黑砖的块数与方砖总块数的比值的大小有关.
某事件发生的概率等于该事件发生的所有可能结果所组成的图形的面积 SA 与所有可能结果所组成的图形的总面积 S全 的比值.即
与几何图形有关的简单事件发生的概率
如果小球在如图所示的地板上自由地滚动,并随机停留在某块方砖上,它最终停留在黑砖上的概率是多少?
1.题中所说“自由地滚动,并随机停留在某块方砖上”说明了什么?
小球停留在任何一块方砖上的概率都相等.
2.小球停留在方砖上所有可能出现的结果有多少种?停留在黑砖上可能出现的结果有多少种?
小球停留在方砖上所有可能的结果有20种,停留在黑砖上可能出现的结果有5种.
P (小球最终停留在黑砖上)
P (小球最终停留在白砖上) ,
P (小球最终停留在黑砖上) + P (小球最终停留在白砖上) =1 .
3.小球停留在白砖上的概率是多少?它与停留在黑砖上的概率有何关系?
几何概型:
P(A)=
A事件可能出现的结果组成的图形面积(长度或体积)
所有可能出现的结果组成的图形面积(长度或体积)
以几何图形为背景的一种概率模型,在这个模型下,随机试验所有可能的结果发生的概率是相同的.
一般地,在一次试验中,结果落在区域D中每一点都是等可能的,用A表示“试验结果落在D中的一个小区域M中”这个事件,那么事件A发生的概率为
P(A)= .
M的面积(长度或体积)
D的面积(长度或体积)
A事件所占试验区域的份数m
试验区域总份数n
P(A)= .
部分问题可转化为:
D
M
例1.一位汽车司机准备去商场购物,然后他随意把汽车停在某个停车场内,停车场内一个停车位置正好占一个方格且一个方格除颜色外完全一样,则汽车停在红色区域的概率是____.
在上题中,
(1)小球最终停留在白砖上的概率是多少?
(2)小明认为(1)的概率与下面事件发生的概率相等:一个
袋中装有 20 个球,其中有 5 个黑球和 15 个白球,每个球除颜色外都相同,从中任意摸出一个球是白球.
你同意他的想法吗?
等于
P(小球最终停留在白砖上)
(2)同意。因为袋中共有20个球,这些球除颜色外其他都相同,从中任意摸出一个球,这20个球被摸到的概率都相等,所以P(任意摸出一球是白球)
例2.某商场为了吸引顾客,设立了一个可以自由转动的转盘,并规定:顾客每购买 100 元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红、黄或绿色区域, 顾客就可以分别获得 100 元、50 元、20 元的购物券(转盘被等分成 20 个扇形).
甲顾客购物 120 元,他获得购物券的概率是多少?他得到 100元、50元、20元购物券的概率分别是多少?
解:甲顾客的消费额在 100 元到 200 元之间,因此可以获得一次转动转盘的机会.
转盘被等分成 20 个扇形,其中 1 个是红色、2个是黄色、4个是绿色,因此,对于甲顾客来说,
P(获得购物券)
P(获得100元购物券)
P(获得50元购物券)
P(获得20元购物券)
指针不是落在红色区域就是落在白色区域, 落在红色区域和白色区域的概率相等, 所以P(落在红色区域)=
P(落在白色区域)=
如图是一个可以自由转动的转盘, 转动转盘, 当转盘停止时, 指针落在红色区域和白色区域的概率分别是多少?
先把白色区域等分成2份,这样转盘被等分成3个扇形区域,其中1个是红色,2个是白色,所以P(落在红色区域)= ,P(落在白色区域)=
你认为谁做得对?说说你的理由,你是怎样做的?
第2位同学做得对.理由:因为整个圆的圆心角为360°,红色区域扇形的圆心角为120°,则白色区域扇形的圆心角为240°,因此P(落在红色区域)= ,P(落在白色区域)=
例3.某路口南北方向红绿灯的设置时间为:红灯20秒、绿灯60秒、黄灯3秒.小明的爸爸随机地由南往北开车经过该路口,问:
(1)他遇到红灯的概率大还是遇到绿灯的概率大?
(2)他遇到红灯的概率是多少?
解:(1)小明的爸爸随机地经过该路口,他每一时刻经过的可能性都相同.因为该路口南北方向红绿灯的设置时间为:红灯40s,绿灯60s,黄灯3s.绿灯时间比红灯时间长,所以他遇到绿灯的概率大.
(2)他遇到红灯的概率为:
1.一儿童行走在如图所示的地板上,当他随意停下时,最终停在地板上阴影部分的概率是( )
A. B. C. D.
A
2.一儿童行走在如图所示的地板上,当他随意停下时,最终停在地板上阴影部分的概率是( )
A. B. C. D.
A
3.在如图所示的正方形纸片上做随机扎针试验,则针头扎在阴影区域内的概率为( )
A. B. C. D.
4.如图,把一个圆形转盘按1∶2∶3∶4的比例分成A、B、C、D四个扇形区域,自由转动转盘,停止后指针落在B区域的概率为________.
5.如图,能自由转动的转盘中, A、B、C、D四个扇形的圆心角的度数分别为180°、 30 °、 60 °、 90 °,转动转盘,当转盘停止时, 指针指向B的概率是_____,指向C或D的概率是_____.
A
B
C
D
6.小明同时抛两枚质地均匀的硬币,出现两个正面朝上的可能性是( )
A.25% B.50% C.75% D.85%
7.中国象棋红方棋按兵种不同分布如下:1个帅,5个兵,“士、象、马、车、炮”各2个,将所有棋子反面朝上放在棋盘上,任取一个不是兵和帅的概率为( )
A. B. C. D.
D
8.如图是一个转盘,扇形1,2,3,4,5所对的圆心角分别是180°,90°,45°,30°,15°,任意转动转盘,求出指针分别指向1,2,3,4,5的概率(指针恰好指向两扇形交线的概率视为零).
9.一张写有密码的纸片被随意地埋在下面矩形区域内(每个格大小相同)
(1)埋在哪个区域的可能性大?
(2)分别计算出埋在三个区域内的概率;
(3)埋在哪两个区域的概率相同.
蓝色
解:
P
(黄色)=
4
1
P
(蓝色)=
2
1
P
(红色)=
4
1
黄色与红色
1. 与面积相关的等可能事件概率的求法:
事件A的概率等于事件A所包含的图形面积m与图形总面积n的比P(A)= .
2.几何面积概率P=
利用此公式时,若所给图形能等分成若干份,可按份数直接计算;若不能,则设法求出各自的面积.
习题6.7
第1、2、3题
6.3 与面积相关的概率
1.了解面积相等的几何概率的计算方法,并能进行简单计算,能设计符合要求的简单概率模型。
2.在具体情境中进一步了解概率的意义,体会概率是描述不确定现象的数学模型。
【教学重点】
会进行简单的概率计算.
【教学难点】
会进行简单的概率计算.
1、摸到红球的概率?
P(摸到红球)=
摸出红球可能出现的结果数
摸出任一球所有可能的结果数
不确定事件发生的可能性
2.事件发生的可能性是有大小的。
必然事件发生的可能性是
1,
不可能事件发生的可能性是
0,
大于0而小于1。
请一位同学在以下8张背面完全相同的扑克牌中任意抽取一张,请问:
P(抽到红心3)= P(抽到黑色)=
P(抽到奇数)= P(抽到黑桃)=
在一些商场中我们可以看到抽奖的转盘,想一想抽中图中各奖励的概率是一样的吗?
如图是卧室与书房地板的示意图,图中每一块方砖除颜色外完全相同.一个小球分别在卧室和书房中自由地滚动,并随机地停留在某块方砖上.
(1)在哪个房间,小球停留在黑砖上的概率大?为什么?
(2)你觉得小球停留在黑砖上的概率大小与什么有关?
(1)在卧室里小球停留在黑砖上的概率大,因为卧室和书房的方砖总块数相等,而卧室的黑砖块数大于书房的黑砖块数,所以在卧室里小球停留在黑砖上的概率大.
(2)与黑砖的块数与方砖总块数的比值的大小有关.
某事件发生的概率等于该事件发生的所有可能结果所组成的图形的面积 SA 与所有可能结果所组成的图形的总面积 S全 的比值.即
与几何图形有关的简单事件发生的概率
如果小球在如图所示的地板上自由地滚动,并随机停留在某块方砖上,它最终停留在黑砖上的概率是多少?
1.题中所说“自由地滚动,并随机停留在某块方砖上”说明了什么?
小球停留在任何一块方砖上的概率都相等.
2.小球停留在方砖上所有可能出现的结果有多少种?停留在黑砖上可能出现的结果有多少种?
小球停留在方砖上所有可能的结果有20种,停留在黑砖上可能出现的结果有5种.
P (小球最终停留在黑砖上)
P (小球最终停留在白砖上) ,
P (小球最终停留在黑砖上) + P (小球最终停留在白砖上) =1 .
3.小球停留在白砖上的概率是多少?它与停留在黑砖上的概率有何关系?
几何概型:
P(A)=
A事件可能出现的结果组成的图形面积(长度或体积)
所有可能出现的结果组成的图形面积(长度或体积)
以几何图形为背景的一种概率模型,在这个模型下,随机试验所有可能的结果发生的概率是相同的.
一般地,在一次试验中,结果落在区域D中每一点都是等可能的,用A表示“试验结果落在D中的一个小区域M中”这个事件,那么事件A发生的概率为
P(A)= .
M的面积(长度或体积)
D的面积(长度或体积)
A事件所占试验区域的份数m
试验区域总份数n
P(A)= .
部分问题可转化为:
D
M
例1.一位汽车司机准备去商场购物,然后他随意把汽车停在某个停车场内,停车场内一个停车位置正好占一个方格且一个方格除颜色外完全一样,则汽车停在红色区域的概率是____.
在上题中,
(1)小球最终停留在白砖上的概率是多少?
(2)小明认为(1)的概率与下面事件发生的概率相等:一个
袋中装有 20 个球,其中有 5 个黑球和 15 个白球,每个球除颜色外都相同,从中任意摸出一个球是白球.
你同意他的想法吗?
等于
P(小球最终停留在白砖上)
(2)同意。因为袋中共有20个球,这些球除颜色外其他都相同,从中任意摸出一个球,这20个球被摸到的概率都相等,所以P(任意摸出一球是白球)
例2.某商场为了吸引顾客,设立了一个可以自由转动的转盘,并规定:顾客每购买 100 元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红、黄或绿色区域, 顾客就可以分别获得 100 元、50 元、20 元的购物券(转盘被等分成 20 个扇形).
甲顾客购物 120 元,他获得购物券的概率是多少?他得到 100元、50元、20元购物券的概率分别是多少?
解:甲顾客的消费额在 100 元到 200 元之间,因此可以获得一次转动转盘的机会.
转盘被等分成 20 个扇形,其中 1 个是红色、2个是黄色、4个是绿色,因此,对于甲顾客来说,
P(获得购物券)
P(获得100元购物券)
P(获得50元购物券)
P(获得20元购物券)
指针不是落在红色区域就是落在白色区域, 落在红色区域和白色区域的概率相等, 所以P(落在红色区域)=
P(落在白色区域)=
如图是一个可以自由转动的转盘, 转动转盘, 当转盘停止时, 指针落在红色区域和白色区域的概率分别是多少?
先把白色区域等分成2份,这样转盘被等分成3个扇形区域,其中1个是红色,2个是白色,所以P(落在红色区域)= ,P(落在白色区域)=
你认为谁做得对?说说你的理由,你是怎样做的?
第2位同学做得对.理由:因为整个圆的圆心角为360°,红色区域扇形的圆心角为120°,则白色区域扇形的圆心角为240°,因此P(落在红色区域)= ,P(落在白色区域)=
例3.某路口南北方向红绿灯的设置时间为:红灯20秒、绿灯60秒、黄灯3秒.小明的爸爸随机地由南往北开车经过该路口,问:
(1)他遇到红灯的概率大还是遇到绿灯的概率大?
(2)他遇到红灯的概率是多少?
解:(1)小明的爸爸随机地经过该路口,他每一时刻经过的可能性都相同.因为该路口南北方向红绿灯的设置时间为:红灯40s,绿灯60s,黄灯3s.绿灯时间比红灯时间长,所以他遇到绿灯的概率大.
(2)他遇到红灯的概率为:
1.一儿童行走在如图所示的地板上,当他随意停下时,最终停在地板上阴影部分的概率是( )
A. B. C. D.
A
2.一儿童行走在如图所示的地板上,当他随意停下时,最终停在地板上阴影部分的概率是( )
A. B. C. D.
A
3.在如图所示的正方形纸片上做随机扎针试验,则针头扎在阴影区域内的概率为( )
A. B. C. D.
4.如图,把一个圆形转盘按1∶2∶3∶4的比例分成A、B、C、D四个扇形区域,自由转动转盘,停止后指针落在B区域的概率为________.
5.如图,能自由转动的转盘中, A、B、C、D四个扇形的圆心角的度数分别为180°、 30 °、 60 °、 90 °,转动转盘,当转盘停止时, 指针指向B的概率是_____,指向C或D的概率是_____.
A
B
C
D
6.小明同时抛两枚质地均匀的硬币,出现两个正面朝上的可能性是( )
A.25% B.50% C.75% D.85%
7.中国象棋红方棋按兵种不同分布如下:1个帅,5个兵,“士、象、马、车、炮”各2个,将所有棋子反面朝上放在棋盘上,任取一个不是兵和帅的概率为( )
A. B. C. D.
D
8.如图是一个转盘,扇形1,2,3,4,5所对的圆心角分别是180°,90°,45°,30°,15°,任意转动转盘,求出指针分别指向1,2,3,4,5的概率(指针恰好指向两扇形交线的概率视为零).
9.一张写有密码的纸片被随意地埋在下面矩形区域内(每个格大小相同)
(1)埋在哪个区域的可能性大?
(2)分别计算出埋在三个区域内的概率;
(3)埋在哪两个区域的概率相同.
蓝色
解:
P
(黄色)=
4
1
P
(蓝色)=
2
1
P
(红色)=
4
1
黄色与红色
1. 与面积相关的等可能事件概率的求法:
事件A的概率等于事件A所包含的图形面积m与图形总面积n的比P(A)= .
2.几何面积概率P=
利用此公式时,若所给图形能等分成若干份,可按份数直接计算;若不能,则设法求出各自的面积.
习题6.7
第1、2、3题
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
