24.1.2弧、弦、圆心角、圆周角
文档属性
| 名称 | 24.1.2弧、弦、圆心角、圆周角 |

|
|
| 格式 | rar | ||
| 文件大小 | 89.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-02 00:00:00 | ||
图片预览

文档简介
24.1.2弧、弦、圆心角、圆周角
一、选择题
1、已知AB、CD是两个不同圆的弦,如AB=CD,那么AB与CD的关系是( )
A、AB=CD B、AB> CD C、 AB< CD D、不能确定
2、如图8,是圆的两条弦,是圆的一条直径,
且平分,下列结论中不一定正确的是( )
A.AB=DB B.BD=CD C. D.
3.在⊙O中,,那么( )
A. B.
C. D.
4.已知⊙O的半径是10cm,是120°,那么弦AB的弦心距是( )
A. 5cm B. C. D.
5、如图,⊙O的直径CD过弦EF的中点G,∠EOD=40°,则∠DCF等于( )
A.80° B. 50° C. 40° D. 20°
6、一个点到圆的最小距离为4cm,最大距离为9cm,则该圆的半径是( )
A、2.5 cm或6.5 cm B、2.5 cm C、6.5 cm D、5 cm或13cm
二、填空题
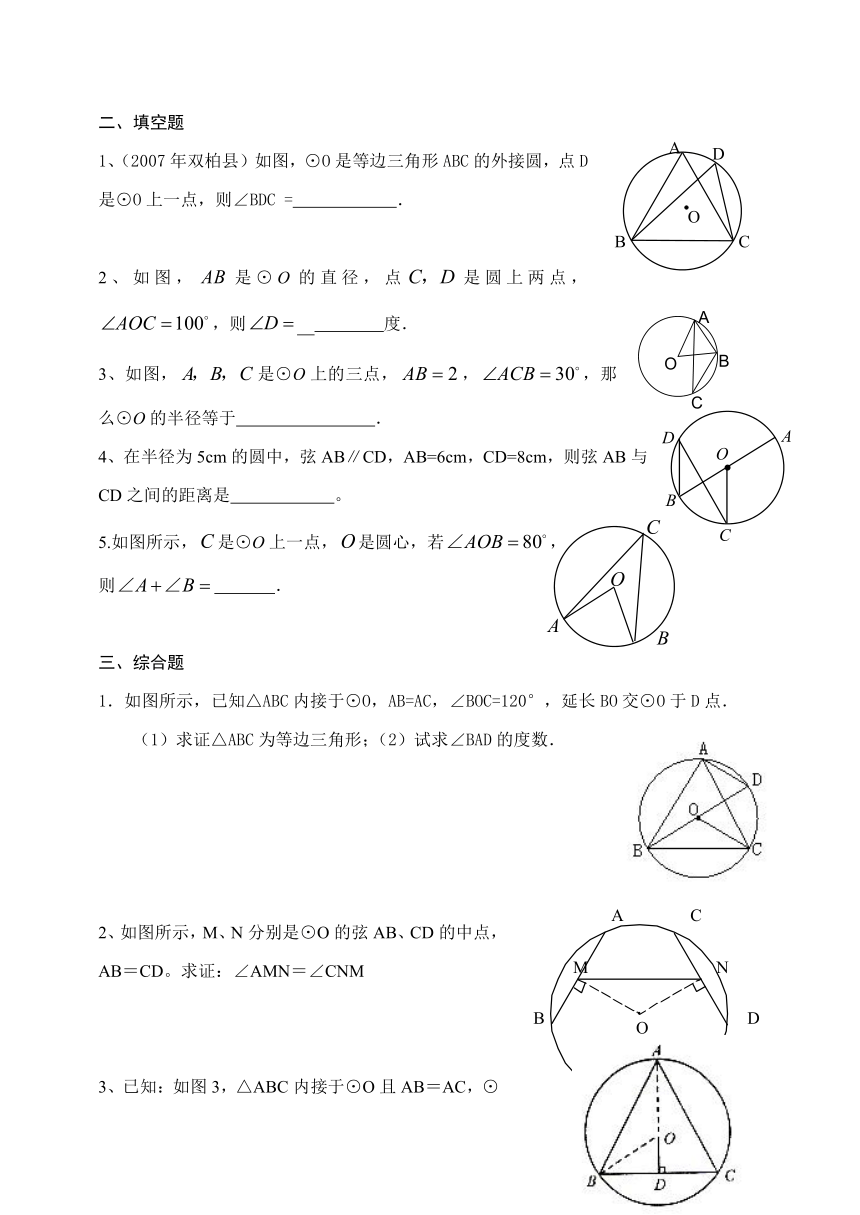
1、(2007年双柏县)如图,⊙O是等边三角形ABC的外接圆,点D是⊙O上一点,则∠BDC = .
2、如图,是⊙O的直径,点是圆上两点,,则 度.
3、如图,是⊙O上的三点,,,那么⊙O的半径等于 .
4、在半径为5cm的圆中,弦AB∥CD,AB=6cm,CD=8cm,则弦AB与CD之间的距离是 。
5.如图所示,是⊙O上一点,是圆心,若,
则 .
三、综合题
1.如图所示,已知△ABC内接于⊙O,AB=AC,∠BOC=120°,延长BO交⊙O于D点.
(1)求证△ABC为等边三角形;(2)试求∠BAD的度数.
2、如图所示,M、N分别是⊙O的弦AB、CD的中点,AB=CD。求证:∠AMN=∠CNM
3、已知:如图3,△ABC内接于⊙O且AB=AC,⊙O的半径等于6cm,O点到BC的距离OD等于2cm,求AB的长。
4、如图,在⊙O中弦AB⊥CD于点E,过E作AC的垂线交BD于点Q,P为垂足,求证Q为BD的中点.
5.如图,点P是圆上的一个动点,弦AB=,PC是∠APB的平分线,∠BAC=30°.
(1)当∠PAC等于多少度时,四边形PACB有最大面积?最大面积是多少?
(2)当∠PAC等于多少度时,四边形PACB是梯形?说明你的理由.
6、如图,在⊙O中,AB是直径,CD是弦,AB⊥CD.
(1)P是上一点(不与C、D重合),求证:∠CPD=∠COB.
(2)点P′在劣弧CD上(不与C、D重合)时,∠CP′D与∠COB有什么数量关系?请证明你的结论.
7.已知多边形ABDEC是由边长为2的等边三角形ABC和正方形BDEC组成,一圆过A、D、E三点,求该圆半径的长.
8、如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10。
(1)求此圆的半径;(2)求图中三角形ADC的面积。
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
B
D
C
A
图8
⌒
⌒
⌒
⌒
D
A
C
B
O
A
O
B
D
C
一、选择题
1、已知AB、CD是两个不同圆的弦,如AB=CD,那么AB与CD的关系是( )
A、AB=CD B、AB> CD C、 AB< CD D、不能确定
2、如图8,是圆的两条弦,是圆的一条直径,
且平分,下列结论中不一定正确的是( )
A.AB=DB B.BD=CD C. D.
3.在⊙O中,,那么( )
A. B.
C. D.
4.已知⊙O的半径是10cm,是120°,那么弦AB的弦心距是( )
A. 5cm B. C. D.
5、如图,⊙O的直径CD过弦EF的中点G,∠EOD=40°,则∠DCF等于( )
A.80° B. 50° C. 40° D. 20°
6、一个点到圆的最小距离为4cm,最大距离为9cm,则该圆的半径是( )
A、2.5 cm或6.5 cm B、2.5 cm C、6.5 cm D、5 cm或13cm
二、填空题
1、(2007年双柏县)如图,⊙O是等边三角形ABC的外接圆,点D是⊙O上一点,则∠BDC = .
2、如图,是⊙O的直径,点是圆上两点,,则 度.
3、如图,是⊙O上的三点,,,那么⊙O的半径等于 .
4、在半径为5cm的圆中,弦AB∥CD,AB=6cm,CD=8cm,则弦AB与CD之间的距离是 。
5.如图所示,是⊙O上一点,是圆心,若,
则 .
三、综合题
1.如图所示,已知△ABC内接于⊙O,AB=AC,∠BOC=120°,延长BO交⊙O于D点.
(1)求证△ABC为等边三角形;(2)试求∠BAD的度数.
2、如图所示,M、N分别是⊙O的弦AB、CD的中点,AB=CD。求证:∠AMN=∠CNM
3、已知:如图3,△ABC内接于⊙O且AB=AC,⊙O的半径等于6cm,O点到BC的距离OD等于2cm,求AB的长。
4、如图,在⊙O中弦AB⊥CD于点E,过E作AC的垂线交BD于点Q,P为垂足,求证Q为BD的中点.
5.如图,点P是圆上的一个动点,弦AB=,PC是∠APB的平分线,∠BAC=30°.
(1)当∠PAC等于多少度时,四边形PACB有最大面积?最大面积是多少?
(2)当∠PAC等于多少度时,四边形PACB是梯形?说明你的理由.
6、如图,在⊙O中,AB是直径,CD是弦,AB⊥CD.
(1)P是上一点(不与C、D重合),求证:∠CPD=∠COB.
(2)点P′在劣弧CD上(不与C、D重合)时,∠CP′D与∠COB有什么数量关系?请证明你的结论.
7.已知多边形ABDEC是由边长为2的等边三角形ABC和正方形BDEC组成,一圆过A、D、E三点,求该圆半径的长.
8、如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10。
(1)求此圆的半径;(2)求图中三角形ADC的面积。
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
B
D
C
A
图8
⌒
⌒
⌒
⌒
D
A
C
B
O
A
O
B
D
C
同课章节目录
