§2.1圆锥曲线课件

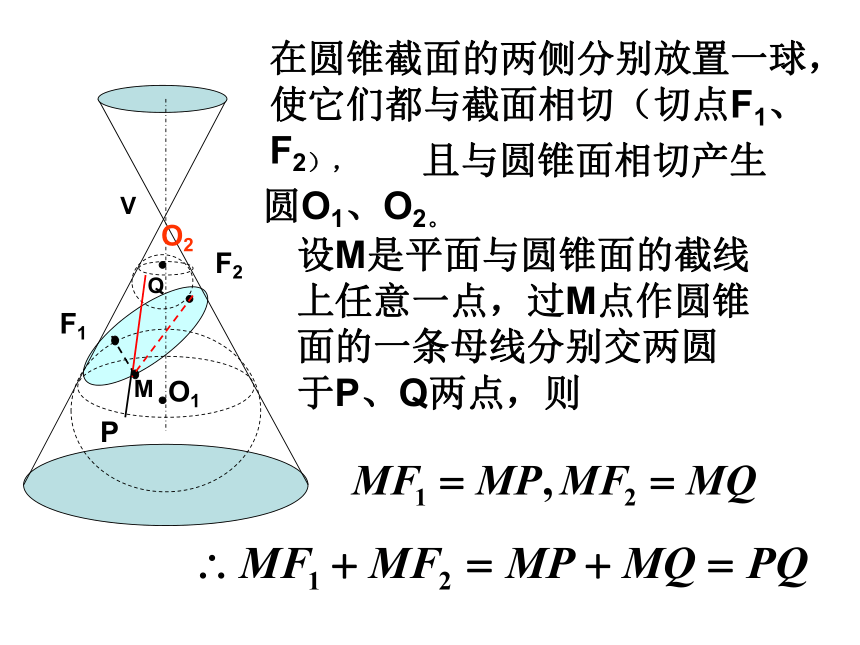
课件11张PPT。圆锥曲线VMO1F1QO2F2P在圆锥截面的两侧分别放置一球，使它们都与截面相切（切点F1、F2）， 且与圆锥面相切产生圆O1、O2。设M是平面与圆锥面的截线上任意一点，过M点作圆锥面的一条母线分别交两圆于P、Q两点，则椭圆的定义 平面内到两定点F1 ，F2的距离之和为常数(大于F1 F2距离）的点的轨迹叫椭圆，两个定点叫椭圆的焦点，两焦点的距离叫做椭圆的焦距双曲线的定义对于第二种情形平面与圆锥的截线由两支曲线
构成，交线上任意一点到平面内两个定点F1，F2的距离的差的绝对值等于常数．
一般的：
平面内两个定点F1，F2的距
离的差的绝对值等于常数
（小于F1、F2）的点的轨
迹叫做双曲线，两个定点
F1，F2叫做双曲线的叫焦点，
两焦点间的距离叫做双曲线
的焦距
平面内与一个定点F和一条定直线l(F不在l）的距离相等的点的轨迹叫做抛物线。
定点F叫做抛物线的焦点。
定直线l 叫做抛物线的准线。 抛物线定义例1：已知B、C是两个定点，BC=4,且⊿ABC的周长等于10。求证：定点A在一个椭圆上。解：如图，BCA练习：
1.平面内到两定点F1(-4,0)、F2(4,0)的距离和等于10的点的轨迹是 （ ）
A. 椭圆 B.双曲线 C. 抛物线 D.线段2.平面内到两定点F1(-1,0)、F2(1,0)的距离的差的绝对值等于2的点的轨迹是 （ ）
A. 椭圆 B.双曲线 C.线段 D.两条射线 3.平面内的点F是定直线L上的一个定点，则到点F和直线L的距离相等的点的轨迹是 （ ）
A. 一个点 B.一条线段 C. 一条射线 D.一条直线ADD4.平面内到点F（0，1）的距离与直线y=-1的距离相等的点的轨迹是____________________
________________________. 以F(0,1)为焦点，直线y=-1为准线的抛物线例2：动圆M过定原C外的一点A,且与圆C外切，问：动圆圆心M的轨迹是什么图形？AMC