2023-2024学年必修二 第十三章 立体几何初步 章节测试题(含答案)
文档属性
| 名称 | 2023-2024学年必修二 第十三章 立体几何初步 章节测试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-09 17:40:45 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2023-2024学年必修二 第十三章 立体几何初步 章节测试题
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1、已知异面直线a,b分别为平面,的垂线,直线m满足,,,,则( )
A.与相交,且交线与m平行 B.与相交,且交线与m垂直
C.与平行,m与平行 D.与平行,m与垂直
2、在底面半径为1的圆柱中,过旋转轴作圆柱的轴截面ABCD,其中母线,E是的中点,F是AB的中点,则( )
A.,AC与EF是共面直线
B.,AC与EF是共面直线
C.,AC与EF是异面直线
D.,AC与EF是异面直线
3、已知某圆锥的侧面展开图是一个半径为的半圆,且该圆锥的体积为,则( )
A. B. C. D.3
4、已知一个圆锥的母线长为2,其侧面积为,则该圆锥的体积为( )
A. B. C. D.
5、今年入夏以来,南方多省市出现高温少雨天气,持续的干旱天气导致多地湖泊及水库水位下降.已知某水库水位为海拔时,相应水面的面积为;水位为海拔时,相应水面的面积为.将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔下降到时,减少的水量约为()( )
A. B. C. D.
6、四面体ABCD顶点都在半径为2的球面上,正三角形ABC的面积为,则四面体ABCD的体积最大为( )
A. B. C. D.
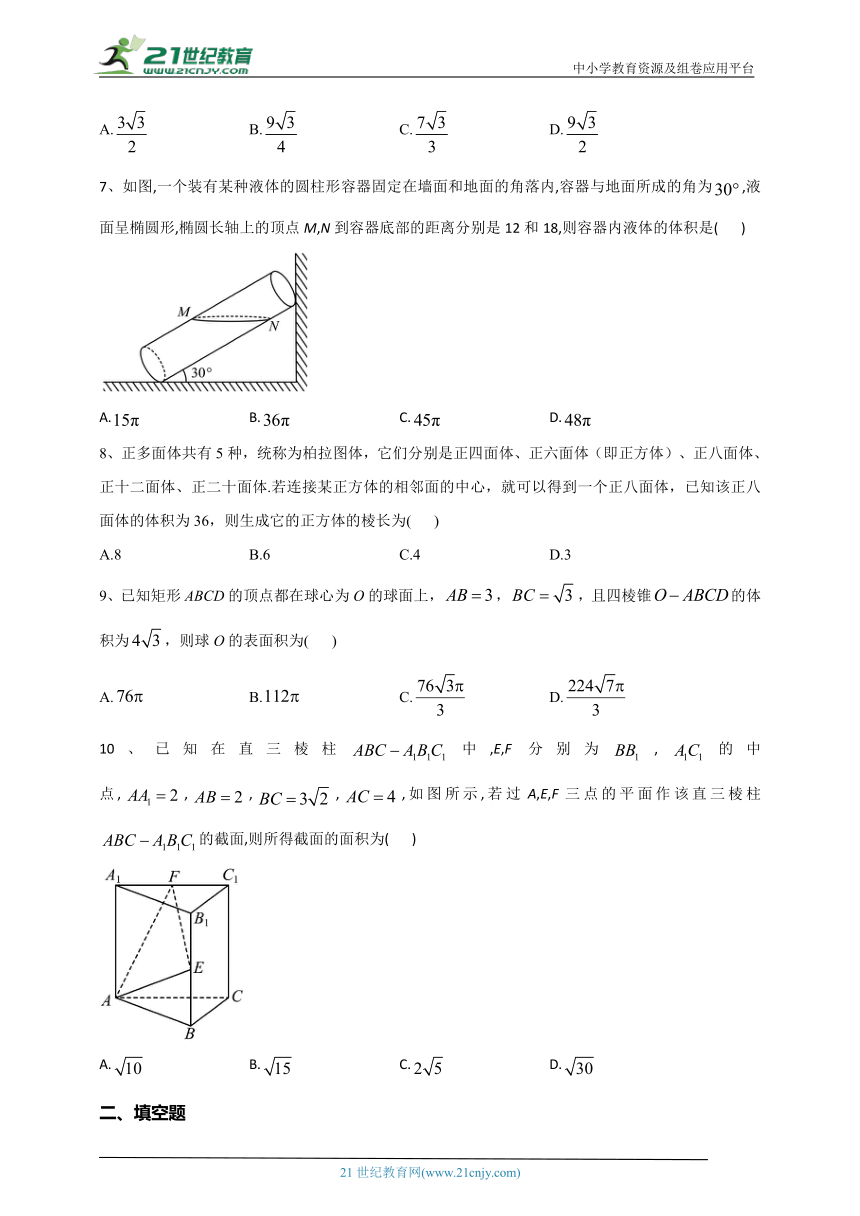
7、如图,一个装有某种液体的圆柱形容器固定在墙面和地面的角落内,容器与地面所成的角为,液面呈椭圆形,椭圆长轴上的顶点M,N到容器底部的距离分别是12和18,则容器内液体的体积是( )
A. B. C. D.
8、正多面体共有5种,统称为柏拉图体,它们分别是正四面体、正六面体(即正方体)、正八面体、正十二面体、正二十面体.若连接某正方体的相邻面的中心,就可以得到一个正八面体,已知该正八面体的体积为36,则生成它的正方体的棱长为( )
A.8 B.6 C.4 D.3
9、已知矩形ABCD的顶点都在球心为O的球面上,,,且四棱锥的体积为,则球O的表面积为( )
A. B. C. D.
10、已知在直三棱柱中,E,F分别为,的中点,,,,,如图所示,若过A,E,F三点的平面作该直三棱柱的截面,则所得截面的面积为( )
A. B. C. D.
二、填空题
11、在四棱锥中,底面ABCD是平行四边形,点M,N分别为棱CD,PC的中点,平面AMN交PB于点F,则___________.
12、《九章算术》中将正四棱台体(棱台的上下底面均为正方形)称为方亭.如图,现有一方亭,其中上底面与下底面的面积之比为,,方亭的四个侧面均为全等的等腰梯形,已知方亭四个侧面的面积之和为,则方亭的体积为______.
13、在空间直角坐标系中,点A,B,C,M的坐标分别是,,,,若A,B,C,M四点共面,则___________.
14、若甲、乙两个圆柱形容器的容积相等,且甲、乙两个圆柱形的容器内部底面半径的比值为2,则甲、乙两个圆柱形容器内部的高度的比值为___________.
15、已知圆柱的底面积为,侧面积为,则该圆柱的体积为____________.
16、已知圆锥表面积为,且它的侧面展开图是一个半圆,则这个圆锥底面半径是__________.
三、解答题
17、在边长为a的正方体上选择四个顶点,然后将它们两两相连,且这四个顶点组成的几何图形为每个面都是等边三角形的四面体,记为四面体.
(1)请在给出的正方体中画出该四面体,并证明;
(2)设的中心为O,关于点O的对称的四面体记为,求与的公共部分的体积.(注:到各个顶点距离相等的点称为四面体的中心)
18、如图,四棱锥中,为正三角形,为正方形,平面平面,E、F分别为、中点.
(1)证明:平面;
(2)求直线与平面所成角的正弦值.
19、如图,在四棱锥中,底面ABCD是正方形,底面ABCD,,O为AC与BD的交点.
(1)证明:平面PAC.
(2)若M为PD的中点,求三棱锥的体积.
20、如图,在直棱柱ABCD-EFGH中,底面ABCD是边长为2的正方形,N是CG上的一点平面FHN.
(1)请确定点N的位置;
(2)若直线BG与平面FHN所成的角为求AE.
参考答案
1、答案:A
解析:若与平行,由,可得,与条件矛盾,不符合题意,故C,D错误;
所以与相交,如图所示,作,且与直线a相交,
设,a,,则由题意,故,同理,
因为,,所以,故A正确.
2、答案:D
解析:连结BE,CE,如图,
易知BC是圆O的直径,所以,又因为E是的中点,故,
所以在等腰中,,则,
因为AB是圆柱的母线,所以面,又BE,面BCE,故,,
所以在中,,
在中,由F是AB的中点得,故,所以,
可以看到,面,面,由异面直线的定义可知,AC与EF是异面直线.
故选:D.
3、答案:C
解析:令圆锥底面圆半径为,则,解得,
从而圆锥的高,
因此圆锥的体积,解得.
故选:C
4、答案:A
解析:设圆锥的底面半径为r,高为h,母线长为,
由,则,
则圆锥的体积为.
故选:A
5、答案:C
解析:台体体积公式:,
由题意可得,
代入计算得
故选:C.
6、答案:B
解析:设正三角形ABC的边长为a,,
所以,
由正弦定理(r为的外接圆的半径)
所以,
所以球心到平面ABC的距离,
则四面体体积最大为.
故选:B
7、答案:C
解析:如图为圆柱的轴截面图,过M作容器壁的垂线,垂足为F,
因为MN平行于地面,故,
椭圆长轴上的顶点M,N到容器底部的距离分别是12和18,
故,
在中,,即圆柱的底面半径为,
所以容器内液体的体积等于一个底面半径为,高为的圆柱体积的一半,
即为,
故选:C.
8、答案:B
解析:设正方体棱长为,可得正八面体是由两个四棱锥构成,
四棱锥的底面为边长为的正方形,高为a,
则正八面体体积为,解得,.
故选:B.
9、答案:A
解析:由题可知矩形ABCD所在截面圆的半径即为矩形ABCD的对角线长度的一半,因为,,所以矩形ABCD所在截面圆的半径,由矩形ABCD的面积,设O到平面ABCD的距离为h,所以,解得,所以球O的半径,所以球O的表面积.故选A.
10、答案:B
解析:延长AF,且AF与相交于G,连接EG,并与相交于D,连接FD,则四边形AEDF为所求的截面.
在中,由,,得.
在中,由,,得.
因为F为的中点,所以由平面几何知识可知,.
所以,,即G为AG的中点,所以.
又由,可得,
又,,所以.
在中,由,,得,所以.
所以在中,有,,,
即,所以.又注意到,
,
则四边形AEDF的面积为.
故选:B.
11、答案:或1:12
解析:延长BC,交AM的延长线于点E,连接EN并延长,交BP于点F,连接AF,
因为M为CD中点,由三角形相似可得:,
即C为BE中点,
设
因为N是PC中点,
所以
,
因为F,N,E三点共线,所以存在a使得,即,
整理得,其中,
所以,解得:,
所以.
故答案为:
12、答案:
解析:由题意得,设,则,.
过点E,F在平面ABFE内分别作,,垂足分别为点M,N,
在等腰梯形ABFE中,因为,,,则四边形MNFE为矩形,
所以,,则,
因为,,,
所以,所以,
在中,由勾股定理得,
所以等腰梯形ABFE的面积为,所以.
所以,,方亭的高,
故方亭的体积为.
故答案为:
13、答案:6
解析:由题意,得,,,
又A,B,C,M四点共面,则存在x,,使得,
即,即,解得,
所以.
故答案为:6.
14、答案:
解析:由圆柱形容器的容积,得,所以甲、乙两个圆柱形容器内部的高度的比值为.
15、答案:
解析:设圆柱的底面半径为r,高为h,由已知可得,,
,
该圆柱的体积为.
故答案为:.
16、答案:
解析:设圆锥的底面半径为r,母线长为l,
因为圆锥的表面积为,
所以,即,
又圆锥的侧面展开图是一个半圆,
所以,即,
所以.
故答案为:.
17、答案:(1)见解析
(2)
解析:(1)如图,取A,,C,四点并顺次连接四点,
构成四面体,
设正方体的边长为a,
则该四面体的每一条边长为,
所以证得四面体为正四面体;
(2)连接,交于点O,
则O为正方体的中心,
所以O到正方体的各个顶点的距离相等,
故O为四面体的中心,
可得A关于O的对称点为,关于O的对称点为D,
C关于O的对称点为,关于O的对称点为B,
如图所示,得到四面体为,
,
设,,分别为CA,,的中点,
所以.
18、
(1)答案:见解析
解析:连接,
是正方形,E是的中点,
E是的中点,F是的中点,
,平面,平面,
平面.
(2)答案:
解析:建立如图所示空间直角坐标系,设,
则,,,,
,,,
设平面的法向量,则,
取得,设与平面所成角为,
则.
19、答案:(1)见解析
(2)
解析:(1)证明:底面ABCD,
.
底面ABCD是正方形,
.
PA,平面PAC.,
平面PAC.
(2)O为AC与BD的交点,
O为AC与BD的中点,
.
M为PD的中点,点M到平面OCD的距离为.
20、答案:(1)点N为CG的中点
(2)或
解析:(1)
如图,连接EG与HF相交于点O,
平面平面,
平面FHN,平面FHN,平面FHN,
,
为正方形EFGH的对角线的交点,,,
,,,
点N为CG的中点;
(2)设,如图,连接ON,记FN和BG的交点为T,过点G作ON的垂线,垂足为P,连接PT,四边形EFGH为正方形,O为对角线的交点,,
,,,,
,,,
,,OG,平面OGN,,平面OGN,
平面OGN,平面OGN,,
,,FH,平面FHN,,平面FHN,
平面FHN,直线BG与平面FHN所成的角的平面角为,
,
在正方形EFGH中,由,可得.
在中,,有,在长方形BCGF中,由,,有,
可得,
在中,,
又由,有,解得或,故或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年必修二 第十三章 立体几何初步 章节测试题
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1、已知异面直线a,b分别为平面,的垂线,直线m满足,,,,则( )
A.与相交,且交线与m平行 B.与相交,且交线与m垂直
C.与平行,m与平行 D.与平行,m与垂直
2、在底面半径为1的圆柱中,过旋转轴作圆柱的轴截面ABCD,其中母线,E是的中点,F是AB的中点,则( )
A.,AC与EF是共面直线
B.,AC与EF是共面直线
C.,AC与EF是异面直线
D.,AC与EF是异面直线
3、已知某圆锥的侧面展开图是一个半径为的半圆,且该圆锥的体积为,则( )
A. B. C. D.3
4、已知一个圆锥的母线长为2,其侧面积为,则该圆锥的体积为( )
A. B. C. D.
5、今年入夏以来,南方多省市出现高温少雨天气,持续的干旱天气导致多地湖泊及水库水位下降.已知某水库水位为海拔时,相应水面的面积为;水位为海拔时,相应水面的面积为.将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔下降到时,减少的水量约为()( )
A. B. C. D.
6、四面体ABCD顶点都在半径为2的球面上,正三角形ABC的面积为,则四面体ABCD的体积最大为( )
A. B. C. D.
7、如图,一个装有某种液体的圆柱形容器固定在墙面和地面的角落内,容器与地面所成的角为,液面呈椭圆形,椭圆长轴上的顶点M,N到容器底部的距离分别是12和18,则容器内液体的体积是( )
A. B. C. D.
8、正多面体共有5种,统称为柏拉图体,它们分别是正四面体、正六面体(即正方体)、正八面体、正十二面体、正二十面体.若连接某正方体的相邻面的中心,就可以得到一个正八面体,已知该正八面体的体积为36,则生成它的正方体的棱长为( )
A.8 B.6 C.4 D.3
9、已知矩形ABCD的顶点都在球心为O的球面上,,,且四棱锥的体积为,则球O的表面积为( )
A. B. C. D.
10、已知在直三棱柱中,E,F分别为,的中点,,,,,如图所示,若过A,E,F三点的平面作该直三棱柱的截面,则所得截面的面积为( )
A. B. C. D.
二、填空题
11、在四棱锥中,底面ABCD是平行四边形,点M,N分别为棱CD,PC的中点,平面AMN交PB于点F,则___________.
12、《九章算术》中将正四棱台体(棱台的上下底面均为正方形)称为方亭.如图,现有一方亭,其中上底面与下底面的面积之比为,,方亭的四个侧面均为全等的等腰梯形,已知方亭四个侧面的面积之和为,则方亭的体积为______.
13、在空间直角坐标系中,点A,B,C,M的坐标分别是,,,,若A,B,C,M四点共面,则___________.
14、若甲、乙两个圆柱形容器的容积相等,且甲、乙两个圆柱形的容器内部底面半径的比值为2,则甲、乙两个圆柱形容器内部的高度的比值为___________.
15、已知圆柱的底面积为,侧面积为,则该圆柱的体积为____________.
16、已知圆锥表面积为,且它的侧面展开图是一个半圆,则这个圆锥底面半径是__________.
三、解答题
17、在边长为a的正方体上选择四个顶点,然后将它们两两相连,且这四个顶点组成的几何图形为每个面都是等边三角形的四面体,记为四面体.
(1)请在给出的正方体中画出该四面体,并证明;
(2)设的中心为O,关于点O的对称的四面体记为,求与的公共部分的体积.(注:到各个顶点距离相等的点称为四面体的中心)
18、如图,四棱锥中,为正三角形,为正方形,平面平面,E、F分别为、中点.
(1)证明:平面;
(2)求直线与平面所成角的正弦值.
19、如图,在四棱锥中,底面ABCD是正方形,底面ABCD,,O为AC与BD的交点.
(1)证明:平面PAC.
(2)若M为PD的中点,求三棱锥的体积.
20、如图,在直棱柱ABCD-EFGH中,底面ABCD是边长为2的正方形,N是CG上的一点平面FHN.
(1)请确定点N的位置;
(2)若直线BG与平面FHN所成的角为求AE.
参考答案
1、答案:A
解析:若与平行,由,可得,与条件矛盾,不符合题意,故C,D错误;
所以与相交,如图所示,作,且与直线a相交,
设,a,,则由题意,故,同理,
因为,,所以,故A正确.
2、答案:D
解析:连结BE,CE,如图,
易知BC是圆O的直径,所以,又因为E是的中点,故,
所以在等腰中,,则,
因为AB是圆柱的母线,所以面,又BE,面BCE,故,,
所以在中,,
在中,由F是AB的中点得,故,所以,
可以看到,面,面,由异面直线的定义可知,AC与EF是异面直线.
故选:D.
3、答案:C
解析:令圆锥底面圆半径为,则,解得,
从而圆锥的高,
因此圆锥的体积,解得.
故选:C
4、答案:A
解析:设圆锥的底面半径为r,高为h,母线长为,
由,则,
则圆锥的体积为.
故选:A
5、答案:C
解析:台体体积公式:,
由题意可得,
代入计算得
故选:C.
6、答案:B
解析:设正三角形ABC的边长为a,,
所以,
由正弦定理(r为的外接圆的半径)
所以,
所以球心到平面ABC的距离,
则四面体体积最大为.
故选:B
7、答案:C
解析:如图为圆柱的轴截面图,过M作容器壁的垂线,垂足为F,
因为MN平行于地面,故,
椭圆长轴上的顶点M,N到容器底部的距离分别是12和18,
故,
在中,,即圆柱的底面半径为,
所以容器内液体的体积等于一个底面半径为,高为的圆柱体积的一半,
即为,
故选:C.
8、答案:B
解析:设正方体棱长为,可得正八面体是由两个四棱锥构成,
四棱锥的底面为边长为的正方形,高为a,
则正八面体体积为,解得,.
故选:B.
9、答案:A
解析:由题可知矩形ABCD所在截面圆的半径即为矩形ABCD的对角线长度的一半,因为,,所以矩形ABCD所在截面圆的半径,由矩形ABCD的面积,设O到平面ABCD的距离为h,所以,解得,所以球O的半径,所以球O的表面积.故选A.
10、答案:B
解析:延长AF,且AF与相交于G,连接EG,并与相交于D,连接FD,则四边形AEDF为所求的截面.
在中,由,,得.
在中,由,,得.
因为F为的中点,所以由平面几何知识可知,.
所以,,即G为AG的中点,所以.
又由,可得,
又,,所以.
在中,由,,得,所以.
所以在中,有,,,
即,所以.又注意到,
,
则四边形AEDF的面积为.
故选:B.
11、答案:或1:12
解析:延长BC,交AM的延长线于点E,连接EN并延长,交BP于点F,连接AF,
因为M为CD中点,由三角形相似可得:,
即C为BE中点,
设
因为N是PC中点,
所以
,
因为F,N,E三点共线,所以存在a使得,即,
整理得,其中,
所以,解得:,
所以.
故答案为:
12、答案:
解析:由题意得,设,则,.
过点E,F在平面ABFE内分别作,,垂足分别为点M,N,
在等腰梯形ABFE中,因为,,,则四边形MNFE为矩形,
所以,,则,
因为,,,
所以,所以,
在中,由勾股定理得,
所以等腰梯形ABFE的面积为,所以.
所以,,方亭的高,
故方亭的体积为.
故答案为:
13、答案:6
解析:由题意,得,,,
又A,B,C,M四点共面,则存在x,,使得,
即,即,解得,
所以.
故答案为:6.
14、答案:
解析:由圆柱形容器的容积,得,所以甲、乙两个圆柱形容器内部的高度的比值为.
15、答案:
解析:设圆柱的底面半径为r,高为h,由已知可得,,
,
该圆柱的体积为.
故答案为:.
16、答案:
解析:设圆锥的底面半径为r,母线长为l,
因为圆锥的表面积为,
所以,即,
又圆锥的侧面展开图是一个半圆,
所以,即,
所以.
故答案为:.
17、答案:(1)见解析
(2)
解析:(1)如图,取A,,C,四点并顺次连接四点,
构成四面体,
设正方体的边长为a,
则该四面体的每一条边长为,
所以证得四面体为正四面体;
(2)连接,交于点O,
则O为正方体的中心,
所以O到正方体的各个顶点的距离相等,
故O为四面体的中心,
可得A关于O的对称点为,关于O的对称点为D,
C关于O的对称点为,关于O的对称点为B,
如图所示,得到四面体为,
,
设,,分别为CA,,的中点,
所以.
18、
(1)答案:见解析
解析:连接,
是正方形,E是的中点,
E是的中点,F是的中点,
,平面,平面,
平面.
(2)答案:
解析:建立如图所示空间直角坐标系,设,
则,,,,
,,,
设平面的法向量,则,
取得,设与平面所成角为,
则.
19、答案:(1)见解析
(2)
解析:(1)证明:底面ABCD,
.
底面ABCD是正方形,
.
PA,平面PAC.,
平面PAC.
(2)O为AC与BD的交点,
O为AC与BD的中点,
.
M为PD的中点,点M到平面OCD的距离为.
20、答案:(1)点N为CG的中点
(2)或
解析:(1)
如图,连接EG与HF相交于点O,
平面平面,
平面FHN,平面FHN,平面FHN,
,
为正方形EFGH的对角线的交点,,,
,,,
点N为CG的中点;
(2)设,如图,连接ON,记FN和BG的交点为T,过点G作ON的垂线,垂足为P,连接PT,四边形EFGH为正方形,O为对角线的交点,,
,,,,
,,,
,,OG,平面OGN,,平面OGN,
平面OGN,平面OGN,,
,,FH,平面FHN,,平面FHN,
平面FHN,直线BG与平面FHN所成的角的平面角为,
,
在正方形EFGH中,由,可得.
在中,,有,在长方形BCGF中,由,,有,
可得,
在中,,
又由,有,解得或,故或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
