镶嵌

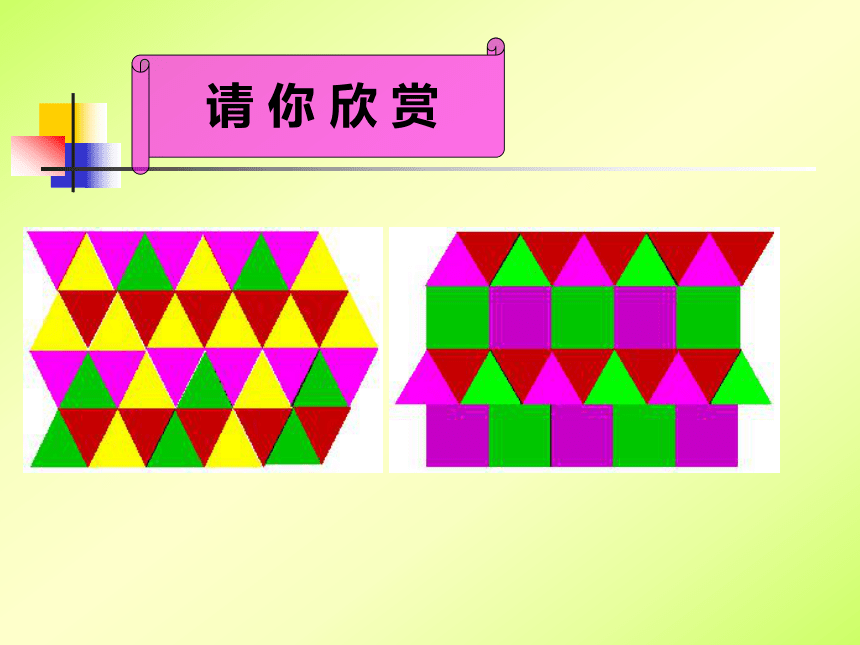
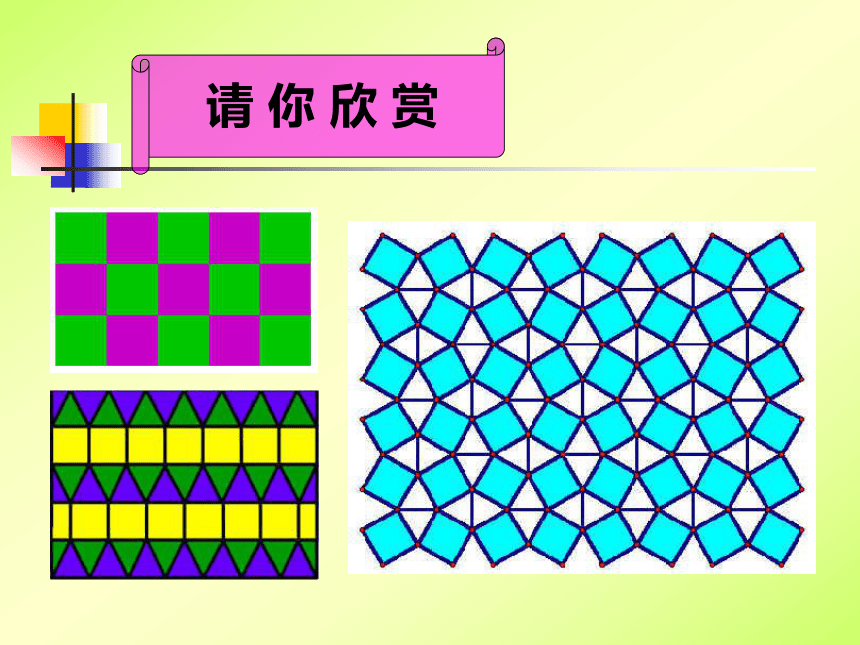
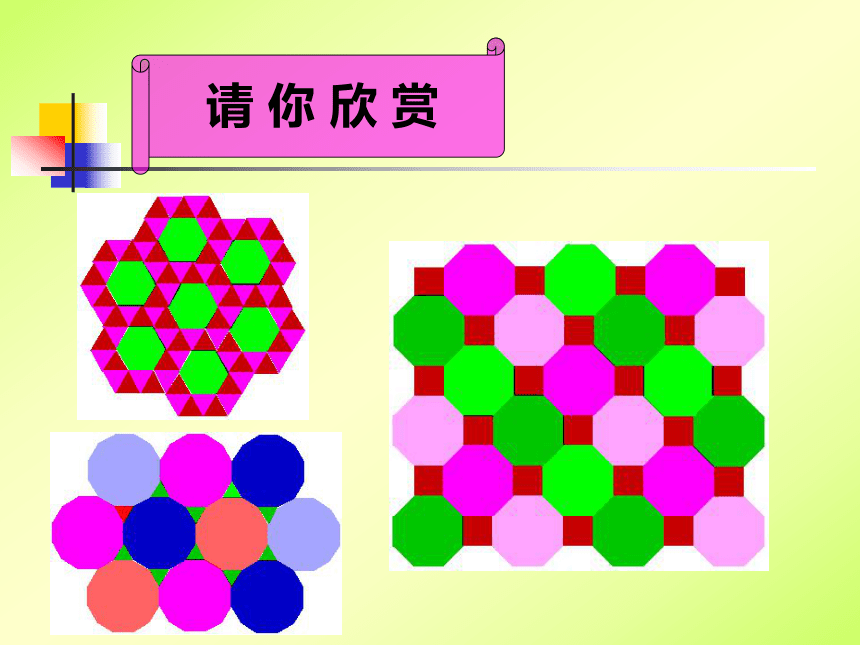
课件26张PPT。7.4 课题学习—镶嵌请 你 欣 赏请 你 欣 赏请 你 欣 赏请 你 欣 赏 教 师 寄 语 每天当我们走到街上， 或者我们家庭装修房子时都会看到各种图案的地砖。同学们是否注意到这些图案是由哪些几何图形拼成的？你们知道为什么这些几何图形能铺满整个地面呢? 看来地砖中蕴含着丰富的数学问题.同学们,通过这节课的学习，相信你们一定能从中知道地砖中的学问!

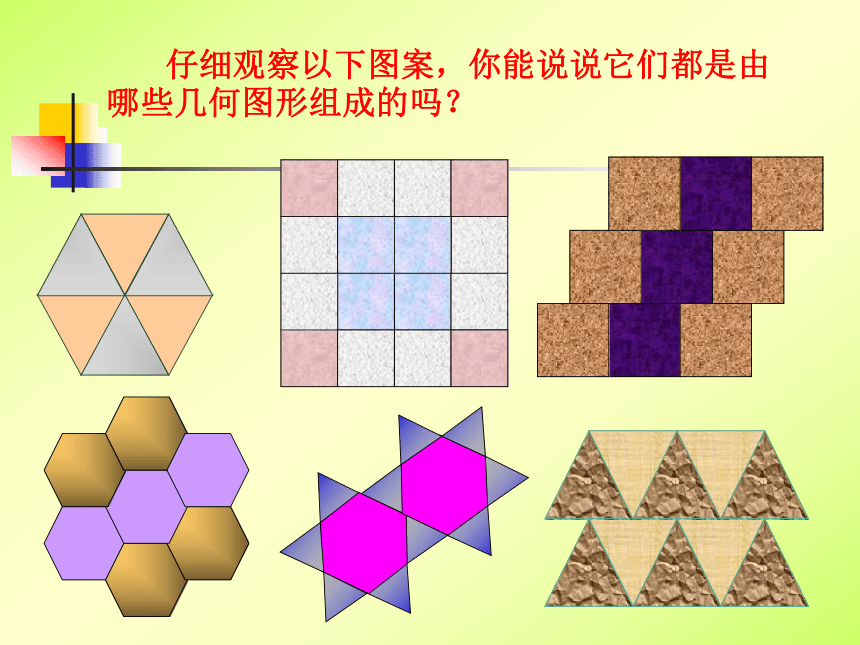
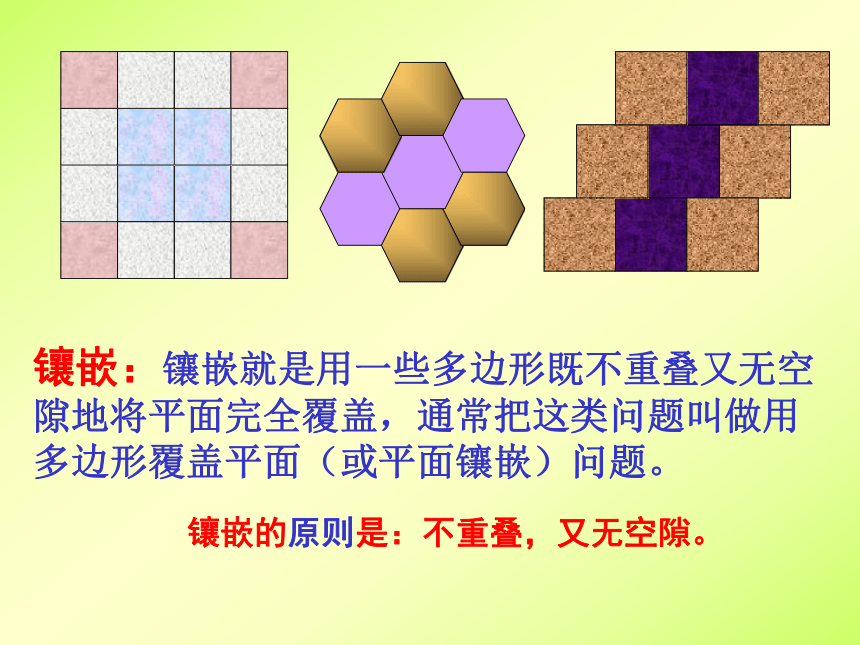
仔细观察以下图案，你能说说它们都是由哪些几何图形组成的吗？镶嵌：镶嵌就是用一些多边形既不重叠又无空隙地将平面完全覆盖，通常把这类问题叫做用多边形覆盖平面（或平面镶嵌）问题。
镶嵌的原则是：不重叠，又无空隙。 1、请同学们拿出准备好的正多边形纸片以小组为单位，试一试，用同一种正多边形（如正三角形，正四边形，正六边形）能否镶嵌成平面图案? 如果能 , 共有几种正多边形能镶嵌成平面图案呢 ? 完成后请将你的作品展示到黑板上。
2、可以拼成一个平面条件是什么？
60°60°60°60°60°60° 每个顶点由6个正三角形依次环绕而成.（3，3，3，3，3，3）（1)正三角形的平面镶嵌结论：用边长相同的正三角形可以镶嵌.90° 每个顶点由4个正方形依次环绕而成.（4，4，4，4）90°90°90°（2）正方形的平面镶嵌结论：用边长相同的正方形可以镶嵌.120 °120 °120 °每个顶点由3个正六边形依次环绕而成.（6，6，6）（3）正六边形的平面镶嵌结论：用边长相同的正六边形可以镶嵌.
请同学们拿出准备好的正五边形纸片，试一试能否镶嵌成平面图案，为什么？
啊!拼不了啦,为什么呢?你能说说道理吗?123∠1+∠2+∠3=?（4）正五边形能否平面镶嵌？结论：用边长相同的正五边形不能镶嵌.镶嵌平面图案需要的什么条件？
1.拼接在同一个点的各个角的和恰好等于360度；
2.相邻的多边形有公共边.想一想诀窍：看某种正多边形的一个内角度数的倍数是否为360°,若是则这种正多边形就能镶嵌。6433能拼好能拼好不能拼好
有缺口能拼好 剪出一些形状、大小完全相同的任意三角形纸板，拼拼看，它们能否镶嵌成平面图案？结论：形状、大小完全相同的任意三角形纸板，
它们能镶嵌成平面图案. 剪出一些形状、大小完全相同的任意四边形纸板，拼拼看，它们能否镶嵌成平面图案？结论：形状、大小完全相同的任意四边形纸板，
它们能镶嵌成平面图案.正三角形正方形正六边形正八边形 当围绕一点拼在一起的两种正多边形的内角加在一起恰好组成一个周角时，这两种正多边形就能镶嵌.规律： 当围绕一点拼在一起的几种正多边形的内角加在一起恰好组成一个周角时，这几种正多边形就能镶嵌.学以致用请你创造美成果展示4、 下列正多边形的组合中 , 不能镶嵌的是 ( ) A. 正方形和正三角形 ? B. 正方形和正八边形 C. 正三角形和正十二边形 D. 正方形和正六边形 1、下列正多边形不能够镶嵌成平面图案的是 (? ) A. 正三角形 ? B. 正方形 C .正五边形 ?D. 正六边形 2、用正方形一种图形进行平面镶嵌时，在它的一个顶点周围的
正方形的个数是（ ）
A. 3 B .4 C.5 D .63、如果只用一种正多边形作平面镶嵌，而且在每一个正多边形
的每一个顶点周围都有6个正多边形，则该正多边形的内角度数
为（ ）
A.120 0 B.90 0 C.60 0 D.450知识检测：CCBD 本节课我们通过活动，探讨，知道任意一个三角形，四边形或正六边形可以镶嵌成一个平面，并且探索出正多边形镶嵌的条件．即：一种正多边形的一个内角的倍数是否是360° 课堂小结谢谢合作
再见

二00八年四月