27.2三角形的相似判定2
文档属性
| 名称 | 27.2三角形的相似判定2 |

|
|
| 格式 | rar | ||
| 文件大小 | 128.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-12-16 00:00:00 | ||
图片预览

文档简介
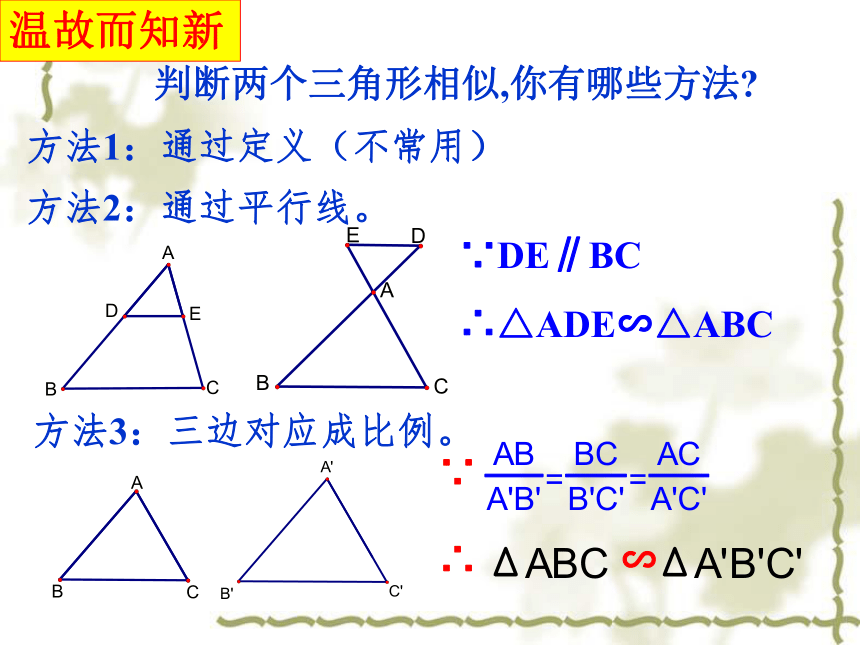
课件11张PPT。27.2 相似三角形的判定2判断两个三角形相似,你有哪些方法?方法1:通过定义(不常用)方法2:通过平行线。方法3:三边对应成比例。温故而知新∵DE∥BC
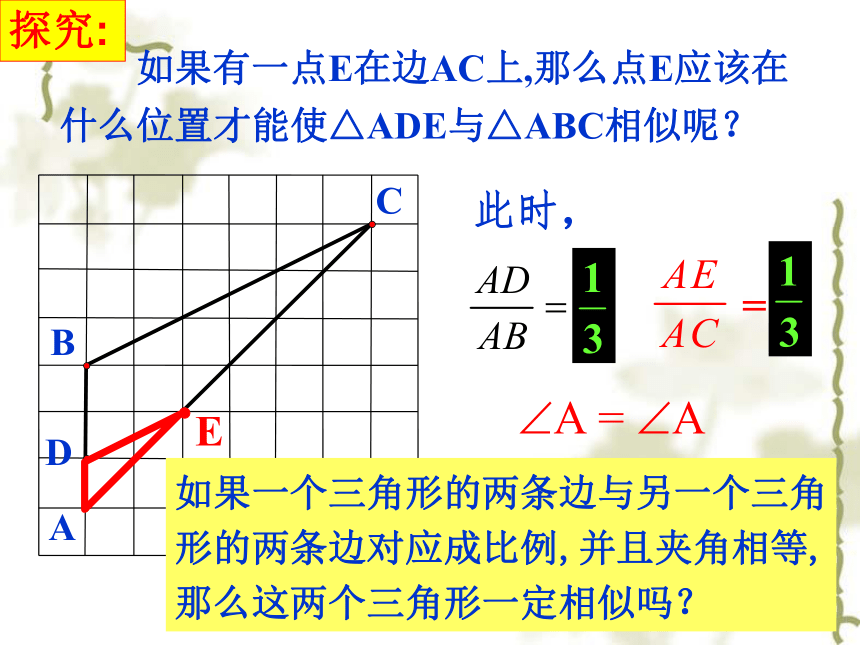
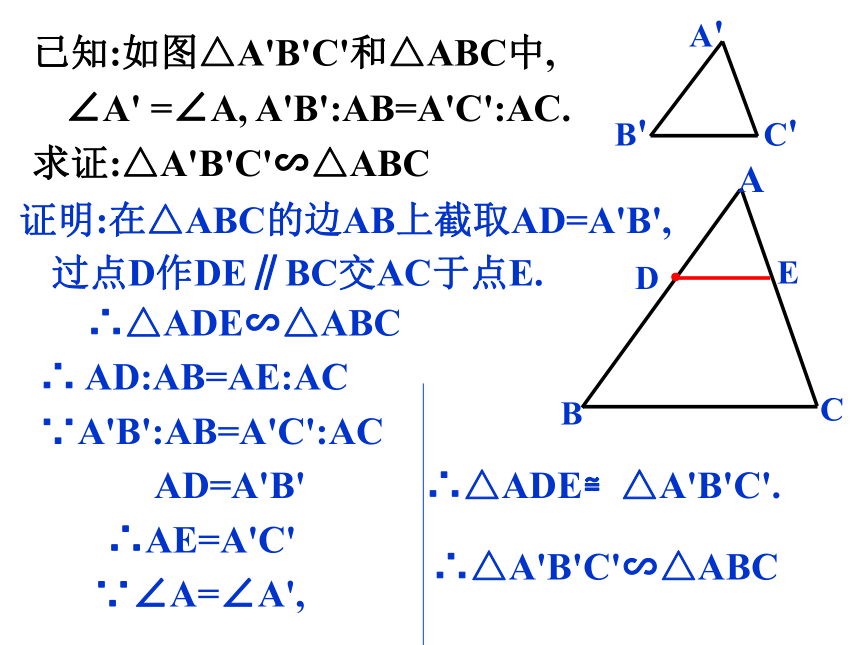
∴△ADE∽△ABC 如果有一点E在边AC上,那么点E应该在什么位置才能使△ADE与△ABC相似呢? 此时,如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形一定相似吗? 探究:证明:在△ABC的边AB上截取AD=A'B',过点D作DE∥BC交AC于点E.已知:如图△A'B'C'和△ABC中, ∠A' =∠A, A'B':AB=A'C':AC.
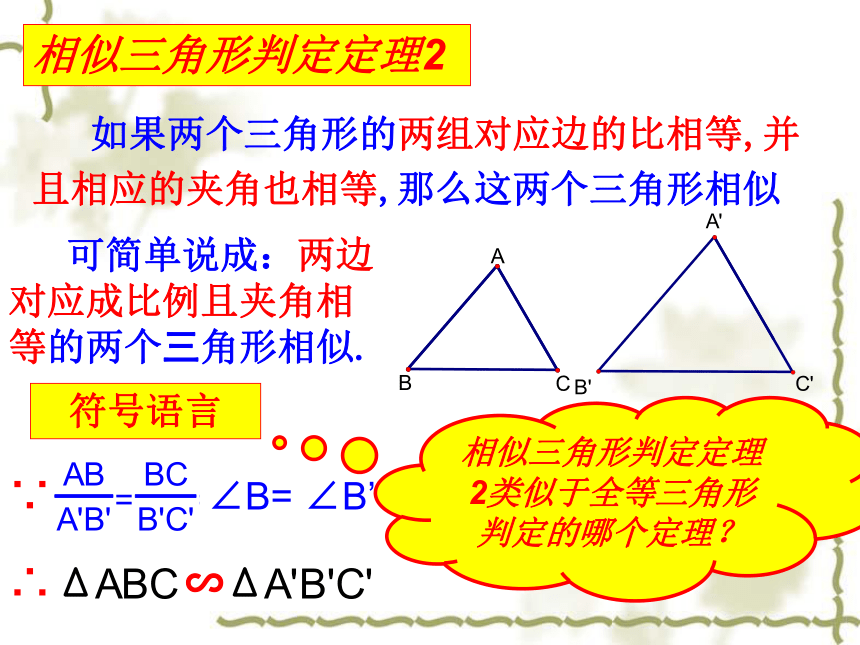
求证:△A'B'C'∽△ABCABCED·∵A'B':AB=A'C':AC ∵∠A=∠A',∴△ADE≌△A'B'C'.∴ AD:AB=AE:AC∴△ADE∽△ABC∴△A'B'C'∽△ABCAD=A'B'∴AE=A'C'相似三角形判定定理2 如果两个三角形的两组对应边的比相等,并且相应的夹角也相等,那么这两个三角形相似符号语言相似三角形判定定理2类似于全等三角形判定的哪个定理? 可简单说成:两边对应成比例且夹角相等的两个三角形相似.相似三角形判定定理2 如果两个三角形的两组对应边的比相等,并且相应的夹角也相等,那么这两个三角形相似此角如果不是两边夹角,两三角形还相似吗?学习例题例1:根据下列条件,判断△ABC与△A’B’C’是否相似,并说明理由。∠A=120°, AB=7cm, AC=14cm
∠A’=120°, A’B’=3cm, A’C’=6cm(2) AB=4cm, AB=6cm, AC=8cm
A’B’=12cm,A’B’=18cm,A’C’=21cm相似不相似121.如图,已知∠1= ∠2,那么添加下列_____条件后,能判定△ABC∽△ADE
① ②练习:① 2.判断图中△AEB和△FEC是否相似?并说明理由。 例2:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点,
求证:△ADQ∽△QCP练习1.如图,已知△ABC∽△ADE.求证:△ABD∽△ACE2.已知:如图,BD、CE是△ABC的高,
试说明△ADE∽△ABC。这节课你学到了什么??平行于三角形一边的直线与其他两边(或延长线)相交,所构成的三角形与原三角形相似;?三边对应成比例,两三角形相似.相似三角形的判定方法:?两边对应成比例且夹角相等,两三角形相似.
∴△ADE∽△ABC 如果有一点E在边AC上,那么点E应该在什么位置才能使△ADE与△ABC相似呢? 此时,如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形一定相似吗? 探究:证明:在△ABC的边AB上截取AD=A'B',过点D作DE∥BC交AC于点E.已知:如图△A'B'C'和△ABC中, ∠A' =∠A, A'B':AB=A'C':AC.
求证:△A'B'C'∽△ABCABCED·∵A'B':AB=A'C':AC ∵∠A=∠A',∴△ADE≌△A'B'C'.∴ AD:AB=AE:AC∴△ADE∽△ABC∴△A'B'C'∽△ABCAD=A'B'∴AE=A'C'相似三角形判定定理2 如果两个三角形的两组对应边的比相等,并且相应的夹角也相等,那么这两个三角形相似符号语言相似三角形判定定理2类似于全等三角形判定的哪个定理? 可简单说成:两边对应成比例且夹角相等的两个三角形相似.相似三角形判定定理2 如果两个三角形的两组对应边的比相等,并且相应的夹角也相等,那么这两个三角形相似此角如果不是两边夹角,两三角形还相似吗?学习例题例1:根据下列条件,判断△ABC与△A’B’C’是否相似,并说明理由。∠A=120°, AB=7cm, AC=14cm
∠A’=120°, A’B’=3cm, A’C’=6cm(2) AB=4cm, AB=6cm, AC=8cm
A’B’=12cm,A’B’=18cm,A’C’=21cm相似不相似121.如图,已知∠1= ∠2,那么添加下列_____条件后,能判定△ABC∽△ADE
① ②练习:① 2.判断图中△AEB和△FEC是否相似?并说明理由。 例2:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点,
求证:△ADQ∽△QCP练习1.如图,已知△ABC∽△ADE.求证:△ABD∽△ACE2.已知:如图,BD、CE是△ABC的高,
试说明△ADE∽△ABC。这节课你学到了什么??平行于三角形一边的直线与其他两边(或延长线)相交,所构成的三角形与原三角形相似;?三边对应成比例,两三角形相似.相似三角形的判定方法:?两边对应成比例且夹角相等,两三角形相似.
