24.1.2垂径定理1

课件13张PPT。24.1.2 垂径定理　把一个圆沿着它的任意一条直径对折，重复几次，你发现了什么？由此你能得到什么结论？可以发现：
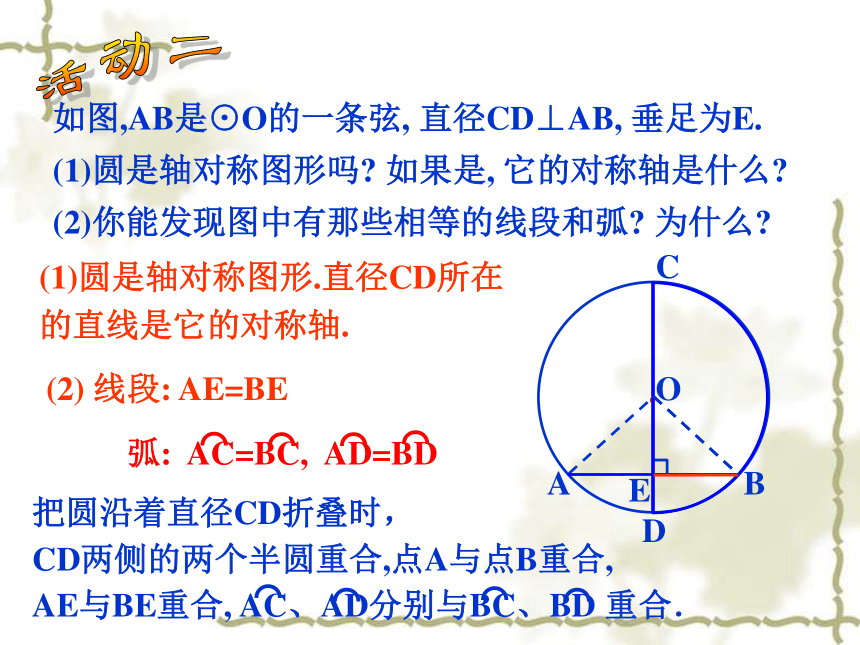
圆是轴对称图形，任何一条直径所在直线都是它的对称轴．　活动一活动二如图,AB是⊙O的一条弦, 直径CD⊥AB, 垂足为E.
(1)圆是轴对称图形吗? 如果是, 它的对称轴是什么?
(2)你能发现图中有那些相等的线段和弧? 为什么?·OABCDE(1)圆是轴对称图形.直径CD所在的直线是它的对称轴.(2) 线段: AE=BE垂径定理垂直于弦的直径平分弦,并且平分弦所的两条弧.老师提示:
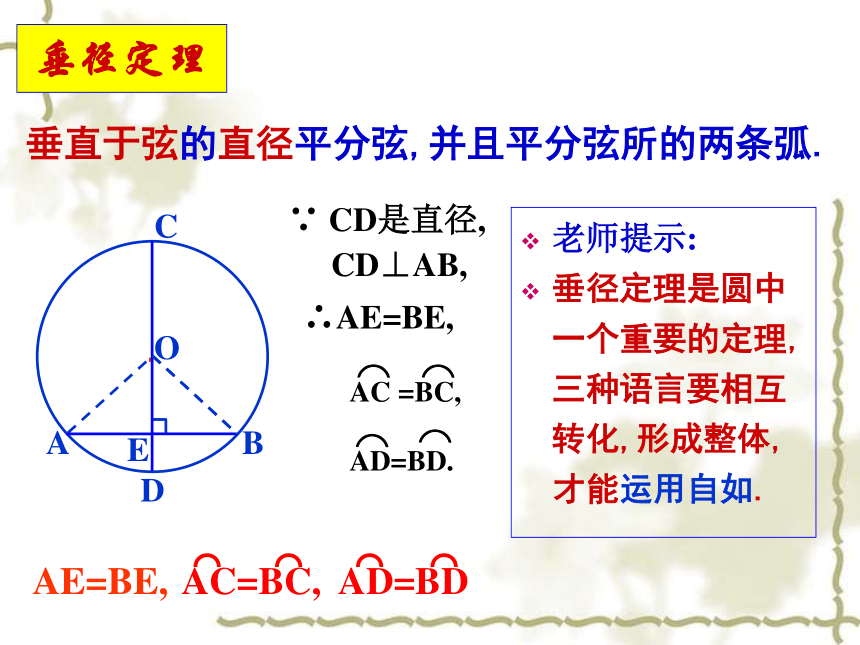
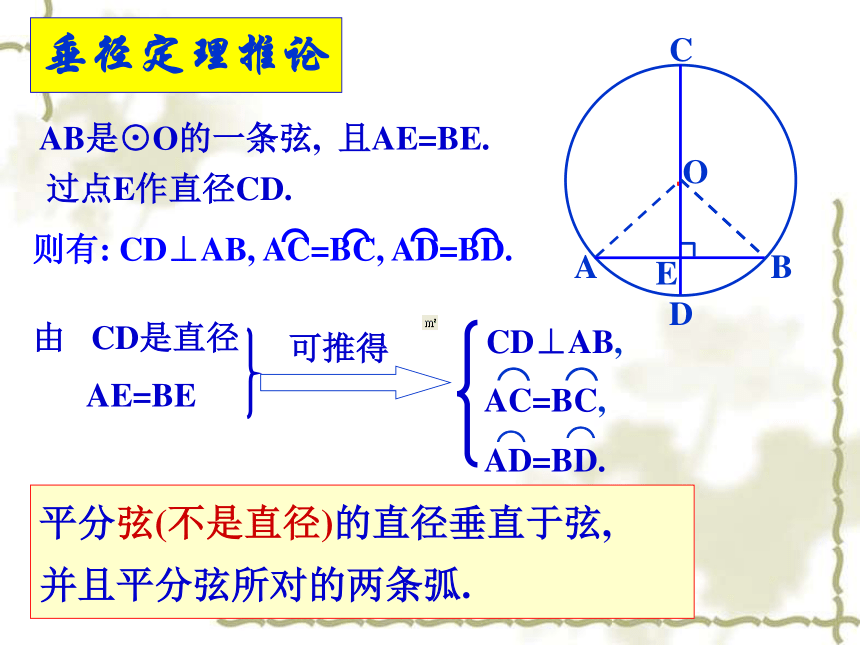
垂径定理是圆中一个重要的定理,三种语言要相互转化,形成整体,才能运用自如.·OABCDEAE=BE,AC=BC, AD=BD⌒⌒⌒⌒CD⊥AB,垂径定理推论AB是⊙O的一条弦, 且AE=BE.过点E作直径CD.由 CD是直径 AE=BE平分弦(不是直径)的直径垂直于弦,
并且平分弦所对的两条弧.·OABCDE则有: CD⊥AB, AC=BC, AD=BD.⌒⌒⌒⌒3.下列说法中，正确的是( )
A、圆的任意一条直径都是它的对称轴
B、经过圆心的直线都是圆的对称轴
C、与圆相交的直线是圆的对称轴
D、与半径垂直的直线是圆的对称轴练习1.圆是 对称图形,它的对称轴是 .2.垂直于弦的直径平分 ,并且平分 .轴直径所在的直线弦弦所对的两条弧B4.下列命题正确的个数是( )
(1)垂直于弦的直线平分这条弦
(2)平分弦的直径垂直于这条弦
(3)菱形的四个顶点在同一个圆上
(4)过圆上一点可以作出圆的最长弦能作无数条
A.1个 B.2个 C.3个 D.以上答案都不对 练习D例1.已知，⊙O中，弦AB的长为8厘米，圆心O到AB的距离是3厘米，
求⊙O的半径.A .OEB解：答：⊙O的半径为5cm.∵OE⊥AB在Rt△AEO中,例2.如图,在⊙O中,AB、AC为互相垂直且相等的两条弦，OD⊥AB于D，OE⊥AC于E，
求证四边形ADOE是正方形．D证明：∴四边形ADOE为矩形，又 ∵AC=AB∴ AE=AD∴ 四边形ADOE为正方形.∵OE⊥AC,OD⊥AB,AB⊥AC∴∠OEA=∠EAD=∠ODA=90°1.已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C，D两点.
则AC和BD有什么大小关系?试说明理由.证明:过O作OE⊥AB于E，
则AE=BE，CE=DE。
∴ AE-CE=BE-DE
即 AC=BD若AB=8厘米，CD=4厘米，求圆环的面积。练习2.已知，⊙O的直径AB和弦CD相交于点E，AE=6厘米，EB=2厘米，∠BED=30°，
求CD的长。说明：
解决有关圆的问题，
常常需要添加辅助线，
针对各种具体情况，辅助线的添加有一定的规律，本例和上例中作“垂直于弦的直径”就是一个很好的例证。练习F1.在直径是20cm的⊙O中，∠AOB的度数是60°, 那么弦AB的弦心距是　　　　　. 圆的圆心到圆上弦的距离叫做弦心距。2.弓形的弦长为6cm，弓形的高为2cm，则这弓形所在的圆的半径为　　　　　　.