人教版五年级上册数学《平行四边形的面积》(课件)-(共32张PPT)
文档属性
| 名称 | 人教版五年级上册数学《平行四边形的面积》(课件)-(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-10 15:00:10 | ||
图片预览







文档简介
(共32张PPT)
人教版义务教育教科书五年级上册
第六单元《多边形面积》
平形四边形的面积
同学们我们学习过哪些平面图形
长方形面积=长×宽
正方形面积=边长×边长
c
z
p
s
t
y
cm
zm
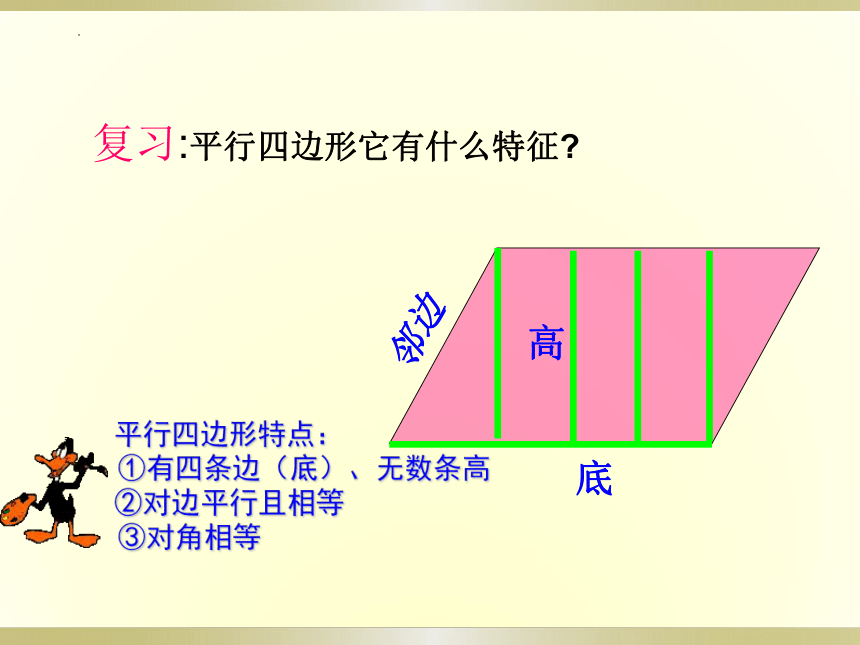
复行四边形它有什么特征
高
底
平行四边形特点:
①有四条边(底)、无数条高
②对边平行且相等
③对角相等
邻边
6米
4米
6米
4米
八戒、沙僧你们俩去把那
两块地的白菜收割回来。
我挑长方形这块,
面积小点,可以少做点
哈哈
老猪,你的如意算盘打错了!
二师兄,你先挑,剩下的给我。
5米
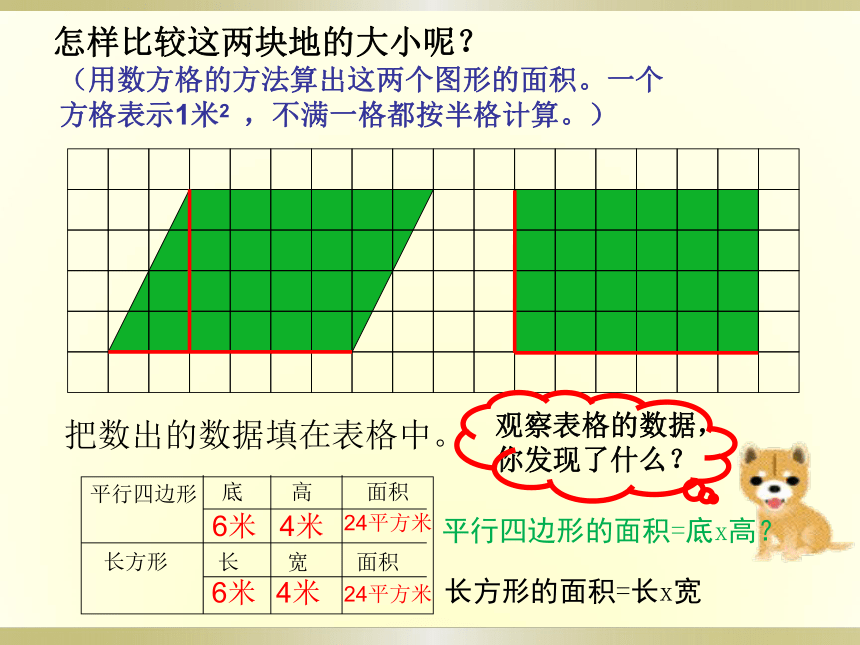
(用数方格的方法算出这两个图形的面积。一个方格表示1米2 ,不满一格都按半格计算。)
把数出的数据填在表格中。
平行四边形
长方形
底 高 面积
长 宽 面积
6米
4米
6米
4米
观察表格的数据,你发现了什么?
24平方米
24平方米
怎样比较这两块地的大小呢?
长方形的面积=长x宽
平行四边形的面积=底x高?
不数方格,我们可以怎样计算平行四边形的面积呢?
能不能把平行四边形变成一个长方形?
先沿高剪开,再通过平移拼成……
一、大胆猜想、动手操作
讨论:平行四边形有无数条高,是不是沿任意一条高剪开,然后通过平移都能得到一个长方形呢?
二、小组合作,深入探究
(1)你是怎样把平行四边形转化成长方形的,
转化后面积大小有没有变化?
(2)转化后的长方形的长与原来平行四边形的
底有什么关系?
(3)转化后的长方形的宽与原来平行四边形的
高有什么关系?
(4)怎么计算平行四边形的面积?
想一想,剪一剪,拼一拼
高
底
高
底
高
底
讨论:
1、转化成的长方形的面积与原来的平行四边形的面积比较,有没有变化?
2、这个长方形的长与平行四边形的底有什么关系?
3、这个长方形的宽与平行四边形的高有什么关系?
4、能否根据长方形的面积公式推导出平行四边形的面积公式?
面积没变
相等
相等
= ×
= ×
平行四边形的面积 = 底×高
三、小组交流,得出结论
底
长
高
宽
想一想:拼成的长方形与原来的平行四边形之间有怎样的关系?
用字母表示:S = ɑh
长方形的面积
平行四边形的面积
长
底
宽
高
例1
沙僧选的的平行四边形菜地的底是6米,高是4米,它的面积是多少?
S=ah=4×6=24(平方米)
答:它的面积是24 平方米。
6米
4米
6m
12m
3m
9m
4m
6m
悟空猴毛一吹变出了三块地,考考八戒哪块地面积最大 。八戒为难了……
你能帮帮他吗?
1、口算下面每个平行四边形的面积:
3厘米
4厘米
5分米
4分米
5米
3米
4米
注意:面积公式当中的底和高必须是相对应的一组。
8×7=56(平方分米)( )
x
2、下面平行四边形面积的计算对吗?
8分米
7分米
6米
3米
6×3=18(平方米)( )
x
3.下面平行四边形面积的计算对吗?
4.计算下图的面积。
比较下列平行四边形的面积,你能发现什么?
高
底
发现:等底等高的平行四边形面积相等。
五、拓展
选择:将正确答案的序号填在括号里。
(1)下面两个平行四边形的面积( )
A、不相等
B、相等
C 、可能相等
B
拓展练习1
选择:将正确答案的序号填在括号里。
(2)如图:
长方形面积( )平行四边形的面积。
A、大于 B、小于 C 、等于
C
拓展练习2
选择:将正确答案的序号填在括号里。
(3)把一个长方形拉成一个平行四边形后,
它的面积( ),周长( )
A、 比原来大 B、 比原来小
C、与原来相等
D、无法确定
B
c
拓展练习3
在方格纸上画出两个不同的平行四边形,使它们的面积
与图中的平行四边形的面积相等。
六、动手画一画
6×2=12
3×4=12
4×3=12
这节课你有什么收获?
我们是如何推导出平行四边形面积计算公式的?
人教版义务教育教科书五年级上册
第六单元《多边形面积》
平形四边形的面积
同学们我们学习过哪些平面图形
长方形面积=长×宽
正方形面积=边长×边长
c
z
p
s
t
y
cm
zm
复行四边形它有什么特征
高
底
平行四边形特点:
①有四条边(底)、无数条高
②对边平行且相等
③对角相等
邻边
6米
4米
6米
4米
八戒、沙僧你们俩去把那
两块地的白菜收割回来。
我挑长方形这块,
面积小点,可以少做点
哈哈
老猪,你的如意算盘打错了!
二师兄,你先挑,剩下的给我。
5米
(用数方格的方法算出这两个图形的面积。一个方格表示1米2 ,不满一格都按半格计算。)
把数出的数据填在表格中。
平行四边形
长方形
底 高 面积
长 宽 面积
6米
4米
6米
4米
观察表格的数据,你发现了什么?
24平方米
24平方米
怎样比较这两块地的大小呢?
长方形的面积=长x宽
平行四边形的面积=底x高?
不数方格,我们可以怎样计算平行四边形的面积呢?
能不能把平行四边形变成一个长方形?
先沿高剪开,再通过平移拼成……
一、大胆猜想、动手操作
讨论:平行四边形有无数条高,是不是沿任意一条高剪开,然后通过平移都能得到一个长方形呢?
二、小组合作,深入探究
(1)你是怎样把平行四边形转化成长方形的,
转化后面积大小有没有变化?
(2)转化后的长方形的长与原来平行四边形的
底有什么关系?
(3)转化后的长方形的宽与原来平行四边形的
高有什么关系?
(4)怎么计算平行四边形的面积?
想一想,剪一剪,拼一拼
高
底
高
底
高
底
讨论:
1、转化成的长方形的面积与原来的平行四边形的面积比较,有没有变化?
2、这个长方形的长与平行四边形的底有什么关系?
3、这个长方形的宽与平行四边形的高有什么关系?
4、能否根据长方形的面积公式推导出平行四边形的面积公式?
面积没变
相等
相等
= ×
= ×
平行四边形的面积 = 底×高
三、小组交流,得出结论
底
长
高
宽
想一想:拼成的长方形与原来的平行四边形之间有怎样的关系?
用字母表示:S = ɑh
长方形的面积
平行四边形的面积
长
底
宽
高
例1
沙僧选的的平行四边形菜地的底是6米,高是4米,它的面积是多少?
S=ah=4×6=24(平方米)
答:它的面积是24 平方米。
6米
4米
6m
12m
3m
9m
4m
6m
悟空猴毛一吹变出了三块地,考考八戒哪块地面积最大 。八戒为难了……
你能帮帮他吗?
1、口算下面每个平行四边形的面积:
3厘米
4厘米
5分米
4分米
5米
3米
4米
注意:面积公式当中的底和高必须是相对应的一组。
8×7=56(平方分米)( )
x
2、下面平行四边形面积的计算对吗?
8分米
7分米
6米
3米
6×3=18(平方米)( )
x
3.下面平行四边形面积的计算对吗?
4.计算下图的面积。
比较下列平行四边形的面积,你能发现什么?
高
底
发现:等底等高的平行四边形面积相等。
五、拓展
选择:将正确答案的序号填在括号里。
(1)下面两个平行四边形的面积( )
A、不相等
B、相等
C 、可能相等
B
拓展练习1
选择:将正确答案的序号填在括号里。
(2)如图:
长方形面积( )平行四边形的面积。
A、大于 B、小于 C 、等于
C
拓展练习2
选择:将正确答案的序号填在括号里。
(3)把一个长方形拉成一个平行四边形后,
它的面积( ),周长( )
A、 比原来大 B、 比原来小
C、与原来相等
D、无法确定
B
c
拓展练习3
在方格纸上画出两个不同的平行四边形,使它们的面积
与图中的平行四边形的面积相等。
六、动手画一画
6×2=12
3×4=12
4×3=12
这节课你有什么收获?
我们是如何推导出平行四边形面积计算公式的?
