双曲线的几何性质
图片预览





文档简介
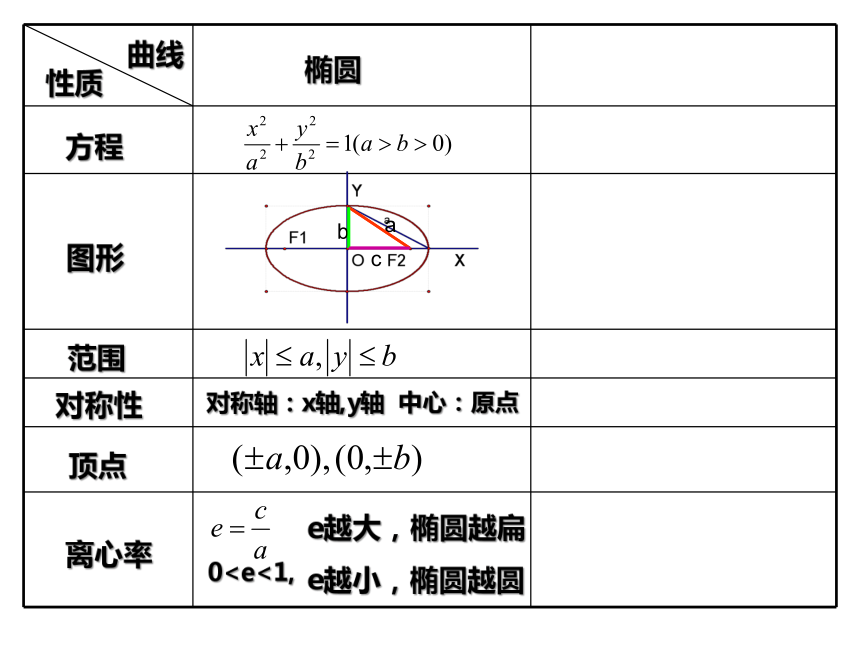
课件24张PPT。 2004年夏季中国在相隔20年后再一次经历了”电荒”的考验,全国的所有大城市都在拉闸限电,我们知道电能是现代生活不可缺少的能源,于是一夜之间全国上下热电厂象竹笋一样拔地而起,而象照片中“粗烟囱”更是随处可见。冷却通风塔如果你是设计师你将如何设计?曲线性质方程范围对称性图形顶点离心率椭圆对称轴:x轴,y轴 中心:原点0e越小,椭圆越圆想一想: 若按照椭圆的几何性质的研究方法来研究双曲线,则双曲线将会具有怎样的几何性质呢?1、范围:2、对称性:3、顶点:4、离心率:试一试:参照椭圆,完成下表曲线性质方程范围对称性图形顶点离心率椭圆对称轴:x,y轴 中心:原点0e越小,椭圆越圆双曲线对称轴:x、y轴 中心:原点双曲线1.gspA1A2为实轴
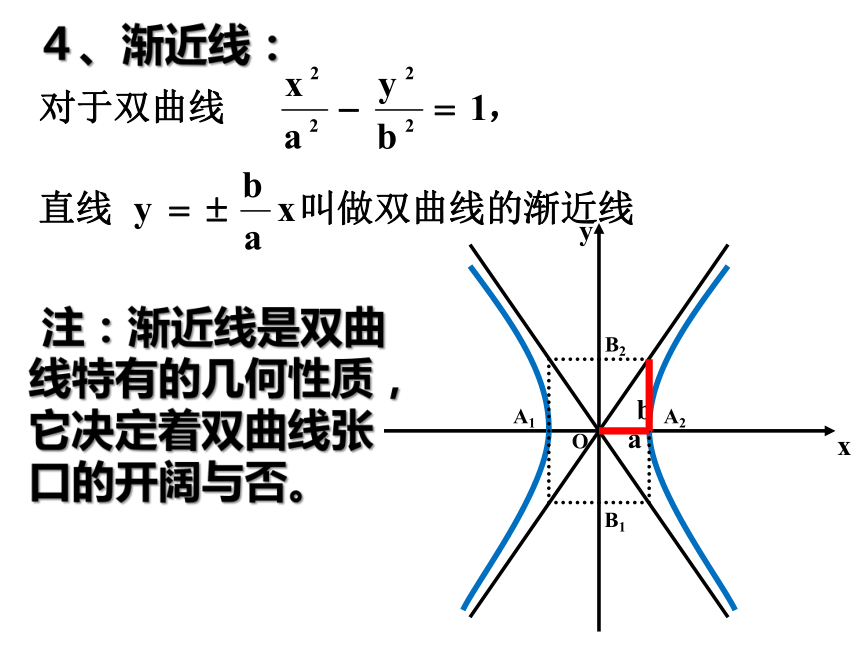
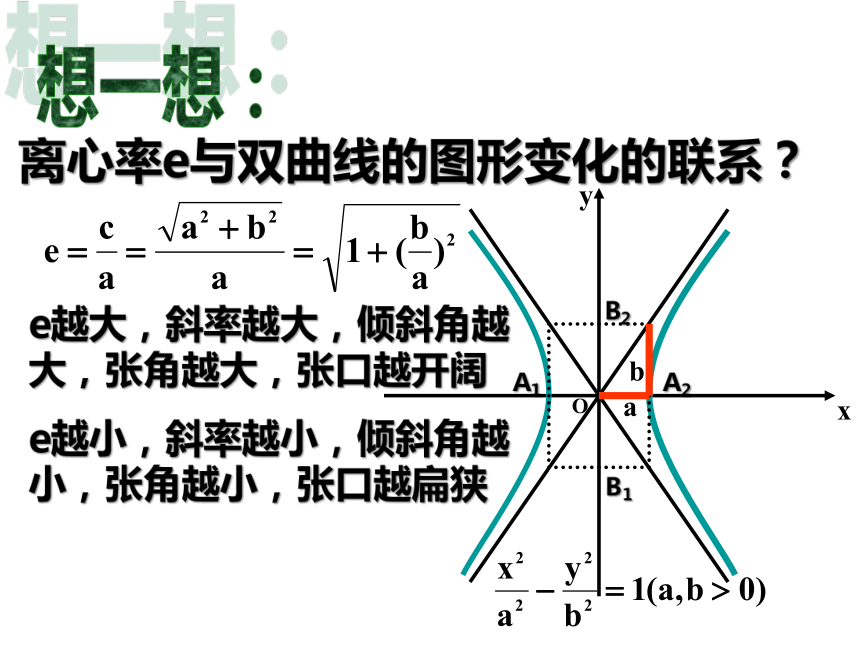
B1B2为虚轴4、渐近线: 注:渐近线是双曲线特有的几何性质,它决定着双曲线张口的开阔与否。思考:那么双曲线的开口大小除用渐近线表示外,还可由什么量决定呢?观察:离心率e与双曲线的图形变化的联系?想一想:e越大,斜率越大,倾斜角越大,张角越大,张口越开阔e越小,斜率越小,倾斜角越小,张角越小,张口越扁狭标准方程图形范围对称性顶点焦点离心率渐近线对称轴x、y轴 中心原点e>1,对称轴:x、y轴 中心:原点e>1,e越大,张口开阔
e越小,张口扁狭e越大,张口开阔
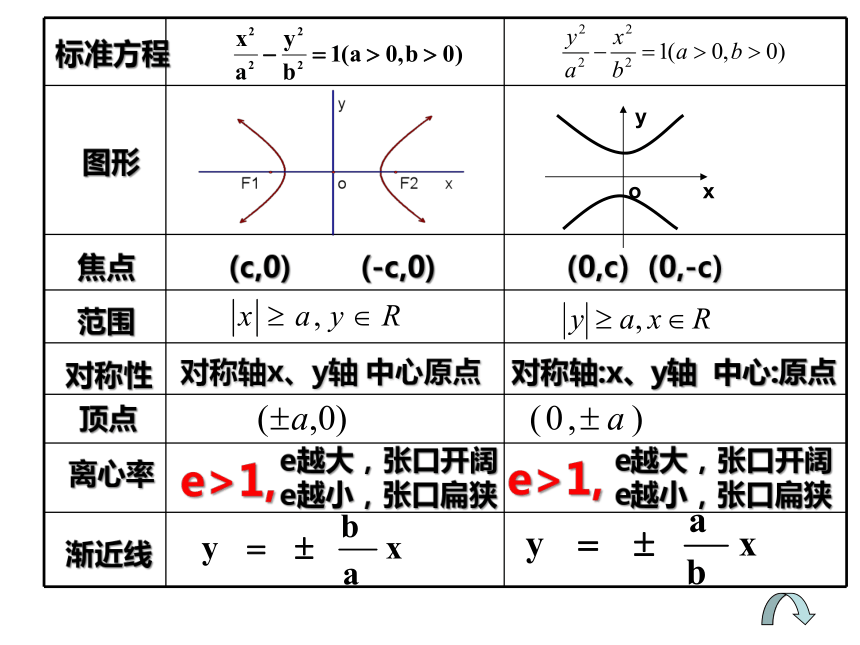
e越小,张口扁狭(c,0) (-c,0)(0,c) (0,-c)应用1:解:双曲线方程可化为:对称轴:x、y轴 中心:原点对称轴:x、y轴 中心:原点(0,5) (0,-5)(5,0) (-5,0)标准方程图形范围对称性顶点焦点离心率渐近线总结:应用2:已知双曲线的虚轴长为6,离心率为2,求双曲线的标准方程。尝试练习:求适合下列条件的双曲线的标准方程:解:总结: 实轴长、虚轴长、离心率、渐近线方程都不能直接确定双曲线的焦点所在的轴,在解决相关问题时应该加以区别:
定性条件与定量条件应用3:解:如图建立直角坐标系xoy,使最小圆的直径x在轴上,圆心与原点重合,则A(12,0)变式1:若上题中的通风塔的上口直径是18米,下口直径是36米,试求通风塔的高度。巩固练习第43页
练习 1、2小结:1、本节课所研究的双曲线的几何性质有哪些?2、需要注意的两个问题:
(1)焦点在不同的轴时的渐近线的方程不同
(2)根据几何性质求双曲线方程时需区分定性与定量条件。课后作业第43页
习题 1⑴⑶、2思考: 仔细分析双曲线方程,还能否发现其图象应在什么样的区域内?观察:由双曲线的对称性知,
只需证明第一象限的部分即可下面我们证明双曲线上的点在沿曲线向远处运动时,与直线逐渐靠拢。
B1B2为虚轴4、渐近线: 注:渐近线是双曲线特有的几何性质,它决定着双曲线张口的开阔与否。思考:那么双曲线的开口大小除用渐近线表示外,还可由什么量决定呢?观察:离心率e与双曲线的图形变化的联系?想一想:e越大,斜率越大,倾斜角越大,张角越大,张口越开阔e越小,斜率越小,倾斜角越小,张角越小,张口越扁狭标准方程图形范围对称性顶点焦点离心率渐近线对称轴x、y轴 中心原点e>1,对称轴:x、y轴 中心:原点e>1,e越大,张口开阔
e越小,张口扁狭e越大,张口开阔
e越小,张口扁狭(c,0) (-c,0)(0,c) (0,-c)应用1:解:双曲线方程可化为:对称轴:x、y轴 中心:原点对称轴:x、y轴 中心:原点(0,5) (0,-5)(5,0) (-5,0)标准方程图形范围对称性顶点焦点离心率渐近线总结:应用2:已知双曲线的虚轴长为6,离心率为2,求双曲线的标准方程。尝试练习:求适合下列条件的双曲线的标准方程:解:总结: 实轴长、虚轴长、离心率、渐近线方程都不能直接确定双曲线的焦点所在的轴,在解决相关问题时应该加以区别:
定性条件与定量条件应用3:解:如图建立直角坐标系xoy,使最小圆的直径x在轴上,圆心与原点重合,则A(12,0)变式1:若上题中的通风塔的上口直径是18米,下口直径是36米,试求通风塔的高度。巩固练习第43页
练习 1、2小结:1、本节课所研究的双曲线的几何性质有哪些?2、需要注意的两个问题:
(1)焦点在不同的轴时的渐近线的方程不同
(2)根据几何性质求双曲线方程时需区分定性与定量条件。课后作业第43页
习题 1⑴⑶、2思考: 仔细分析双曲线方程,还能否发现其图象应在什么样的区域内?观察:由双曲线的对称性知,
只需证明第一象限的部分即可下面我们证明双曲线上的点在沿曲线向远处运动时,与直线逐渐靠拢。
