期末解答题易错专项特训-2023-2024学年数学八年级上册苏教版(含解析)
文档属性
| 名称 | 期末解答题易错专项特训-2023-2024学年数学八年级上册苏教版(含解析) | 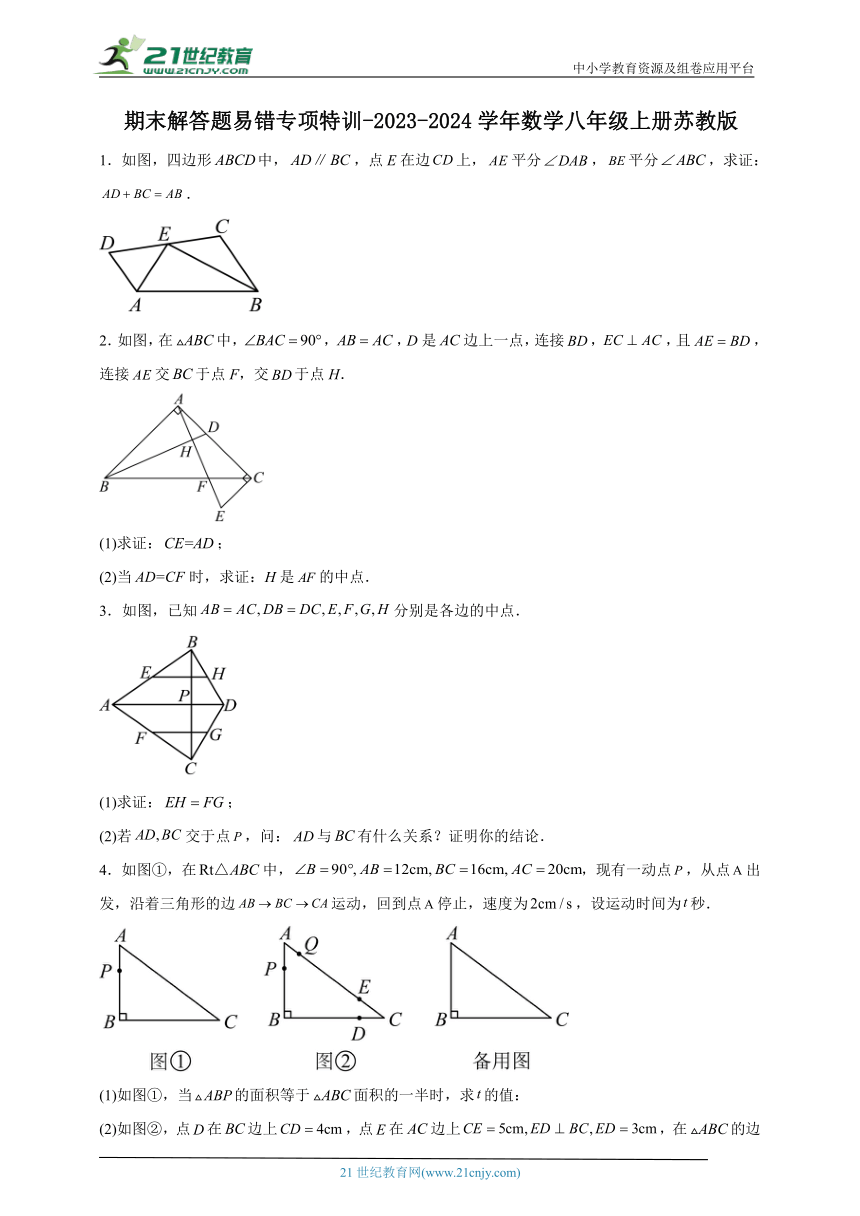 | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-11 17:53:40 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
期末解答题易错专项特训-2023-2024学年数学八年级上册苏教版
1.如图,四边形中,,点E在边上,平分,平分,求证:.
2.如图,在中,,,D是边上一点,连接,,且,连接交于点F,交于点H.
(1)求证:;
(2)当时,求证:H是的中点.
3.如图,已知分别是各边的中点.
(1)求证:;
(2)若交于点,问:与有什么关系?证明你的结论.
4.如图①,在中,,现有一动点,从点出发,沿着三角形的边运动,回到点停止,速度为,设运动时间为秒.
(1)如图①,当的面积等于面积的一半时,求的值:
(2)如图②,点在边上,点在边上,在的边上,若另外有一个动点与点同时从点出发,沿着边运动,回到点停止.在两点运动过程中的某一时刻,以为顶点的三角形恰好与全等,求点的运动速度.
5.如图,在中,,点是上的一点,,交于点,
(1)若,求的度数;
(2)试说明:是等腰三角形.
6.如图,在中,,,的垂直平分线交于点,交于点D,的垂直平分线交于点,交于点.
(1)求的周长;
(2)求的度数;
(3)如果交于点,猜想的形状.
7.如图,点M,N把线段分割成,,,若以,,为边的三角形是一个直角三角形,则称点M,N是线段的勾股分割点.
(1)若点M,N是线段的勾股分割点,,,则的长为__________;
(2)已知M,N把线段分割成,,,若,,,则点M,N是线段的勾股分割点吗?请说明理由,
(3)已知点M,N是线段的勾股分割点,且为直角边,若,,求的长.
8.如图,在四边形中,,,,,,求的度数.
9.如图,在中,,,交于点.动点从点出发,按的路径运动,且速度为,设出发时间为.
(1)求的长;
(2)当秒时,求证:;
(3)当点在边上运动时,若是以为腰的等腰三角形,请你求出所有满足条件的的值.
10.如图是一个滑梯示意图,若将滑梯水平放置,则刚好与一样长,已知滑梯的高度为4米,为1米.
(1)求滑道的长度;
(2)若把滑梯改成滑梯,使,则求出的长.(精确到米,参考数据:)
11.阅读下面的文字,解答后面的问题.
例如:∵,即,∴的整数部分为2,小数部分为.
(1)的整数部分是______,小数部分是______;
(2)如果的小数部分为,的整数部分为,求的值.
12.已知,,满足等式.
(1)求、、的值;
(2)判断以、、为边能否构成三角形?若能构成三角形,此三角形是什么形状的三角形?若不能,请说明理由.
13.如图,在所给的网格图中,完成下列各题.
(1)画出格点关于直线的对称;
(2)若点A的坐标为,点B的坐标为,则的坐标为_________
(3)若相邻两个格点间隔2个单位,求的面积.
14.在平面直角坐标系中,直线l为一、三象限角平分线,点P关于y轴的对称点称为P的一次反射点,记作;关于直线l的对称点称为点P的二次反射点,记作.例如,点的一次反射点为,二次反射点为.根据定义,回答下列问题:
(1)点的一次反射点为__________,二次反射点为__________;
(2)当点A在第三象限时,点,,中可以是点A的二次反射点的是__________;
(3)若点A在第二象限,点,分别是点A的一次、二次反射点,,则射线与x轴所夹锐角的度数是__________;
(4)若点A在y轴左侧,点,分别是点A的一次、二次反射点,是等腰直角三角形,请直接写出点A在平面直角坐标系中的位置.
15.小南在阅读物理课外书时,了解到在弹性限度内,弹簧的长度与所挂物体质量之间满足一次函数关系.他通过实验验证了这个事实,他的测量结果如表所示:
所挂物体质量 0 1 2 3
弹簧的长度 3 4 5 6
(1)根据所测量的数据,求该弹簧的长度与所挂物体质量之间的函数关系式;
(2)小南妈妈在市场买了水果,小南将该水果放在袋中(袋子的质量忽略不计)挂到该弹簧下(在弹性限度内),并测得弹簧的长度为.请你通过计算帮助小南确定该市场老板的称是否足称.
16.某贸易公司销售一批玉米种子,若一次购买量不超过千克.种子价格为元/千克;若一次购买量超过千克,但未超千克,超过千克部分的种子价格打八折;若一次购买量超过千克,前千克照上述规定外,超过千克部分的种子打七折;设买种子费用为(元),购买种子数量为(千克).
(1)若小王购买种子数量为千克,请计算他花的费用应该是多少;
(2)若一次购买量超过千克,但未超千克时,求出费用(元)与购买种子数量(千克)之间的函数关系式;
(3)当一次购买量超过千克时,求出费用(元)与购买种子数量为(千克)之间的函数关系式;
(4)小王在该公司一次性购买这批玉米种子,共花了元,求:小王购买了多少千克种子?
17.为了响应国家提倡的“节能环保”号召,某公司研发出一款新能源纯电动车,如图是这款电动车充满电后,蓄电池剩余电量y(千瓦时)关于已行驶路程x(千米)的函数图象.
(1)当时,千瓦时的电量新能源纯电动车能行驶的路程为千米,则 _____ ;
(2)当时,求y关于x的函数表达式;
(3)请计算当新能源纯电动车已行驶160千米时,蓄电池的剩余电量.
18.某校甲、乙两班参加植树活动.乙班先植树20棵,然后甲班才开始与乙班一起植树.设甲班植树的总量为(棵),乙班植树的总量为(棵),两班一起植树所用的时间(从甲班开始植树时计时)为x(时),分别与x之间的部分函数图象如图所示.
(1)当时,分别求与x之间的函数关系式.
(2)如果甲、乙两班均保持前4个小时的工作效率,通过计算说明,当时,甲、乙两班植树的总量之和能否超过180棵.
参考答案:
1.证明见解析
【分析】在上截取,连接,分别证明,,再根据全等三角形的性质可得结论.
【详解】证明:在上截取,连接,
∵平分,
∴,
在和中,
∴,
∴,
∵,平分,平分,
∴,,
∴,
∴,,
∴,
在和中,
∴,
∴,
∴.
【点睛】本题考查了全等三角形的判定和性质、角平分线的定义和平行线的性质,解决本题的关键是正确的作出辅助线.
2.(1)见解析
(2)见解析
【分析】(1)根据证明即可解决问题;
(2)根据全等三角形的性质和三角形内角和定理求出相应的角度,然后利用等腰三角形三线合一的性质即可解决问题.
【详解】(1)∵,
∴,
在与中,
,
∴,
∴;
(2)由(1)知,,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
由(1)知,,
∴,
∴,
∴,
∴H是的中点.
【点睛】本题考查了全等三角形的判定与性质,等腰直角三角形的性质,三角形内角和定理等知识,熟练掌握全等三角形的判定与性质是解题的关键.
3.(1)见解析
(2)且平分,证明见解析
【分析】(1)证明,得到,证明,,即可证明,得到结论;
(2)证明,则,由得到即可得到,且平分.
【详解】(1)证明:在和中,
∴.
.
.
同理,可证.
在和中,
.
.
(2)解:,且平分,证明如下:
由(1)的证明过程知,
.
在和中,
.
.
.
【点睛】此题考查了全等三角形的判定和性质,根据条件选择合适的全等三角形的判定是解题的关键.
4.(1)或19
(2)或或或
【分析】(1)根据三角形中线平分三角形面积可知,当点P为的中点时和点P为中点时,的面积等于面积的一半,据此根据时间路程速度进行求解即可;
(2)根据题意分四种情况进行分析,利用全等三角形的性质得出点所走的路程,进而可求出的运动时间,即的运动时间,再利用速度路程时间求解即可.
【详解】(1)解:当点P在上时,由三角形中线平分三角形面积可知,当点P为的中点时,的面积等于面积的一半,
∴此时,
同理当点P为中点时,的面积等于面积的一半,
∴此时;
综上所述,t的值为10或19;
(2)解:设点的运动速度为,
由题意得,,
①当点在上,点在上,时,
,
∴,
解得;
②当点在上,点在上,时,
,
∴,
解得;
③当点在上,点在上,时,
,
∴点P的路程为,点Q的路程为
∴,
解得:;
④当点在上,点在上,时,
,
∴点P的路程为,点Q的路程为
∴,
解得:;
综上所述,点的运动速度为或或或.
【点睛】本题主要考查了三角形中线的性质,全等三角形的性质,利用分类讨论的思想求解是解题的关键.
5.(1)
(2)见解析
【分析】本题考查了三角形内角和定理和等腰三角形性质和判定的应用;
(1)推出,根据三角形内角和定理求出,即可求出答案.
(2)根据等腰三角形性质得出,根据平行线性质得出,推出即可.
【详解】(1)解:,
,
,
.
(2)证明:,
,
,
,
.
是等腰三角形.
6.(1)12
(2)
(3)是等腰三角形
【分析】本题考查垂直平分线的性质,等腰三角形的性质,三角形内角和定理:
(1)根据垂直平分线的性质可得,,则;
(2)根据三角形内角和定理求出,根据等边对等角可得,,则;
(3)根据垂直平分线的性质可得.
【详解】(1)解:是的垂直平分线,是的垂直平分线,
,,
,
即的周长为12;
(2)解:,
,
,,
,,
;
(3)解:交于点,
点P在的垂直平分线上,也在的垂直平分线上,
,,
,
是等腰三角形.
7.(1)或
(2)点M,N是线段的勾股分割点,理由见解析
(3)或
【分析】(1)根据题意和勾股定理,分为直角边和为斜边两种情况求解即可;
(2)根据勾股定理的逆定理和题中定义判断即可;
(3)设,根据题意和勾股定理,分为直角边和为斜边两种情况求解即可.
【详解】(1)解:若为直角边时,则;
若为斜边时,则,
故答案为:或;
(2)解:点M,N是线段的勾股分割点,理由为:
∵,,
∴,
∴点M,N是线段的勾股分割点;
(3)解:设,则,
∵点M,N是线段的勾股分割点,
∴若为直角边时,则,
∴,解得,
这时,,符合题意;
若为斜边时,则,
∴,解得,
这时,,符合题意,
综上,的长为或.
【点睛】本题考查勾股定理及其逆定理,理解题中定义,利用分类讨论求解是解答的关键.
8.
【分析】根据勾股定理求得,再利用勾股定理的逆定理得到即可求解.
【详解】解:∵,,
∴,
∵,,
∴,
∴,又,
∴.
【点睛】本题考查勾股定理及其逆定理,利用勾股定理的逆定理得到是解答的关键.
9.(1);
(2)见解析;
(3)满足条件的t的值为或.
【分析】(1)如图1中,作于H.根据即可求出;
(2)证明,可得;
(3)分两种情形①.②分别求解即可.
【详解】(1)解:如图1中,作于H.
∵,
∴,
∴,
∵,
∴;
(2)证明:当时,,此时点P在边上,,
如图2中,
由(1)可知,
∴,
∵,
∴,
∴,
∴;
(3)解:当点P在上时,,
①如图3-1中,当时,
∵,
∴,
∴.
②如图3-2中,当时,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
综上所述,满足条件的t的值为或.
【点睛】本题考查勾股定理,等腰三角形的性质,三角形的面积等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.
10.(1)米
(2)米
【分析】(1)由题意可得:是直角三角形,,且,设滑道的长度为米,则米,米,由勾股定理得出方程,解方程即可;
(2)设米,则米,由勾股定理得(米),则,解得,即可解决问题.
【详解】(1)解:由题意可得:是直角三角形,,且,
,,
,,
设滑道的长度为米,则米,米,
在中,由勾股定理得:,
解得:,
答:滑道的长度为米;
(2),
,
,
设米,则米,
(米),
,
解得:,
(米),
由(1)可知,(米),
(米).
答:的长约为米.
【点睛】本题考查了勾股定理的应用以及含角的直角三角形的性质等知识,熟练掌握勾股定理是解题的关键.
11.(1)4;
(2)1
【分析】(1)先估算的大小,继而即可求得其整数部分与小数部分;
(2)分别估算的大小,进而求得a,b的值,代入代数式进行计算即可求解.
【详解】(1)∵,
∴,
∴的整数部分是4,小数部分是.
故答案为:4,;
(2)∵,
∴,
∴的整数部分是2,小数部分,
∵,
∴,
∴的整数部分.
∴.
【点睛】本题考查了无理数的估算,代数式求值,掌握实数的运算法则是关键.
12.(1)a=,b=5,c=
(2)能,三角形为直角三角形
【分析】(1)根据非负数的性质到,即可得到、、的值;
(2)先利用三角形的三边关系判断能构成三角形,再利用勾股定理的逆定理判断三角形为直角三角形即可.
【详解】(1)解:∵,,
∴,
∴,,.
(2)∵,满足三边关系,
∴a、b、c能构成三角形,
∵,
∴,
∴三角形为直角三角形.
【点睛】此题考查二次根式的非负性、非负数的性质、勾股定理的逆定理、三角形三边关系等知识,熟练掌握勾股定理的逆定理、三角形三边关系是解题的关键.
13.(1)见解析
(2)
(3)10
【分析】(1)根据轴对称的性质作图即可;
(2)由点A的坐标为,点B的坐标为,可知,对称轴为直线,进而可求;
(3)根据,计算求解即可
【详解】(1)解:由轴对称的性质作图如下,即为所求;
(2)解:∵点A的坐标为,点B的坐标为,
∴,对称轴为直线,
∴,
故答案为:;
(3)解:由题意知,,
∴的面积为.
【点睛】本题考查了作轴对称图形,轴对称的性质,坐标与图形等知识.解题的关键在于正确的作图.
14.(1)
(2)
(3)或
(4)点A在x轴的负半轴上或直线上
【分析】(1)根据一次反射点,二次反射点的定义求解;
(2)根据一次反射点,二次反射点的定义判断的位置即可;
(3)判断出射线与轴的夹角,可得结论;
(4)利用图象法,点A在轴负半轴上或直线上满足条件.
【详解】(1)点的一次反射点为,二次反射点为;
故答案为:,;
(2)∵点在第三象限时,
∴一次反射点在第四象限,二次反射点在第二象限,
∴点中可以是点A的二次反射点的是;
故答案为:;
(3)如图1中,
∵,
∴与轴的夹角为或,
根据对称性可知,与轴所夹锐角的度数为或;
(4)如图2中,观察图象可知,当点A在轴上时,是等腰直角三角形.
如图3中,观察图象可知,当点A在直线上时,是等腰直角三角形.
综上所述,点A在轴负半轴上或直线上.
【点睛】本题考查坐标与图形变化——对称,等腰直角三角形的判定和性质,解题的关键是理解一次反射点、二次反射点的定义,学会利用图象法解决问题.
15.(1)
(2)该市场老板的称足称
【分析】本题考查了一次函数的应用,解题的关键是读懂题意,掌握待定系数法求函数解析式.
(1)设与的函数关系式为,用待定系数法求解即可;
(2)将代入(1)中的关系式,求出的值,即可得解.
【详解】(1)解:设弹簧的长度与所挂物体质量之间的函数关系式为,将,代入得:
,解得:,
∴该弹簧的长度与所挂物体质量之间的函数关系式为;
(2)解:将代入得:,
解得,
∵,
∴该市场老板的称足称.
16.(1)元
(2)
(3)
(4)千克
【分析】本题考查列函数关系式及函数的应用,
(1)根据题意,直接计算即可;
(2)根据题意,列出函数关系式,并化简即可;
(3)根据题意,列出函数关系式,并化简即可;
(4)先判断小王购买种子千克数的范围,再代入相应的函数关系式,解出即可;
理解题意,掌握问题中的数量关系是解题的关键.
【详解】(1)解:(元)
∴小王购买种子数量为千克时,他花的费用应该是元;
(2),
∴费用(元)与购买种子数量(千克)之间的函数关系式为;
(3),
∴费用(元)与购买种子数量为(千克)之间的函数关系式:;
(4)∵当时,,
又当购买的种子是千克时,花的费用是:,
∵,
∴小王购买的种子超过千克但没超过千克,
∴,
解得:,
∴小王购买了千克种子.
17.(1)30
(2)
(3)汽车已行驶千米时,蓄电池的剩余电量千瓦时
【分析】本题考查一次函数的应用,解答本题的关键是明题意,利用数形结合的思想解答.
(1)根据函数图象中的数据,1千瓦时的电量新能源纯电动车能行驶的路程为5千米,汽车已经行驶的路程,求出a的值;
(2)根据函数图象中的数据,可以计算出当时,y关于x的函数解析式,
(3)然后将x=160代入求出相应的y值即可.
【详解】(1)由图象可得,
当时,千瓦时的电量新能源纯电动车能行驶的路程为千米,汽车能行驶千米耗电为:(千瓦时),
;
(2)当时,设关于的函数解析式为,
点,在该函数图象上,
,
解得,
即当时,关于的函数解析式是;
(3)当时,,
答:关于的函数解析式是,当汽车已行驶千米时,蓄电池的剩余电量千瓦时.
18.(1)
(2)甲、乙两班植树的总量之和能超过180棵,见解析
【分析】本题主要考查了一次函数与一元一次方程相结合.
(1)通过看图,分析各数据,根据一次函数的性质,列出方程组,求出k、b的值,再列出函数关系式,需注意取值范围;
(2)将数据代入函数关系式即可求出.
【详解】(1)设,
将坐标代入,得
则,
∴,
∴,
当时,,
设,
将和分别代入,
解得,,
∴;
(2)当时,
,
即甲、乙两班植树的总量之和能超过180棵;
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末解答题易错专项特训-2023-2024学年数学八年级上册苏教版
1.如图,四边形中,,点E在边上,平分,平分,求证:.
2.如图,在中,,,D是边上一点,连接,,且,连接交于点F,交于点H.
(1)求证:;
(2)当时,求证:H是的中点.
3.如图,已知分别是各边的中点.
(1)求证:;
(2)若交于点,问:与有什么关系?证明你的结论.
4.如图①,在中,,现有一动点,从点出发,沿着三角形的边运动,回到点停止,速度为,设运动时间为秒.
(1)如图①,当的面积等于面积的一半时,求的值:
(2)如图②,点在边上,点在边上,在的边上,若另外有一个动点与点同时从点出发,沿着边运动,回到点停止.在两点运动过程中的某一时刻,以为顶点的三角形恰好与全等,求点的运动速度.
5.如图,在中,,点是上的一点,,交于点,
(1)若,求的度数;
(2)试说明:是等腰三角形.
6.如图,在中,,,的垂直平分线交于点,交于点D,的垂直平分线交于点,交于点.
(1)求的周长;
(2)求的度数;
(3)如果交于点,猜想的形状.
7.如图,点M,N把线段分割成,,,若以,,为边的三角形是一个直角三角形,则称点M,N是线段的勾股分割点.
(1)若点M,N是线段的勾股分割点,,,则的长为__________;
(2)已知M,N把线段分割成,,,若,,,则点M,N是线段的勾股分割点吗?请说明理由,
(3)已知点M,N是线段的勾股分割点,且为直角边,若,,求的长.
8.如图,在四边形中,,,,,,求的度数.
9.如图,在中,,,交于点.动点从点出发,按的路径运动,且速度为,设出发时间为.
(1)求的长;
(2)当秒时,求证:;
(3)当点在边上运动时,若是以为腰的等腰三角形,请你求出所有满足条件的的值.
10.如图是一个滑梯示意图,若将滑梯水平放置,则刚好与一样长,已知滑梯的高度为4米,为1米.
(1)求滑道的长度;
(2)若把滑梯改成滑梯,使,则求出的长.(精确到米,参考数据:)
11.阅读下面的文字,解答后面的问题.
例如:∵,即,∴的整数部分为2,小数部分为.
(1)的整数部分是______,小数部分是______;
(2)如果的小数部分为,的整数部分为,求的值.
12.已知,,满足等式.
(1)求、、的值;
(2)判断以、、为边能否构成三角形?若能构成三角形,此三角形是什么形状的三角形?若不能,请说明理由.
13.如图,在所给的网格图中,完成下列各题.
(1)画出格点关于直线的对称;
(2)若点A的坐标为,点B的坐标为,则的坐标为_________
(3)若相邻两个格点间隔2个单位,求的面积.
14.在平面直角坐标系中,直线l为一、三象限角平分线,点P关于y轴的对称点称为P的一次反射点,记作;关于直线l的对称点称为点P的二次反射点,记作.例如,点的一次反射点为,二次反射点为.根据定义,回答下列问题:
(1)点的一次反射点为__________,二次反射点为__________;
(2)当点A在第三象限时,点,,中可以是点A的二次反射点的是__________;
(3)若点A在第二象限,点,分别是点A的一次、二次反射点,,则射线与x轴所夹锐角的度数是__________;
(4)若点A在y轴左侧,点,分别是点A的一次、二次反射点,是等腰直角三角形,请直接写出点A在平面直角坐标系中的位置.
15.小南在阅读物理课外书时,了解到在弹性限度内,弹簧的长度与所挂物体质量之间满足一次函数关系.他通过实验验证了这个事实,他的测量结果如表所示:
所挂物体质量 0 1 2 3
弹簧的长度 3 4 5 6
(1)根据所测量的数据,求该弹簧的长度与所挂物体质量之间的函数关系式;
(2)小南妈妈在市场买了水果,小南将该水果放在袋中(袋子的质量忽略不计)挂到该弹簧下(在弹性限度内),并测得弹簧的长度为.请你通过计算帮助小南确定该市场老板的称是否足称.
16.某贸易公司销售一批玉米种子,若一次购买量不超过千克.种子价格为元/千克;若一次购买量超过千克,但未超千克,超过千克部分的种子价格打八折;若一次购买量超过千克,前千克照上述规定外,超过千克部分的种子打七折;设买种子费用为(元),购买种子数量为(千克).
(1)若小王购买种子数量为千克,请计算他花的费用应该是多少;
(2)若一次购买量超过千克,但未超千克时,求出费用(元)与购买种子数量(千克)之间的函数关系式;
(3)当一次购买量超过千克时,求出费用(元)与购买种子数量为(千克)之间的函数关系式;
(4)小王在该公司一次性购买这批玉米种子,共花了元,求:小王购买了多少千克种子?
17.为了响应国家提倡的“节能环保”号召,某公司研发出一款新能源纯电动车,如图是这款电动车充满电后,蓄电池剩余电量y(千瓦时)关于已行驶路程x(千米)的函数图象.
(1)当时,千瓦时的电量新能源纯电动车能行驶的路程为千米,则 _____ ;
(2)当时,求y关于x的函数表达式;
(3)请计算当新能源纯电动车已行驶160千米时,蓄电池的剩余电量.
18.某校甲、乙两班参加植树活动.乙班先植树20棵,然后甲班才开始与乙班一起植树.设甲班植树的总量为(棵),乙班植树的总量为(棵),两班一起植树所用的时间(从甲班开始植树时计时)为x(时),分别与x之间的部分函数图象如图所示.
(1)当时,分别求与x之间的函数关系式.
(2)如果甲、乙两班均保持前4个小时的工作效率,通过计算说明,当时,甲、乙两班植树的总量之和能否超过180棵.
参考答案:
1.证明见解析
【分析】在上截取,连接,分别证明,,再根据全等三角形的性质可得结论.
【详解】证明:在上截取,连接,
∵平分,
∴,
在和中,
∴,
∴,
∵,平分,平分,
∴,,
∴,
∴,,
∴,
在和中,
∴,
∴,
∴.
【点睛】本题考查了全等三角形的判定和性质、角平分线的定义和平行线的性质,解决本题的关键是正确的作出辅助线.
2.(1)见解析
(2)见解析
【分析】(1)根据证明即可解决问题;
(2)根据全等三角形的性质和三角形内角和定理求出相应的角度,然后利用等腰三角形三线合一的性质即可解决问题.
【详解】(1)∵,
∴,
在与中,
,
∴,
∴;
(2)由(1)知,,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
由(1)知,,
∴,
∴,
∴,
∴H是的中点.
【点睛】本题考查了全等三角形的判定与性质,等腰直角三角形的性质,三角形内角和定理等知识,熟练掌握全等三角形的判定与性质是解题的关键.
3.(1)见解析
(2)且平分,证明见解析
【分析】(1)证明,得到,证明,,即可证明,得到结论;
(2)证明,则,由得到即可得到,且平分.
【详解】(1)证明:在和中,
∴.
.
.
同理,可证.
在和中,
.
.
(2)解:,且平分,证明如下:
由(1)的证明过程知,
.
在和中,
.
.
.
【点睛】此题考查了全等三角形的判定和性质,根据条件选择合适的全等三角形的判定是解题的关键.
4.(1)或19
(2)或或或
【分析】(1)根据三角形中线平分三角形面积可知,当点P为的中点时和点P为中点时,的面积等于面积的一半,据此根据时间路程速度进行求解即可;
(2)根据题意分四种情况进行分析,利用全等三角形的性质得出点所走的路程,进而可求出的运动时间,即的运动时间,再利用速度路程时间求解即可.
【详解】(1)解:当点P在上时,由三角形中线平分三角形面积可知,当点P为的中点时,的面积等于面积的一半,
∴此时,
同理当点P为中点时,的面积等于面积的一半,
∴此时;
综上所述,t的值为10或19;
(2)解:设点的运动速度为,
由题意得,,
①当点在上,点在上,时,
,
∴,
解得;
②当点在上,点在上,时,
,
∴,
解得;
③当点在上,点在上,时,
,
∴点P的路程为,点Q的路程为
∴,
解得:;
④当点在上,点在上,时,
,
∴点P的路程为,点Q的路程为
∴,
解得:;
综上所述,点的运动速度为或或或.
【点睛】本题主要考查了三角形中线的性质,全等三角形的性质,利用分类讨论的思想求解是解题的关键.
5.(1)
(2)见解析
【分析】本题考查了三角形内角和定理和等腰三角形性质和判定的应用;
(1)推出,根据三角形内角和定理求出,即可求出答案.
(2)根据等腰三角形性质得出,根据平行线性质得出,推出即可.
【详解】(1)解:,
,
,
.
(2)证明:,
,
,
,
.
是等腰三角形.
6.(1)12
(2)
(3)是等腰三角形
【分析】本题考查垂直平分线的性质,等腰三角形的性质,三角形内角和定理:
(1)根据垂直平分线的性质可得,,则;
(2)根据三角形内角和定理求出,根据等边对等角可得,,则;
(3)根据垂直平分线的性质可得.
【详解】(1)解:是的垂直平分线,是的垂直平分线,
,,
,
即的周长为12;
(2)解:,
,
,,
,,
;
(3)解:交于点,
点P在的垂直平分线上,也在的垂直平分线上,
,,
,
是等腰三角形.
7.(1)或
(2)点M,N是线段的勾股分割点,理由见解析
(3)或
【分析】(1)根据题意和勾股定理,分为直角边和为斜边两种情况求解即可;
(2)根据勾股定理的逆定理和题中定义判断即可;
(3)设,根据题意和勾股定理,分为直角边和为斜边两种情况求解即可.
【详解】(1)解:若为直角边时,则;
若为斜边时,则,
故答案为:或;
(2)解:点M,N是线段的勾股分割点,理由为:
∵,,
∴,
∴点M,N是线段的勾股分割点;
(3)解:设,则,
∵点M,N是线段的勾股分割点,
∴若为直角边时,则,
∴,解得,
这时,,符合题意;
若为斜边时,则,
∴,解得,
这时,,符合题意,
综上,的长为或.
【点睛】本题考查勾股定理及其逆定理,理解题中定义,利用分类讨论求解是解答的关键.
8.
【分析】根据勾股定理求得,再利用勾股定理的逆定理得到即可求解.
【详解】解:∵,,
∴,
∵,,
∴,
∴,又,
∴.
【点睛】本题考查勾股定理及其逆定理,利用勾股定理的逆定理得到是解答的关键.
9.(1);
(2)见解析;
(3)满足条件的t的值为或.
【分析】(1)如图1中,作于H.根据即可求出;
(2)证明,可得;
(3)分两种情形①.②分别求解即可.
【详解】(1)解:如图1中,作于H.
∵,
∴,
∴,
∵,
∴;
(2)证明:当时,,此时点P在边上,,
如图2中,
由(1)可知,
∴,
∵,
∴,
∴,
∴;
(3)解:当点P在上时,,
①如图3-1中,当时,
∵,
∴,
∴.
②如图3-2中,当时,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
综上所述,满足条件的t的值为或.
【点睛】本题考查勾股定理,等腰三角形的性质,三角形的面积等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.
10.(1)米
(2)米
【分析】(1)由题意可得:是直角三角形,,且,设滑道的长度为米,则米,米,由勾股定理得出方程,解方程即可;
(2)设米,则米,由勾股定理得(米),则,解得,即可解决问题.
【详解】(1)解:由题意可得:是直角三角形,,且,
,,
,,
设滑道的长度为米,则米,米,
在中,由勾股定理得:,
解得:,
答:滑道的长度为米;
(2),
,
,
设米,则米,
(米),
,
解得:,
(米),
由(1)可知,(米),
(米).
答:的长约为米.
【点睛】本题考查了勾股定理的应用以及含角的直角三角形的性质等知识,熟练掌握勾股定理是解题的关键.
11.(1)4;
(2)1
【分析】(1)先估算的大小,继而即可求得其整数部分与小数部分;
(2)分别估算的大小,进而求得a,b的值,代入代数式进行计算即可求解.
【详解】(1)∵,
∴,
∴的整数部分是4,小数部分是.
故答案为:4,;
(2)∵,
∴,
∴的整数部分是2,小数部分,
∵,
∴,
∴的整数部分.
∴.
【点睛】本题考查了无理数的估算,代数式求值,掌握实数的运算法则是关键.
12.(1)a=,b=5,c=
(2)能,三角形为直角三角形
【分析】(1)根据非负数的性质到,即可得到、、的值;
(2)先利用三角形的三边关系判断能构成三角形,再利用勾股定理的逆定理判断三角形为直角三角形即可.
【详解】(1)解:∵,,
∴,
∴,,.
(2)∵,满足三边关系,
∴a、b、c能构成三角形,
∵,
∴,
∴三角形为直角三角形.
【点睛】此题考查二次根式的非负性、非负数的性质、勾股定理的逆定理、三角形三边关系等知识,熟练掌握勾股定理的逆定理、三角形三边关系是解题的关键.
13.(1)见解析
(2)
(3)10
【分析】(1)根据轴对称的性质作图即可;
(2)由点A的坐标为,点B的坐标为,可知,对称轴为直线,进而可求;
(3)根据,计算求解即可
【详解】(1)解:由轴对称的性质作图如下,即为所求;
(2)解:∵点A的坐标为,点B的坐标为,
∴,对称轴为直线,
∴,
故答案为:;
(3)解:由题意知,,
∴的面积为.
【点睛】本题考查了作轴对称图形,轴对称的性质,坐标与图形等知识.解题的关键在于正确的作图.
14.(1)
(2)
(3)或
(4)点A在x轴的负半轴上或直线上
【分析】(1)根据一次反射点,二次反射点的定义求解;
(2)根据一次反射点,二次反射点的定义判断的位置即可;
(3)判断出射线与轴的夹角,可得结论;
(4)利用图象法,点A在轴负半轴上或直线上满足条件.
【详解】(1)点的一次反射点为,二次反射点为;
故答案为:,;
(2)∵点在第三象限时,
∴一次反射点在第四象限,二次反射点在第二象限,
∴点中可以是点A的二次反射点的是;
故答案为:;
(3)如图1中,
∵,
∴与轴的夹角为或,
根据对称性可知,与轴所夹锐角的度数为或;
(4)如图2中,观察图象可知,当点A在轴上时,是等腰直角三角形.
如图3中,观察图象可知,当点A在直线上时,是等腰直角三角形.
综上所述,点A在轴负半轴上或直线上.
【点睛】本题考查坐标与图形变化——对称,等腰直角三角形的判定和性质,解题的关键是理解一次反射点、二次反射点的定义,学会利用图象法解决问题.
15.(1)
(2)该市场老板的称足称
【分析】本题考查了一次函数的应用,解题的关键是读懂题意,掌握待定系数法求函数解析式.
(1)设与的函数关系式为,用待定系数法求解即可;
(2)将代入(1)中的关系式,求出的值,即可得解.
【详解】(1)解:设弹簧的长度与所挂物体质量之间的函数关系式为,将,代入得:
,解得:,
∴该弹簧的长度与所挂物体质量之间的函数关系式为;
(2)解:将代入得:,
解得,
∵,
∴该市场老板的称足称.
16.(1)元
(2)
(3)
(4)千克
【分析】本题考查列函数关系式及函数的应用,
(1)根据题意,直接计算即可;
(2)根据题意,列出函数关系式,并化简即可;
(3)根据题意,列出函数关系式,并化简即可;
(4)先判断小王购买种子千克数的范围,再代入相应的函数关系式,解出即可;
理解题意,掌握问题中的数量关系是解题的关键.
【详解】(1)解:(元)
∴小王购买种子数量为千克时,他花的费用应该是元;
(2),
∴费用(元)与购买种子数量(千克)之间的函数关系式为;
(3),
∴费用(元)与购买种子数量为(千克)之间的函数关系式:;
(4)∵当时,,
又当购买的种子是千克时,花的费用是:,
∵,
∴小王购买的种子超过千克但没超过千克,
∴,
解得:,
∴小王购买了千克种子.
17.(1)30
(2)
(3)汽车已行驶千米时,蓄电池的剩余电量千瓦时
【分析】本题考查一次函数的应用,解答本题的关键是明题意,利用数形结合的思想解答.
(1)根据函数图象中的数据,1千瓦时的电量新能源纯电动车能行驶的路程为5千米,汽车已经行驶的路程,求出a的值;
(2)根据函数图象中的数据,可以计算出当时,y关于x的函数解析式,
(3)然后将x=160代入求出相应的y值即可.
【详解】(1)由图象可得,
当时,千瓦时的电量新能源纯电动车能行驶的路程为千米,汽车能行驶千米耗电为:(千瓦时),
;
(2)当时,设关于的函数解析式为,
点,在该函数图象上,
,
解得,
即当时,关于的函数解析式是;
(3)当时,,
答:关于的函数解析式是,当汽车已行驶千米时,蓄电池的剩余电量千瓦时.
18.(1)
(2)甲、乙两班植树的总量之和能超过180棵,见解析
【分析】本题主要考查了一次函数与一元一次方程相结合.
(1)通过看图,分析各数据,根据一次函数的性质,列出方程组,求出k、b的值,再列出函数关系式,需注意取值范围;
(2)将数据代入函数关系式即可求出.
【详解】(1)设,
将坐标代入,得
则,
∴,
∴,
当时,,
设,
将和分别代入,
解得,,
∴;
(2)当时,
,
即甲、乙两班植树的总量之和能超过180棵;
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
