期末解答题易错专项特训-2023-2024学年数学九年级上册苏教版(含解析)
文档属性
| 名称 | 期末解答题易错专项特训-2023-2024学年数学九年级上册苏教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-11 18:00:59 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末解答题易错专项特训-2023-2024学年数学九年级上册苏教版
1.某商店准备销售一种多功能旅行背包,计划从厂家以每个30元的价格进货,经过市场调查发现当每个背包的售价为40元时,月均销量为280个,售价每增长2元,月均销量就相应减少20个.
(1)若使这种背包的月均销量不低于130个,每个背包售价应不高于多少元;
(2)在(1)的条件下,当这种背包销售单价为多少元时,销售利润是3120元?
(3)这种背包的销售利润有可能达到3700元吗?若能,请求出此时的销售单价;若不能,请说明理由.
2.为了喜迎杭州第十九届亚运会,某学校计划对一块宽为,长为的矩形荒地进行改造,要求修筑同样宽鹅卵石小路,余下的部分种上草坪(阴影部分),并使草坪的面积为.现在邀请全校同学参与设计,下面是三位同学分别设计的方案,请你选择一种方案,求出道路的宽为多少米?(根据需要精确到0.1米)
3.已知关于的一元二次方程(为常数).
(1)求证:不论为何值时,方程总有两个不相等的实数根.
(2)设是方程的两个根,且,求的值.
4.阅读下列材料:
利用完全平方公式,将多项式变形为的形式,
例如:.
根据以上材料,解答下列问题:
(1)填空:将多项式变形为的形式,并判断与0的大小关系,
;
所以 0(填“”、“”、“”;
(2)将多项式变形为的形式,并求出多项式的最小值;
(3)求证:、取任何实数时,多项式的值总为正数.
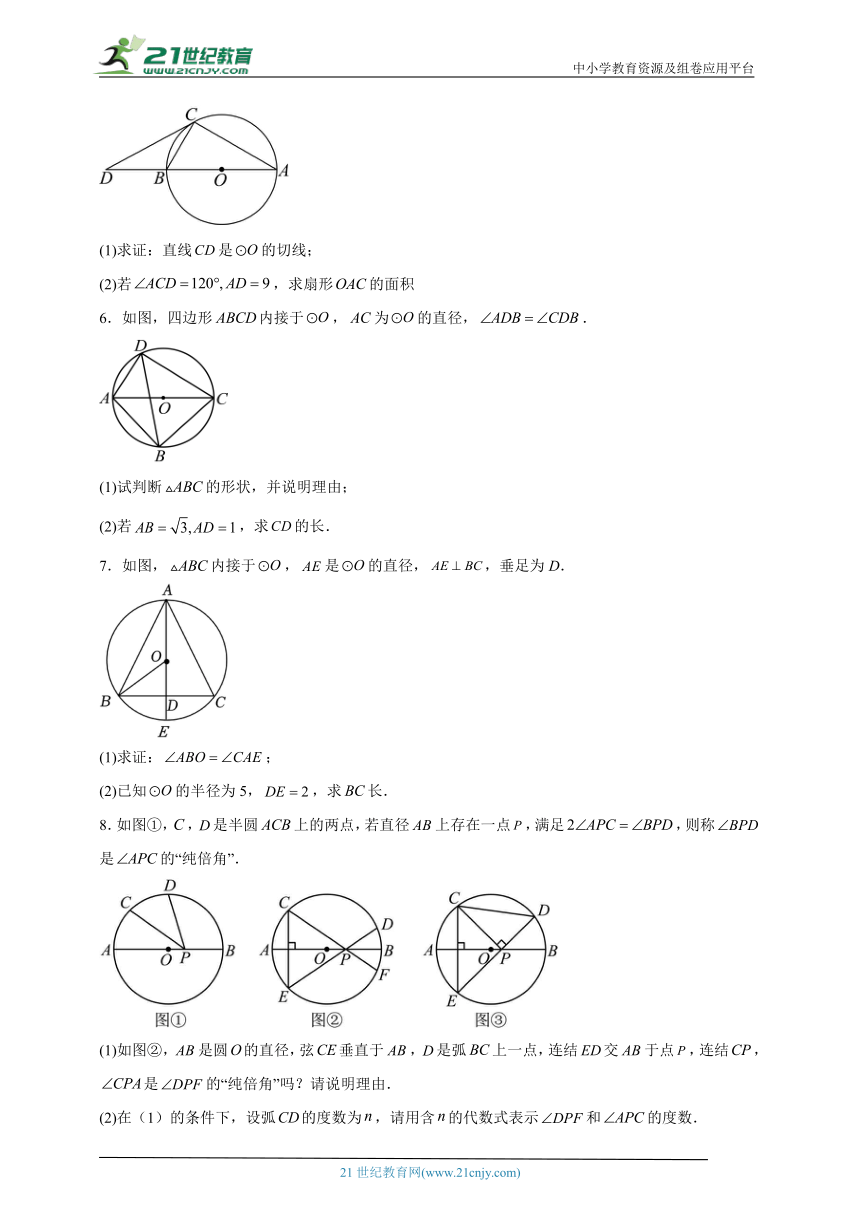
5.如图,在中,是直径,点是圆上一点,在的延长线上取一点,连接,使.求:
(1)求证:直线是的切线;
(2)若,求扇形的面积
6.如图,四边形内接于,为的直径,.
(1)试判断的形状,并说明理由;
(2)若,求的长.
7.如图,内接于,是的直径,,垂足为D.
(1)求证:;
(2)已知的半径为5,,求长.
8.如图①,,是半圆上的两点,若直径上存在一点,满足,则称是的“纯倍角”.
(1)如图②,是圆的直径,弦垂直于,是弧上一点,连结交于点,连结,是的“纯倍角”吗?请说明理由.
(2)在(1)的条件下,设弧的度数为,请用含的代数式表示和的度数.
(3)如图③,在(1)的条件下,连结,直径,.求弦的长.
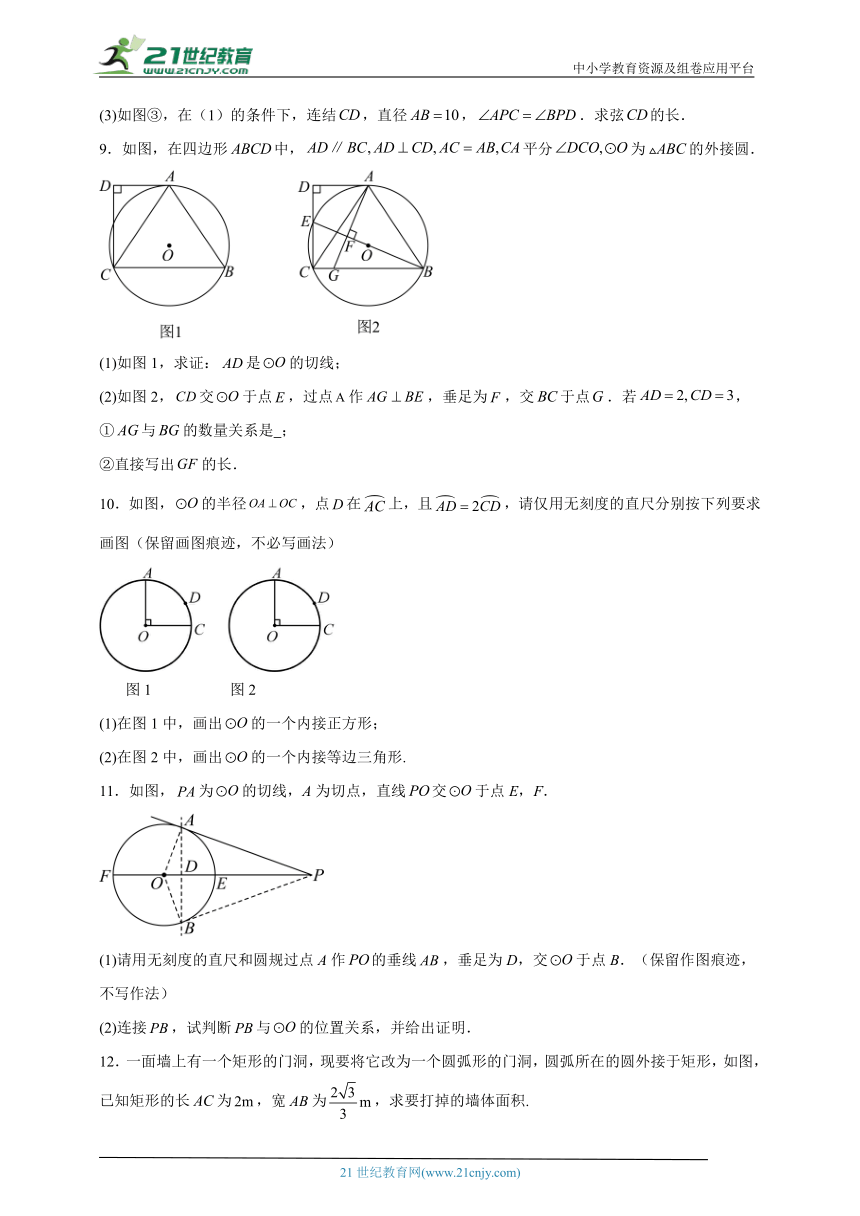
9.如图,在四边形中,平分为的外接圆.
(1)如图1,求证:是的切线;
(2)如图2,交于点,过点作,垂足为,交于点.若,
①与的数量关系是 ;
②直接写出的长.
10.如图,的半径,点在上,且,请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹,不必写画法)
图1 图2
(1)在图1中,画出的一个内接正方形;
(2)在图2中,画出的一个内接等边三角形.
11.如图,为的切线,A为切点,直线交于点E,F.
(1)请用无刻度的直尺和圆规过点A作的垂线,垂足为D,交于点B.(保留作图痕迹,不写作法)
(2)连接,试判断与的位置关系,并给出证明.
12.一面墙上有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,如图,已知矩形的长为,宽为,求要打掉的墙体面积.
13.某地经过多年的环境治理,已将荒山改造成了绿水青山.为估计一林区某种树木的总材积量,随机选取了10棵这种树木,测量每棵树的根部横截面积(单位:)和材积量(单位:),得到如下数据:
样本号 1 2 3 4 5 6 7 8 9 10
根部横截面积x 0.04 0.06 0.04 0.08 0.08 0.05 0.05 0.07 0.07 0.06
材积量y 0.25 0.40 0.22 0.54 0.51 0.34 0.36 0.46 0.42 0.40
(1)估计该林区一颗这种树木平均根部横截面积与平均材积量.
(2)现测量了该林区部分这种树木的根部横截面积,经过测算得到这种树木的根部横截面积总和为.已知树木的材积量与其根部横截面积近似成正比.利用以上数据估计该林区这种树木的总材积量.
14.某中学的国旗护卫队需从甲、乙两队中选择一队身高比较整齐的队员担任护旗手,两队每个队员的身高(单位:cm)如下:
甲队 177 179 178 179 177 178 178 179 178 177
平均数 中位数 众数 方差
甲队 178 a 178 c
乙队 177.1 177 b 0.89
两组样本数据的平均数,中位数,众数,方差如表中数据所示:
(1)表中________,________.
(2)请计算甲队的方差c,并判断哪队队员身高更整齐.
15.陕西历史悠久,是中华文明的重要发祥地之一,有着众多的名胜古迹,其中华山、秦始皇陵和大雁塔等文明古迹堪称为国之瑰宝,吸引着国内外的游客来陕游玩.小明收集了华山、秦始皇陵、大雁塔这三个景点的图片各一张,这些图片大小、形状及背面完全相同,把这三张图片洗匀后背面朝上放置在桌面上(三张图片依次用A,B,C表示).
(1)小明随机抽取一张图片,则抽取到华山图片的概率是______;
(2)小明随机抽取一张图片后,放回洗匀,小华再随机抽取一张图片,请用列表或画树状图的方法求他们都抽取到大雁塔图片的概率.
16.某市今年中考体育测试,其中男生测试项目有1000米跑、立定跳远、掷实心球、一分钟跳绳、引体向上五个项目.考生须从这五个项目中选取三个项目,要求:1000米跑必选,立定跳远和掷实心球二选一,一分钟跳绳和引体向上二选一.
(1)写出男生在体育测试中所有可能选择的结果;
(2)请你用列表法或画树状图法,求出两名男生在体育测试中所选项目完全相同的概率.
参考答案:
1.(1)元
(2)元
(3)不能,理由见解析
【分析】本题考查了一元一次不等式的应用,一元二次方程的应用,一元二次方程根的判别式,根据题意正确的列等式、不等式是解题的关键
(1)设每个背包的售价为元,则月均销量为个,依题意,得:,计算求解即可;
(2)依题意,得:,计算求出满足要求的解即可;
(3)依题意,得:,整理,得:,由,可知该方程无解,然后作答即可.
【详解】(1)解:设每个背包的售价为元,则月均销量为个,
依题意,得:,
解得:,
答:每个背包售价应不高于元.
(2)解:依题意,得:,
整理,得:,
解得:,不合题意,舍去.
答:当这种背包销售单价为元时,销售利润是元.
(3)解:不能,理由如下:
依题意,得:,
整理,得:,
∴,
该方程无解,
答:这种背包的销售利润不可能达到元.
2.道路的宽为1米或道路的宽为2米或道路的宽为米.
【分析】此题主要考查一元二次方程的应用,利用平移把道路进行平移,再根据草地的面积公式列出一元二次方程即可求解,解题的关键是根据题意找到等量关系列出方程进行求解.
【详解】解:选择方案一
设道路的宽为米,根据题意可列方程:
,
整理得:,
解得:,(舍去),
答:道路的宽为1米;
选择方案二
设道路的宽为米,根据题意可列方程:
,
整理得:,
解得:,(舍去),
答:道路的宽为2米;
选择方案三
设道路的宽为米,根据题意可列方程:
,
整理得:,
解得:,(舍去);
答:道路的宽为米.
3.(1)详细见解析.
(2).
【分析】求出判别式的符号,进行判断即可.
利用一元二次方程的解的定义和根与系数的关系求解.
【详解】(1)
方程总有两个不相等的实数根.
(2)是方程的两个根
在中,
即:
解得:或
【点睛】本题考查根的判别式、根与系数的关系以及因式分解等,熟练掌握相关知识点是解题的关键.
4.(1)1;2;
(2)最小值为
(3)证明见解析
【分析】本题考查了配方法的应用,熟练掌握配方法是解题的关键;
(1)模仿题干的例题配方即可,利用平方的非负性与0比较大小;
(2)将多项式配方,根据平方的非负性求出多项式的最小值;
(3)对多项式进行配方即可证明多项式的值总为正数.
【详解】(1)解:
,
,
,
,
故答案为:1;2;;
(2)解:
,
,
当时,有最小值,最小值为;
(3)证明:
,
,,
,
、取任何实数时,多项式的值总为正数.
5.(1)见解析
(2)
【分析】(1)连接,得到,圆周角定理得到,得到,进而得到,即可;
(2)根据,得到,进而得到,进而得到,根据含30度角的直角三角形的性质,得到,求出半径的长,根据扇形的面积公式进行求解即可.
【详解】(1)证明:连接,则:,
∴,
∵是直径,
∴,
∴,
∵,
∴,即:,
∴,
∵是的半径,
∴直线是的切线;
(2)∵,,
∴,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∴扇形的面积为.
【点睛】本题考查切线的判定和性质,圆周角定理,扇形的面积,等边对等角,含30度角的直角三角形.熟练掌握相关知识点,灵活运用,是解题的关键.
6.(1)等腰直角三角形,理由见解析;
(2)
【分析】(1)根据同弧所对的圆周角相等,得到,,进而得到,再根据直径所对的圆周角是直角,即可判断的形状;
(2)根据等腰三角形的性质和勾股定理,得出,再利用勾股定理,即可求出的长.
【详解】(1)解:是等腰直角三角形,理由如下:
,,
,,
,
,
,
为的直径,
,
是等腰直角三角形;
(2)解:由(1)可知,是等腰直角三角形,
,
由勾股定理得:,
为的直径,
,
.
【点睛】本题考查了同弧所对的圆周角相等,直径所对的圆周角是直角,,等腰直角三角形的判定和性质,勾股定理,解题关键是掌握圆的相关性质是解题关键.
7.(1)见解析
(2)8
【分析】(1)由垂径定理,得到,进而得到,三线合一,得到,等边对等角,得到,即可得出;
(2)先求出的长,勾股定理求出的长,垂径定理得到即可.
【详解】(1)证明:∵是的直径,,
∴,
∴,
∵,
∴,
∵,
∴,
∴;
(2)∵的半径为5,,
∴,
∵,
∴,
∵是的直径,,
∴.
【点睛】本题考查垂径定理,勾股定理,中垂线的判定和性质,等腰三角形的判定和性质,熟练掌握垂径定理,是解题的关键.
8.(1)见解析
(2)
(3)
【分析】(1)根据是的直径,弦可得,从而得到,结合等腰三角形底边上三线合一可得,根据对顶角相等,等量代换,即可得出结论;
(2)根据圆周角定理可得,,结合可得,结合等腰三角形的性质,三角形内角和定理,即可得到答案;
(3)连接,,根据图形可得,则,,勾股定理即可得到
【详解】(1)解:是的“纯倍角”,理由如下:
如图所示,设交于点,
∵是的直径,,
∴,
∴
∴
∵
∴,
∴是的“纯倍角”
(2)∵弧的度数为,
∴
∵
∴,
∴
.
(3)根据图3可得,,则,
连接;
∴
∴
∵
∴
∴.
【点睛】本题考查圆周角定理,勾股定理,垂径定理,等腰直角三角形性质,解题的关键是作辅助线.
9.(1)见解析
(2)①理由见解析;②
【分析】本题考查了切线的判定、全等三角形的判定与性质、垂径定理、圆周角定义、平行线的性质、圆内接四边形、等腰三角形的判定以及勾股定理
(1)连接连接,,,由可证,利用全等三角形的性质可得出,即平分,利用垂径定理可得出,结合平行线性质可得,由此即可得出结论;
(2)连接,由圆内接四边形对角互补结合可得出,由同角的余角相等可得出,结合已知可得出,再利用等角对等腰可证出;由可证,利用全等三角形的性质可求出,的长,设在中,利用勾股定理即可求出结果.
【详解】(1)证明:如图1,连接,,,
在和中,
,
,
,
平分,
,
,
,
是的切线;
(2)①理由如下:
如图2,连接,
,
,
,
,
,
,
,
,
;
②在与中,
,
,
,,
设,在中,,,,
即,
解得:,
.
10.(1)见解析
(2)见解析
【分析】本题考查了圆中的无刻度直尺的尺规作图,熟练掌握圆的性质,正方形的判定,等边三角形的判定和性质是作图的关键.
(1)根据对角线互相垂直、平分且相等的四边形是正方形,画图即可.
(2)根据等边三角形的判定和性质,圆的性质,画图即可.
【详解】(1)根据对角线互相垂直、平分且相等的四边形是正方形,画图如下:
则四边形即为所求.
(2)1.作直径,连接,则,
∵,点在上,且,
∴,
∴是等边三角形,
∴,;
2.延长,二线交于点F,作直径,连接,交于点N,
则直线是的垂直平分线,
∴,
∴是等边三角形,
∴,
3.连接,则,
∴是等边三角形,
则即为所求.
11.(1)见解析
(2)为的切线,理由见解析
【分析】本题考查尺规作垂线,切线的性质和判定,等腰三角形的判定和性质.熟练掌握切线的性质,是解题的关键.
(1)运用过直线外一点作已知直线的垂线的方法作图即可;
(2)连接,则垂直平分,根据等边对等角得到,,既可以解题.
【详解】(1)如图,直线即为所作;
(2)连接,
∵,
∴,
又∵,
∴垂直平分,
∴,
∴,
又∵为的切线,
∴,
∴,
∴为的切线.
12.
【分析】本题主要考查扇形面积及垂径定理,连接交于点O,即为圆心,过圆心O作于点E,于点F, 由题意易得,然后根据勾股定理可求半径,进而可得劣弧及优弧的度数,最后问题可求解,熟练掌握扇形面积及垂径定理是解题的关键.
【详解】解:如图,连接交于点O,即为圆心,过圆心O作于点E,于点F,
∵,
∴,,
在中,,
∴,
∴,
∴优弧的度数为,
∴打掉墙体的面积为:,
∴要打掉的墙体面积为.
13.(1)该林区一颗这种树木平均根部横截面积为,平均材积量为.
(2)该林区这种树木的总材积量为.
【分析】(1)根据平均数的定义可直接求得答案.
(2)设树木的材积量与其根部横截面积的函数解析式为,根据(1)求得的结果可求得的数值,进而可求得答案.
【详解】(1)一颗这种树木平均根部横截面积.
一颗这种树木平均材积量.
答:该林区一颗这种树木平均根部横截面积为,平均材积量为.
(2)设树木的材积量与其根部横截面积的函数解析式为.
因为的图象经过点,得
.
解得
.
所以,树木的材积量与其根部横截面积的函数解析式为.
当时,.
答:该林区这种树木的总材积量为.
【点睛】本题主要考查平均数的定义以及采用待定系数法求一次函数解析式,牢记平均数的定义及求一次函数解析式的方法是解题的关键.
14.(1)
(2) 甲队队员身高更整齐
【分析】(1)根据中位数和众数的定义可直接求得答案.
(2)根据方差的定义可直接求得甲队的方差,方差越小,数据的波动越小,即可判断哪队队员身高更整齐.
【详解】(1)将甲队身高数据按从小到大的顺序排列,且数据个数为偶数,则中间两个数和的平均数为这组数据的中位数,即中位数.
乙队身高数据中,出现次数最多的数据为,所以这组数据的众数.
故答案为:
(2)
,所以甲队队员身高更整齐.
【点睛】本题主要考查中位数、众数、方差的定义,牢记中位数、众数、方差的定义是解题的关键.
15.(1)
(2)
【分析】(1)直接由概率公式求解即可;
(2)画树状图,共有9种等可能的结果,其中小明和小华都抽取到大雁塔图片的结果有1种,再由概率公式求解即可.
【详解】(1)解:小明随机抽取一张图片,则抽取到华山图片的概率是;
(2)画树状图如下:
共有9种等可能的结果,其中小明和小华都抽取到大雁塔图片的结果有1种,
∴他们都抽取到大雁塔图片的概率为 .
【点睛】此题考查的是用树状图法求概率.树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.
16.(1)见解析
(2)
【分析】(1)首先将立定跳远、掷实心球、一分钟跳绳和引体向上分别用,,,表示,然后画树状图,由树状图求得所有等可能的结果;
(2)首先根据题意列出表格,然后由表格求得所有等可能的结果与两名男生在体育测试中所选项目完全相同的情况,再利用概率公式求解即可求得答案.
【详解】(1)解:将立定跳远、掷实心球、一分钟跳绳和引体向上分别用,,,表示,
画树状图得:
可得可能选择的结果有四种:①1000米跑、立定跳远、一分钟跳绳;②1000米跑、立定跳远、引体向上;③1000米跑、掷实心球、一分钟跳绳;④1000米跑、掷实心球、引体向上;
(2)记:①1000米跑、立定跳远、一分钟跳绳;②1000米跑、立定跳远、引体向上;③1000米跑、掷实心球、一分钟跳绳;④1000米跑、掷实心球、引体向上;
列表得
① ② ③ ④
① ①,① ①,② ①,③ ①,④
② ②,① ②,② ②,③ ②,④
③ ③,① ③,② ③,③ ③,④
④ ④,① ④,② ④,③ ④,④
所有可能出现的结果共有16种,其中所选项目相同的有4种.
两人所选项目相同的概率为:.
【点睛】此题考查的是用列表法或树状图法求概率.注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率所求情况数与总情况数之比.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末解答题易错专项特训-2023-2024学年数学九年级上册苏教版
1.某商店准备销售一种多功能旅行背包,计划从厂家以每个30元的价格进货,经过市场调查发现当每个背包的售价为40元时,月均销量为280个,售价每增长2元,月均销量就相应减少20个.
(1)若使这种背包的月均销量不低于130个,每个背包售价应不高于多少元;
(2)在(1)的条件下,当这种背包销售单价为多少元时,销售利润是3120元?
(3)这种背包的销售利润有可能达到3700元吗?若能,请求出此时的销售单价;若不能,请说明理由.
2.为了喜迎杭州第十九届亚运会,某学校计划对一块宽为,长为的矩形荒地进行改造,要求修筑同样宽鹅卵石小路,余下的部分种上草坪(阴影部分),并使草坪的面积为.现在邀请全校同学参与设计,下面是三位同学分别设计的方案,请你选择一种方案,求出道路的宽为多少米?(根据需要精确到0.1米)
3.已知关于的一元二次方程(为常数).
(1)求证:不论为何值时,方程总有两个不相等的实数根.
(2)设是方程的两个根,且,求的值.
4.阅读下列材料:
利用完全平方公式,将多项式变形为的形式,
例如:.
根据以上材料,解答下列问题:
(1)填空:将多项式变形为的形式,并判断与0的大小关系,
;
所以 0(填“”、“”、“”;
(2)将多项式变形为的形式,并求出多项式的最小值;
(3)求证:、取任何实数时,多项式的值总为正数.
5.如图,在中,是直径,点是圆上一点,在的延长线上取一点,连接,使.求:
(1)求证:直线是的切线;
(2)若,求扇形的面积
6.如图,四边形内接于,为的直径,.
(1)试判断的形状,并说明理由;
(2)若,求的长.
7.如图,内接于,是的直径,,垂足为D.
(1)求证:;
(2)已知的半径为5,,求长.
8.如图①,,是半圆上的两点,若直径上存在一点,满足,则称是的“纯倍角”.
(1)如图②,是圆的直径,弦垂直于,是弧上一点,连结交于点,连结,是的“纯倍角”吗?请说明理由.
(2)在(1)的条件下,设弧的度数为,请用含的代数式表示和的度数.
(3)如图③,在(1)的条件下,连结,直径,.求弦的长.
9.如图,在四边形中,平分为的外接圆.
(1)如图1,求证:是的切线;
(2)如图2,交于点,过点作,垂足为,交于点.若,
①与的数量关系是 ;
②直接写出的长.
10.如图,的半径,点在上,且,请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹,不必写画法)
图1 图2
(1)在图1中,画出的一个内接正方形;
(2)在图2中,画出的一个内接等边三角形.
11.如图,为的切线,A为切点,直线交于点E,F.
(1)请用无刻度的直尺和圆规过点A作的垂线,垂足为D,交于点B.(保留作图痕迹,不写作法)
(2)连接,试判断与的位置关系,并给出证明.
12.一面墙上有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,如图,已知矩形的长为,宽为,求要打掉的墙体面积.
13.某地经过多年的环境治理,已将荒山改造成了绿水青山.为估计一林区某种树木的总材积量,随机选取了10棵这种树木,测量每棵树的根部横截面积(单位:)和材积量(单位:),得到如下数据:
样本号 1 2 3 4 5 6 7 8 9 10
根部横截面积x 0.04 0.06 0.04 0.08 0.08 0.05 0.05 0.07 0.07 0.06
材积量y 0.25 0.40 0.22 0.54 0.51 0.34 0.36 0.46 0.42 0.40
(1)估计该林区一颗这种树木平均根部横截面积与平均材积量.
(2)现测量了该林区部分这种树木的根部横截面积,经过测算得到这种树木的根部横截面积总和为.已知树木的材积量与其根部横截面积近似成正比.利用以上数据估计该林区这种树木的总材积量.
14.某中学的国旗护卫队需从甲、乙两队中选择一队身高比较整齐的队员担任护旗手,两队每个队员的身高(单位:cm)如下:
甲队 177 179 178 179 177 178 178 179 178 177
平均数 中位数 众数 方差
甲队 178 a 178 c
乙队 177.1 177 b 0.89
两组样本数据的平均数,中位数,众数,方差如表中数据所示:
(1)表中________,________.
(2)请计算甲队的方差c,并判断哪队队员身高更整齐.
15.陕西历史悠久,是中华文明的重要发祥地之一,有着众多的名胜古迹,其中华山、秦始皇陵和大雁塔等文明古迹堪称为国之瑰宝,吸引着国内外的游客来陕游玩.小明收集了华山、秦始皇陵、大雁塔这三个景点的图片各一张,这些图片大小、形状及背面完全相同,把这三张图片洗匀后背面朝上放置在桌面上(三张图片依次用A,B,C表示).
(1)小明随机抽取一张图片,则抽取到华山图片的概率是______;
(2)小明随机抽取一张图片后,放回洗匀,小华再随机抽取一张图片,请用列表或画树状图的方法求他们都抽取到大雁塔图片的概率.
16.某市今年中考体育测试,其中男生测试项目有1000米跑、立定跳远、掷实心球、一分钟跳绳、引体向上五个项目.考生须从这五个项目中选取三个项目,要求:1000米跑必选,立定跳远和掷实心球二选一,一分钟跳绳和引体向上二选一.
(1)写出男生在体育测试中所有可能选择的结果;
(2)请你用列表法或画树状图法,求出两名男生在体育测试中所选项目完全相同的概率.
参考答案:
1.(1)元
(2)元
(3)不能,理由见解析
【分析】本题考查了一元一次不等式的应用,一元二次方程的应用,一元二次方程根的判别式,根据题意正确的列等式、不等式是解题的关键
(1)设每个背包的售价为元,则月均销量为个,依题意,得:,计算求解即可;
(2)依题意,得:,计算求出满足要求的解即可;
(3)依题意,得:,整理,得:,由,可知该方程无解,然后作答即可.
【详解】(1)解:设每个背包的售价为元,则月均销量为个,
依题意,得:,
解得:,
答:每个背包售价应不高于元.
(2)解:依题意,得:,
整理,得:,
解得:,不合题意,舍去.
答:当这种背包销售单价为元时,销售利润是元.
(3)解:不能,理由如下:
依题意,得:,
整理,得:,
∴,
该方程无解,
答:这种背包的销售利润不可能达到元.
2.道路的宽为1米或道路的宽为2米或道路的宽为米.
【分析】此题主要考查一元二次方程的应用,利用平移把道路进行平移,再根据草地的面积公式列出一元二次方程即可求解,解题的关键是根据题意找到等量关系列出方程进行求解.
【详解】解:选择方案一
设道路的宽为米,根据题意可列方程:
,
整理得:,
解得:,(舍去),
答:道路的宽为1米;
选择方案二
设道路的宽为米,根据题意可列方程:
,
整理得:,
解得:,(舍去),
答:道路的宽为2米;
选择方案三
设道路的宽为米,根据题意可列方程:
,
整理得:,
解得:,(舍去);
答:道路的宽为米.
3.(1)详细见解析.
(2).
【分析】求出判别式的符号,进行判断即可.
利用一元二次方程的解的定义和根与系数的关系求解.
【详解】(1)
方程总有两个不相等的实数根.
(2)是方程的两个根
在中,
即:
解得:或
【点睛】本题考查根的判别式、根与系数的关系以及因式分解等,熟练掌握相关知识点是解题的关键.
4.(1)1;2;
(2)最小值为
(3)证明见解析
【分析】本题考查了配方法的应用,熟练掌握配方法是解题的关键;
(1)模仿题干的例题配方即可,利用平方的非负性与0比较大小;
(2)将多项式配方,根据平方的非负性求出多项式的最小值;
(3)对多项式进行配方即可证明多项式的值总为正数.
【详解】(1)解:
,
,
,
,
故答案为:1;2;;
(2)解:
,
,
当时,有最小值,最小值为;
(3)证明:
,
,,
,
、取任何实数时,多项式的值总为正数.
5.(1)见解析
(2)
【分析】(1)连接,得到,圆周角定理得到,得到,进而得到,即可;
(2)根据,得到,进而得到,进而得到,根据含30度角的直角三角形的性质,得到,求出半径的长,根据扇形的面积公式进行求解即可.
【详解】(1)证明:连接,则:,
∴,
∵是直径,
∴,
∴,
∵,
∴,即:,
∴,
∵是的半径,
∴直线是的切线;
(2)∵,,
∴,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∴扇形的面积为.
【点睛】本题考查切线的判定和性质,圆周角定理,扇形的面积,等边对等角,含30度角的直角三角形.熟练掌握相关知识点,灵活运用,是解题的关键.
6.(1)等腰直角三角形,理由见解析;
(2)
【分析】(1)根据同弧所对的圆周角相等,得到,,进而得到,再根据直径所对的圆周角是直角,即可判断的形状;
(2)根据等腰三角形的性质和勾股定理,得出,再利用勾股定理,即可求出的长.
【详解】(1)解:是等腰直角三角形,理由如下:
,,
,,
,
,
,
为的直径,
,
是等腰直角三角形;
(2)解:由(1)可知,是等腰直角三角形,
,
由勾股定理得:,
为的直径,
,
.
【点睛】本题考查了同弧所对的圆周角相等,直径所对的圆周角是直角,,等腰直角三角形的判定和性质,勾股定理,解题关键是掌握圆的相关性质是解题关键.
7.(1)见解析
(2)8
【分析】(1)由垂径定理,得到,进而得到,三线合一,得到,等边对等角,得到,即可得出;
(2)先求出的长,勾股定理求出的长,垂径定理得到即可.
【详解】(1)证明:∵是的直径,,
∴,
∴,
∵,
∴,
∵,
∴,
∴;
(2)∵的半径为5,,
∴,
∵,
∴,
∵是的直径,,
∴.
【点睛】本题考查垂径定理,勾股定理,中垂线的判定和性质,等腰三角形的判定和性质,熟练掌握垂径定理,是解题的关键.
8.(1)见解析
(2)
(3)
【分析】(1)根据是的直径,弦可得,从而得到,结合等腰三角形底边上三线合一可得,根据对顶角相等,等量代换,即可得出结论;
(2)根据圆周角定理可得,,结合可得,结合等腰三角形的性质,三角形内角和定理,即可得到答案;
(3)连接,,根据图形可得,则,,勾股定理即可得到
【详解】(1)解:是的“纯倍角”,理由如下:
如图所示,设交于点,
∵是的直径,,
∴,
∴
∴
∵
∴,
∴是的“纯倍角”
(2)∵弧的度数为,
∴
∵
∴,
∴
.
(3)根据图3可得,,则,
连接;
∴
∴
∵
∴
∴.
【点睛】本题考查圆周角定理,勾股定理,垂径定理,等腰直角三角形性质,解题的关键是作辅助线.
9.(1)见解析
(2)①理由见解析;②
【分析】本题考查了切线的判定、全等三角形的判定与性质、垂径定理、圆周角定义、平行线的性质、圆内接四边形、等腰三角形的判定以及勾股定理
(1)连接连接,,,由可证,利用全等三角形的性质可得出,即平分,利用垂径定理可得出,结合平行线性质可得,由此即可得出结论;
(2)连接,由圆内接四边形对角互补结合可得出,由同角的余角相等可得出,结合已知可得出,再利用等角对等腰可证出;由可证,利用全等三角形的性质可求出,的长,设在中,利用勾股定理即可求出结果.
【详解】(1)证明:如图1,连接,,,
在和中,
,
,
,
平分,
,
,
,
是的切线;
(2)①理由如下:
如图2,连接,
,
,
,
,
,
,
,
,
;
②在与中,
,
,
,,
设,在中,,,,
即,
解得:,
.
10.(1)见解析
(2)见解析
【分析】本题考查了圆中的无刻度直尺的尺规作图,熟练掌握圆的性质,正方形的判定,等边三角形的判定和性质是作图的关键.
(1)根据对角线互相垂直、平分且相等的四边形是正方形,画图即可.
(2)根据等边三角形的判定和性质,圆的性质,画图即可.
【详解】(1)根据对角线互相垂直、平分且相等的四边形是正方形,画图如下:
则四边形即为所求.
(2)1.作直径,连接,则,
∵,点在上,且,
∴,
∴是等边三角形,
∴,;
2.延长,二线交于点F,作直径,连接,交于点N,
则直线是的垂直平分线,
∴,
∴是等边三角形,
∴,
3.连接,则,
∴是等边三角形,
则即为所求.
11.(1)见解析
(2)为的切线,理由见解析
【分析】本题考查尺规作垂线,切线的性质和判定,等腰三角形的判定和性质.熟练掌握切线的性质,是解题的关键.
(1)运用过直线外一点作已知直线的垂线的方法作图即可;
(2)连接,则垂直平分,根据等边对等角得到,,既可以解题.
【详解】(1)如图,直线即为所作;
(2)连接,
∵,
∴,
又∵,
∴垂直平分,
∴,
∴,
又∵为的切线,
∴,
∴,
∴为的切线.
12.
【分析】本题主要考查扇形面积及垂径定理,连接交于点O,即为圆心,过圆心O作于点E,于点F, 由题意易得,然后根据勾股定理可求半径,进而可得劣弧及优弧的度数,最后问题可求解,熟练掌握扇形面积及垂径定理是解题的关键.
【详解】解:如图,连接交于点O,即为圆心,过圆心O作于点E,于点F,
∵,
∴,,
在中,,
∴,
∴,
∴优弧的度数为,
∴打掉墙体的面积为:,
∴要打掉的墙体面积为.
13.(1)该林区一颗这种树木平均根部横截面积为,平均材积量为.
(2)该林区这种树木的总材积量为.
【分析】(1)根据平均数的定义可直接求得答案.
(2)设树木的材积量与其根部横截面积的函数解析式为,根据(1)求得的结果可求得的数值,进而可求得答案.
【详解】(1)一颗这种树木平均根部横截面积.
一颗这种树木平均材积量.
答:该林区一颗这种树木平均根部横截面积为,平均材积量为.
(2)设树木的材积量与其根部横截面积的函数解析式为.
因为的图象经过点,得
.
解得
.
所以,树木的材积量与其根部横截面积的函数解析式为.
当时,.
答:该林区这种树木的总材积量为.
【点睛】本题主要考查平均数的定义以及采用待定系数法求一次函数解析式,牢记平均数的定义及求一次函数解析式的方法是解题的关键.
14.(1)
(2) 甲队队员身高更整齐
【分析】(1)根据中位数和众数的定义可直接求得答案.
(2)根据方差的定义可直接求得甲队的方差,方差越小,数据的波动越小,即可判断哪队队员身高更整齐.
【详解】(1)将甲队身高数据按从小到大的顺序排列,且数据个数为偶数,则中间两个数和的平均数为这组数据的中位数,即中位数.
乙队身高数据中,出现次数最多的数据为,所以这组数据的众数.
故答案为:
(2)
,所以甲队队员身高更整齐.
【点睛】本题主要考查中位数、众数、方差的定义,牢记中位数、众数、方差的定义是解题的关键.
15.(1)
(2)
【分析】(1)直接由概率公式求解即可;
(2)画树状图,共有9种等可能的结果,其中小明和小华都抽取到大雁塔图片的结果有1种,再由概率公式求解即可.
【详解】(1)解:小明随机抽取一张图片,则抽取到华山图片的概率是;
(2)画树状图如下:
共有9种等可能的结果,其中小明和小华都抽取到大雁塔图片的结果有1种,
∴他们都抽取到大雁塔图片的概率为 .
【点睛】此题考查的是用树状图法求概率.树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.
16.(1)见解析
(2)
【分析】(1)首先将立定跳远、掷实心球、一分钟跳绳和引体向上分别用,,,表示,然后画树状图,由树状图求得所有等可能的结果;
(2)首先根据题意列出表格,然后由表格求得所有等可能的结果与两名男生在体育测试中所选项目完全相同的情况,再利用概率公式求解即可求得答案.
【详解】(1)解:将立定跳远、掷实心球、一分钟跳绳和引体向上分别用,,,表示,
画树状图得:
可得可能选择的结果有四种:①1000米跑、立定跳远、一分钟跳绳;②1000米跑、立定跳远、引体向上;③1000米跑、掷实心球、一分钟跳绳;④1000米跑、掷实心球、引体向上;
(2)记:①1000米跑、立定跳远、一分钟跳绳;②1000米跑、立定跳远、引体向上;③1000米跑、掷实心球、一分钟跳绳;④1000米跑、掷实心球、引体向上;
列表得
① ② ③ ④
① ①,① ①,② ①,③ ①,④
② ②,① ②,② ②,③ ②,④
③ ③,① ③,② ③,③ ③,④
④ ④,① ④,② ④,③ ④,④
所有可能出现的结果共有16种,其中所选项目相同的有4种.
两人所选项目相同的概率为:.
【点睛】此题考查的是用列表法或树状图法求概率.注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率所求情况数与总情况数之比.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
