冀教版八下数学第二十章《回顾与反思》复习(共14张PPT)
文档属性
| 名称 | 冀教版八下数学第二十章《回顾与反思》复习(共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 190.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-09 16:14:17 | ||
图片预览






文档简介
课件14张PPT。 函数复习第二十章一、知识要点: 1、一次函数的概念:函数y=_______(k、b为常数,k______)叫做一次函数。当b_____时,函数y=____(k____)叫做正比例函数。kx +b≠0 = 0≠0kx★理解一次函数概念应注意下面两点:
⑴、解析式中自变量x的次数是___次,⑵、比例系数_____。1K≠0 2、正比例函数y=kx(k≠0)的图象是过点(_____),(______)的_________。
3、一次函数y=kx+b(k≠0)的图象是过点(0,___),(____,0)的__________。0,01,k 一条直线b一条直线4、正比例函数y=kx(k≠0)的性质:
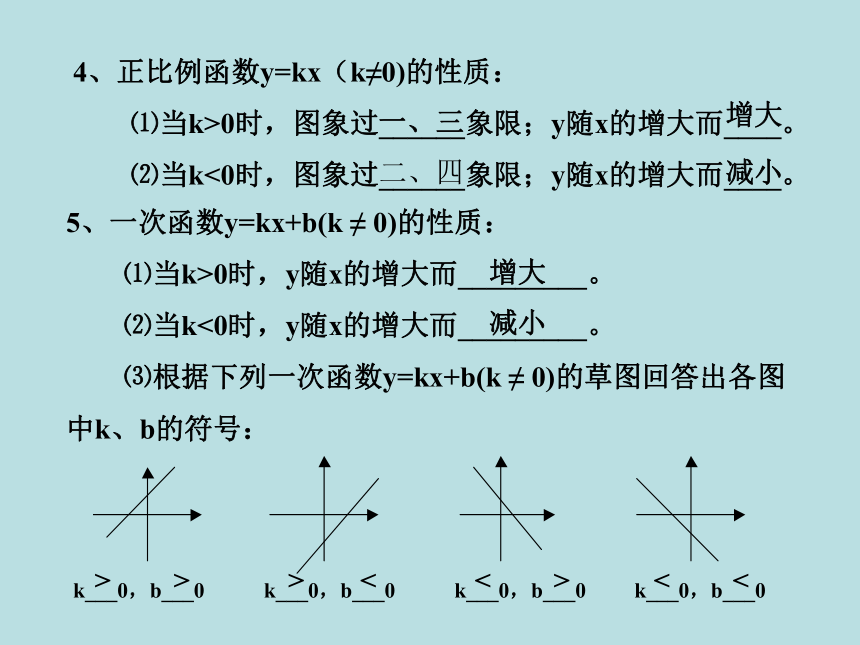
⑴当k>0时,图象过______象限;y随x的增大而____。
⑵当k<0时,图象过______象限;y随x的增大而____。一、三增大二、四减小5、一次函数y=kx+b(k ≠ 0)的性质:
⑴当k>0时,y随x的增大而_________。
⑵当k<0时,y随x的增大而_________。
⑶根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图
中k、b的符号:增大减小k___0,b___0 k___0,b___0 k___0,b___0 k___0,b___0<<><<>>>二、范例。
例1 填空题:
(1) 有下列函数:① , ② ,
③ , ④ 。其中过原点的直
线是_____;函数y随x的增大而增大的是___________;函数y随x的增大而减小的是______;图象在第一、二、三象限的是_____。②①、②、③④③ (2)、如果一次函数y=kx-3k+6的图象经过原点,那么
k的值为________。
(3)、已知y-1与x成正比例,且x=-2时,y=4,那么y与
x之间的函数关系式为_________________。
k=2解:一次函数当x=1时,y=5。且它的图象与x轴交点
是(6,0)。由题意得解得∴一次函数的解析式为 y= - x+6。点评:用待定系数法求一次函数y=kx+b的解析式,可由已知条件给出的两对x、y的值,列出关于k、b的二元一次方程组。由此求出k、b的值,就可以得到所求的一次函数的解析式。例2、已知一次函数y=kx+b(k≠0)在x=1时,y=5,且
它的图象与x轴交点的横坐标是6,求这个一次函数的
解析式。 例3 柴油机在工作时油箱中的余油量Q(千克)
与工作时间t(小时)成一次函数关系,当工作开始时
油箱中有油40千克,工作3.5小时后,油箱中余油22.5
千克(1)写出余油量Q与时间t的函数关系式;(2)画出
这个函数的图象。解:(1)设Q=kt+b。把t=0,Q=40;t=3.5,Q=22.5
分别代入上式,得解得解析式为:Q=-5t+40 (0≤t≤8)(2)、取t=0,得Q=40;取t=8,得Q=0。描出点
A(0,40),B(8,0)。然后连成线段AB即是所
求的图形。点评:(1)求出函数关系式时,
必须找出自变量的取值范围。
(2)画函数图象时,应
根据函数自变量的取值范围来
确定图象的范围。20图象是包括
两端点的线段..AB1、在下列函数中, x是自变量, y是x的函数, 那些是一次函数?那些是正比例函数?
y=2x y=-3x+1 y=x22、某函数具有下列两条性质
(1)它的图像是经过原点(0,0)的一条直线;
(2)y的值随x值的增大而增大。
请你举出一个满足上述条件的函数(用关系式表示)3、函数 的图像与x轴交点坐标为________,
与y轴的交点坐标为____________。6、若函数y=kx+b的图像经过点(-3,-2)和(1,6)
求k、b及函数关系式。4、(1)对于函数y=5x+6,y的值随x值的减小而___。
(2)对于函数 , y的值随x值的____而增大。 5、直线y=kx+b过点(1,3)和点(-1,1),则
=__________。7、已知一次函数y=kx+b的图象经过A(a,6),B(4,b)
两点。a,b是一元二次方程 的两根,且b(1)、求这个一次函数的解析式。(2)在坐标平面内画
出这个函数的图象。
10、已知函数 问当m为何值时,它是一次函数?8、在直角坐标系中,一次函数y=kx+b的图像经过三
点A(2,0)、B(0,2)、C(m,3),求这个函数
的关系式,并求m的值。9、已知一次函数的图像经过点A(2,-1)和点B,
其中点B是另一条直线 与y轴的交点,求这
个一次函数的表达式。11、如果 是正比例函数,而且对于它的每一组非零的对应值(x,y)有xy<0,求m的值。12、如果y+3与x+2成正比例,且x=3时,y=7
(1)写出y与x之间的函数关系式;
(2)求当x=-1时,y的值;
(3)求当y=0时,x的值。13、已知:y+b与x+a(a,b是常数)成正比例。
求证:y是x的一次函数。14、为了加强公民的节水意识,合理利用水资源,某城
市规定用水标准如下:每户每月用水量不超过6米3时,水费按0.6元/米3收费,每户每月用水量超过6米3时,超过的部分按1元/米3。设每户每月用水量为x米3,应缴纳y元。
(1)写出每户每月用水量不超过6米3和每户每月用水量
超过6米3时,y与x之间的函数关系式,并判断它们是否为
一次函数。
(2)已知某户5月份的用水量为米3,求该用户5月份的水费。15、某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后。
(1)服药后______时,血液中含药量最高,
达到每毫升_______毫克,接着逐步衰弱。
(2)服药5时,血液中含药量为每毫升____毫克。
(3)当x≤2时y与x之间的函数关系式是_____。
(4)当x≥2时y与x之间的函数关系式是____。
(5)如果每毫升血液中含药量3毫克或3毫克以上
时,治疗疾病最有效,那么这个有效时间范围是___时。.
⑴、解析式中自变量x的次数是___次,⑵、比例系数_____。1K≠0 2、正比例函数y=kx(k≠0)的图象是过点(_____),(______)的_________。
3、一次函数y=kx+b(k≠0)的图象是过点(0,___),(____,0)的__________。0,01,k 一条直线b一条直线4、正比例函数y=kx(k≠0)的性质:
⑴当k>0时,图象过______象限;y随x的增大而____。
⑵当k<0时,图象过______象限;y随x的增大而____。一、三增大二、四减小5、一次函数y=kx+b(k ≠ 0)的性质:
⑴当k>0时,y随x的增大而_________。
⑵当k<0时,y随x的增大而_________。
⑶根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图
中k、b的符号:增大减小k___0,b___0 k___0,b___0 k___0,b___0 k___0,b___0<<><<>>>二、范例。
例1 填空题:
(1) 有下列函数:① , ② ,
③ , ④ 。其中过原点的直
线是_____;函数y随x的增大而增大的是___________;函数y随x的增大而减小的是______;图象在第一、二、三象限的是_____。②①、②、③④③ (2)、如果一次函数y=kx-3k+6的图象经过原点,那么
k的值为________。
(3)、已知y-1与x成正比例,且x=-2时,y=4,那么y与
x之间的函数关系式为_________________。
k=2解:一次函数当x=1时,y=5。且它的图象与x轴交点
是(6,0)。由题意得解得∴一次函数的解析式为 y= - x+6。点评:用待定系数法求一次函数y=kx+b的解析式,可由已知条件给出的两对x、y的值,列出关于k、b的二元一次方程组。由此求出k、b的值,就可以得到所求的一次函数的解析式。例2、已知一次函数y=kx+b(k≠0)在x=1时,y=5,且
它的图象与x轴交点的横坐标是6,求这个一次函数的
解析式。 例3 柴油机在工作时油箱中的余油量Q(千克)
与工作时间t(小时)成一次函数关系,当工作开始时
油箱中有油40千克,工作3.5小时后,油箱中余油22.5
千克(1)写出余油量Q与时间t的函数关系式;(2)画出
这个函数的图象。解:(1)设Q=kt+b。把t=0,Q=40;t=3.5,Q=22.5
分别代入上式,得解得解析式为:Q=-5t+40 (0≤t≤8)(2)、取t=0,得Q=40;取t=8,得Q=0。描出点
A(0,40),B(8,0)。然后连成线段AB即是所
求的图形。点评:(1)求出函数关系式时,
必须找出自变量的取值范围。
(2)画函数图象时,应
根据函数自变量的取值范围来
确定图象的范围。20图象是包括
两端点的线段..AB1、在下列函数中, x是自变量, y是x的函数, 那些是一次函数?那些是正比例函数?
y=2x y=-3x+1 y=x22、某函数具有下列两条性质
(1)它的图像是经过原点(0,0)的一条直线;
(2)y的值随x值的增大而增大。
请你举出一个满足上述条件的函数(用关系式表示)3、函数 的图像与x轴交点坐标为________,
与y轴的交点坐标为____________。6、若函数y=kx+b的图像经过点(-3,-2)和(1,6)
求k、b及函数关系式。4、(1)对于函数y=5x+6,y的值随x值的减小而___。
(2)对于函数 , y的值随x值的____而增大。 5、直线y=kx+b过点(1,3)和点(-1,1),则
=__________。7、已知一次函数y=kx+b的图象经过A(a,6),B(4,b)
两点。a,b是一元二次方程 的两根,且b
出这个函数的图象。
10、已知函数 问当m为何值时,它是一次函数?8、在直角坐标系中,一次函数y=kx+b的图像经过三
点A(2,0)、B(0,2)、C(m,3),求这个函数
的关系式,并求m的值。9、已知一次函数的图像经过点A(2,-1)和点B,
其中点B是另一条直线 与y轴的交点,求这
个一次函数的表达式。11、如果 是正比例函数,而且对于它的每一组非零的对应值(x,y)有xy<0,求m的值。12、如果y+3与x+2成正比例,且x=3时,y=7
(1)写出y与x之间的函数关系式;
(2)求当x=-1时,y的值;
(3)求当y=0时,x的值。13、已知:y+b与x+a(a,b是常数)成正比例。
求证:y是x的一次函数。14、为了加强公民的节水意识,合理利用水资源,某城
市规定用水标准如下:每户每月用水量不超过6米3时,水费按0.6元/米3收费,每户每月用水量超过6米3时,超过的部分按1元/米3。设每户每月用水量为x米3,应缴纳y元。
(1)写出每户每月用水量不超过6米3和每户每月用水量
超过6米3时,y与x之间的函数关系式,并判断它们是否为
一次函数。
(2)已知某户5月份的用水量为米3,求该用户5月份的水费。15、某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后。
(1)服药后______时,血液中含药量最高,
达到每毫升_______毫克,接着逐步衰弱。
(2)服药5时,血液中含药量为每毫升____毫克。
(3)当x≤2时y与x之间的函数关系式是_____。
(4)当x≥2时y与x之间的函数关系式是____。
(5)如果每毫升血液中含药量3毫克或3毫克以上
时,治疗疾病最有效,那么这个有效时间范围是___时。.
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
