冀教版八下数学20.4函数的初步应用 课件(共18张PPT)
文档属性
| 名称 | 冀教版八下数学20.4函数的初步应用 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 848.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-09 16:24:27 | ||
图片预览

文档简介
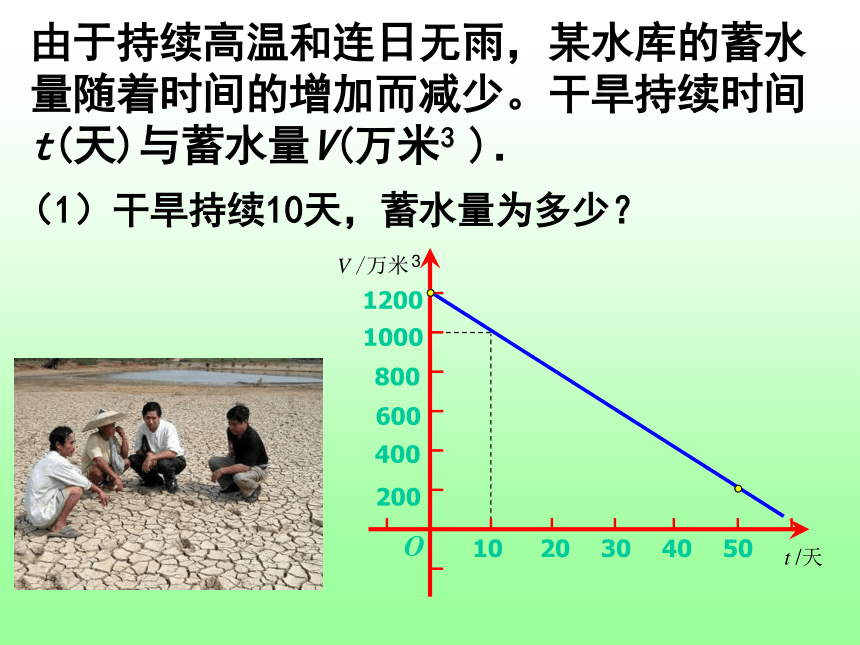
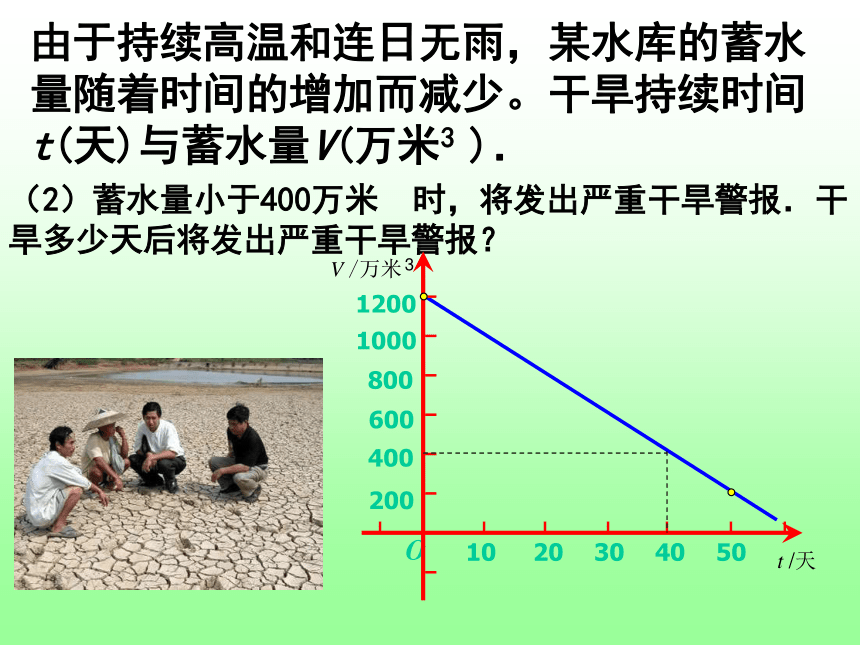
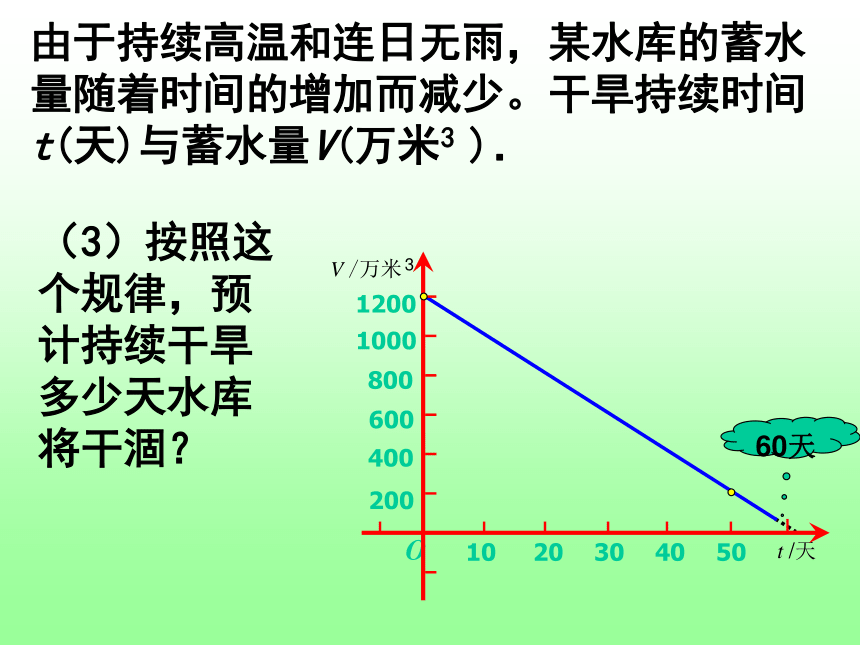
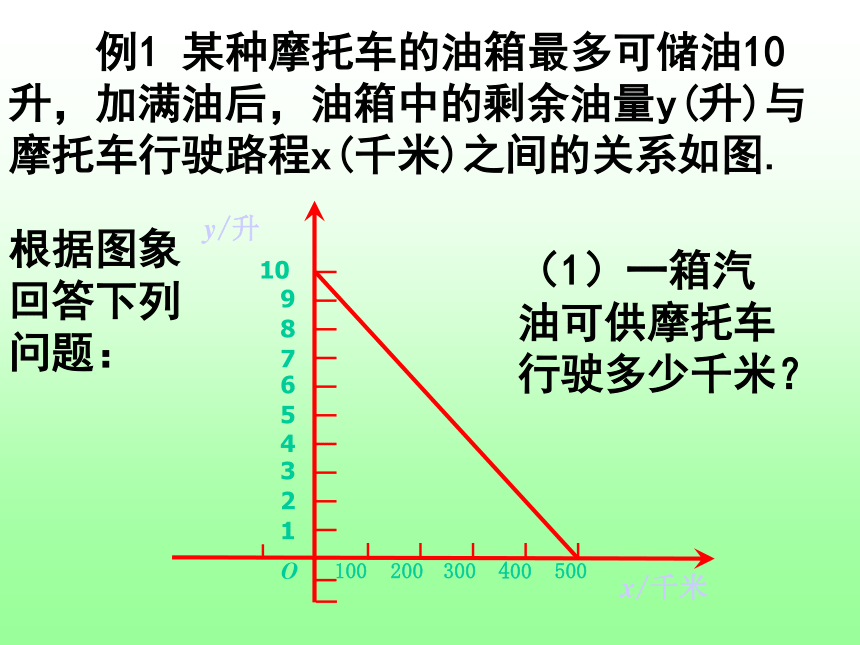
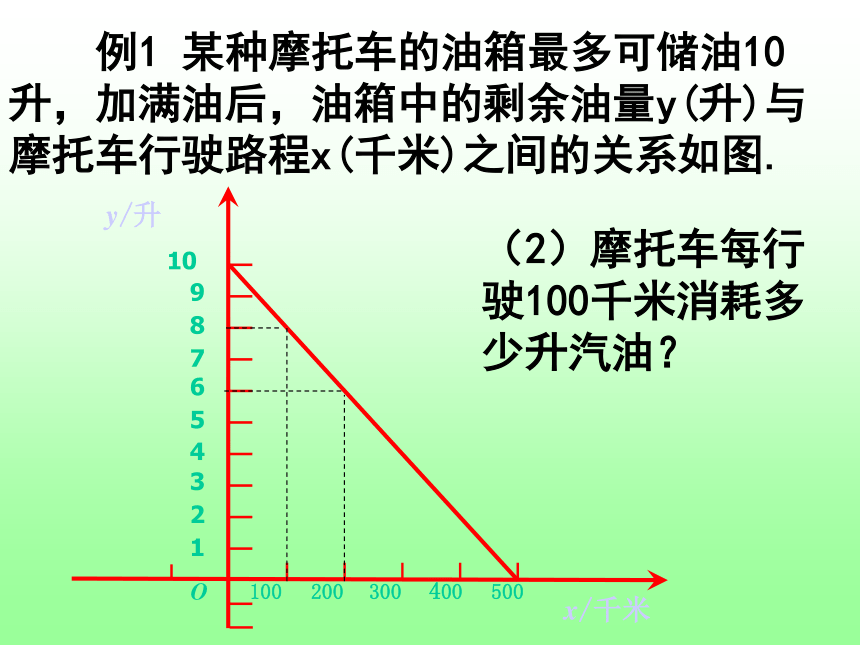
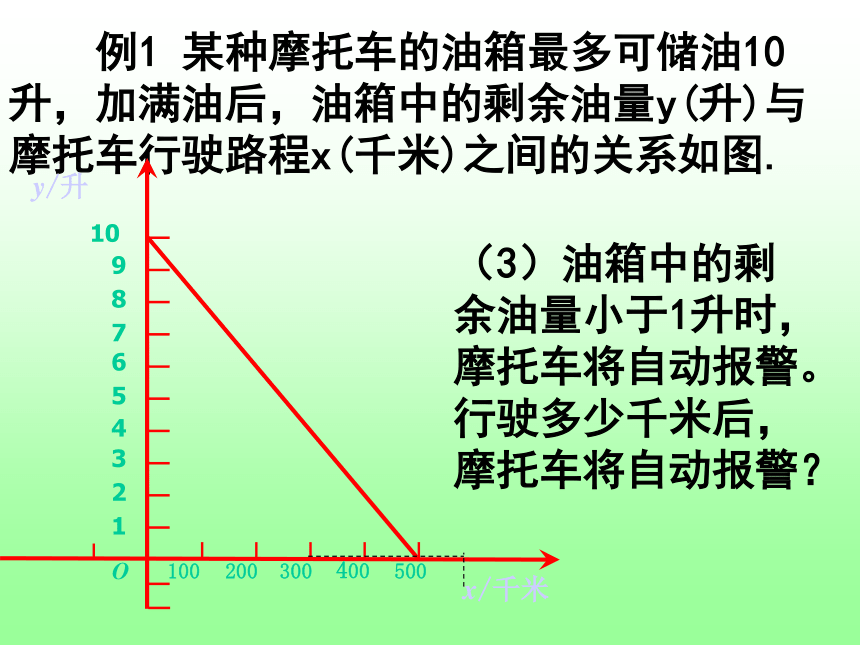
课件18张PPT。函数的初步应用由于持续高温和连日无雨,某水库的蓄水量随着时间的增加而减少。干旱持续时间t(天)与蓄水量V(万米3 ).(1)干旱持续10天,蓄水量为多少?(2)蓄水量小于400万米 时,将发出严重干旱警报.干旱多少天后将发出严重干旱警报?3由于持续高温和连日无雨,某水库的蓄水量随着时间的增加而减少。干旱持续时间t(天)与蓄水量V(万米3 ).(3)按照这个规律,预计持续干旱多少天水库将干涸?60天由于持续高温和连日无雨,某水库的蓄水量随着时间的增加而减少。干旱持续时间t(天)与蓄水量V(万米3 ). 例1 某种摩托车的油箱最多可储油10升,加满油后,油箱中的剩余油量y(升)与摩托车行驶路程x(千米)之间的关系如图.根据图象回答下列问题:(1)一箱汽油可供摩托车行驶多少千米? 例1 某种摩托车的油箱最多可储油10升,加满油后,油箱中的剩余油量y(升)与摩托车行驶路程x(千米)之间的关系如图.(2)摩托车每行驶100千米消耗多少升汽油? 例1 某种摩托车的油箱最多可储油10升,加满油后,油箱中的剩余油量y(升)与摩托车行驶路程x(千米)之间的关系如图.(3)油箱中的剩余油量小于1升时,摩托车将自动报警。行驶多少千米后,摩托车将自动报警? 下图是雷达追踪战斧式导弹发射后,导弹允许飞行时飞行的距离与时间的图象,若此时目标距离发射点2000公里,试确定匀速飞行后多长时间击中目标?看下面的四个图象如何确定一次函数y=kx+b(k≠0)中k、b的符号。某气象研究中心观测一场沙尘暴从发生到结束的全过程,开始时风速平均每小时增加2千米,4小时后沙尘暴经过开阔荒漠地,风速变为平均每小时增加4千米,一段时间,风速保持不变,当沙尘暴遇到绿色植被区时,其风速平均每小时减少1千米,最终停止,结合风速与时间的图像同,回答下列问题:?
(1)在y轴( )内填入相应的数值;
(2)沙尘暴从发生到结束,共经过多少小时?
(3)求出当x≥25时,风速y(千米/时)与时间x (小时)之间的函数关系式;甲、乙两家体育用品商店出售同样的乒乓球拍和乒乓球,乒乓球拍每副定价20元,乒乓球每盒定价5元。现两家商店搞促销活动,甲店:每买一副球拍赠送一盒乒乓球;乙店:按定价的9折优惠。某班级需购球拍4副,乒乓球若干盒(不少于4盒)。(1)设购买乒乓球盒数为x,在甲店购买的付款数为y甲(元),在乙店购买的付款数为y乙元),分别写出在两家商店购买的付款数与乒乓球数x之间的函数关系式;
(2)就乒乓球盒数讨论去哪家商店购买合算? 图10表示一骑自行车和一骑摩托车沿相同路由甲地到乙地行驶过程的函数图像(分别为正比例函数和一次函数).两地间的距离是80千米.请你根据图像回答或解决下面的问题:
(1)谁出发的较早?早多长时间?谁到达乙地较早?早到多长时间?
(2)两人在途中行驶的速度分别是多少?
(3)请你分别求出表示自行车和摩托车行驶过程的函数解析式(不要求写出自变量的取植范围);(4) 指出在什么时间段内两车均行驶在途中(不包括端点);在这一时间段内,请你分别按下列条件列出关于时间x的方程或不等式(不要化简,也不要求解):①自行车行驶在摩托车前面;②自行车与摩托车相遇;③自行车行驶在摩托车后面。
????? 在某地,人们发现某种蟋蟀1分钟所叫次数与当地温度之间近似为一次函数关系。下面是蟋蟀所叫次数与温度变化情况对照表:
(1)根据表中数据确定该一次函数的关系式;(2)如果蟋蟀1分钟叫了63次,那么该地当时的温度大约为多少摄氏度?
1.?????
?
小明同学骑自行车去郊外春游,下图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象.(1)根据图象回答:小明到达离家最远的地方需几小时?此时离家多远?(2)求小明出发两个半小时离家多远?(3)求小明出发多长时间距家12千米?
(1)在y轴( )内填入相应的数值;
(2)沙尘暴从发生到结束,共经过多少小时?
(3)求出当x≥25时,风速y(千米/时)与时间x (小时)之间的函数关系式;甲、乙两家体育用品商店出售同样的乒乓球拍和乒乓球,乒乓球拍每副定价20元,乒乓球每盒定价5元。现两家商店搞促销活动,甲店:每买一副球拍赠送一盒乒乓球;乙店:按定价的9折优惠。某班级需购球拍4副,乒乓球若干盒(不少于4盒)。(1)设购买乒乓球盒数为x,在甲店购买的付款数为y甲(元),在乙店购买的付款数为y乙元),分别写出在两家商店购买的付款数与乒乓球数x之间的函数关系式;
(2)就乒乓球盒数讨论去哪家商店购买合算? 图10表示一骑自行车和一骑摩托车沿相同路由甲地到乙地行驶过程的函数图像(分别为正比例函数和一次函数).两地间的距离是80千米.请你根据图像回答或解决下面的问题:
(1)谁出发的较早?早多长时间?谁到达乙地较早?早到多长时间?
(2)两人在途中行驶的速度分别是多少?
(3)请你分别求出表示自行车和摩托车行驶过程的函数解析式(不要求写出自变量的取植范围);(4) 指出在什么时间段内两车均行驶在途中(不包括端点);在这一时间段内,请你分别按下列条件列出关于时间x的方程或不等式(不要化简,也不要求解):①自行车行驶在摩托车前面;②自行车与摩托车相遇;③自行车行驶在摩托车后面。
????? 在某地,人们发现某种蟋蟀1分钟所叫次数与当地温度之间近似为一次函数关系。下面是蟋蟀所叫次数与温度变化情况对照表:
(1)根据表中数据确定该一次函数的关系式;(2)如果蟋蟀1分钟叫了63次,那么该地当时的温度大约为多少摄氏度?
1.?????
?
小明同学骑自行车去郊外春游,下图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象.(1)根据图象回答:小明到达离家最远的地方需几小时?此时离家多远?(2)求小明出发两个半小时离家多远?(3)求小明出发多长时间距家12千米?
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
