安徽省合肥市寿春中学2023--2024学年上学期九年级数学12月份教学质量检测卷(无答案)
文档属性
| 名称 | 安徽省合肥市寿春中学2023--2024学年上学期九年级数学12月份教学质量检测卷(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 389.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-10 17:26:30 | ||
图片预览


文档简介
安徽省合肥市寿春中学九年级12月份教学质量检测卷
班级: 姓名:
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列图案中,既是轴对称图形又是中心对称图形的是…………………………………………………【 】
A. B. C. D.
2.若锐角A满足cosA=,则∠A的度数是……………………………………………………………【 】
A.15° B.30° C.45° D.60°
3.如图,△ABC∽△DEF,AB:DE=1:2,则下列等式一定成立的是……………………………………【 】
A.= B.= C.= D.=
4.如图,已知在⊙O中,BC是直径,AB=DC,则下列结论不一定成立的是……………………………【 】
A. B.∠AOB=∠COD
C.OA=OB=AB D.O到AB、CD的距离相等
5.如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示出sinα的值,正确的是………………………………………………………………………………………………【 】
A. B. C. D.
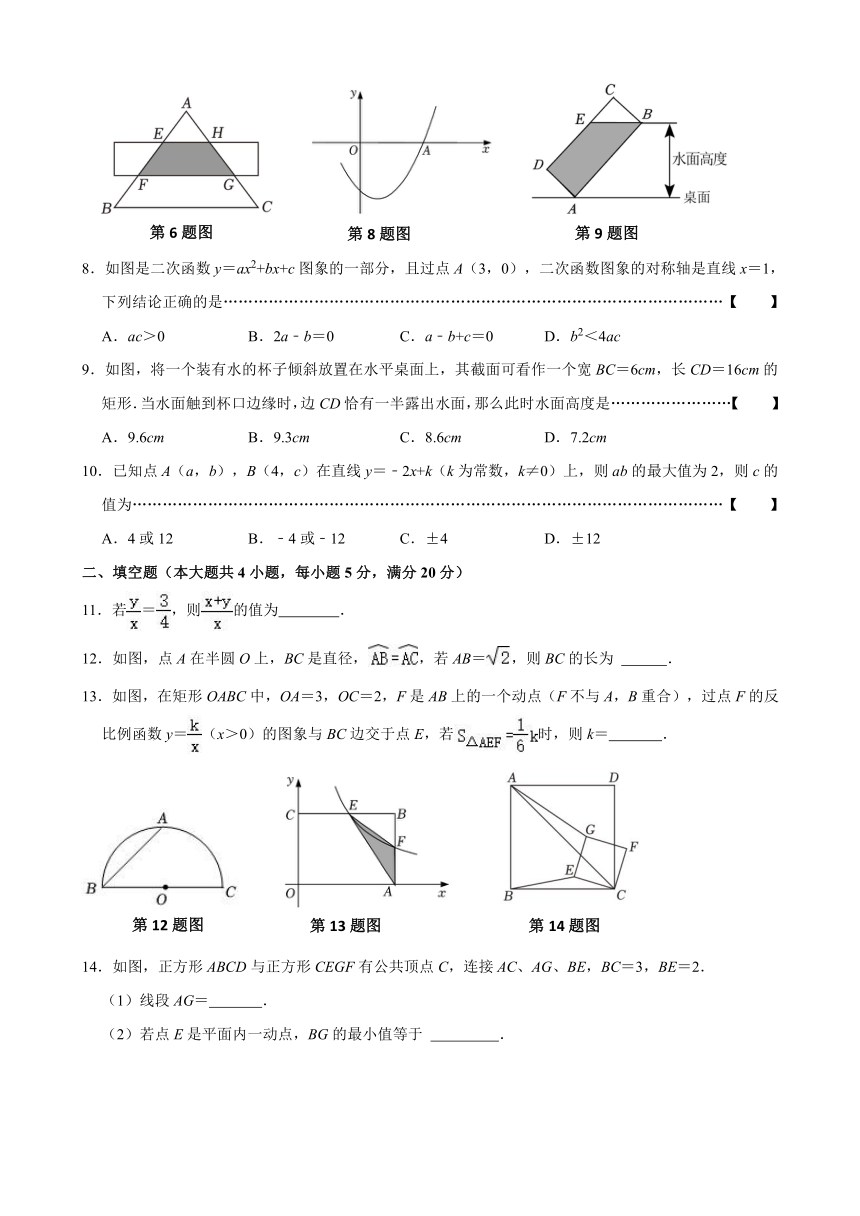
6.如图,△ABC是等边三角形,被一平行于BC的矩形所截,AB被截成三等分,则图中阴影部分的面积是△ABC的面积的………………………………………………………………………………………【 】
A. B. C. D.
7.下列语句中不正确的有…………………………………………………………………………………【 】
①相等的圆心角所对的弧相等;②平分弦的直径垂直于弦;③圆是轴对称图形,任何一条直径所在直线都是它的对称轴;④长度相等的两条弧是等弧.
A.3个 B.2个 C.1个 D.以上都不对
8.如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是直线x=1,下列结论正确的是………………………………………………………………………………………【 】
A.ac>0 B.2a﹣b=0 C.a﹣b+c=0 D.b2<4ac
9.如图,将一个装有水的杯子倾斜放置在水平桌面上,其截面可看作一个宽BC=6cm,长CD=16cm的矩形.当水面触到杯口边缘时,边CD恰有一半露出水面,那么此时水面高度是……………………【 】
A.9.6cm B.9.3cm C.8.6cm D.7.2cm
10.已知点A(a,b),B(4,c)在直线y=﹣2x+k(k为常数,k≠0)上,则ab的最大值为2,则c的值为………………………………………………………………………………………………………【 】
A.4或12 B.﹣4或﹣12 C.±4 D.±12
二、填空题(本大题共4小题,每小题5分,满分20分)
11.若=,则的值为 .
12.如图,点A在半圆O上,BC是直径,,若AB=,则BC的长为 .
13.如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=(x>0)的图象与BC边交于点E,若时,则k= .
14.如图,正方形ABCD与正方形CEGF有公共顶点C,连接AC、AG、BE,BC=3,BE=2.
(1)线段AG= .
(2)若点E是平面内一动点,BG的最小值等于 .
我们周五一起做练习
班级: 姓名:
一、选择题(本大题共10小题,每小题4分,满分40分) 12345678910
二、填空题(本大题共4小题,每小题5分,满分20分) 11. . 12. . 13. . 14.(1) ;(2) .
三、解答题(本大题共2小题,每小题8分,满分16分) 15.计算:.
16.如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1). (1)在图中以点O为位似中心在原点的另一侧画出△ABC放大2倍后得到的△A1B1C1,并写出A1的坐标; (2)请在图中画出△ABC绕点O逆时针旋转90°后得到的△A2B2C2.
四、解答题(本大题共2小题,每小题8分,满分16分) 17.已知抛物线y=x2﹣4x+7与y=x交于A、B两点(A在B点左侧). (1)请求出y<y时x的取值范围; (2)求抛物线顶点C的坐标,并求△ABC面积.
18.已知,如图,AB∥DC,∠ABC+∠ADB=180°. (1)求证:△ABD∽△BDC; (2)若AE平分∠DAB,BF平分∠DBC,且BF=2AE,S△ABD=3,求S△BDC.
五、解答题(本大题共2小题,每小题10分,满分20分) 19.如图所示的拱桥,用表示桥拱. (1)若所在圆的圆心为O,EF是弦CD的垂直平分线,请你利用尺规作图,找出圆心O.(不写作法,但要保留作图痕迹) 若拱桥的跨度AB的长为16m,拱高(的中点到弦AB的距离)为4m,求拱桥的半径R.
20.如图,某大楼的顶部竖有一块广告牌CD,小明与同学们在山坡的坡脚A处测得广告牌底部D的仰角为53°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:,AB=10米,AE=21米.(测角器的高度忽略不计,结果精确到0.1米,参考数据:≈1.41,≈1.73,sin53°≈,cos53°≈,tan53°≈) (1)求点B距水平地面AE的高度; (2)求广告牌CD的高度.(结果精确到0.1米)
六、(本题满分12分) 21.如图,⊙O是△ABC的外接圆,AE平分△ABC的外角∠DAC,OM⊥AB,ON⊥AC,垂足分别是点M、N,且OM=ON. (1)求证:AE∥BC; (2)如图,延长ON交AE于E点,若OE=7,ON=1,求⊙O的半径长.
七、(本题满分12分) 22.某公司销售一种商品,成本为每件30元,经过市场调查发现,该商品的日销售量y(件)与销售单价x(元)是一次函数关系,其销售单价、日销售量的三组对应数值如下表: 销售单价x(元)406080日销售量y(件)806040
(1)求日销售量y(件)与销售单价x(元)的函数关系式; (2)求公司销售该商品获得的最大日利润; (3)销售一段时间以后,由于某种原因,该商品每件成本增加了10元,若物价部门规定该商品销售单价不能超过a元,在日销售量y(件)与销售单价x(元)保持(1)中函数关系不变的情况下,该商品的日销售最大利润是1500元,求a的值.
八、(本题满分14分) 23.(1)如图1,正方形ABCD中,点E,F分别是AD、AB边上,且BE⊥CF于点O, 求证:BE=CF. (2)如图2,在(1)的条件下,连接AO并延长交BC于点G,若点G为BC边中点, 求证:AO2=AF AB. (3)在(2)的条件下,求tan∠ABE的值.
班级: 姓名:
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列图案中,既是轴对称图形又是中心对称图形的是…………………………………………………【 】
A. B. C. D.
2.若锐角A满足cosA=,则∠A的度数是……………………………………………………………【 】
A.15° B.30° C.45° D.60°
3.如图,△ABC∽△DEF,AB:DE=1:2,则下列等式一定成立的是……………………………………【 】
A.= B.= C.= D.=
4.如图,已知在⊙O中,BC是直径,AB=DC,则下列结论不一定成立的是……………………………【 】
A. B.∠AOB=∠COD
C.OA=OB=AB D.O到AB、CD的距离相等
5.如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示出sinα的值,正确的是………………………………………………………………………………………………【 】
A. B. C. D.
6.如图,△ABC是等边三角形,被一平行于BC的矩形所截,AB被截成三等分,则图中阴影部分的面积是△ABC的面积的………………………………………………………………………………………【 】
A. B. C. D.
7.下列语句中不正确的有…………………………………………………………………………………【 】
①相等的圆心角所对的弧相等;②平分弦的直径垂直于弦;③圆是轴对称图形,任何一条直径所在直线都是它的对称轴;④长度相等的两条弧是等弧.
A.3个 B.2个 C.1个 D.以上都不对
8.如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是直线x=1,下列结论正确的是………………………………………………………………………………………【 】
A.ac>0 B.2a﹣b=0 C.a﹣b+c=0 D.b2<4ac
9.如图,将一个装有水的杯子倾斜放置在水平桌面上,其截面可看作一个宽BC=6cm,长CD=16cm的矩形.当水面触到杯口边缘时,边CD恰有一半露出水面,那么此时水面高度是……………………【 】
A.9.6cm B.9.3cm C.8.6cm D.7.2cm
10.已知点A(a,b),B(4,c)在直线y=﹣2x+k(k为常数,k≠0)上,则ab的最大值为2,则c的值为………………………………………………………………………………………………………【 】
A.4或12 B.﹣4或﹣12 C.±4 D.±12
二、填空题(本大题共4小题,每小题5分,满分20分)
11.若=,则的值为 .
12.如图,点A在半圆O上,BC是直径,,若AB=,则BC的长为 .
13.如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=(x>0)的图象与BC边交于点E,若时,则k= .
14.如图,正方形ABCD与正方形CEGF有公共顶点C,连接AC、AG、BE,BC=3,BE=2.
(1)线段AG= .
(2)若点E是平面内一动点,BG的最小值等于 .
我们周五一起做练习
班级: 姓名:
一、选择题(本大题共10小题,每小题4分,满分40分) 12345678910
二、填空题(本大题共4小题,每小题5分,满分20分) 11. . 12. . 13. . 14.(1) ;(2) .
三、解答题(本大题共2小题,每小题8分,满分16分) 15.计算:.
16.如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1). (1)在图中以点O为位似中心在原点的另一侧画出△ABC放大2倍后得到的△A1B1C1,并写出A1的坐标; (2)请在图中画出△ABC绕点O逆时针旋转90°后得到的△A2B2C2.
四、解答题(本大题共2小题,每小题8分,满分16分) 17.已知抛物线y=x2﹣4x+7与y=x交于A、B两点(A在B点左侧). (1)请求出y<y时x的取值范围; (2)求抛物线顶点C的坐标,并求△ABC面积.
18.已知,如图,AB∥DC,∠ABC+∠ADB=180°. (1)求证:△ABD∽△BDC; (2)若AE平分∠DAB,BF平分∠DBC,且BF=2AE,S△ABD=3,求S△BDC.
五、解答题(本大题共2小题,每小题10分,满分20分) 19.如图所示的拱桥,用表示桥拱. (1)若所在圆的圆心为O,EF是弦CD的垂直平分线,请你利用尺规作图,找出圆心O.(不写作法,但要保留作图痕迹) 若拱桥的跨度AB的长为16m,拱高(的中点到弦AB的距离)为4m,求拱桥的半径R.
20.如图,某大楼的顶部竖有一块广告牌CD,小明与同学们在山坡的坡脚A处测得广告牌底部D的仰角为53°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:,AB=10米,AE=21米.(测角器的高度忽略不计,结果精确到0.1米,参考数据:≈1.41,≈1.73,sin53°≈,cos53°≈,tan53°≈) (1)求点B距水平地面AE的高度; (2)求广告牌CD的高度.(结果精确到0.1米)
六、(本题满分12分) 21.如图,⊙O是△ABC的外接圆,AE平分△ABC的外角∠DAC,OM⊥AB,ON⊥AC,垂足分别是点M、N,且OM=ON. (1)求证:AE∥BC; (2)如图,延长ON交AE于E点,若OE=7,ON=1,求⊙O的半径长.
七、(本题满分12分) 22.某公司销售一种商品,成本为每件30元,经过市场调查发现,该商品的日销售量y(件)与销售单价x(元)是一次函数关系,其销售单价、日销售量的三组对应数值如下表: 销售单价x(元)406080日销售量y(件)806040
(1)求日销售量y(件)与销售单价x(元)的函数关系式; (2)求公司销售该商品获得的最大日利润; (3)销售一段时间以后,由于某种原因,该商品每件成本增加了10元,若物价部门规定该商品销售单价不能超过a元,在日销售量y(件)与销售单价x(元)保持(1)中函数关系不变的情况下,该商品的日销售最大利润是1500元,求a的值.
八、(本题满分14分) 23.(1)如图1,正方形ABCD中,点E,F分别是AD、AB边上,且BE⊥CF于点O, 求证:BE=CF. (2)如图2,在(1)的条件下,连接AO并延长交BC于点G,若点G为BC边中点, 求证:AO2=AF AB. (3)在(2)的条件下,求tan∠ABE的值.
同课章节目录
