湖北省枣阳市白水高中2014-2015学年高二5月月考试题数学文试题
文档属性
| 名称 | 湖北省枣阳市白水高中2014-2015学年高二5月月考试题数学文试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 233.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-09 00:00:00 | ||
图片预览




文档简介
绝密★启用前
枣阳市白水高中2014-2015学年高二下学期文科数学5月月考试题
考试范围:xxx;考试时间:100分钟;命题人:xxx
题号
一
二
三
总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
评卷人
得分
一、选择题(10小题,每小题5分,共50分)
1.已知函数的最大值为4,最小值为0,最小正周期为,直线是其图像的一条对称轴,则下列各式中符合条件的解析式是( )
A. B.
C. D.
2.阅读如图一所示的程序框图,输出的结果的值为( )
A、 B、
C、 D、
3.已知等差数列中,,前9项和( )
A.108 B.72 C.36 D.18
4.已知集合,,则( )
A. B. C. D.
5.集合A={x|-1≤x≤2},B={x|x<1},则A∩(?RB)= ( )
A.{x|x>1} B.{x|x≥1} C.{x|16.已知为等差数列,若,则的值为 ( )
A. B. C.- D.
7.函数是奇函数,则等于
A.k (kZ) B.k+(kZ) C.k+(kZ) D.k-(kZ)
8.在Rt△ABC中,∠C=90°,且∠A,∠B,∠C所对的边a,b,c满足a+b=cx,则实数x的取值范围是( )
A.(0,1] B.(0,2] C.(1,2] D.(1,2)
9.函数f(x)=则该函数为( )
(A)单调递增函数,奇函数
(B)单调递增函数,偶函数
(C)单调递减函数,奇函数
(D)单调递减函数,偶函数
10.若复数 (a∈R,i是虚数单位)是纯虚数,则a的值为( )
A.-2 B.2 C.1 D.-1
评卷人
得分
二、填空题(5小题,每小题5分,共25分)
11.下列程序是求一个函数的函数值的程序:
INPUT x
IF x<=0 THEN y=-x
ELSE IF x>0 AND x<=1 THEN y=0
ELSE y=x-1
END IF
END IF
PRINT y
END
若执行的结果为3,则输入的x值为 .
12.在数列中,,则数列中的最大项是第 项。
13.在中,角A,B,C所对的边分别为a,b,c,若,,,则角A的大小为
14.若椭圆的左、右焦点分别为,线段被抛物线的焦点分成5﹕3的两段,则此椭圆的离心率为 .
15.从圆外一点向这个圆作两条切线,则这两条切线夹 角的余弦值为________________.
评卷人
得分
三、解答题(题型注释)
16.(本小题满分14分:6+8)
某投资公司投资甲、乙两个项目所得的利润分别是P(亿元)和Q(亿元),它们与投资额t(亿元)的关系有经验公式,今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所得的总利润为y(亿元)
(1)求y关于x的函数表达式;
(2)求总利润的最大值。
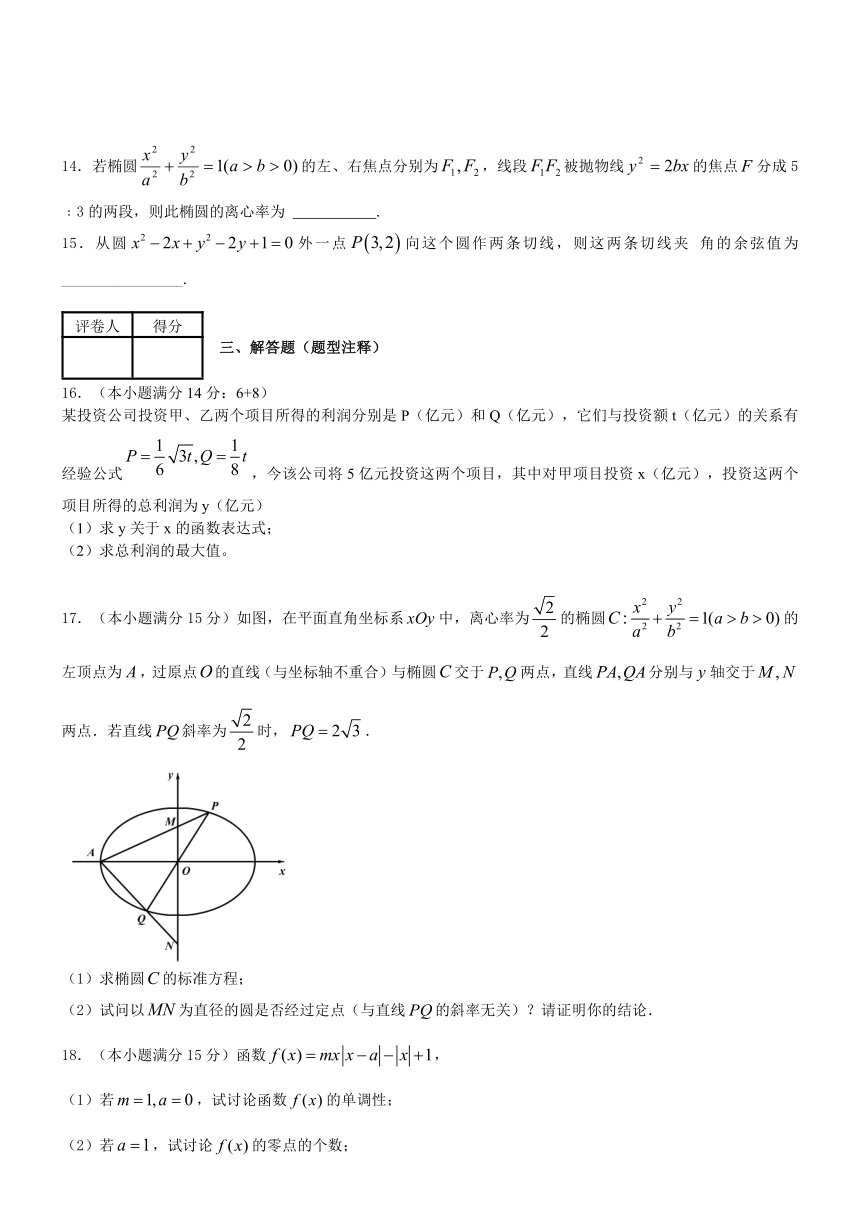
17.(本小题满分15分)如图,在平面直角坐标系中,离心率为的椭圆的左顶点为,过原点的直线(与坐标轴不重合)与椭圆交于两点,直线分别与轴交于两点.若直线斜率为时,.
(1)求椭圆的标准方程;
(2)试问以为直径的圆是否经过定点(与直线的斜率无关)?请证明你的结论.
18.(本小题满分15分)函数,
(1)若,试讨论函数的单调性;
(2)若,试讨论的零点的个数;
19.(本小题满分15分)在四棱锥中,底面为直角梯形,,侧面底面,,.
(1)若中点为.求证:;
(2)若,求直线与平面所成角的正弦值.
20.(本小题满分15分)已知的面积为,且.
(1)求;
(2)求求周长的最大值.
参考答案
1.D
【解析】
试题分析:由题意可得,则据此可知答案选D.
考点:函数的图像与性质.
2.A
【解析】根据程序框图可得,输出的
故选A
3.C
【解析】
试题分析:先由等差数列的性质,通过a5=4,求得a1+a9,再用求和公式求解.前9项和,故选C.
考点:等差数列的性质和前n项和公式
点评:本题主要考查等差数列的性质和前n项和公式,在高考中考查这一点比较多,应用性质不仅灵活,而且还将通项问题转化为前n项和,体现了两者间的内在联系,是常考常新的问题
4.D
【解析】解:因为=,=,因此选D
5.D
【解析】.故选D
6.C
【解析】解:
7.D
【解析】略
8.C
【解析】略
9.A
【解析】当x>0时,-x<0,则f(-x)=5-x-1=-f(x);当x<0时,-x>0,则f(-x)=1-5x=-f(x),又f(0)=0,所以函数f(x)为奇函数,易知函数在(0,+∞)递增,故函数在定义域内递增.故选A.
10.B
【解析】=,由已知可得a=2
11. -3或4
【解析】若,此时,解得,符合;
若,此时,不符合;
若,此时,解得,符合。
综上可得,或
12.6 或7
【解析】
试题分析:,所以数列前六项为单调递增,从第七项开始为单调递减,又,所以数列中的最大项是第6或7项。
考点:数列的单调性。
点评:我们经常利用作差法或者做商法来判断数列的单调性。但要注意用做商法时,数列的每一项都应是正的。
13.
【解析】略
14.
【解析】略
15.
【解析】略
16.
【解析】
(6分)
,
即(8分)
17.(1);(2)过定点.
【解析】
试题分析:(1)设椭圆的方程,若焦点明确,设椭圆的标准方程,结合条件用待定系数法求出的值,若不明确,需分焦点在轴和轴上两种情况讨论;(2)解决直线和椭圆的综合问题时注意:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与椭圆的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式:计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论.
试题解析:(1)设,
∵直线斜率为时,,∴,∴
∴,∵,∴.
∴椭圆的标准方程为.
(2)以为直径的圆过定点.
设,则,且,即,
∵,∴直线方程为: ,∴ ,
直线方程为: ,∴,
以为直径的圆为
即,
∵,∴,
令,,解得,
∴过定点:.
考点:1、椭圆的标准方程;2、直线与椭圆的综合问题.
18.(1)在和上为增函数,在上为减函数;(2)当时,函数有且仅有一个零点;
当或或或时,函数有两个零点;
当或时,有三个零点.
【解析】
试题分析:把代入函数,根据绝对值不等式的几何意义去掉绝对值的符号,根据函数的解析式作出函数的图象,根据函数图象讨论函数的单调性;(2)把函数的零点转化为方程的根,作图和的图象,直线移动过程中注意在什么范围内有一个零点,在什么范围内有两个零点,三个零点,通过数形结合解决有关问题.
试题解析:(1)
图像如下:
所以在和上为增函数,在上为减函数;
(2)的零点,除了零点以外的零点
即方程的根
作图和,如图可知:
当直线的斜率:
当时有一根;
当时有两根;
当时,有一根;
当时,有一根;
当(当和相切时)没有实数根;
当(当和相切时)有一根;
当时有两根.
综上所述:
当时,函数有且仅有一个零点;
当或或或时,函数有两个零点;
当或时,有三个零点.
考点:1、函数的单调性;2、函数零点的个数.
19.(1)证明见解析;(2).
【解析】
试题分析:(1)解决立体几何的有关问题,空间想象能力是非常重要的,但新旧知识的迁移融合也很重要,在平面几何的基础上,把某些空间问题转化为平面问题来解决,有时很方便;(2)证明线面平行常用方法:一是利用线面平行的判定定理,二是利用面面平行的性质定理,三是利用面面平行的性质;(3)证明线面垂直的方法:一是线面垂直的判定定理;二是利用面面垂直的性质定理;三是平行线法(若两条平行线中的一条垂直于这个平面,则另一条也垂直于这个平面.解题时,注意线线、线面与面面关系的相互转化;(4)在求三棱柱体积时,选择适当的底作为底面,这样体积容易计算.
试题解析:(1)取的中点,连结,
由于分别是的中点,,
又由于,
,且,所以为平行四边形.
,且不在平面内,在平面内,
所以
(2)等体积法
令点到平面的距离为
,
又
直线与平面所成角的正弦值.
考点:1、直线与平面平行的判定;2、直线与平面所成的角.
20.(1);(2).
【解析】
试题分析:(1)在三角形中处理边角关系时,一般全部转化为角的关系,或全部转化为边的关系.题中若出现边的一次式一般采用正弦定理,出现边的二次式一般采用余弦定理,应用正弦、余弦定理时,注意公式变形的应用,解决三角形问题时,注意角的限制范围;(2)在三角形中,注意隐含条件;(3)解决三角形问题时,根据边角关系灵活的选用定理和公式;(4)平方关系和商数关系式中的角都是同一个角,且商数关系式中;利用平方关系解决问题时,要注意开方运算结果的符号,需要根据角的范围确定.
试题解析:(1)∵△的面积为,且,∴,
∴,∴为锐角,且,
∴,所以.
(2)
所以周长为
==
,所以,,所以
所以周长最大值为.
考点:1、三角形的面积公式;2、正弦定理的应用;3、三角形的周长.
枣阳市白水高中2014-2015学年高二下学期文科数学5月月考试题
考试范围:xxx;考试时间:100分钟;命题人:xxx
题号
一
二
三
总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
评卷人
得分
一、选择题(10小题,每小题5分,共50分)
1.已知函数的最大值为4,最小值为0,最小正周期为,直线是其图像的一条对称轴,则下列各式中符合条件的解析式是( )
A. B.
C. D.
2.阅读如图一所示的程序框图,输出的结果的值为( )
A、 B、
C、 D、
3.已知等差数列中,,前9项和( )
A.108 B.72 C.36 D.18
4.已知集合,,则( )
A. B. C. D.
5.集合A={x|-1≤x≤2},B={x|x<1},则A∩(?RB)= ( )
A.{x|x>1} B.{x|x≥1} C.{x|1
A. B. C.- D.
7.函数是奇函数,则等于
A.k (kZ) B.k+(kZ) C.k+(kZ) D.k-(kZ)
8.在Rt△ABC中,∠C=90°,且∠A,∠B,∠C所对的边a,b,c满足a+b=cx,则实数x的取值范围是( )
A.(0,1] B.(0,2] C.(1,2] D.(1,2)
9.函数f(x)=则该函数为( )
(A)单调递增函数,奇函数
(B)单调递增函数,偶函数
(C)单调递减函数,奇函数
(D)单调递减函数,偶函数
10.若复数 (a∈R,i是虚数单位)是纯虚数,则a的值为( )
A.-2 B.2 C.1 D.-1
评卷人
得分
二、填空题(5小题,每小题5分,共25分)
11.下列程序是求一个函数的函数值的程序:
INPUT x
IF x<=0 THEN y=-x
ELSE IF x>0 AND x<=1 THEN y=0
ELSE y=x-1
END IF
END IF
PRINT y
END
若执行的结果为3,则输入的x值为 .
12.在数列中,,则数列中的最大项是第 项。
13.在中,角A,B,C所对的边分别为a,b,c,若,,,则角A的大小为
14.若椭圆的左、右焦点分别为,线段被抛物线的焦点分成5﹕3的两段,则此椭圆的离心率为 .
15.从圆外一点向这个圆作两条切线,则这两条切线夹 角的余弦值为________________.
评卷人
得分
三、解答题(题型注释)
16.(本小题满分14分:6+8)
某投资公司投资甲、乙两个项目所得的利润分别是P(亿元)和Q(亿元),它们与投资额t(亿元)的关系有经验公式,今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所得的总利润为y(亿元)
(1)求y关于x的函数表达式;
(2)求总利润的最大值。
17.(本小题满分15分)如图,在平面直角坐标系中,离心率为的椭圆的左顶点为,过原点的直线(与坐标轴不重合)与椭圆交于两点,直线分别与轴交于两点.若直线斜率为时,.
(1)求椭圆的标准方程;
(2)试问以为直径的圆是否经过定点(与直线的斜率无关)?请证明你的结论.
18.(本小题满分15分)函数,
(1)若,试讨论函数的单调性;
(2)若,试讨论的零点的个数;
19.(本小题满分15分)在四棱锥中,底面为直角梯形,,侧面底面,,.
(1)若中点为.求证:;
(2)若,求直线与平面所成角的正弦值.
20.(本小题满分15分)已知的面积为,且.
(1)求;
(2)求求周长的最大值.
参考答案
1.D
【解析】
试题分析:由题意可得,则据此可知答案选D.
考点:函数的图像与性质.
2.A
【解析】根据程序框图可得,输出的
故选A
3.C
【解析】
试题分析:先由等差数列的性质,通过a5=4,求得a1+a9,再用求和公式求解.前9项和,故选C.
考点:等差数列的性质和前n项和公式
点评:本题主要考查等差数列的性质和前n项和公式,在高考中考查这一点比较多,应用性质不仅灵活,而且还将通项问题转化为前n项和,体现了两者间的内在联系,是常考常新的问题
4.D
【解析】解:因为=,=,因此选D
5.D
【解析】.故选D
6.C
【解析】解:
7.D
【解析】略
8.C
【解析】略
9.A
【解析】当x>0时,-x<0,则f(-x)=5-x-1=-f(x);当x<0时,-x>0,则f(-x)=1-5x=-f(x),又f(0)=0,所以函数f(x)为奇函数,易知函数在(0,+∞)递增,故函数在定义域内递增.故选A.
10.B
【解析】=,由已知可得a=2
11. -3或4
【解析】若,此时,解得,符合;
若,此时,不符合;
若,此时,解得,符合。
综上可得,或
12.6 或7
【解析】
试题分析:,所以数列前六项为单调递增,从第七项开始为单调递减,又,所以数列中的最大项是第6或7项。
考点:数列的单调性。
点评:我们经常利用作差法或者做商法来判断数列的单调性。但要注意用做商法时,数列的每一项都应是正的。
13.
【解析】略
14.
【解析】略
15.
【解析】略
16.
【解析】
(6分)
,
即(8分)
17.(1);(2)过定点.
【解析】
试题分析:(1)设椭圆的方程,若焦点明确,设椭圆的标准方程,结合条件用待定系数法求出的值,若不明确,需分焦点在轴和轴上两种情况讨论;(2)解决直线和椭圆的综合问题时注意:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与椭圆的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式:计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论.
试题解析:(1)设,
∵直线斜率为时,,∴,∴
∴,∵,∴.
∴椭圆的标准方程为.
(2)以为直径的圆过定点.
设,则,且,即,
∵,∴直线方程为: ,∴ ,
直线方程为: ,∴,
以为直径的圆为
即,
∵,∴,
令,,解得,
∴过定点:.
考点:1、椭圆的标准方程;2、直线与椭圆的综合问题.
18.(1)在和上为增函数,在上为减函数;(2)当时,函数有且仅有一个零点;
当或或或时,函数有两个零点;
当或时,有三个零点.
【解析】
试题分析:把代入函数,根据绝对值不等式的几何意义去掉绝对值的符号,根据函数的解析式作出函数的图象,根据函数图象讨论函数的单调性;(2)把函数的零点转化为方程的根,作图和的图象,直线移动过程中注意在什么范围内有一个零点,在什么范围内有两个零点,三个零点,通过数形结合解决有关问题.
试题解析:(1)
图像如下:
所以在和上为增函数,在上为减函数;
(2)的零点,除了零点以外的零点
即方程的根
作图和,如图可知:
当直线的斜率:
当时有一根;
当时有两根;
当时,有一根;
当时,有一根;
当(当和相切时)没有实数根;
当(当和相切时)有一根;
当时有两根.
综上所述:
当时,函数有且仅有一个零点;
当或或或时,函数有两个零点;
当或时,有三个零点.
考点:1、函数的单调性;2、函数零点的个数.
19.(1)证明见解析;(2).
【解析】
试题分析:(1)解决立体几何的有关问题,空间想象能力是非常重要的,但新旧知识的迁移融合也很重要,在平面几何的基础上,把某些空间问题转化为平面问题来解决,有时很方便;(2)证明线面平行常用方法:一是利用线面平行的判定定理,二是利用面面平行的性质定理,三是利用面面平行的性质;(3)证明线面垂直的方法:一是线面垂直的判定定理;二是利用面面垂直的性质定理;三是平行线法(若两条平行线中的一条垂直于这个平面,则另一条也垂直于这个平面.解题时,注意线线、线面与面面关系的相互转化;(4)在求三棱柱体积时,选择适当的底作为底面,这样体积容易计算.
试题解析:(1)取的中点,连结,
由于分别是的中点,,
又由于,
,且,所以为平行四边形.
,且不在平面内,在平面内,
所以
(2)等体积法
令点到平面的距离为
,
又
直线与平面所成角的正弦值.
考点:1、直线与平面平行的判定;2、直线与平面所成的角.
20.(1);(2).
【解析】
试题分析:(1)在三角形中处理边角关系时,一般全部转化为角的关系,或全部转化为边的关系.题中若出现边的一次式一般采用正弦定理,出现边的二次式一般采用余弦定理,应用正弦、余弦定理时,注意公式变形的应用,解决三角形问题时,注意角的限制范围;(2)在三角形中,注意隐含条件;(3)解决三角形问题时,根据边角关系灵活的选用定理和公式;(4)平方关系和商数关系式中的角都是同一个角,且商数关系式中;利用平方关系解决问题时,要注意开方运算结果的符号,需要根据角的范围确定.
试题解析:(1)∵△的面积为,且,∴,
∴,∴为锐角,且,
∴,所以.
(2)
所以周长为
==
,所以,,所以
所以周长最大值为.
考点:1、三角形的面积公式;2、正弦定理的应用;3、三角形的周长.
