2023~2024学年中考数学之圆动点问题(线圆最值)(含解析)
文档属性
| 名称 | 2023~2024学年中考数学之圆动点问题(线圆最值)(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 856.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-11 20:28:24 | ||
图片预览




文档简介
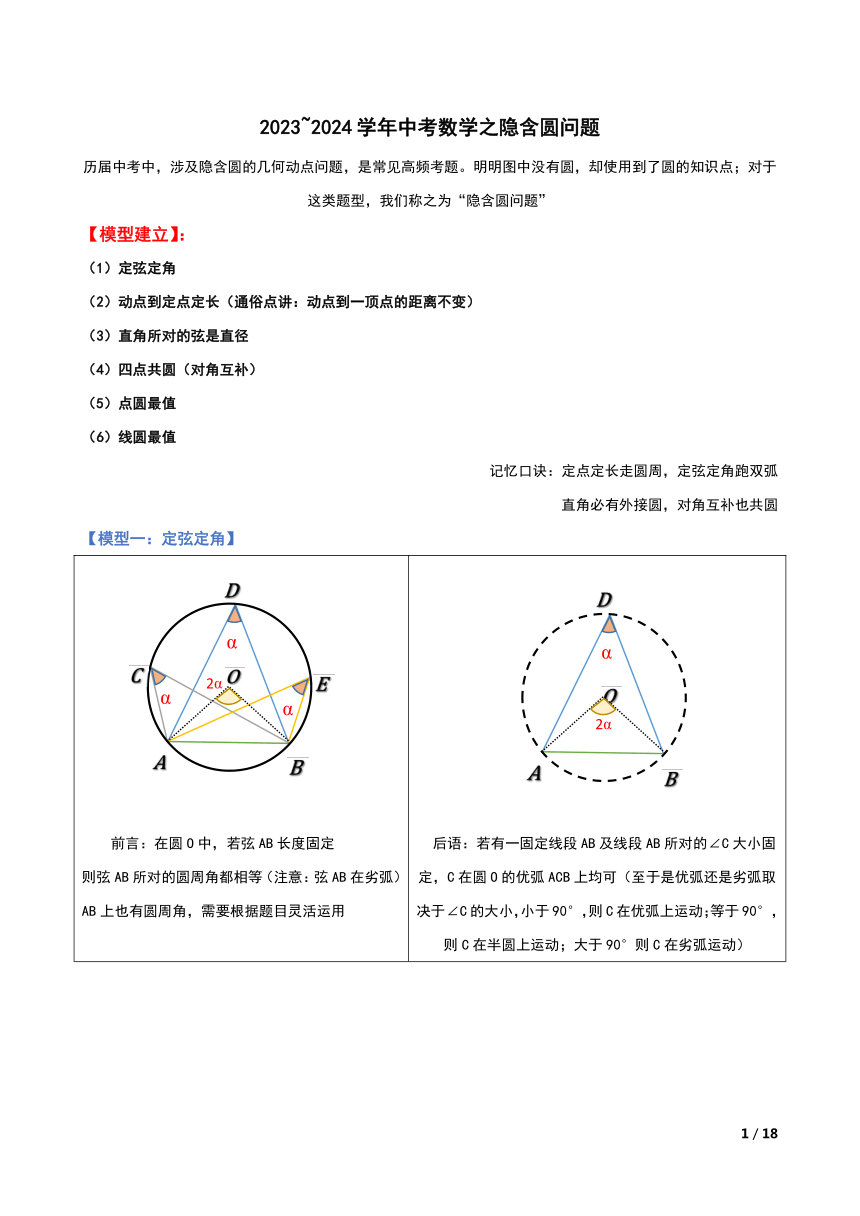
2023~2024学年中考数学之隐含圆问题
历届中考中,涉及隐含圆的几何动点问题,是常见高频考题。明明图中没有圆,却使用到了圆的知识点;对于这类题型,我们称之为“隐含圆问题”
【模型建立】:
(1)定弦定角
(2)动点到定点定长(通俗点讲:动点到一顶点的距离不变)
(3)直角所对的弦是直径
(4)四点共圆(对角互补)
(5)点圆最值
(6)线圆最值
记忆口诀:定点定长走圆周,定弦定角跑双弧
直角必有外接圆,对角互补也共圆
【模型一:定弦定角】
前言:在圆O中,若弦AB长度固定 则弦AB所对的圆周角都相等(注意:弦AB在劣弧)AB上也有圆周角,需要根据题目灵活运用 后语:若有一固定线段AB及线段AB所对的∠C大小固定,C在圆O的优弧ACB上均可(至于是优弧还是劣弧取决于∠C的大小,小于90°,则C在优弧上运动;等于90°,则C在半圆上运动;大于90°则C在劣弧运动)
1.(2023·凤岗模拟)如图,在正方形ABCD中,AB=4,E是对角线BD的中点,点F为BC所在直线上方一点,连接BF、CF、EF,若∠BFC=30°,则EF长的最大值为 .
【答案】2+2
【解析】【解答】解:作△BFC的外接圆,圆心为O,连接OF,OB,OC,过点O作OH⊥BC交于点H,如图所示:
∵四边形ABCD是正方形,
∴BC=AB=4,∠ABC=90°,,
∵∠BFC=30°,
∴∠BOC=2∠BFC=60°,
∴△BOC是等边三角形,
∴OB=OC=BC=4,
当点F是过点E的直径的端点时,EF取最大值,此时,OE⊥BC于点H.
又∵OE⊥BC,
∵BH=2,∠BOH=30°,
∴.
∵∠EBC=45°,∠EHB=90°,
∴△BHE是等腰直角三角形,
∴HE=BH=2,
∴,
故答案为:
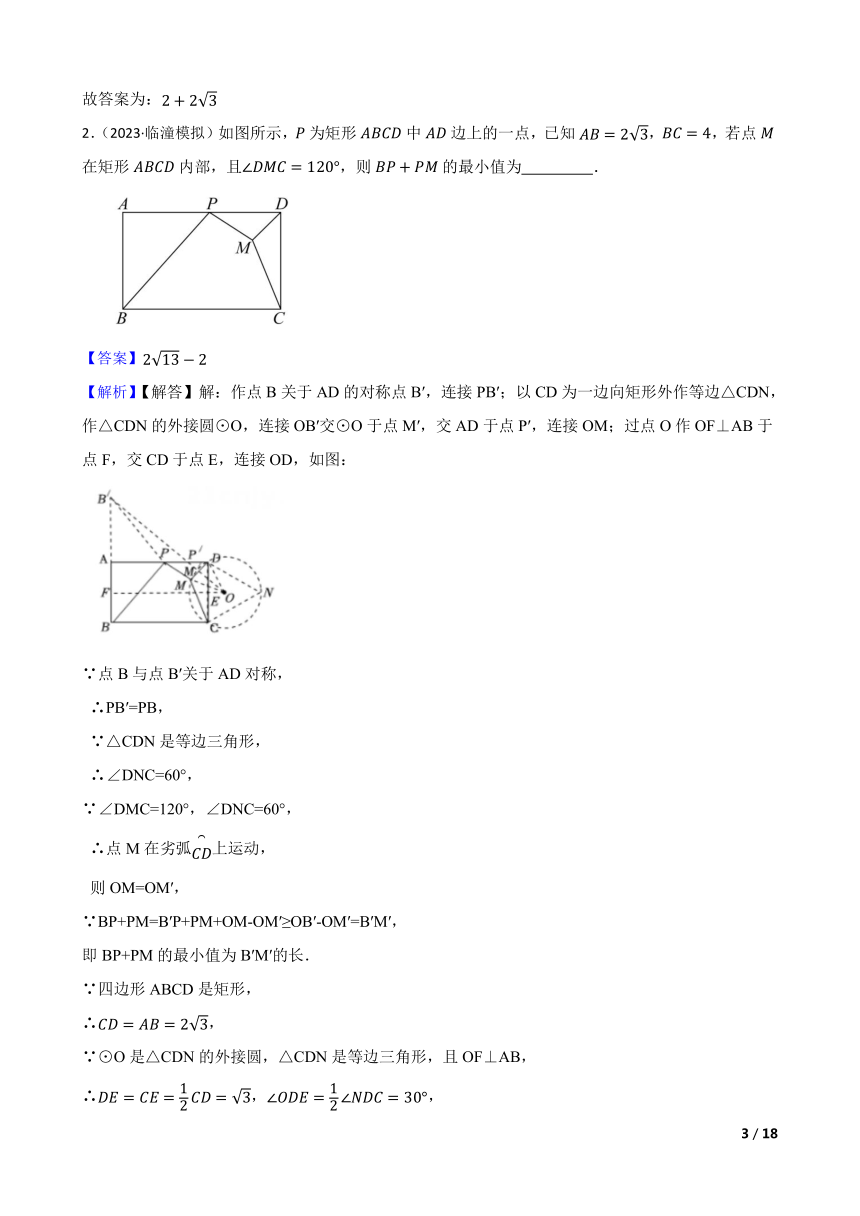
2.(2023·临潼模拟)如图所示,为矩形中边上的一点,已知,,若点在矩形内部,且,则的最小值为 .
【答案】
【解析】【解答】解:作点B关于AD的对称点B′,连接PB′;以CD为一边向矩形外作等边△CDN,作△CDN的外接圆⊙O,连接OB′交⊙O于点M′,交AD于点P′,连接OM;过点O作OF⊥AB于点F,交CD于点E,连接OD,如图:
∵点B与点B′关于AD对称,
∴PB′=PB,
∵△CDN是等边三角形,
∴∠DNC=60°,
∵∠DMC=120°,∠DNC=60°,
∴点M在劣弧上运动,
则OM=OM′,
∵BP+PM=B′P+PM+OM-OM′≥OB′-OM′=B′M′,
即BP+PM的最小值为B′M′的长.
∵四边形ABCD是矩形,
∴,
∵⊙O是△CDN的外接圆,△CDN是等边三角形,且OF⊥AB,
∴,,
∴OD=2OE,
在Rt△DOE中,OD2=DE2+OE2,
即,
解得:OE=1,
∴OD=2;
在Rt△OFB′中,
∵OF=EF+OE=BC+OE=4+1=5,
,
∴,
∴,
即BP+PM的最小值为,
故答案为:.
3.(2021·安徽模拟)如图,直角 中, ,AC=8, ,点 是 内部一动点,总满足∠APC=150°,连接 ,则 的最小值为( )
A. B. C. D.
【答案】B
【解析】【解答】解:如图,作△APC的外接圆⊙O,连接OA,OC,OB,OP,过点O作OH⊥BC交BC的延长线于H.
∵∠APC=150°,
∴∠AOC=60°,
∵OA=OC,
∴△AOC是等边三角形,
∴AC=OC=OA=OP=8,∠ACO=60°
在Rt△COH中,∠OCH=90°-60°=30°,
∴OH= OC=4,CH= OH= ,
∵BC= ,
∴BH= ,
∴OB= ,
∵PB≥OB-OP,
∴BP≥ ,
∴BP的最小值为 ,
故答案为:B.
4.(2023·惠山模拟)如图,抛物线与x轴交于点.
(1)求抛物线的函数表达式;
(2)点是抛物线上一点,点C是线段上一点,连接并延长交抛物线于点D,若,求点D的坐标;
(3)抛物线上是否存在点P,使得?若存在,求出点P的坐标:若不存在,说明理由.
【答案】(1)解:把点A的坐标代入函数解析式中, ,
解得: ,
故所求的解析式为 ;
(2)解:∵点B在抛物线 ,
∴ ,
即 ;
设直线 解析式为为 ,
则有 ,
解得: ,
∴直线 解析式为为 ;
过点C、D作x轴的垂线,垂足分别为E、F,如图,
设 ,则 ;
∵ ,
∴ ,
∴ ,
则 ,
∴ ;
∵点D在抛物线 上,
∴ ,
解得: ,
则点D的坐标为 ;
(3)解:存在;
如图,作 的外接圆 ,连接 ,过M作 轴于N,
∴ ,
∴ 是等腰直角三角形, 垂直平分 ,
∴ ,
∴M的坐标为 , 的半径 ;
设点P的坐标为 ,
则 ,
即 ,
由于 ,
∴方程整理得: ,
解得: ,
点P的坐标为 或 .
【模型二:动点到定点定长】
前言:在圆O中,OA=OB=OC=OD 后语:若有AB=AC=AD,则B、C、D三点在以A为圆心,AB为半径的圆上。 【理论依据:“到定点的距离等于定长的点的集合叫做圆“—圆的定义】
【模型三:直角所对的是直径】
前言:在圆O中,AB为直径,则始终有AB所对的∠C=90° 后语:若有AB是固定线段,且总有∠ACB=90°,则C在以AB为直径的圆上。(此类型本来属于定弦定角,但考频较高,且较为特殊故单独归为一类)
(2023九上·期末)如图,在Rt△ABC中,AB⊥BC,AB=6,BC=4.P是△ABC内部的一个动点,且满足∠PAB=∠PBC ,则线段CP长的最小值为
1.【答案】2
【解析】【解答】解:如图所示,以AB为直径作圆,圆心为O,连接OP、PC,当O、P、C三点共线时,OC最短..
∵AB=6,
∴圆O的半径等于3.
∵AB⊥AC,
∴∠ABP+∠PBC=90°.
∵∠PAB=∠PBC,
∴∠PAB+∠ABP=90°.
∴∠APB=180°-90°=90°.
∵OP恒为3,∴此时CP最短.
在Rt△ABC中,OC===5.
∴CP=5-3=2.
∴CP的长的最小值为2.
故答案为:2
2.(2023八下·芜湖期末)如图,正方形中,,E为边上一动点,连接,过点B作于F,连接,则的最小值为 .
【答案】2
【解析】【解答】
以BC中点O为圆心,BO的长为半径作圆,连接AO,交圆于点F,连接CF并延长交AB于点E,连接BF,则BF⊥CE.
由AO-FO≥AF可知,此时AO-FO=AF的值最小,∵AB=AD=4,∴FO=BO=2,∴AO=,∴AF的最小值为AO-FO=.
【模型四:四点共圆】
前言:在圆O中,ABCD是圆的内接四边形,则有∠1=∠2,∠3=∠4,△BPC∽△APD(同理△BPA∽△CPD) 后语:若四边形ABCD中有∠1=∠2(通常情况下∠5=∠6对顶角相等,故不需要∠3=∠4,实际应用中常用∠1=∠2,∠5=∠6)则ABCD四点(某些不能直接使用四点共圆的地区,可以通过证明两次三角形相似也可),选填题可以直接使用
1.(2022·东平模拟)如图,在矩形ABCD中,E、F分别在BC、CD上运动(不与端点重合),连接BF、AE,交于点P,且满足.连接CP,若AB=4,BC=6,则CP的最小值为 ( )
A.2-3 B.2-2 C.5 D.3
【答案】B
【解析】【解答】解:∵四边形ABCD是矩形,
∴AD=BC,∠BCF=∠ABE=90°,又,
∴,
∴△BCF∽△ABE,
∴∠BAE=∠FBC,又∠BAE+∠BEA=90°,
∴∠BEA+∠FBC=90°,
∴∠BPA=90°,
∴点P在以AB为直径的圆周上,设G为AB中点,连接CG,与圆G交于P,
即此时CP最短,
∴BG=2,
∴CG==,
∴此时CP=,
故答案为:B.
【分析】先证出点P在以AB为直径的圆周上,设G为AB中点,连接CG,与圆G交于P,即此时CP最短,再利用勾股定理求出CG的长,最后求出CP=即可。
【模型五:点圆最值】
平面内一定点D和圆O上动点E的连线中,当连线过圆心O时,线段DE的最大值和最小值,具体如以下三种情况,分类讨论(规定:OD=d,圆的半径为r)
(1)当D点在圆O外时,d>r,如图①② ;当D、E、O三点共线时,线段DE出现最值.DE的最大值为d+r,DE的最小值为d-r;
(2)当D点在圆O上时,d=r,如图③④ ;当D、E、O三点共线时,线段DE出现最值.DE的最大值为d+r=2r(即圆O直径),DE的最小值为d-r=0;
3)当D点在圆O内时,d<r,如图⑤⑥ ;当D、E、O三点共线时,线段DE出现最值.DE的最大值为d+r,DE的最小值为r-d;
1.(2023·徐汇模拟)如图,在直角坐标系中,已知点、点,的半径为5,点C是上的动点,点P是线段的中点,那么长的取值范围是 .
【答案】
【解析】【解答】解:∵A(8,0),点B(0,6),
∴OA= 8,OB=6,∠AOB = 90°,
连接AB,AC,取AB的中点D,则D的坐标(4,3);连接DP,
∵DP分别是AB、BC的中点,
∴DP= AC = x5=,
∴点D是定点,DP=,
即点P的运动轨迹是以点D为中心,DP为半径的圆,
∵DP1=DP2=,
∴点D坐标(4,3),
∴OP的取值范围是OD-DP1 ≤ OP≤OD+DP2,
即,
故答案为:.
【分析】根据题意先求出OA= 8,OB=6,∠AOB = 90°,再求出点D是定点,DP=,最后计算求解即可。
【模型六:线圆最值】
【1】(点圆距离)圆外一点P,连接PQ与圆交于A、B两点,则PA为P到圆上最远距离,PB为P到圆上最短距离。
【3】如图,AB为圆O的一条定弦,点C为圆上一动点。 如图①.若点C在优弧AB上,当CH⊥AB且CH过圆心O时,线段CH即为点C到弦AB的最大距离,此时S_△ABC的面积最大。 (2)如图②,若点C在劣弧AB上,当CH⊥AB且CH的延长线过圆心O时,线段CH即为点C到弦AB的最大距离,此时S_△ABC的面积最大。
1.(2022九上·莲都期中)如图,抛物线y=x2-4与x轴交于A、B两点,P是以点C(0,3)为圆心,2为半径的圆上的动点,Q是线段PA的中点,连接OQ,则线段OQ的最大值是( )
A.3 B. C. D.4
【答案】C
【知识点】二次函数的最值;二次函数图象与坐标轴的交点问题;点与圆的位置关系;三角形的中位线定理;圆-动点问题
【解析】【解答】解:连接BP,如图,
当y=0时,x2-4=0,解得x1=4,x2=-4,则A(-4,0),B(4,0),
∵Q是线段PA的中点,
∴OQ为△ABP的中位线,
∴OQ=BP,
当BP最大时,OQ最大,
而BP过圆心C时,PB最大,如图,点P运动到P′位置时,BP最大,
∵BC==5,
∴BP′=5+2=7,
∴线段OQ的最大值是.
故答案为:C.
2.(2023·东平模拟)如图,在矩形纸片ABCD中,,,点E是AB的中点,点F是AD边上的一个动点,将沿EF所在直线翻折,得到,则的长的最小值是
B.3 C. D.
【答案】D
【解析】【解答】以点E为圆心,AE长度为半径作圆,连接CE,当点在线段CE上时,的长取最小值,如图所示,
根据折叠可知:.
在中,,,,
,
的最小值.
故答案为:D.
3.(2023·天河模拟)如图,矩形中,,,点、分别是线段,上的动点,且,过作的垂线,垂足为.
(1)当时,
(2)当在上运动时,的最小值为 .
【答案】(1)45
(2)1
【知识点】矩形的判定与性质;圆的综合题;锐角三角函数的定义;三角形全等的判定(ASA)
【解析】【解答】解:(1)过点F作FM⊥BC于M,如图,
则∠BME=∠EMF= 90°,
∵四边形ABCD为矩形,
∴∠A=∠B= 90°,
∴四边形ABME是矩形,
∴EM=AB=2,BM=AE=,
∵AE = CF,
∴CF=BM=,
∵AE = CF,
∴CF=BM=,
∴MF=BC-BM-CF=,
∴ME = MF,
∵FM⊥BC,
∴∠BFE= 45°,
故答案为:45°;
(2)连接BD交EF于点O,如图,
由矩形性质知:AD∥CB,AD= BC=, AE= CF,
∴∠DEF=∠BFE,AD- AE= BC- CF,
∴DE= BF,
∴∠EOD =∠FOB,
∴△DOE≌△BOF (ASA),
∴ OD=OB,
由勾股定理得,
∴OD=2,BD=4,
∵DH⊥EF,设OD的中点为M,
∴MH=1,
即点H在以点M为圆心,以1为半径的圆上运动,
由于点E在AD边上运动,
∴当点E与点A重合时,即EF与AC重合时,CH的值最小,
∵AC= BD= 4,
,
即CH的最小值为1;
故答案为:1.
【分析】(1)过点F作FM⊥BC于M,由条件可得四边形ABME是矩形,由题意可得MF= EM,从而问题解决;
(2)连接BD交EF于点O,可证明△DOE≌△BOF,易得OD = 12,BD= 2,由DH⊥EF知,MH = 2,即点H在以OD中点M为圆心,1为半径的圆上运动,当点E与点A重合时,CH的值最小,由三角函数知识即可求得此时最小值.
1 / 1
历届中考中,涉及隐含圆的几何动点问题,是常见高频考题。明明图中没有圆,却使用到了圆的知识点;对于这类题型,我们称之为“隐含圆问题”
【模型建立】:
(1)定弦定角
(2)动点到定点定长(通俗点讲:动点到一顶点的距离不变)
(3)直角所对的弦是直径
(4)四点共圆(对角互补)
(5)点圆最值
(6)线圆最值
记忆口诀:定点定长走圆周,定弦定角跑双弧
直角必有外接圆,对角互补也共圆
【模型一:定弦定角】
前言:在圆O中,若弦AB长度固定 则弦AB所对的圆周角都相等(注意:弦AB在劣弧)AB上也有圆周角,需要根据题目灵活运用 后语:若有一固定线段AB及线段AB所对的∠C大小固定,C在圆O的优弧ACB上均可(至于是优弧还是劣弧取决于∠C的大小,小于90°,则C在优弧上运动;等于90°,则C在半圆上运动;大于90°则C在劣弧运动)
1.(2023·凤岗模拟)如图,在正方形ABCD中,AB=4,E是对角线BD的中点,点F为BC所在直线上方一点,连接BF、CF、EF,若∠BFC=30°,则EF长的最大值为 .
【答案】2+2
【解析】【解答】解:作△BFC的外接圆,圆心为O,连接OF,OB,OC,过点O作OH⊥BC交于点H,如图所示:
∵四边形ABCD是正方形,
∴BC=AB=4,∠ABC=90°,,
∵∠BFC=30°,
∴∠BOC=2∠BFC=60°,
∴△BOC是等边三角形,
∴OB=OC=BC=4,
当点F是过点E的直径的端点时,EF取最大值,此时,OE⊥BC于点H.
又∵OE⊥BC,
∵BH=2,∠BOH=30°,
∴.
∵∠EBC=45°,∠EHB=90°,
∴△BHE是等腰直角三角形,
∴HE=BH=2,
∴,
故答案为:
2.(2023·临潼模拟)如图所示,为矩形中边上的一点,已知,,若点在矩形内部,且,则的最小值为 .
【答案】
【解析】【解答】解:作点B关于AD的对称点B′,连接PB′;以CD为一边向矩形外作等边△CDN,作△CDN的外接圆⊙O,连接OB′交⊙O于点M′,交AD于点P′,连接OM;过点O作OF⊥AB于点F,交CD于点E,连接OD,如图:
∵点B与点B′关于AD对称,
∴PB′=PB,
∵△CDN是等边三角形,
∴∠DNC=60°,
∵∠DMC=120°,∠DNC=60°,
∴点M在劣弧上运动,
则OM=OM′,
∵BP+PM=B′P+PM+OM-OM′≥OB′-OM′=B′M′,
即BP+PM的最小值为B′M′的长.
∵四边形ABCD是矩形,
∴,
∵⊙O是△CDN的外接圆,△CDN是等边三角形,且OF⊥AB,
∴,,
∴OD=2OE,
在Rt△DOE中,OD2=DE2+OE2,
即,
解得:OE=1,
∴OD=2;
在Rt△OFB′中,
∵OF=EF+OE=BC+OE=4+1=5,
,
∴,
∴,
即BP+PM的最小值为,
故答案为:.
3.(2021·安徽模拟)如图,直角 中, ,AC=8, ,点 是 内部一动点,总满足∠APC=150°,连接 ,则 的最小值为( )
A. B. C. D.
【答案】B
【解析】【解答】解:如图,作△APC的外接圆⊙O,连接OA,OC,OB,OP,过点O作OH⊥BC交BC的延长线于H.
∵∠APC=150°,
∴∠AOC=60°,
∵OA=OC,
∴△AOC是等边三角形,
∴AC=OC=OA=OP=8,∠ACO=60°
在Rt△COH中,∠OCH=90°-60°=30°,
∴OH= OC=4,CH= OH= ,
∵BC= ,
∴BH= ,
∴OB= ,
∵PB≥OB-OP,
∴BP≥ ,
∴BP的最小值为 ,
故答案为:B.
4.(2023·惠山模拟)如图,抛物线与x轴交于点.
(1)求抛物线的函数表达式;
(2)点是抛物线上一点,点C是线段上一点,连接并延长交抛物线于点D,若,求点D的坐标;
(3)抛物线上是否存在点P,使得?若存在,求出点P的坐标:若不存在,说明理由.
【答案】(1)解:把点A的坐标代入函数解析式中, ,
解得: ,
故所求的解析式为 ;
(2)解:∵点B在抛物线 ,
∴ ,
即 ;
设直线 解析式为为 ,
则有 ,
解得: ,
∴直线 解析式为为 ;
过点C、D作x轴的垂线,垂足分别为E、F,如图,
设 ,则 ;
∵ ,
∴ ,
∴ ,
则 ,
∴ ;
∵点D在抛物线 上,
∴ ,
解得: ,
则点D的坐标为 ;
(3)解:存在;
如图,作 的外接圆 ,连接 ,过M作 轴于N,
∴ ,
∴ 是等腰直角三角形, 垂直平分 ,
∴ ,
∴M的坐标为 , 的半径 ;
设点P的坐标为 ,
则 ,
即 ,
由于 ,
∴方程整理得: ,
解得: ,
点P的坐标为 或 .
【模型二:动点到定点定长】
前言:在圆O中,OA=OB=OC=OD 后语:若有AB=AC=AD,则B、C、D三点在以A为圆心,AB为半径的圆上。 【理论依据:“到定点的距离等于定长的点的集合叫做圆“—圆的定义】
【模型三:直角所对的是直径】
前言:在圆O中,AB为直径,则始终有AB所对的∠C=90° 后语:若有AB是固定线段,且总有∠ACB=90°,则C在以AB为直径的圆上。(此类型本来属于定弦定角,但考频较高,且较为特殊故单独归为一类)
(2023九上·期末)如图,在Rt△ABC中,AB⊥BC,AB=6,BC=4.P是△ABC内部的一个动点,且满足∠PAB=∠PBC ,则线段CP长的最小值为
1.【答案】2
【解析】【解答】解:如图所示,以AB为直径作圆,圆心为O,连接OP、PC,当O、P、C三点共线时,OC最短..
∵AB=6,
∴圆O的半径等于3.
∵AB⊥AC,
∴∠ABP+∠PBC=90°.
∵∠PAB=∠PBC,
∴∠PAB+∠ABP=90°.
∴∠APB=180°-90°=90°.
∵OP恒为3,∴此时CP最短.
在Rt△ABC中,OC===5.
∴CP=5-3=2.
∴CP的长的最小值为2.
故答案为:2
2.(2023八下·芜湖期末)如图,正方形中,,E为边上一动点,连接,过点B作于F,连接,则的最小值为 .
【答案】2
【解析】【解答】
以BC中点O为圆心,BO的长为半径作圆,连接AO,交圆于点F,连接CF并延长交AB于点E,连接BF,则BF⊥CE.
由AO-FO≥AF可知,此时AO-FO=AF的值最小,∵AB=AD=4,∴FO=BO=2,∴AO=,∴AF的最小值为AO-FO=.
【模型四:四点共圆】
前言:在圆O中,ABCD是圆的内接四边形,则有∠1=∠2,∠3=∠4,△BPC∽△APD(同理△BPA∽△CPD) 后语:若四边形ABCD中有∠1=∠2(通常情况下∠5=∠6对顶角相等,故不需要∠3=∠4,实际应用中常用∠1=∠2,∠5=∠6)则ABCD四点(某些不能直接使用四点共圆的地区,可以通过证明两次三角形相似也可),选填题可以直接使用
1.(2022·东平模拟)如图,在矩形ABCD中,E、F分别在BC、CD上运动(不与端点重合),连接BF、AE,交于点P,且满足.连接CP,若AB=4,BC=6,则CP的最小值为 ( )
A.2-3 B.2-2 C.5 D.3
【答案】B
【解析】【解答】解:∵四边形ABCD是矩形,
∴AD=BC,∠BCF=∠ABE=90°,又,
∴,
∴△BCF∽△ABE,
∴∠BAE=∠FBC,又∠BAE+∠BEA=90°,
∴∠BEA+∠FBC=90°,
∴∠BPA=90°,
∴点P在以AB为直径的圆周上,设G为AB中点,连接CG,与圆G交于P,
即此时CP最短,
∴BG=2,
∴CG==,
∴此时CP=,
故答案为:B.
【分析】先证出点P在以AB为直径的圆周上,设G为AB中点,连接CG,与圆G交于P,即此时CP最短,再利用勾股定理求出CG的长,最后求出CP=即可。
【模型五:点圆最值】
平面内一定点D和圆O上动点E的连线中,当连线过圆心O时,线段DE的最大值和最小值,具体如以下三种情况,分类讨论(规定:OD=d,圆的半径为r)
(1)当D点在圆O外时,d>r,如图①② ;当D、E、O三点共线时,线段DE出现最值.DE的最大值为d+r,DE的最小值为d-r;
(2)当D点在圆O上时,d=r,如图③④ ;当D、E、O三点共线时,线段DE出现最值.DE的最大值为d+r=2r(即圆O直径),DE的最小值为d-r=0;
3)当D点在圆O内时,d<r,如图⑤⑥ ;当D、E、O三点共线时,线段DE出现最值.DE的最大值为d+r,DE的最小值为r-d;
1.(2023·徐汇模拟)如图,在直角坐标系中,已知点、点,的半径为5,点C是上的动点,点P是线段的中点,那么长的取值范围是 .
【答案】
【解析】【解答】解:∵A(8,0),点B(0,6),
∴OA= 8,OB=6,∠AOB = 90°,
连接AB,AC,取AB的中点D,则D的坐标(4,3);连接DP,
∵DP分别是AB、BC的中点,
∴DP= AC = x5=,
∴点D是定点,DP=,
即点P的运动轨迹是以点D为中心,DP为半径的圆,
∵DP1=DP2=,
∴点D坐标(4,3),
∴OP的取值范围是OD-DP1 ≤ OP≤OD+DP2,
即,
故答案为:.
【分析】根据题意先求出OA= 8,OB=6,∠AOB = 90°,再求出点D是定点,DP=,最后计算求解即可。
【模型六:线圆最值】
【1】(点圆距离)圆外一点P,连接PQ与圆交于A、B两点,则PA为P到圆上最远距离,PB为P到圆上最短距离。
【3】如图,AB为圆O的一条定弦,点C为圆上一动点。 如图①.若点C在优弧AB上,当CH⊥AB且CH过圆心O时,线段CH即为点C到弦AB的最大距离,此时S_△ABC的面积最大。 (2)如图②,若点C在劣弧AB上,当CH⊥AB且CH的延长线过圆心O时,线段CH即为点C到弦AB的最大距离,此时S_△ABC的面积最大。
1.(2022九上·莲都期中)如图,抛物线y=x2-4与x轴交于A、B两点,P是以点C(0,3)为圆心,2为半径的圆上的动点,Q是线段PA的中点,连接OQ,则线段OQ的最大值是( )
A.3 B. C. D.4
【答案】C
【知识点】二次函数的最值;二次函数图象与坐标轴的交点问题;点与圆的位置关系;三角形的中位线定理;圆-动点问题
【解析】【解答】解:连接BP,如图,
当y=0时,x2-4=0,解得x1=4,x2=-4,则A(-4,0),B(4,0),
∵Q是线段PA的中点,
∴OQ为△ABP的中位线,
∴OQ=BP,
当BP最大时,OQ最大,
而BP过圆心C时,PB最大,如图,点P运动到P′位置时,BP最大,
∵BC==5,
∴BP′=5+2=7,
∴线段OQ的最大值是.
故答案为:C.
2.(2023·东平模拟)如图,在矩形纸片ABCD中,,,点E是AB的中点,点F是AD边上的一个动点,将沿EF所在直线翻折,得到,则的长的最小值是
B.3 C. D.
【答案】D
【解析】【解答】以点E为圆心,AE长度为半径作圆,连接CE,当点在线段CE上时,的长取最小值,如图所示,
根据折叠可知:.
在中,,,,
,
的最小值.
故答案为:D.
3.(2023·天河模拟)如图,矩形中,,,点、分别是线段,上的动点,且,过作的垂线,垂足为.
(1)当时,
(2)当在上运动时,的最小值为 .
【答案】(1)45
(2)1
【知识点】矩形的判定与性质;圆的综合题;锐角三角函数的定义;三角形全等的判定(ASA)
【解析】【解答】解:(1)过点F作FM⊥BC于M,如图,
则∠BME=∠EMF= 90°,
∵四边形ABCD为矩形,
∴∠A=∠B= 90°,
∴四边形ABME是矩形,
∴EM=AB=2,BM=AE=,
∵AE = CF,
∴CF=BM=,
∵AE = CF,
∴CF=BM=,
∴MF=BC-BM-CF=,
∴ME = MF,
∵FM⊥BC,
∴∠BFE= 45°,
故答案为:45°;
(2)连接BD交EF于点O,如图,
由矩形性质知:AD∥CB,AD= BC=, AE= CF,
∴∠DEF=∠BFE,AD- AE= BC- CF,
∴DE= BF,
∴∠EOD =∠FOB,
∴△DOE≌△BOF (ASA),
∴ OD=OB,
由勾股定理得,
∴OD=2,BD=4,
∵DH⊥EF,设OD的中点为M,
∴MH=1,
即点H在以点M为圆心,以1为半径的圆上运动,
由于点E在AD边上运动,
∴当点E与点A重合时,即EF与AC重合时,CH的值最小,
∵AC= BD= 4,
,
即CH的最小值为1;
故答案为:1.
【分析】(1)过点F作FM⊥BC于M,由条件可得四边形ABME是矩形,由题意可得MF= EM,从而问题解决;
(2)连接BD交EF于点O,可证明△DOE≌△BOF,易得OD = 12,BD= 2,由DH⊥EF知,MH = 2,即点H在以OD中点M为圆心,1为半径的圆上运动,当点E与点A重合时,CH的值最小,由三角函数知识即可求得此时最小值.
1 / 1
