湖北省枣阳市高级中学2014-2015学年高二5月月考数学理科试题
文档属性
| 名称 | 湖北省枣阳市高级中学2014-2015学年高二5月月考数学理科试题 |  | |
| 格式 | zip | ||
| 文件大小 | 202.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-09 20:11:39 | ||
图片预览




文档简介
绝密★启用前
枣阳市高级中学2014-2015学年高二下学期理科数学5月月考试题
考试范围:xxx;考试时间:100分钟;命题人:xxx
题号
一
二
三
总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
评卷人
得分
一、选择题(10小题,每小题5分,共50分)
1.设集合A={x|x∈Z且-10≤x≤-1},B={x|x∈Z,且|x|≤5},则A∪B中的元素个数是
A.11 B.10 C.16 D.15
2.已知三棱锥P-ABC中,底面ABC是边长为2的正三角形,平面ABC,且PA=1,
则点A到平面PBC的距离为( )
A.1 B. C. D.
3.在中,若,则角B为( )
A. B. C. D.
4.集合A={(x,y)|y=a},集合B={(x,y)|y=+1,b>0,b≠1},若集合A∩B,则实数a的取值范围是 ( )
A.(-∞,1) B.(-∞,1]
C.(1,+∞) D. [1,+∞)
5.函数的单调递增区间为( )
A.
B.
C.
D.
6. 某校高三年级有男生500人,女生400人,为了解该年级学生的健康情况,从男生中任意抽取25人,从女生中任意抽取20人进行调查.这种抽样方法是( )
(A)简单随机抽样法 (B)抽签法 (C)随机数表法 (D)分层抽样法
7.下列函数中,最小值为2的是( )
A. B.
C. y= sinx+,x(0,) D.
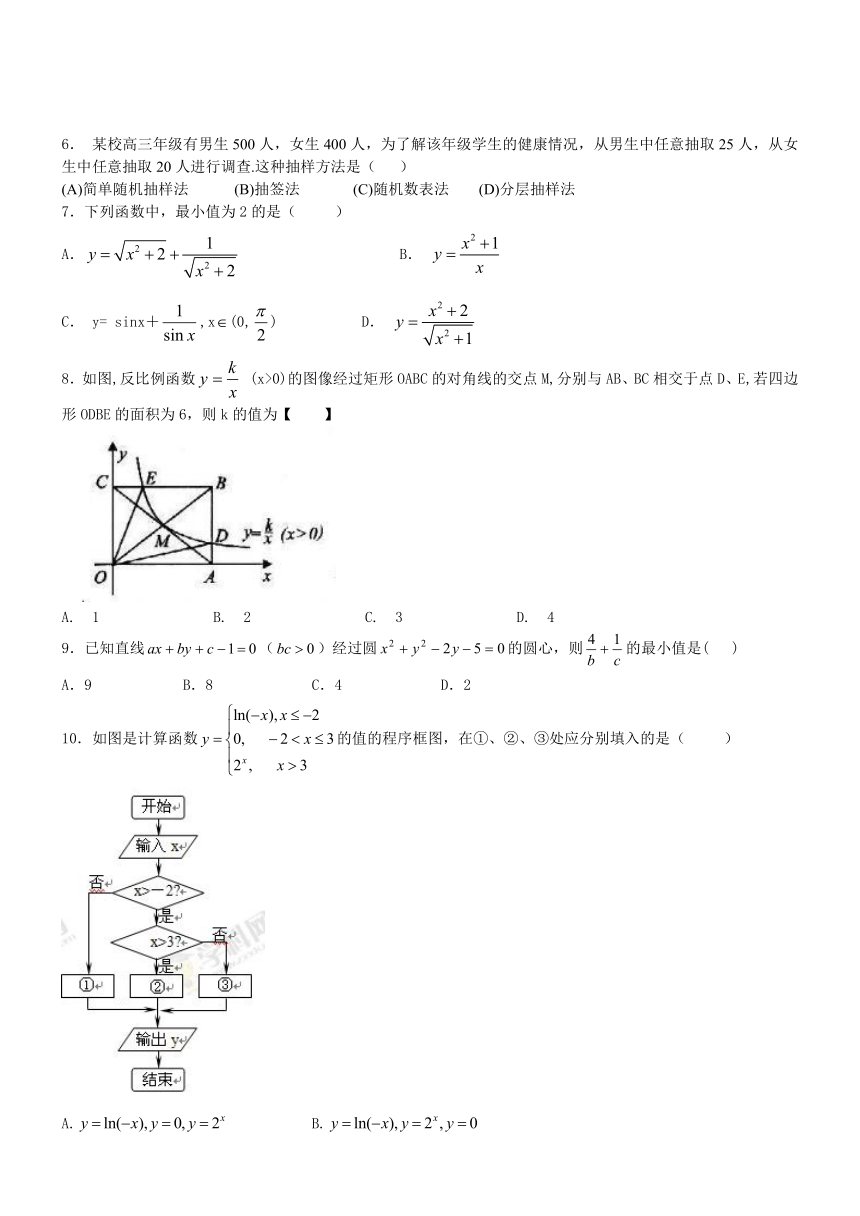
8.如图,反比例函数 (x>0)的图像经过矩形OABC的对角线的交点M,分别与AB、BC相交于点D、E,若四边形ODBE的面积为6,则k的值为【 】
A. 1 B. 2 C. 3 D. 4
9.已知直线()经过圆的圆心,则的最小值是( )
A.9 B.8 C.4 D.2
10.如图是计算函数的值的程序框图,在①、②、③处应分别填入的是( )
A. B.
C. D.
评卷人
得分
二、填空题(5小题,每小题5分,共25分)
11. 抛物线的焦点坐标是
12.在三张奖券中有一、二等奖各一张,另一张无奖,甲乙两人各抽取一张(不放回),两人都中奖的概率为
13.已知函数在处的切线经过原点,则函数的极小值为 ▲
14.函数的定义域是 .
15.在曲线y=-+2x-1的所有切线中,斜率为正整数的切线有_______条.
评卷人
得分
三、解答题(题型注释)
16.某射手有5发子弹,射击一次命中概率为0.9,如果命中就停止射击,否则一直到子弹用尽,求耗用子弹数的分布列.
17.平面直角坐标系中有一个△ABC,角A,B,C所对应的边分别为,已知坐标原点与顶点B重合,且,,=,且∠A为锐角。(12分)
(1)求角A的大小;
(2)若,求实数的取值范围;
(3)若,顶点A,,求△ABC的面积。
18.(本小题12分)
已知集合,,请画出从集合到集合的所有函数关系,并写出每种函数关系中的定义域及值域.
19.(本小题满分12分)
古代印度婆罗门教寺庙内的僧侣们曾经玩过一种被称为“河内宝塔问题”的游戏,其玩法如下:如图,设有n()个圆盘依其半径大小,大的在下,小的在上套在A柱上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子A、B、C可供使用.
现用an表示将n个圆盘全部从A柱上移到C柱上所至少需要移动的次数,回答下列问题:
写出a1,a2,a3,并求出an;
记,求和();
(其中表示所有的积的和)
证明:.
20.(本小题满分14分)为了保护环境,某工厂在国家的号召下,把废弃物回收转化为某种产品,经测算,处理成本(万元)与处理量(吨)之间的函数关系可近似的表示为:,
(1)当处理量为多少吨时,每吨的平均处理成本最少?
(2)若每处理一吨废弃物可得价值为万元的某种产品,同时获得国家补贴万元.当时,判断该项举措能否获利?如果能获利,求出最大利润;如果不能获利,请求出国家最少补贴多少万元,该工厂才不会亏损?
21.(本题满分12分)设的定义域为,且在是递增的,
(1)求证:;
(2)设,解不等式.
22.已知一企业生产某产品的年固定成本为10万元,每生产千件需另投入2.7万元,设该企业年内共生产此种产品千件,并且全部销售完,每千件的销售收入为万元,且
(1)写出年利润(万元)关于年产品(千件)的函数解析式;
(2)年产量为多少千件时,该企业生产此产品所获年利润最大?
(注:年利润=年销售收入-年总成本)
参考答案
1.C
【解析】
试题分析:因为,A={x|x∈Z且-10≤x≤-1}={-10,-9,-8,-7,-6,-5,-4,-3,-2,-1},
B={x|x∈Z,且|x|≤5}={-5,-4,-3,-2,-2,-1,0,1,2,3,4,5},
A∪B={-10,-9,-8,-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5}其中共16个元素
考点:本题主要考查集合的运算,简单不等式解法。
点评:简单题,并集是由两集合中的所有元素构成的集合。也可按公式计算。
2.C
【解析】平面ABC,所以,
在等腰中,BC边上的高等于
是正三角形,,,设则点A到平面PBC的距离为h;
则由得:
故选C
3.B
【解析】因为,所以.
4.C
【解析】函数的值域为,因为集合A∩B,所以,故选择C
5.C
【解析】
试题分析:由于函数的单调递增区间为,而是向左平移了个单位得到的,所以的单调递增区间为
考点:1,正切函数的单调性 2,三角函数图象的变换
6.D
【解析】略
7.D
【解析】解:因为选项A,c中利用均值不等式时等号不能取到,因此达不到最小值2,而选项B中,x的正负不定因此不能确定有最下值,选项D中,当且仅当x=0时取等号。
8.B
【解析】
试题分析:
本题可从反比例函数图象上的点E、M、D入手,分别找出△OCE、△OAD、□OABC的面积与|k|的关系,列出等式求出k值。解:由题意得:E、M、D位于反比例函数图象上,则S△OCE=,S△OAD=,过点M作MG⊥y轴于点G,作MN⊥x轴于点N,则S□ONMG=|k|,又∵M为矩形ABCO对角线的交点,则S矩形ABCO=4S□ONMG=4|k|,
由于函数图象在第一象限,k>0,则++6=4k,k=2.故选B.
考点:反比例函数
点评:本试题考查了反比例系数k的几何意义,过双曲线上任意一点向两条坐标轴作垂线,与坐标轴围城的矩形的面积等于|k|,属于基础题。
9.A
【解析】
试题分析:由圆的一般方程,知,所以,圆心的坐标为
又因为直线()经过该圆心.所以,即
所以,
因为,所以,所以,
当且仅当,即时,取“=”号.故选
考点:1、基本不等式;2、圆的方程.
10.B
【解析】
试题分析:①处应填入自变量的解析式,②处应填入自变量的解析式,③处应填入自变量的解析式。
考点:算法程序框图。
11.(0, )
【解析】抛物线的标准方程为,焦点坐标为(0, )。
12.
【解析】
试题分析:甲乙两人各抽取一张(不放回)共有6种基本事件,其中两人都中奖包含两种基本事件,所以概率为
考点:古典概型概率
13.-5
【解析】解:
故过点(1,-a)的切线方程为y+a=(3-2a)(x-1),过原点,所以a=3,
,在(0,2)递减,在(-,0)和(2,+)递增,因此在x=2处取得极小值,且为-5
14.
【解析】
试题分析:由定义域的求法知,函数的定义域为,解得.
考点:函数定义域的求法.
15.
【解析】
试题分析:因为,在曲线y=-+2x-1的所有切线中,斜率为正整数的有,所以斜率为时,切线为,当斜率为时,有两条切线,故共有条斜率为正整数的切线.
考点:导数的几何意义.
16.见解析
【解析】本题要求我们给出耗用子弹数的概率分布列.我们知道只有5发子弹,所以的取值只有1,2,3,4,5.当时,即;当时,要求第一次没射中,第二次射中,故;同理,时,要求前两次没有射中,第三次射中,;类似地,;第5次射击不同,只要前四次射不中,都要射第5发子弹,也不考虑是否射中,所以,所以耗用子弹数的分布列为:
0
1
2
3
0.9
0.09
0.009
0.0001
17.(1)(2)-1≤m<(3)
【解析】
试题分析:⑴ =, ∴,
∴或, ∴或.
又∵角A是锐角,∴.
⑵ ==,
∵0<<, ∴<<, ∴-<≤1, ∴-1≤m<.
⑶∵ ,∴,
又,∴,∴.
考点:本小题主要考查三角函数的化简和求值,正弦定理.
点评:化简三角函数式时,要灵活运用三角函数公式,三角函数中公式众多,要灵活选择,更要注意公式的适用条件.
18.定义域: 定义域: 定义域: 定义域:
值 域: 值 域: 值 域: 值 域:
【解析】本试题主要是考查而来集合与函数的关系的运用。必须满足集合A中的所有的元素,在集合B中有唯一的像即可,那么可知符合题意的有4种情况。
解:(每个3分,共12分)
定义域: 定义域: 定义域: 定义域:
值 域: 值 域: 值 域: 值 域:
19.(1)(2)(3)略
【解析】(1)
事实上,要将个圆盘全部转移到C柱上,只需先将上面个圆盘转移到B柱上,需要次转移,然后将最大的那个圆盘转移到C柱上,需要一次转移,再将柱上的个圆盘转移到C柱上,需要次转移,所以有
则,所以
(2)
则
()
(3) 令,则当时
又,所以对一切有:
另方面恒成立,所以对一切有
综上所述有:
20.(1),(2)能获利,当处理量为吨时,最大利润为225万元.
【解析】
试题分析:(1)根据平均的定义可列函数关系式:平均处理成本为,然后根据基本不等式求其最值: , 当且仅当时等号成立,由 得.(2)利润为产值加补贴减去成本,即
,.这是二次函数,利用对称轴与定义区间位置关系,可判定其处理量为吨时,最大利润为225万元.
试题解析:解:(1)设平均处理成本为
2分
, 4分
当且仅当时等号成立,由 得.
因此,当处理量为吨时,每吨的处理成本最少为万元. 6分.
(2)根据题意得,利润和处理量之间的关系:
8分
,.
∵,在上为增函数, 10分
可求得. 12分
∴能获利,当处理量为吨时,最大利润为225万元. 14分
考点:基本不等式求最值,二次函数求最值
21.(1)详见解析;(2)
【解析】
试题分析:(1)赋值法.令代入条件式,得;;(2)有条件式可得,又,由(1)可知,再由函数为定义域上的增函数,去掉函数符号,列不等式组解得即可.
试题解析:(1)证明:,令,则有:, 2分
4分
(2)解:∵,
∵,
等价于: 8分
由定义域为可得 10分
又在上为增函数,
又
∴原不等式解集为: 12分
考点:(1)赋值法求函数值;(2)抽象函数中单调性的应用.
22.(1)(2)9
【解析】
试题分析:利用基本不等式解决实际问题时,应先仔细阅读题目信息,理解题意,明确其中的数量关系,并引入变量,依题意列出相应的函数关系式,然后利用基本不等式求解;(2)在求所列函数的最值时,若用基本不等式时,等号取不到时,可利用函数的单调性求解;(3)基本不等式具有将“和式”转化为“积式”和将“积式”转化为“和式”的放缩功能,常常用于比较数的大小或证明不等式,解决问题的关键是分析不等式两边的结构特点,选择好利用基本不等式的切入点.
试题解析:(1)当时,
当时,
(2)①当时,由,得,
当时,;当时,;
当时,取最大值,且
② 当时,
当且仅当,即时,
综合①、②知时,取最大值.
所以当年产量为9千件时,该企业生产此产品获利最大.
考点:函数及其性质的应用.
枣阳市高级中学2014-2015学年高二下学期理科数学5月月考试题
考试范围:xxx;考试时间:100分钟;命题人:xxx
题号
一
二
三
总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
评卷人
得分
一、选择题(10小题,每小题5分,共50分)
1.设集合A={x|x∈Z且-10≤x≤-1},B={x|x∈Z,且|x|≤5},则A∪B中的元素个数是
A.11 B.10 C.16 D.15
2.已知三棱锥P-ABC中,底面ABC是边长为2的正三角形,平面ABC,且PA=1,
则点A到平面PBC的距离为( )
A.1 B. C. D.
3.在中,若,则角B为( )
A. B. C. D.
4.集合A={(x,y)|y=a},集合B={(x,y)|y=+1,b>0,b≠1},若集合A∩B,则实数a的取值范围是 ( )
A.(-∞,1) B.(-∞,1]
C.(1,+∞) D. [1,+∞)
5.函数的单调递增区间为( )
A.
B.
C.
D.
6. 某校高三年级有男生500人,女生400人,为了解该年级学生的健康情况,从男生中任意抽取25人,从女生中任意抽取20人进行调查.这种抽样方法是( )
(A)简单随机抽样法 (B)抽签法 (C)随机数表法 (D)分层抽样法
7.下列函数中,最小值为2的是( )
A. B.
C. y= sinx+,x(0,) D.
8.如图,反比例函数 (x>0)的图像经过矩形OABC的对角线的交点M,分别与AB、BC相交于点D、E,若四边形ODBE的面积为6,则k的值为【 】
A. 1 B. 2 C. 3 D. 4
9.已知直线()经过圆的圆心,则的最小值是( )
A.9 B.8 C.4 D.2
10.如图是计算函数的值的程序框图,在①、②、③处应分别填入的是( )
A. B.
C. D.
评卷人
得分
二、填空题(5小题,每小题5分,共25分)
11. 抛物线的焦点坐标是
12.在三张奖券中有一、二等奖各一张,另一张无奖,甲乙两人各抽取一张(不放回),两人都中奖的概率为
13.已知函数在处的切线经过原点,则函数的极小值为 ▲
14.函数的定义域是 .
15.在曲线y=-+2x-1的所有切线中,斜率为正整数的切线有_______条.
评卷人
得分
三、解答题(题型注释)
16.某射手有5发子弹,射击一次命中概率为0.9,如果命中就停止射击,否则一直到子弹用尽,求耗用子弹数的分布列.
17.平面直角坐标系中有一个△ABC,角A,B,C所对应的边分别为,已知坐标原点与顶点B重合,且,,=,且∠A为锐角。(12分)
(1)求角A的大小;
(2)若,求实数的取值范围;
(3)若,顶点A,,求△ABC的面积。
18.(本小题12分)
已知集合,,请画出从集合到集合的所有函数关系,并写出每种函数关系中的定义域及值域.
19.(本小题满分12分)
古代印度婆罗门教寺庙内的僧侣们曾经玩过一种被称为“河内宝塔问题”的游戏,其玩法如下:如图,设有n()个圆盘依其半径大小,大的在下,小的在上套在A柱上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子A、B、C可供使用.
现用an表示将n个圆盘全部从A柱上移到C柱上所至少需要移动的次数,回答下列问题:
写出a1,a2,a3,并求出an;
记,求和();
(其中表示所有的积的和)
证明:.
20.(本小题满分14分)为了保护环境,某工厂在国家的号召下,把废弃物回收转化为某种产品,经测算,处理成本(万元)与处理量(吨)之间的函数关系可近似的表示为:,
(1)当处理量为多少吨时,每吨的平均处理成本最少?
(2)若每处理一吨废弃物可得价值为万元的某种产品,同时获得国家补贴万元.当时,判断该项举措能否获利?如果能获利,求出最大利润;如果不能获利,请求出国家最少补贴多少万元,该工厂才不会亏损?
21.(本题满分12分)设的定义域为,且在是递增的,
(1)求证:;
(2)设,解不等式.
22.已知一企业生产某产品的年固定成本为10万元,每生产千件需另投入2.7万元,设该企业年内共生产此种产品千件,并且全部销售完,每千件的销售收入为万元,且
(1)写出年利润(万元)关于年产品(千件)的函数解析式;
(2)年产量为多少千件时,该企业生产此产品所获年利润最大?
(注:年利润=年销售收入-年总成本)
参考答案
1.C
【解析】
试题分析:因为,A={x|x∈Z且-10≤x≤-1}={-10,-9,-8,-7,-6,-5,-4,-3,-2,-1},
B={x|x∈Z,且|x|≤5}={-5,-4,-3,-2,-2,-1,0,1,2,3,4,5},
A∪B={-10,-9,-8,-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5}其中共16个元素
考点:本题主要考查集合的运算,简单不等式解法。
点评:简单题,并集是由两集合中的所有元素构成的集合。也可按公式计算。
2.C
【解析】平面ABC,所以,
在等腰中,BC边上的高等于
是正三角形,,,设则点A到平面PBC的距离为h;
则由得:
故选C
3.B
【解析】因为,所以.
4.C
【解析】函数的值域为,因为集合A∩B,所以,故选择C
5.C
【解析】
试题分析:由于函数的单调递增区间为,而是向左平移了个单位得到的,所以的单调递增区间为
考点:1,正切函数的单调性 2,三角函数图象的变换
6.D
【解析】略
7.D
【解析】解:因为选项A,c中利用均值不等式时等号不能取到,因此达不到最小值2,而选项B中,x的正负不定因此不能确定有最下值,选项D中,当且仅当x=0时取等号。
8.B
【解析】
试题分析:
本题可从反比例函数图象上的点E、M、D入手,分别找出△OCE、△OAD、□OABC的面积与|k|的关系,列出等式求出k值。解:由题意得:E、M、D位于反比例函数图象上,则S△OCE=,S△OAD=,过点M作MG⊥y轴于点G,作MN⊥x轴于点N,则S□ONMG=|k|,又∵M为矩形ABCO对角线的交点,则S矩形ABCO=4S□ONMG=4|k|,
由于函数图象在第一象限,k>0,则++6=4k,k=2.故选B.
考点:反比例函数
点评:本试题考查了反比例系数k的几何意义,过双曲线上任意一点向两条坐标轴作垂线,与坐标轴围城的矩形的面积等于|k|,属于基础题。
9.A
【解析】
试题分析:由圆的一般方程,知,所以,圆心的坐标为
又因为直线()经过该圆心.所以,即
所以,
因为,所以,所以,
当且仅当,即时,取“=”号.故选
考点:1、基本不等式;2、圆的方程.
10.B
【解析】
试题分析:①处应填入自变量的解析式,②处应填入自变量的解析式,③处应填入自变量的解析式。
考点:算法程序框图。
11.(0, )
【解析】抛物线的标准方程为,焦点坐标为(0, )。
12.
【解析】
试题分析:甲乙两人各抽取一张(不放回)共有6种基本事件,其中两人都中奖包含两种基本事件,所以概率为
考点:古典概型概率
13.-5
【解析】解:
故过点(1,-a)的切线方程为y+a=(3-2a)(x-1),过原点,所以a=3,
,在(0,2)递减,在(-,0)和(2,+)递增,因此在x=2处取得极小值,且为-5
14.
【解析】
试题分析:由定义域的求法知,函数的定义域为,解得.
考点:函数定义域的求法.
15.
【解析】
试题分析:因为,在曲线y=-+2x-1的所有切线中,斜率为正整数的有,所以斜率为时,切线为,当斜率为时,有两条切线,故共有条斜率为正整数的切线.
考点:导数的几何意义.
16.见解析
【解析】本题要求我们给出耗用子弹数的概率分布列.我们知道只有5发子弹,所以的取值只有1,2,3,4,5.当时,即;当时,要求第一次没射中,第二次射中,故;同理,时,要求前两次没有射中,第三次射中,;类似地,;第5次射击不同,只要前四次射不中,都要射第5发子弹,也不考虑是否射中,所以,所以耗用子弹数的分布列为:
0
1
2
3
0.9
0.09
0.009
0.0001
17.(1)(2)-1≤m<(3)
【解析】
试题分析:⑴ =, ∴,
∴或, ∴或.
又∵角A是锐角,∴.
⑵ ==,
∵0<<, ∴<<, ∴-<≤1, ∴-1≤m<.
⑶∵ ,∴,
又,∴,∴.
考点:本小题主要考查三角函数的化简和求值,正弦定理.
点评:化简三角函数式时,要灵活运用三角函数公式,三角函数中公式众多,要灵活选择,更要注意公式的适用条件.
18.定义域: 定义域: 定义域: 定义域:
值 域: 值 域: 值 域: 值 域:
【解析】本试题主要是考查而来集合与函数的关系的运用。必须满足集合A中的所有的元素,在集合B中有唯一的像即可,那么可知符合题意的有4种情况。
解:(每个3分,共12分)
定义域: 定义域: 定义域: 定义域:
值 域: 值 域: 值 域: 值 域:
19.(1)(2)(3)略
【解析】(1)
事实上,要将个圆盘全部转移到C柱上,只需先将上面个圆盘转移到B柱上,需要次转移,然后将最大的那个圆盘转移到C柱上,需要一次转移,再将柱上的个圆盘转移到C柱上,需要次转移,所以有
则,所以
(2)
则
()
(3) 令,则当时
又,所以对一切有:
另方面恒成立,所以对一切有
综上所述有:
20.(1),(2)能获利,当处理量为吨时,最大利润为225万元.
【解析】
试题分析:(1)根据平均的定义可列函数关系式:平均处理成本为,然后根据基本不等式求其最值: , 当且仅当时等号成立,由 得.(2)利润为产值加补贴减去成本,即
,.这是二次函数,利用对称轴与定义区间位置关系,可判定其处理量为吨时,最大利润为225万元.
试题解析:解:(1)设平均处理成本为
2分
, 4分
当且仅当时等号成立,由 得.
因此,当处理量为吨时,每吨的处理成本最少为万元. 6分.
(2)根据题意得,利润和处理量之间的关系:
8分
,.
∵,在上为增函数, 10分
可求得. 12分
∴能获利,当处理量为吨时,最大利润为225万元. 14分
考点:基本不等式求最值,二次函数求最值
21.(1)详见解析;(2)
【解析】
试题分析:(1)赋值法.令代入条件式,得;;(2)有条件式可得,又,由(1)可知,再由函数为定义域上的增函数,去掉函数符号,列不等式组解得即可.
试题解析:(1)证明:,令,则有:, 2分
4分
(2)解:∵,
∵,
等价于: 8分
由定义域为可得 10分
又在上为增函数,
又
∴原不等式解集为: 12分
考点:(1)赋值法求函数值;(2)抽象函数中单调性的应用.
22.(1)(2)9
【解析】
试题分析:利用基本不等式解决实际问题时,应先仔细阅读题目信息,理解题意,明确其中的数量关系,并引入变量,依题意列出相应的函数关系式,然后利用基本不等式求解;(2)在求所列函数的最值时,若用基本不等式时,等号取不到时,可利用函数的单调性求解;(3)基本不等式具有将“和式”转化为“积式”和将“积式”转化为“和式”的放缩功能,常常用于比较数的大小或证明不等式,解决问题的关键是分析不等式两边的结构特点,选择好利用基本不等式的切入点.
试题解析:(1)当时,
当时,
(2)①当时,由,得,
当时,;当时,;
当时,取最大值,且
② 当时,
当且仅当,即时,
综合①、②知时,取最大值.
所以当年产量为9千件时,该企业生产此产品获利最大.
考点:函数及其性质的应用.
