第5章练习卷(进阶篇)2023-2024学年下学期小学数学人教新版四年级单元测试(含答案)
文档属性
| 名称 | 第5章练习卷(进阶篇)2023-2024学年下学期小学数学人教新版四年级单元测试(含答案) |  | |
| 格式 | Doc | ||
| 文件大小 | 209.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-11 19:55:08 | ||
图片预览




文档简介
(进阶篇)2023-2024学年下学期小学数学人教新版四年级第5章练习卷
一.选择题(共5小题)
1.一个三角形的两条边分别是6厘米和7厘米,那么第三条边的长度最长是( )
A.13厘米 B.12厘米 C.10厘米 D.15厘米
2.一个三角尺上有( )个锐角。
A.1 B.2 C.3
3.在三角形三个内角中,∠1=∠2+∠3,那么这个三角形一定是( )三角形.
A.钝角 B.直角 C.锐角 D.等腰
4.一个三角形至少有( )个锐角.
A.1 B.2 C.3 D.无法确定
5.把一个等边三角形平均分成两个直角三角形,其中一个直角三角形的两个锐角分别是( )
A.30°和30° B.30°和60° C.60°和60°
二.填空题(共5小题)
6.等腰三角形的底角是35°,顶角是 。等边三角形的每个内角都是 。
7.直角三角形三个角的度数分别是60°、 和 。
8.一个三角形的两条边长分别是3分米、8分米,第三条边可能是 分米。(多选少选不得分)
A.5
B.9
C.12
D.6
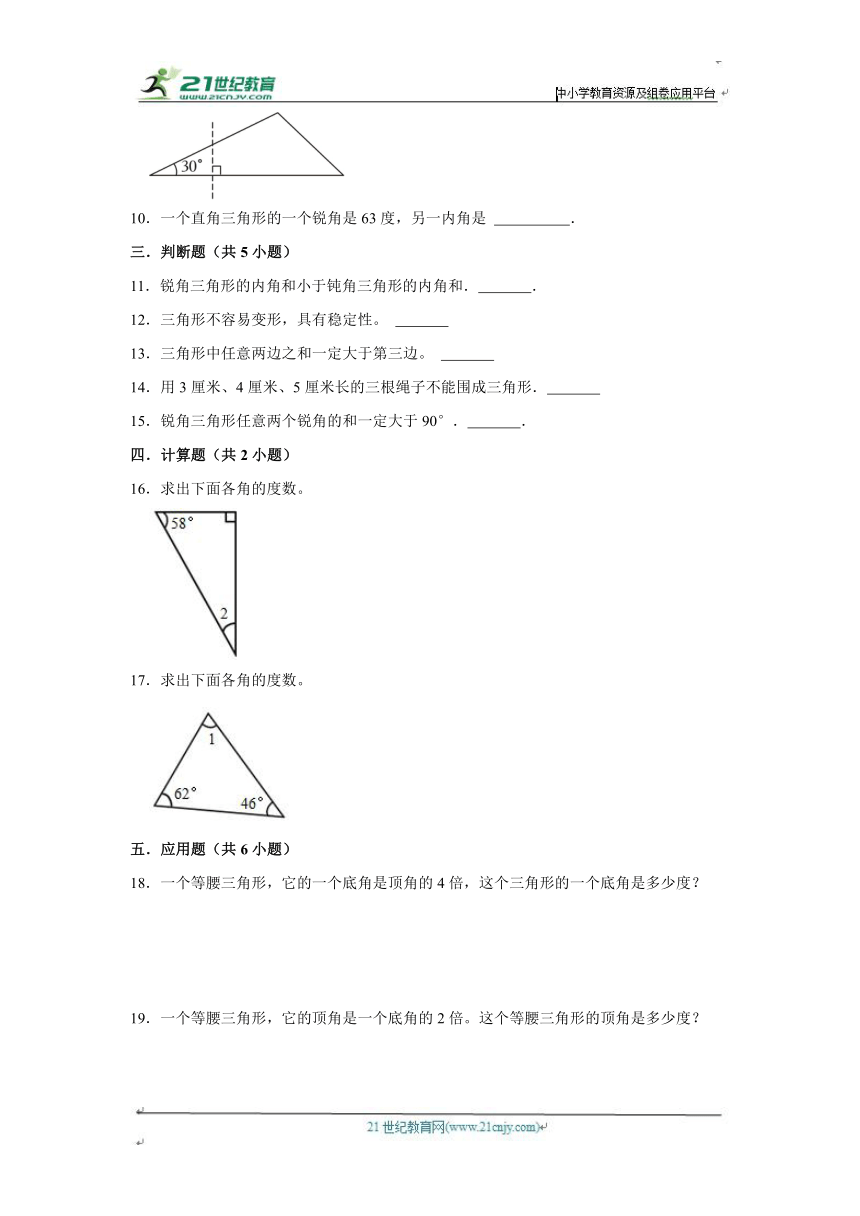
9.在一个三角形中,一个锐角是30°,截去这个角(如图所示),剩下图形的内角和是 °。
10.一个直角三角形的一个锐角是63度,另一内角是 .
三.判断题(共5小题)
11.锐角三角形的内角和小于钝角三角形的内角和. .
12.三角形不容易变形,具有稳定性。
13.三角形中任意两边之和一定大于第三边。
14.用3厘米、4厘米、5厘米长的三根绳子不能围成三角形.
15.锐角三角形任意两个锐角的和一定大于90°. .
四.计算题(共2小题)
16.求出下面各角的度数。
17.求出下面各角的度数。
五.应用题(共6小题)
18.一个等腰三角形,它的一个底角是顶角的4倍,这个三角形的一个底角是多少度?
19.一个等腰三角形,它的顶角是一个底角的2倍。这个等腰三角形的顶角是多少度?
20.如果一个三角形的三条边长度都是整厘米数,第一条边长度是5cm,第二条边的长度比6厘米长而且比10厘米短,第三边的长度最短是多少厘米?最长是多少厘米?
21.一个三角形中,∠A的度数是27.5°,∠B的度数是∠A的1.6倍,那么∠C是多少度?这是一个什么三角形?
22.李爷爷家有一块三角形的菜地,菜地的最大内角是120°,是最小角的四倍,这块三角形菜地其它两个角各是多少度?按边分,这是一个什么三角形菜地?
23.如果两个三角形3条边的长度分别相等,那么这两个三角形3个角的度数也分别相等吗?
六.操作题(共2小题)
24.在点子图上按要求画图。
25.求下面各角的度数.
(1)如图1,∠B=∠C=70度∠A=
(2)如图2,∠B是直角,∠C=65度,∠A= .
(进阶篇)2023-2024学年下学期小学数学人教新版四年级第5章练习卷
参考答案与试题解析
一.选择题(共5小题)
1.一个三角形的两条边分别是6厘米和7厘米,那么第三条边的长度最长是( )
A.13厘米 B.12厘米 C.10厘米 D.15厘米
【解答】解:7﹣6<第三边<7+6,
即1厘米<第三边<13厘米。
即第三边在1厘米~13厘米之间(不包括1厘米和13厘米)。
答:第三条边的长度最长是12厘米,最短是2厘米。
故选:B。
2.一个三角尺上有( )个锐角。
A.1 B.2 C.3
【解答】解:一个三角尺上有2个锐角。
故选:B。
3.在三角形三个内角中,∠1=∠2+∠3,那么这个三角形一定是( )三角形.
A.钝角 B.直角 C.锐角 D.等腰
【解答】解:由分析得:在三角形三个内角中,∠1=∠2+∠3,也就是180÷2=90(度),90÷2=45(度),那么这个三角形一定是直角三角形.
故选:B.
4.一个三角形至少有( )个锐角.
A.1 B.2 C.3 D.无法确定
【解答】解:假设三角形中锐角的个数少于2个,那么三角形中就会出现两个或两个以上的角是钝角或直角,
两个钝角或两个直角的和加上第三个角的度数一定大于180°,这就违背了三角形内角和是180°的性质,
所以一个三角形至少有2个锐角.
故选:B.
5.把一个等边三角形平均分成两个直角三角形,其中一个直角三角形的两个锐角分别是( )
A.30°和30° B.30°和60° C.60°和60°
【解答】解:60°÷2=30°
答:其中一个直角三角形的两个锐角分别是30°和60°。
故选:B。
二.填空题(共5小题)
6.等腰三角形的底角是35°,顶角是 110° 。等边三角形的每个内角都是 60° 。
【解答】解:180°﹣35°×2
=180°﹣70°
=110°
180°÷3=60°
答:等腰三角形的底角是35°,顶角是110°,等边三角形的每个内角都是60°。
故答案为:110°,60°。
7.直角三角形三个角的度数分别是60°、 90° 和 30° 。
【解答】解:180°﹣90°﹣60°=30°
答:如果是直角三角形,三个角分别是60o,90°,30°。
故答案为:90°,30°。
8.一个三角形的两条边长分别是3分米、8分米,第三条边可能是 B或D 分米。(多选少选不得分)
A.5
B.9
C.12
D.6
【解答】解:由三角形的特性可知:8分米﹣3分米<第三条边<3分米+8分米,
即5分米<第三条边<11分米,所以结合选项可知,第三条边可能是9分米或6分米。
故答案为:B或D。
9.在一个三角形中,一个锐角是30°,截去这个角(如图所示),剩下图形的内角和是 360 °。
【解答】解:剩下的图形可以分成两个三角形,所以剩下图形的内角和是180°×2=360°。
答:剩下图形的内角和是360°。
故答案为:360。
10.一个直角三角形的一个锐角是63度,另一内角是 27° .
【解答】解:直角三角形中有一个角是90°,
所以另一个锐角为90°﹣63°=27°,
答:另一个锐角是27°.
故答案为:27°.
三.判断题(共5小题)
11.锐角三角形的内角和小于钝角三角形的内角和. × .
【解答】解:因为任何三角形内角和都是180°,所以原题说法是错误的.
故答案为:×.
12.三角形不容易变形,具有稳定性。 √
【解答】解:例如:用一根钢条将一扇打开的玻璃窗支撑起来,这样风就不容易吹动窗户,这里所用的原理就是三角形的稳定性。如下图所示:
故答案为:√。
13.三角形中任意两边之和一定大于第三边。 √
【解答】解:三角形中任意两边之和一定大于第三边。原题说法正确。
故答案为:√。
14.用3厘米、4厘米、5厘米长的三根绳子不能围成三角形. ×
【解答】解:3+4>5
5﹣3<4
所以用3厘米、4厘米、5厘米的三根绳子能围成一个三角形,所以本题说法错误;
故答案为:×.
15.锐角三角形任意两个锐角的和一定大于90°. √ .
【解答】解:如果两个锐角和不大于90°,那么第三个角将大于等于90°,就不再是锐角三角形.
所以上面的说法是正确的.
故答案为:√.
四.计算题(共2小题)
16.求出下面各角的度数。
【解答】解:根据图示可知三角形为直角三角形,
∠2=180°﹣90°﹣58°=32°
17.求出下面各角的度数。
【解答】解:∠1=180°﹣62°﹣46°=72°
五.应用题(共6小题)
18.一个等腰三角形,它的一个底角是顶角的4倍,这个三角形的一个底角是多少度?
【解答】解:设顶角是x度,则底角就是4x度。
x+4x+4x=180°
9x=180°
9x÷9=180÷9
x=20
底角度数是:
4x=4×20=80°
答:这个三角形的一个底角是80°。
19.一个等腰三角形,它的顶角是一个底角的2倍。这个等腰三角形的顶角是多少度?
【解答】解:180÷(2+1+1)×2
=180÷4×2
=90(度)
答:这个三角形的顶角是90°。
20.如果一个三角形的三条边长度都是整厘米数,第一条边长度是5cm,第二条边的长度比6厘米长而且比10厘米短,第三边的长度最短是多少厘米?最长是多少厘米?
【解答】解:若第二条边是9厘米,那么第三边最长是:
5+9=14(厘米)
14﹣1=13(厘米)
若第二条边是7厘米,那么第三边最短是:
7﹣5=2(厘米)
2+1=3(厘米)
答:第三边的长度最短是3厘米,最长是13厘米。
21.一个三角形中,∠A的度数是27.5°,∠B的度数是∠A的1.6倍,那么∠C是多少度?这是一个什么三角形?
【解答】解:∠B=27.5°×1.6=44°
∠C=180°﹣(27.5°+44°)=108.5°
108.5°>90°
答:∠C=108.5°,这是一个钝角三角形.
22.李爷爷家有一块三角形的菜地,菜地的最大内角是120°,是最小角的四倍,这块三角形菜地其它两个角各是多少度?按边分,这是一个什么三角形菜地?
【解答】解:120°÷4=30°
180°﹣120°﹣30°=30°
答:这块三角形菜地其它两个角都是30°,这是一个等腰三角形.
23.如果两个三角形3条边的长度分别相等,那么这两个三角形3个角的度数也分别相等吗?
【解答】解:如果两个三角形3条边的长度分别相等,那么这两个三角形3个角的度数也分别相等。
六.操作题(共2小题)
24.在点子图上按要求画图。
【解答】解:作图如下:
(画法不唯一)
25.求下面各角的度数.
(1)如图1,∠B=∠C=70度∠A= 40°
(2)如图2,∠B是直角,∠C=65度,∠A= 25° .
【解答】解:(1)180°﹣70°×2
=180°﹣140°
=40°
(2)180°﹣90°﹣65°
=90°﹣65°
=25°
故答案为:40°、25°.
一.选择题(共5小题)
1.一个三角形的两条边分别是6厘米和7厘米,那么第三条边的长度最长是( )
A.13厘米 B.12厘米 C.10厘米 D.15厘米
2.一个三角尺上有( )个锐角。
A.1 B.2 C.3
3.在三角形三个内角中,∠1=∠2+∠3,那么这个三角形一定是( )三角形.
A.钝角 B.直角 C.锐角 D.等腰
4.一个三角形至少有( )个锐角.
A.1 B.2 C.3 D.无法确定
5.把一个等边三角形平均分成两个直角三角形,其中一个直角三角形的两个锐角分别是( )
A.30°和30° B.30°和60° C.60°和60°
二.填空题(共5小题)
6.等腰三角形的底角是35°,顶角是 。等边三角形的每个内角都是 。
7.直角三角形三个角的度数分别是60°、 和 。
8.一个三角形的两条边长分别是3分米、8分米,第三条边可能是 分米。(多选少选不得分)
A.5
B.9
C.12
D.6
9.在一个三角形中,一个锐角是30°,截去这个角(如图所示),剩下图形的内角和是 °。
10.一个直角三角形的一个锐角是63度,另一内角是 .
三.判断题(共5小题)
11.锐角三角形的内角和小于钝角三角形的内角和. .
12.三角形不容易变形,具有稳定性。
13.三角形中任意两边之和一定大于第三边。
14.用3厘米、4厘米、5厘米长的三根绳子不能围成三角形.
15.锐角三角形任意两个锐角的和一定大于90°. .
四.计算题(共2小题)
16.求出下面各角的度数。
17.求出下面各角的度数。
五.应用题(共6小题)
18.一个等腰三角形,它的一个底角是顶角的4倍,这个三角形的一个底角是多少度?
19.一个等腰三角形,它的顶角是一个底角的2倍。这个等腰三角形的顶角是多少度?
20.如果一个三角形的三条边长度都是整厘米数,第一条边长度是5cm,第二条边的长度比6厘米长而且比10厘米短,第三边的长度最短是多少厘米?最长是多少厘米?
21.一个三角形中,∠A的度数是27.5°,∠B的度数是∠A的1.6倍,那么∠C是多少度?这是一个什么三角形?
22.李爷爷家有一块三角形的菜地,菜地的最大内角是120°,是最小角的四倍,这块三角形菜地其它两个角各是多少度?按边分,这是一个什么三角形菜地?
23.如果两个三角形3条边的长度分别相等,那么这两个三角形3个角的度数也分别相等吗?
六.操作题(共2小题)
24.在点子图上按要求画图。
25.求下面各角的度数.
(1)如图1,∠B=∠C=70度∠A=
(2)如图2,∠B是直角,∠C=65度,∠A= .
(进阶篇)2023-2024学年下学期小学数学人教新版四年级第5章练习卷
参考答案与试题解析
一.选择题(共5小题)
1.一个三角形的两条边分别是6厘米和7厘米,那么第三条边的长度最长是( )
A.13厘米 B.12厘米 C.10厘米 D.15厘米
【解答】解:7﹣6<第三边<7+6,
即1厘米<第三边<13厘米。
即第三边在1厘米~13厘米之间(不包括1厘米和13厘米)。
答:第三条边的长度最长是12厘米,最短是2厘米。
故选:B。
2.一个三角尺上有( )个锐角。
A.1 B.2 C.3
【解答】解:一个三角尺上有2个锐角。
故选:B。
3.在三角形三个内角中,∠1=∠2+∠3,那么这个三角形一定是( )三角形.
A.钝角 B.直角 C.锐角 D.等腰
【解答】解:由分析得:在三角形三个内角中,∠1=∠2+∠3,也就是180÷2=90(度),90÷2=45(度),那么这个三角形一定是直角三角形.
故选:B.
4.一个三角形至少有( )个锐角.
A.1 B.2 C.3 D.无法确定
【解答】解:假设三角形中锐角的个数少于2个,那么三角形中就会出现两个或两个以上的角是钝角或直角,
两个钝角或两个直角的和加上第三个角的度数一定大于180°,这就违背了三角形内角和是180°的性质,
所以一个三角形至少有2个锐角.
故选:B.
5.把一个等边三角形平均分成两个直角三角形,其中一个直角三角形的两个锐角分别是( )
A.30°和30° B.30°和60° C.60°和60°
【解答】解:60°÷2=30°
答:其中一个直角三角形的两个锐角分别是30°和60°。
故选:B。
二.填空题(共5小题)
6.等腰三角形的底角是35°,顶角是 110° 。等边三角形的每个内角都是 60° 。
【解答】解:180°﹣35°×2
=180°﹣70°
=110°
180°÷3=60°
答:等腰三角形的底角是35°,顶角是110°,等边三角形的每个内角都是60°。
故答案为:110°,60°。
7.直角三角形三个角的度数分别是60°、 90° 和 30° 。
【解答】解:180°﹣90°﹣60°=30°
答:如果是直角三角形,三个角分别是60o,90°,30°。
故答案为:90°,30°。
8.一个三角形的两条边长分别是3分米、8分米,第三条边可能是 B或D 分米。(多选少选不得分)
A.5
B.9
C.12
D.6
【解答】解:由三角形的特性可知:8分米﹣3分米<第三条边<3分米+8分米,
即5分米<第三条边<11分米,所以结合选项可知,第三条边可能是9分米或6分米。
故答案为:B或D。
9.在一个三角形中,一个锐角是30°,截去这个角(如图所示),剩下图形的内角和是 360 °。
【解答】解:剩下的图形可以分成两个三角形,所以剩下图形的内角和是180°×2=360°。
答:剩下图形的内角和是360°。
故答案为:360。
10.一个直角三角形的一个锐角是63度,另一内角是 27° .
【解答】解:直角三角形中有一个角是90°,
所以另一个锐角为90°﹣63°=27°,
答:另一个锐角是27°.
故答案为:27°.
三.判断题(共5小题)
11.锐角三角形的内角和小于钝角三角形的内角和. × .
【解答】解:因为任何三角形内角和都是180°,所以原题说法是错误的.
故答案为:×.
12.三角形不容易变形,具有稳定性。 √
【解答】解:例如:用一根钢条将一扇打开的玻璃窗支撑起来,这样风就不容易吹动窗户,这里所用的原理就是三角形的稳定性。如下图所示:
故答案为:√。
13.三角形中任意两边之和一定大于第三边。 √
【解答】解:三角形中任意两边之和一定大于第三边。原题说法正确。
故答案为:√。
14.用3厘米、4厘米、5厘米长的三根绳子不能围成三角形. ×
【解答】解:3+4>5
5﹣3<4
所以用3厘米、4厘米、5厘米的三根绳子能围成一个三角形,所以本题说法错误;
故答案为:×.
15.锐角三角形任意两个锐角的和一定大于90°. √ .
【解答】解:如果两个锐角和不大于90°,那么第三个角将大于等于90°,就不再是锐角三角形.
所以上面的说法是正确的.
故答案为:√.
四.计算题(共2小题)
16.求出下面各角的度数。
【解答】解:根据图示可知三角形为直角三角形,
∠2=180°﹣90°﹣58°=32°
17.求出下面各角的度数。
【解答】解:∠1=180°﹣62°﹣46°=72°
五.应用题(共6小题)
18.一个等腰三角形,它的一个底角是顶角的4倍,这个三角形的一个底角是多少度?
【解答】解:设顶角是x度,则底角就是4x度。
x+4x+4x=180°
9x=180°
9x÷9=180÷9
x=20
底角度数是:
4x=4×20=80°
答:这个三角形的一个底角是80°。
19.一个等腰三角形,它的顶角是一个底角的2倍。这个等腰三角形的顶角是多少度?
【解答】解:180÷(2+1+1)×2
=180÷4×2
=90(度)
答:这个三角形的顶角是90°。
20.如果一个三角形的三条边长度都是整厘米数,第一条边长度是5cm,第二条边的长度比6厘米长而且比10厘米短,第三边的长度最短是多少厘米?最长是多少厘米?
【解答】解:若第二条边是9厘米,那么第三边最长是:
5+9=14(厘米)
14﹣1=13(厘米)
若第二条边是7厘米,那么第三边最短是:
7﹣5=2(厘米)
2+1=3(厘米)
答:第三边的长度最短是3厘米,最长是13厘米。
21.一个三角形中,∠A的度数是27.5°,∠B的度数是∠A的1.6倍,那么∠C是多少度?这是一个什么三角形?
【解答】解:∠B=27.5°×1.6=44°
∠C=180°﹣(27.5°+44°)=108.5°
108.5°>90°
答:∠C=108.5°,这是一个钝角三角形.
22.李爷爷家有一块三角形的菜地,菜地的最大内角是120°,是最小角的四倍,这块三角形菜地其它两个角各是多少度?按边分,这是一个什么三角形菜地?
【解答】解:120°÷4=30°
180°﹣120°﹣30°=30°
答:这块三角形菜地其它两个角都是30°,这是一个等腰三角形.
23.如果两个三角形3条边的长度分别相等,那么这两个三角形3个角的度数也分别相等吗?
【解答】解:如果两个三角形3条边的长度分别相等,那么这两个三角形3个角的度数也分别相等。
六.操作题(共2小题)
24.在点子图上按要求画图。
【解答】解:作图如下:
(画法不唯一)
25.求下面各角的度数.
(1)如图1,∠B=∠C=70度∠A= 40°
(2)如图2,∠B是直角,∠C=65度,∠A= 25° .
【解答】解:(1)180°﹣70°×2
=180°﹣140°
=40°
(2)180°﹣90°﹣65°
=90°﹣65°
=25°
故答案为:40°、25°.
