【提分必刷】江苏地区六年级数学期末考试提分卷6(苏教版含解析)
文档属性
| 名称 | 【提分必刷】江苏地区六年级数学期末考试提分卷6(苏教版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-10 20:08:17 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【提分必刷】江苏地区六年级数学期末考试提分卷6(苏教版含解析)
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.把一个正方体的棱长缩小4倍,表面积( )。
A.缩小4倍 B.缩小16倍 C.扩大8倍
2.一个长方形,长与宽的比是3∶2.已知长是6米,那么面积是( )平方米。
A.24 B.54 C. D.
3.如图,数a的倒数是( )。
A.小于1 B.大于1 C.等于1 D.无法确定
4.比的前项扩大2倍,后项缩小到它的,比值就( )
A.缩小到它的 B.扩大2倍
C.扩大8倍
5.小民和小林进行投篮练习。小民的命中率是65%,小林的命中率是70%。谁投中的次数多些?( )
A.小民多些 B.小林多些 C.两人一样多 D.可能小民多,也可能小林多
6.下面与∶的比值相等的比是( ).
A.2∶3 B.3∶2 C.4∶3
7.男生人数是女生人数的 ,正确的等量关系式是( )
A.男生人数× =女生人数
B.女生人数× =男生人数
C.女生人数÷ =男生人数
8.分别用8个同样大的小正方体拼成一个正方体和一个长方体,它们的表面积相比( )
A.正方体大 B.长方体大 C.同样大
9.六(1)班中男生占,则女生占男生的( )。
A. B. C. D.
10.如图中,大、小两个正方形的阴影部分的面积比是,那么大、小正方形的面积比是( )。
A. B. C. D.
二、填空题
11.一堆煤有15吨,运走它的,还余下( )吨,再运走 吨,还余下( )吨.
12.12和8的最大公因数是 ,最小公倍数是 0.8:0.2的比值是 ,最简整数比是 .
13.把∶50%化成最简单的整数比是( ),其比值是( )。
14.把化成最简整数比是( )∶( ),比值是( )。
15.在如表格的长方形里涂上颜色,表示×的意义.
16.李师傅加工一批零件,第一个星期加工了420个,第二个星期比第一个星期多加工了,两个星期一共加工了( )个零件.
17.下图的平行四边形中,乙的面积占平行四边形面积的,乙的面积与丙的面积的比是( )。
18.前进小学六年级有200个学生,其中有120个女生,男生人数与女生人数的最简单的整数比是 .
19.用30米长的篱笆围成一个长方形鸡舍,若长方形一面靠墙,则长= 米,宽= 米时面积最大,最大面积是 .
20.在括号里填上合适的单位名称。
(1)一个乒乓球的体积大约是33( )。
(2)一盒纯牛奶的净含量是250( )。
三、判断题
21.4千克∶80千克的比值是千克。( )
22.栽100棵树苗,死了5棵,又补栽了5棵全部成活,这次植树的成活率是100%。( )
23.8小时15分等于8小时. ( )
24.大小两个正方体的棱长比是3∶2,那么它们的体积比是9∶4。( )
25.( )
26.把8∶15的后项增加60,要使比值不变,前项应乘4。( )
27.正方体的棱长扩大2倍,它的体积就扩大8倍。( )
28.已知A÷=B÷,A、B都不为零,那么A一定大于B.( )
四、计算题
29.求解方程。
40%X=3.2 X+20%X=48 X-X=48
30.解方程。
五、解答题
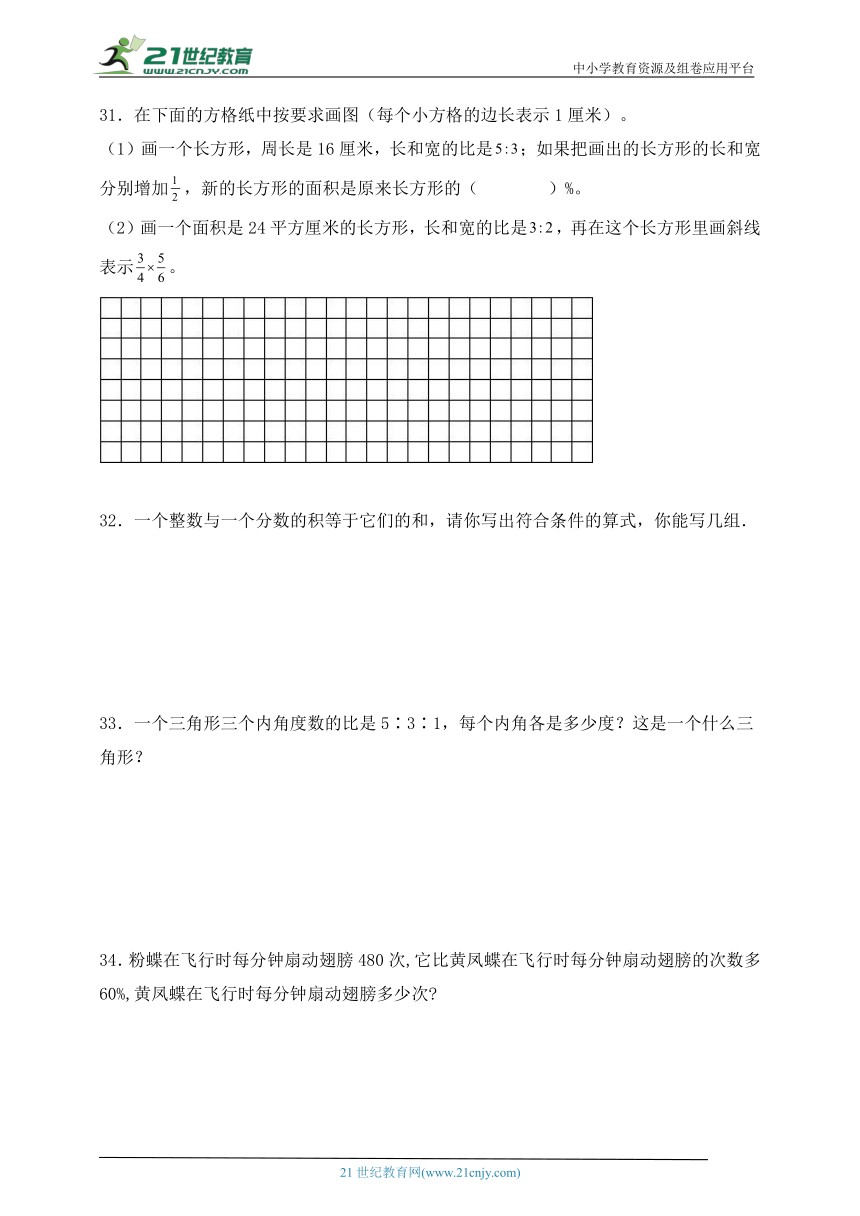
31.在下面的方格纸中按要求画图(每个小方格的边长表示1厘米)。
(1)画一个长方形,周长是16厘米,长和宽的比是;如果把画出的长方形的长和宽分别增加,新的长方形的面积是原来长方形的( )%。
(2)画一个面积是24平方厘米的长方形,长和宽的比是,再在这个长方形里画斜线表示。
32.一个整数与一个分数的积等于它们的和,请你写出符合条件的算式,你能写几组.
33.一个三角形三个内角度数的比是5∶3∶1,每个内角各是多少度?这是一个什么三角形?
34.粉蝶在飞行时每分钟扇动翅膀480次,它比黄凤蝶在飞行时每分钟扇动翅膀的次数多60%,黄凤蝶在飞行时每分钟扇动翅膀多少次
35.根据题意列出综合算式。(不计算)
李阿姨将12000元钱存入银行,存期为3年,年利率为2.75%,到期去取时,李阿姨可得到多少利息?
列式:
参考答案:
1.B
【分析】根据正方体的表面积公式:S=6a2,再根据因数与积的变化规律,积扩大或缩小的倍数等于因数扩大或缩小倍数的乘积。据此解答。
【详解】把一个正方体的棱长缩小4倍,表面积缩小4×4=16倍
故选:B。
【点睛】明确正方体表面积的计算公式是解决本题的关键。
2.A
【详解】略
3.B
【分析】数a是大于0,小于1的数,那么a就是真分数,真分数的倒数是假分数,假分数是大于1的数。
【详解】数a的倒数是大于1的数。
故答案为:B
【点睛】此题主要考查学生对倒数的理解,根据真分数和假分数的概念进行解答即可。
4.C
【详解】比的前项扩大2倍,后项缩小到它的,比值就扩大2=8倍;
故选C.
5.D
【详解】略
6.B
【解析】略
7.B
【详解】解:男生人数是女生人数的 ,正确的等量关系式是:男生人数=女生人数× ;
故选B.
根据一个数乘分数的意义:求这个数的几分之几是多少,即可得出本题的等量关系式.
8.B
【解析】略
9.C
【分析】把六(1)班人数看作单位“1”,男生占,则女生占全班的(1-),求女生占男生的几分之几,用(1-)÷即可求解。
【详解】
=×
即女生占男生的。
故答案为:C
【点睛】本题考查求一个数是另一个数的几分之几,用除法解决,要重点掌握。
10.A
【分析】观察图形可知,大正方形的面积是其阴影部分的4倍;小正方形的面积是其阴影部分的4倍;大、小两个正方形的阴影部分的面积比是2∶1,则大正方形面积∶小正方形面积=(2×4)∶(1×4),化简即可解答。
【详解】(2×4)∶(1×4)
=8∶4
=(8÷4)∶(4÷4)
=2∶1
如图中,大、小两个正方形的阴影部分的面积比是,那么大、小正方形的面积比是2∶1。
故答案为:A
【点睛】解答本题的关键是理解阴影部分与正方形面积的关系。
11. 10 9.4
【详解】略
12.4,24;4,4:1
【详解】试题分析:(1)利用求两个数的最大公约数和最小公倍数的方法:两个数的公有质因数连乘积就是它们的最大公约数,两个数的公有质因数和它们独有的质因数的连乘积就是它们的最小公倍数,由此解决问题即可;
(2)求比值的方法:用比的前项除以比的后项即得比值,比值是一个数,可以是小数,可以是分数,也可以是整数.化简比是根据比的性质将比化成最简比的过程,结果仍是一个比.由此计算即可.
解:(1)12=2×2×3,
8=2×2×2,
所以12和8的最大公约数:2×2=4,
最小公倍数是2×2×2×3=24.
(2)0.8:0.2=0.8÷0.2=4,
故0.8:0.2的比值是4,
0.8:0.2=(0.8×5):(0.2×5)=4:1,
故0.8:0.2的最简整数比是4:1.
故答案为4,24;4,4:1.
点评:此题考查了求几个数的最大公约数和最小公倍数的方法;同时考查求比值和化简比的方法,要注意区分:求比值的结果是一个数;化简比的结果仍是一个比.
13. 5∶4 1.25
【分析】(1)根据比的基本性质,即比的前项和后项同时乘或除以一个相同的数(0除外),比值不变,进而把比化成最简比;
(2)用最简比的前项除以后项即得比值。
【详解】∶50%=∶=(×8)∶(×8)=5∶4
∶50%=∶=÷=×2=1.25
【点睛】此题考查化简比和求比值的方法,要注意区分:化简比的结果是一个比;而求比值的结果是一个数。
14. 4 1 4
【分析】根据比的基本性质,比的前项和后项同时乘或除以一个相同的数(0除外),比值不变,据此化简比即可;用比的前项除以比的后项即可求出比值。
【详解】
=(14×10)∶(3.5×10)
=140∶35
=(140÷35)∶(35÷35)
=4∶1
4÷1=4
则把化成最简整数比是4∶1,比值是4。
15.
【详解】试题分析:把一个长方形平均分成2份,先涂其中的1份;再把这1份平均分成3份,涂其中的2份即可.
点评:此题用涂色的方法考查了分数的意义.
16.1008
【详解】把第一个星期加工的零件看作单位“1”,则有第二个星期加工的零件数是420×(1+)=580(个),两个星期一共加工了588+420=1008(个).
17.2∶5
【分析】由图可知,三角形丙与平行四边形是等底等高的,所以三角形丙的面积是平行四边形的 ,因为乙的面积占平行四边形面积的,所以乙的面积与丙的面积的比是∶,化简即可。
【详解】由分析可知,乙的面积与丙的面积的比是∶,化简得2∶5。
【点睛】此题考查了多边形面积与比的综合应用,找出丙的面积占平行四边形的分率是解题关键。
18.2:3
【详解】900千米=90000000厘米,15:90000000=1:6000000,
答:这幅地图的比例尺是1:6000000.
故答案为1:6000000.
【分析】本题考点:图上距离与实际距离的换算(比例尺的应用).
此类题做题的关键是:利用比例尺的意义,代入数据计算,得出结论.
求比例尺,根据比例尺的概念:图上距离和实际距离的比,代入数据,进行解答,即可解决问题.
19.15,,平方米
【详解】试题分析:设养鸡场宽为x米,则长为(30﹣2x)米,再通过列表法由面积公式求解.
解:设养鸡场宽为x米,则长为(30﹣2x)米,根据题意得列表如下:
长 28 20 15 14 10
宽 1 5 8 10
面积 28 100 112 100
当x=时,30﹣2x=15,最大面积为.
故答案为15,,平方米.
点评:本题主要考查长方形面积的应用,借助列表法解决实际问题.
20. 立方厘米 毫升
【分析】根据生活经验、对容积单位、体积单位和数据的大小,可知计量一个乒乓球的体积应用“立方厘米”做单位;计量一盒纯牛奶的净含量应用“毫升”做单位。
【详解】(1)一个乒乓球的体积大约是33立方厘米。
(2)一盒纯牛奶的净含量是250毫升。
【点睛】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活的选择。
21.×
【分析】根据题意,用比的前项除以后项求出比值,然后判断即可。
【详解】4千克∶80千克
=4÷80
=
由于比值不能带单位,所以原题说法错误。
故答案为:×
【点睛】此题主要考查了求比值的方法,另外还要注意求同类量的比的比值,结果是不带单位的。
22.×
【分析】栽100棵树苗,死了5棵,成活了95棵,又补栽了5棵全部成活,那么总共栽了105棵,成活100棵,100棵除以105棵得到成活率。
【详解】(棵)
成活率并不是100%,题干阐述错误。
故答案为:×。
【点睛】成活率、出勤率等常见百分率的计算,都要用符合要求的数量除以总数量。
23.×
【详解】略
24.×
【分析】大小两个正方体的棱长比是3∶2,可设大正方体的棱长是3a,小正方体的棱长是2a,根据正方体的体积=棱长×棱长×棱长,表示出它们的体积,进而写出它们的体积比判断即可。
【详解】可设大正方体的棱长是3a,小正方体的棱长是2a,则大正方体与小正方体的体积比是(3a)3∶(2a)3,化简得27∶8。
故答案为:×
【点睛】两个正方体的体积之比等于它们的棱长的立方之比。
25.×
【解析】略
26.×
【分析】根据比的性质,比的前项和后项同时乘或除以相同的数(0除外)比值不变,据此解答。
【详解】比的后项增加60后是15+60=75,扩大了75÷15=5倍,前项也应该扩大5倍。所以前项应该乘5。原题说法错误。
故答案为:×
【点睛】掌握比的性质,并能灵活运用。
27.√
【分析】正方体的体积=棱长×棱长×棱长,再根据因数与积的变化规律,积扩大的倍数等于因数扩大倍数的乘积,据此判断。
【详解】正方体的棱长扩大2倍,正方体的体积扩大2×2×2=8倍。
故答案为:√
【点睛】此题主要考查正方体的体积公式的灵活运用,以及因数与积的变化规律的应用。
28.×
【解析】略
29.X=8;X=40;X=128
【分析】方程两边同时除以40%即可;
将方程化为(1+20%)X=48,再将方程两边同时除以(1+20%)即可;
将方程化为(1-)X=48,再将方程两边同时除以(1-)即可;
【详解】40%X=3.2
解:X=3.2÷40%
X=8
X+20%X=48
解:(1+20%)X=48
X=48÷(1+20%)
X=40
X-X=48
解:(1-)X=48
X=48÷(1-)
X=128
【点睛】本题主要考查方程的解法,认真计算即可。
30.x=;x=20
【分析】,先计算1-的差,再除以,即可解答;
40%x+25%x=13,先计算40%与25%的和,再用13除以40%与25%的和,即可解答。
【详解】
解:x=1-
x=
x=÷
x=×2
x=
解:65%x=13
x=13÷65%
x=20
31.(1)作图见详解;225;
(2)作图见详解
【分析】(1)长方形周长是16厘米,长和宽的比是;根据按比例分配的方法分别求出长和宽,据此画出长方形,把画出的长方形的长和宽分别增加,即增加后的长是原来的(1+),增加后的宽是原来的(1+),那么新的长方形的面积是原来长方形的(1+)×(1+);
(2)面积是24平方厘米的长方形,长和宽的比是,因为6×4=24,且6∶4=3∶2,所以长方形的长是6厘米,宽是4厘米,据此画出长方形,再把这个长方形平均分成4份,用单斜线表示其中的3份,再把这3份平均分成6份,用双斜线表示其中的5份。
【详解】(1)16÷2÷(5+3)
=8÷8
=1(厘米)
1×5=5(厘米)
1×3=3(厘米)
(1+)×(1+)
=×
=
=225%
(1)(2)作图如下:
【点睛】此题考查了画指定周长、面积的长方形,解题的关键是根据比求出长方形的长和宽。
32.如3×=3+,
4×=4+,
5×=5+,
这个整数,同这个分数的关系是这个整数是分数的分子,分母是比它小1的数,分母是不等于1的整数.
所以可以写无数组.
【详解】试题分析:因一个整数同一个分数相加,它们的和一定大于这个整数,一个非零的整数只能同大于1的分数相乘,它们的积,才大于这个整数.据此解答.
解:因一个整数同一个分数相加,它们的和一定大于这个整数,一个非零的整数只能同大于1的分数相乘,它们的积,才大于这个整数,所以分数一定是大于1的假分数.
点评:本题的关键是找出符合这样条件的数的规律.
33.20°;60°;100°;钝角三角形
【分析】三角形内角和是180°,三个内角度数比是5∶3∶1,就是把180°分成(5+3+1)份,根据份数分别求出三个内角的度数,再根据最大角的度数确定三角形的类别。
【详解】180°÷(5+3+1)
=180°÷(8+1)
=180°÷9
=20°
三个内角分别是:20°×1=20°
20°×3=60°
20×5=100°
100°>90°
是钝角三角形
答:内角是20°、60°、100°,这是一个钝角三角形。
【点睛】本题考查比的应用和三角形的分类,明确三角形内角和,掌握分配的方法是解答本题的关键。
34.300次
【详解】480÷(1+60%)=300(次)
35.
【分析】根据利息=本金×利率×存期,列式即可。
【详解】根据分析,列式为:
【点睛】关键是掌握利息求法,取款时银行多支付的钱叫利息。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【提分必刷】江苏地区六年级数学期末考试提分卷6(苏教版含解析)
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.把一个正方体的棱长缩小4倍,表面积( )。
A.缩小4倍 B.缩小16倍 C.扩大8倍
2.一个长方形,长与宽的比是3∶2.已知长是6米,那么面积是( )平方米。
A.24 B.54 C. D.
3.如图,数a的倒数是( )。
A.小于1 B.大于1 C.等于1 D.无法确定
4.比的前项扩大2倍,后项缩小到它的,比值就( )
A.缩小到它的 B.扩大2倍
C.扩大8倍
5.小民和小林进行投篮练习。小民的命中率是65%,小林的命中率是70%。谁投中的次数多些?( )
A.小民多些 B.小林多些 C.两人一样多 D.可能小民多,也可能小林多
6.下面与∶的比值相等的比是( ).
A.2∶3 B.3∶2 C.4∶3
7.男生人数是女生人数的 ,正确的等量关系式是( )
A.男生人数× =女生人数
B.女生人数× =男生人数
C.女生人数÷ =男生人数
8.分别用8个同样大的小正方体拼成一个正方体和一个长方体,它们的表面积相比( )
A.正方体大 B.长方体大 C.同样大
9.六(1)班中男生占,则女生占男生的( )。
A. B. C. D.
10.如图中,大、小两个正方形的阴影部分的面积比是,那么大、小正方形的面积比是( )。
A. B. C. D.
二、填空题
11.一堆煤有15吨,运走它的,还余下( )吨,再运走 吨,还余下( )吨.
12.12和8的最大公因数是 ,最小公倍数是 0.8:0.2的比值是 ,最简整数比是 .
13.把∶50%化成最简单的整数比是( ),其比值是( )。
14.把化成最简整数比是( )∶( ),比值是( )。
15.在如表格的长方形里涂上颜色,表示×的意义.
16.李师傅加工一批零件,第一个星期加工了420个,第二个星期比第一个星期多加工了,两个星期一共加工了( )个零件.
17.下图的平行四边形中,乙的面积占平行四边形面积的,乙的面积与丙的面积的比是( )。
18.前进小学六年级有200个学生,其中有120个女生,男生人数与女生人数的最简单的整数比是 .
19.用30米长的篱笆围成一个长方形鸡舍,若长方形一面靠墙,则长= 米,宽= 米时面积最大,最大面积是 .
20.在括号里填上合适的单位名称。
(1)一个乒乓球的体积大约是33( )。
(2)一盒纯牛奶的净含量是250( )。
三、判断题
21.4千克∶80千克的比值是千克。( )
22.栽100棵树苗,死了5棵,又补栽了5棵全部成活,这次植树的成活率是100%。( )
23.8小时15分等于8小时. ( )
24.大小两个正方体的棱长比是3∶2,那么它们的体积比是9∶4。( )
25.( )
26.把8∶15的后项增加60,要使比值不变,前项应乘4。( )
27.正方体的棱长扩大2倍,它的体积就扩大8倍。( )
28.已知A÷=B÷,A、B都不为零,那么A一定大于B.( )
四、计算题
29.求解方程。
40%X=3.2 X+20%X=48 X-X=48
30.解方程。
五、解答题
31.在下面的方格纸中按要求画图(每个小方格的边长表示1厘米)。
(1)画一个长方形,周长是16厘米,长和宽的比是;如果把画出的长方形的长和宽分别增加,新的长方形的面积是原来长方形的( )%。
(2)画一个面积是24平方厘米的长方形,长和宽的比是,再在这个长方形里画斜线表示。
32.一个整数与一个分数的积等于它们的和,请你写出符合条件的算式,你能写几组.
33.一个三角形三个内角度数的比是5∶3∶1,每个内角各是多少度?这是一个什么三角形?
34.粉蝶在飞行时每分钟扇动翅膀480次,它比黄凤蝶在飞行时每分钟扇动翅膀的次数多60%,黄凤蝶在飞行时每分钟扇动翅膀多少次
35.根据题意列出综合算式。(不计算)
李阿姨将12000元钱存入银行,存期为3年,年利率为2.75%,到期去取时,李阿姨可得到多少利息?
列式:
参考答案:
1.B
【分析】根据正方体的表面积公式:S=6a2,再根据因数与积的变化规律,积扩大或缩小的倍数等于因数扩大或缩小倍数的乘积。据此解答。
【详解】把一个正方体的棱长缩小4倍,表面积缩小4×4=16倍
故选:B。
【点睛】明确正方体表面积的计算公式是解决本题的关键。
2.A
【详解】略
3.B
【分析】数a是大于0,小于1的数,那么a就是真分数,真分数的倒数是假分数,假分数是大于1的数。
【详解】数a的倒数是大于1的数。
故答案为:B
【点睛】此题主要考查学生对倒数的理解,根据真分数和假分数的概念进行解答即可。
4.C
【详解】比的前项扩大2倍,后项缩小到它的,比值就扩大2=8倍;
故选C.
5.D
【详解】略
6.B
【解析】略
7.B
【详解】解:男生人数是女生人数的 ,正确的等量关系式是:男生人数=女生人数× ;
故选B.
根据一个数乘分数的意义:求这个数的几分之几是多少,即可得出本题的等量关系式.
8.B
【解析】略
9.C
【分析】把六(1)班人数看作单位“1”,男生占,则女生占全班的(1-),求女生占男生的几分之几,用(1-)÷即可求解。
【详解】
=×
即女生占男生的。
故答案为:C
【点睛】本题考查求一个数是另一个数的几分之几,用除法解决,要重点掌握。
10.A
【分析】观察图形可知,大正方形的面积是其阴影部分的4倍;小正方形的面积是其阴影部分的4倍;大、小两个正方形的阴影部分的面积比是2∶1,则大正方形面积∶小正方形面积=(2×4)∶(1×4),化简即可解答。
【详解】(2×4)∶(1×4)
=8∶4
=(8÷4)∶(4÷4)
=2∶1
如图中,大、小两个正方形的阴影部分的面积比是,那么大、小正方形的面积比是2∶1。
故答案为:A
【点睛】解答本题的关键是理解阴影部分与正方形面积的关系。
11. 10 9.4
【详解】略
12.4,24;4,4:1
【详解】试题分析:(1)利用求两个数的最大公约数和最小公倍数的方法:两个数的公有质因数连乘积就是它们的最大公约数,两个数的公有质因数和它们独有的质因数的连乘积就是它们的最小公倍数,由此解决问题即可;
(2)求比值的方法:用比的前项除以比的后项即得比值,比值是一个数,可以是小数,可以是分数,也可以是整数.化简比是根据比的性质将比化成最简比的过程,结果仍是一个比.由此计算即可.
解:(1)12=2×2×3,
8=2×2×2,
所以12和8的最大公约数:2×2=4,
最小公倍数是2×2×2×3=24.
(2)0.8:0.2=0.8÷0.2=4,
故0.8:0.2的比值是4,
0.8:0.2=(0.8×5):(0.2×5)=4:1,
故0.8:0.2的最简整数比是4:1.
故答案为4,24;4,4:1.
点评:此题考查了求几个数的最大公约数和最小公倍数的方法;同时考查求比值和化简比的方法,要注意区分:求比值的结果是一个数;化简比的结果仍是一个比.
13. 5∶4 1.25
【分析】(1)根据比的基本性质,即比的前项和后项同时乘或除以一个相同的数(0除外),比值不变,进而把比化成最简比;
(2)用最简比的前项除以后项即得比值。
【详解】∶50%=∶=(×8)∶(×8)=5∶4
∶50%=∶=÷=×2=1.25
【点睛】此题考查化简比和求比值的方法,要注意区分:化简比的结果是一个比;而求比值的结果是一个数。
14. 4 1 4
【分析】根据比的基本性质,比的前项和后项同时乘或除以一个相同的数(0除外),比值不变,据此化简比即可;用比的前项除以比的后项即可求出比值。
【详解】
=(14×10)∶(3.5×10)
=140∶35
=(140÷35)∶(35÷35)
=4∶1
4÷1=4
则把化成最简整数比是4∶1,比值是4。
15.
【详解】试题分析:把一个长方形平均分成2份,先涂其中的1份;再把这1份平均分成3份,涂其中的2份即可.
点评:此题用涂色的方法考查了分数的意义.
16.1008
【详解】把第一个星期加工的零件看作单位“1”,则有第二个星期加工的零件数是420×(1+)=580(个),两个星期一共加工了588+420=1008(个).
17.2∶5
【分析】由图可知,三角形丙与平行四边形是等底等高的,所以三角形丙的面积是平行四边形的 ,因为乙的面积占平行四边形面积的,所以乙的面积与丙的面积的比是∶,化简即可。
【详解】由分析可知,乙的面积与丙的面积的比是∶,化简得2∶5。
【点睛】此题考查了多边形面积与比的综合应用,找出丙的面积占平行四边形的分率是解题关键。
18.2:3
【详解】900千米=90000000厘米,15:90000000=1:6000000,
答:这幅地图的比例尺是1:6000000.
故答案为1:6000000.
【分析】本题考点:图上距离与实际距离的换算(比例尺的应用).
此类题做题的关键是:利用比例尺的意义,代入数据计算,得出结论.
求比例尺,根据比例尺的概念:图上距离和实际距离的比,代入数据,进行解答,即可解决问题.
19.15,,平方米
【详解】试题分析:设养鸡场宽为x米,则长为(30﹣2x)米,再通过列表法由面积公式求解.
解:设养鸡场宽为x米,则长为(30﹣2x)米,根据题意得列表如下:
长 28 20 15 14 10
宽 1 5 8 10
面积 28 100 112 100
当x=时,30﹣2x=15,最大面积为.
故答案为15,,平方米.
点评:本题主要考查长方形面积的应用,借助列表法解决实际问题.
20. 立方厘米 毫升
【分析】根据生活经验、对容积单位、体积单位和数据的大小,可知计量一个乒乓球的体积应用“立方厘米”做单位;计量一盒纯牛奶的净含量应用“毫升”做单位。
【详解】(1)一个乒乓球的体积大约是33立方厘米。
(2)一盒纯牛奶的净含量是250毫升。
【点睛】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活的选择。
21.×
【分析】根据题意,用比的前项除以后项求出比值,然后判断即可。
【详解】4千克∶80千克
=4÷80
=
由于比值不能带单位,所以原题说法错误。
故答案为:×
【点睛】此题主要考查了求比值的方法,另外还要注意求同类量的比的比值,结果是不带单位的。
22.×
【分析】栽100棵树苗,死了5棵,成活了95棵,又补栽了5棵全部成活,那么总共栽了105棵,成活100棵,100棵除以105棵得到成活率。
【详解】(棵)
成活率并不是100%,题干阐述错误。
故答案为:×。
【点睛】成活率、出勤率等常见百分率的计算,都要用符合要求的数量除以总数量。
23.×
【详解】略
24.×
【分析】大小两个正方体的棱长比是3∶2,可设大正方体的棱长是3a,小正方体的棱长是2a,根据正方体的体积=棱长×棱长×棱长,表示出它们的体积,进而写出它们的体积比判断即可。
【详解】可设大正方体的棱长是3a,小正方体的棱长是2a,则大正方体与小正方体的体积比是(3a)3∶(2a)3,化简得27∶8。
故答案为:×
【点睛】两个正方体的体积之比等于它们的棱长的立方之比。
25.×
【解析】略
26.×
【分析】根据比的性质,比的前项和后项同时乘或除以相同的数(0除外)比值不变,据此解答。
【详解】比的后项增加60后是15+60=75,扩大了75÷15=5倍,前项也应该扩大5倍。所以前项应该乘5。原题说法错误。
故答案为:×
【点睛】掌握比的性质,并能灵活运用。
27.√
【分析】正方体的体积=棱长×棱长×棱长,再根据因数与积的变化规律,积扩大的倍数等于因数扩大倍数的乘积,据此判断。
【详解】正方体的棱长扩大2倍,正方体的体积扩大2×2×2=8倍。
故答案为:√
【点睛】此题主要考查正方体的体积公式的灵活运用,以及因数与积的变化规律的应用。
28.×
【解析】略
29.X=8;X=40;X=128
【分析】方程两边同时除以40%即可;
将方程化为(1+20%)X=48,再将方程两边同时除以(1+20%)即可;
将方程化为(1-)X=48,再将方程两边同时除以(1-)即可;
【详解】40%X=3.2
解:X=3.2÷40%
X=8
X+20%X=48
解:(1+20%)X=48
X=48÷(1+20%)
X=40
X-X=48
解:(1-)X=48
X=48÷(1-)
X=128
【点睛】本题主要考查方程的解法,认真计算即可。
30.x=;x=20
【分析】,先计算1-的差,再除以,即可解答;
40%x+25%x=13,先计算40%与25%的和,再用13除以40%与25%的和,即可解答。
【详解】
解:x=1-
x=
x=÷
x=×2
x=
解:65%x=13
x=13÷65%
x=20
31.(1)作图见详解;225;
(2)作图见详解
【分析】(1)长方形周长是16厘米,长和宽的比是;根据按比例分配的方法分别求出长和宽,据此画出长方形,把画出的长方形的长和宽分别增加,即增加后的长是原来的(1+),增加后的宽是原来的(1+),那么新的长方形的面积是原来长方形的(1+)×(1+);
(2)面积是24平方厘米的长方形,长和宽的比是,因为6×4=24,且6∶4=3∶2,所以长方形的长是6厘米,宽是4厘米,据此画出长方形,再把这个长方形平均分成4份,用单斜线表示其中的3份,再把这3份平均分成6份,用双斜线表示其中的5份。
【详解】(1)16÷2÷(5+3)
=8÷8
=1(厘米)
1×5=5(厘米)
1×3=3(厘米)
(1+)×(1+)
=×
=
=225%
(1)(2)作图如下:
【点睛】此题考查了画指定周长、面积的长方形,解题的关键是根据比求出长方形的长和宽。
32.如3×=3+,
4×=4+,
5×=5+,
这个整数,同这个分数的关系是这个整数是分数的分子,分母是比它小1的数,分母是不等于1的整数.
所以可以写无数组.
【详解】试题分析:因一个整数同一个分数相加,它们的和一定大于这个整数,一个非零的整数只能同大于1的分数相乘,它们的积,才大于这个整数.据此解答.
解:因一个整数同一个分数相加,它们的和一定大于这个整数,一个非零的整数只能同大于1的分数相乘,它们的积,才大于这个整数,所以分数一定是大于1的假分数.
点评:本题的关键是找出符合这样条件的数的规律.
33.20°;60°;100°;钝角三角形
【分析】三角形内角和是180°,三个内角度数比是5∶3∶1,就是把180°分成(5+3+1)份,根据份数分别求出三个内角的度数,再根据最大角的度数确定三角形的类别。
【详解】180°÷(5+3+1)
=180°÷(8+1)
=180°÷9
=20°
三个内角分别是:20°×1=20°
20°×3=60°
20×5=100°
100°>90°
是钝角三角形
答:内角是20°、60°、100°,这是一个钝角三角形。
【点睛】本题考查比的应用和三角形的分类,明确三角形内角和,掌握分配的方法是解答本题的关键。
34.300次
【详解】480÷(1+60%)=300(次)
35.
【分析】根据利息=本金×利率×存期,列式即可。
【详解】根据分析,列式为:
【点睛】关键是掌握利息求法,取款时银行多支付的钱叫利息。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
