九下数学第26章二次函数 复习课件
图片预览

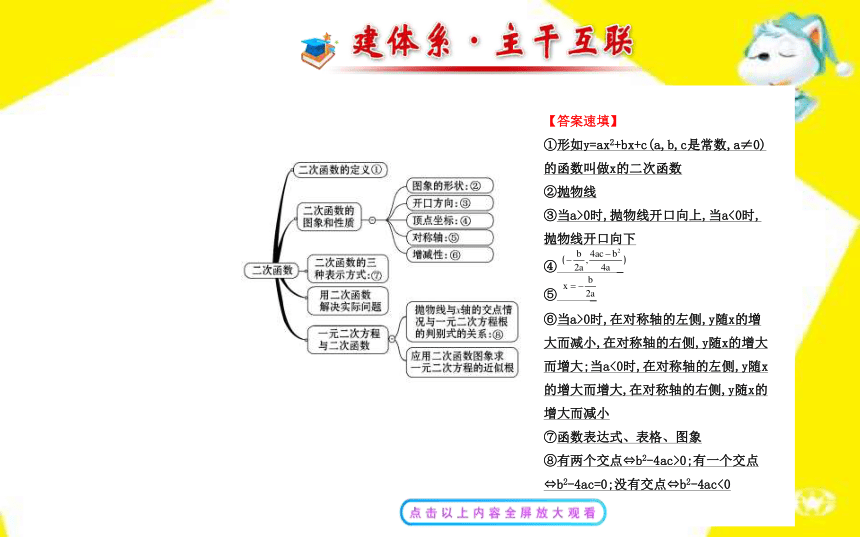









文档简介
课件48张PPT。阶段复习课
第 26 章主题1 二次函数的图象和性质
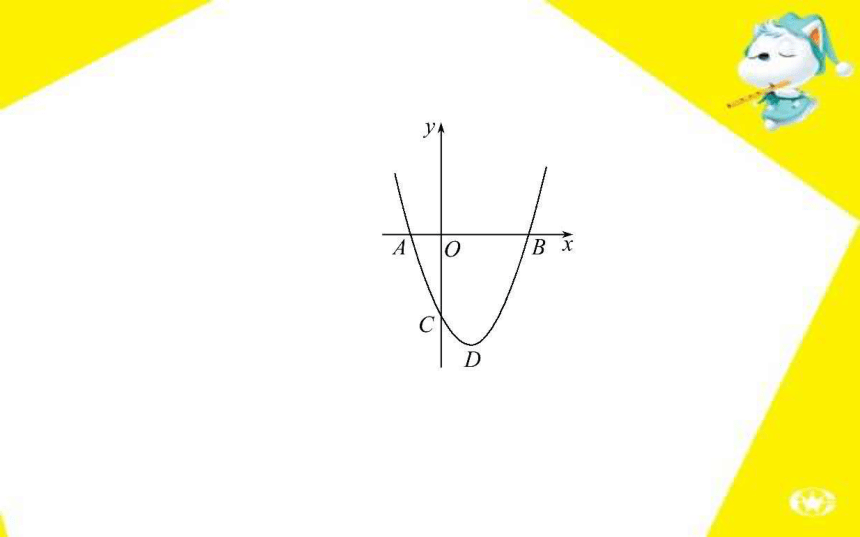
【主题训练1】(2014·安顺中考)如图,二次函数y=ax2+bx+c
(a>0)的图象的顶点为D,其图象与x轴的交点A,B的横坐标分别
为-1,3.与y轴负半轴交于点C.在下面五个结论中:
①2a-b=0;②a+b+c>0;③c=-3a;④只有当a= 时,△ABD是等腰
直角三角形;⑤使△ACB为等腰三角形的a的值可以有四个.其中
正确的结论是 .(只填序号)【解析】①∵函数图象与x轴的交点A,B的横坐标分别为-1,3,
∴对称轴为直线x=1,即:- =1,变形得:2a+b=0.
∴此结论错误;
②当x=1时,y=a+b+c<0,∴此结论错误;
③把(-1,0)和(3,0)代入表达式可得:
①×3+②得:12a+4c=0,即:c=-3a;
∴此结论正确;④当a= 时,由- =1可得b=-1;由a-b+c=0可得c=- ;
则D点的纵坐标为:
则D点到x轴的距离为2.连接AD,BD,∵顶点为点D,
∴AD=BD.又 AB=2,
可证△ABD是等腰直角三角形,
∴此结论正确;
⑤由上一步的结论可证此结论错误.
答案:③④【主题升华】系数a,b,c与二次函数的图象的关系
(1)a决定开口方向及开口大小.
当a>0时,开口向上,当a<0时,开口向下;|a|越大,抛物线的开口
越小.
(2)b和a共同决定抛物线对称轴的位置.
由于抛物线y=ax2+bx+c的对称轴是直线x=- ,故:
①b=0时,对称轴为y轴;
② >0(即a,b同号)时,对称轴在y轴左侧;
③ <0(即a,b异号)时,对称轴在y轴右侧.(3)c的大小决定抛物线y=ax2+bx+c与y轴交点的位置.
当x=0时,y=c,∴抛物线y=ax2+bx+c与y轴有且只有一个交点
(0,c).即:①c=0,抛物线经过原点;②c>0,与y轴交于正半轴;
③c<0,与y轴交于负半轴.
以上三点中,当结论和条件互换时,仍成立.1.(2014·巴中中考)已知二次函数y=ax2+bx+c的图象如图所示,则下列叙述正确的是 ( )
A.abc<0
B.-3a+c<0
C.b2-4ac≥0
D.将该函数图象向左平移2个单位后所得抛物线的表达式为y=ax2+c【解析】选B.A.由开口向下,可得a<0;又由抛物线与y轴交于负半轴,可得c<0,然后由对称轴在y轴右侧,得到b与a异号,则可得b>0,故得abc>0,故本选项错误;
B.根据图知对称轴为直线x=2,即- =2,得b=-4a,再根据图象知当x=1时,y=a+b+c=a-4a+c=-3a+c<0,故本选项正确;
C.由抛物线与x轴有两个交点,可得b2-4ac>0,故本选项错误;D.y=ax2+bx+c= ∵- =2,∴y=a(x-2)2
+ 向左平移2个单位后所得到抛物线的表达式为y=
ax2+ 故本选项错误;故选B.2.(2014·丽水中考)在同一平面直角坐标系内,将函数y=2x2
+4x-3的图象向右平移2个单位,再向下平移1个单位得到图象
的顶点坐标是 ( )
A.(-3,-6) B.(1,-4)
C.(1,-6) D.(-3,-4)
【解析】选C.y=2x2+4x-3=2(x+1)2-5,把y=2(x+1)2-5的图象向
右平移2个单位,再向下平移1个单位,
得y=2(x+1-2)2-5-1=2(x-1)2-6,
∴平移后的图象的顶点坐标是(1,-6).【知识归纳】二次函数的平移规律
平移不改变图形的形状和大小,因此抛物线在平移的过程中,图象的形状、开口方向必相同,即a不变,所以抛物线y=ax2+bx+c可以由y=ax2平移得到.其平移的规律用语言来表示可以归结为:“上加下减,左加右减”,平移时具体的对应关系可以用下列框图来表示:3.(2014·泰安中考)已知函数y=-(x-m)(x-n)
(其中m与反比例函数y= 的图象可能是 ( )【解析】选C.观察函数y=-(x-m)(x-n)(其中mn=1,m+n<0.所以一次函数y=mx+n的图象必过第二、四象限,且
与y轴交点为(0,1),反比例函数y= 的图象过第二、四象限.
所以选C.4.(2014·南宁中考)如图,已知二次函数y=-x2+2x,当-1A.a>1 B.-1C.a>0 D.-1∵-1∴a≤1,
∴-1【主题训练2】(2013·新疆中考)如图,已知
抛物线y=ax2+bx+3与x轴交于A,B两点,过点A
的直线l与抛物线交于点C,其中A点的坐标是
(1,0),C点坐标是(4,3).
(1)求抛物线的表达式.
(2)在(1)中抛物线的对称轴上是否存在点D,使△BCD的周长最小?若存在,求出点D的坐标,若不存在,请说明理由.【自主解答】(1)∵抛物线y=ax2+bx+3经过点A(1,0),点C(4,3),∴ 解得
所以抛物线的表达式为y=x2-4x+3.(2)∵点A,B关于对称轴对称,
∴点D为AC与对称轴的交点时△BCD的周长最小,
设直线AC的表达式为y=kx+b(k≠0),
则 解得
所以,直线AC的表达式为y=x-1,
∵y=x2-4x+3=(x-2)2-1,
∴抛物线的对称轴为直线x=2,
当x=2时,y=2-1=1,
∴抛物线对称轴上存在点D(2,1),使△BCD的周长最小. 【主题升华】选择不同表达形式求二次函数表达式的技巧
(1)当已知抛物线上任意三点时,通常设为一般式y=ax2+bx+c
(a≠0)的形式,然后组成三元一次方程组来求解.
(2)当已知抛物线的顶点或对称轴或最大(小)值时,通常设为顶
点式y=a(x-h)2+k(a≠0)的形式.
(3)当已知抛物线与x轴的交点(或交点横坐标)或已知抛物线与
x轴一个交点和对称轴时,通常设为交点式y=a(x-x1)·(x-x2)
(a≠0)的形式.1.(2013·营口中考)如图,抛物线与x轴交于A(1,0),B(-3,0)两点,与y轴交于点C(0,3),设抛物线的顶点为D.
(1)求该抛物线的表达式与顶点D的坐标.
(2)试判断△BCD的形状,并说明理由.【解析】(1)设抛物线的表达式为y=ax2+bx+c(a≠0).
由抛物线与y轴交于点C(0,3),可知c=3.即抛物线的表达式为y=ax2+bx+3.
把点A(1,0),点B(-3,0)代入,
得
解得a=-1,b=-2.
∴抛物线的表达式为y=-x2-2x+3.
∵y=-x2-2x+3=-(x+1)2+4,
∴顶点D的坐标为(-1,4).(2)△BCD是直角三角形.
理由如下:过点D分别作x轴、y轴的垂线,垂足分别为E,F.
∵在Rt△BOC中,OB=3,OC=3,
∴BC2=OB2+OC2=18.
在Rt△CDF中,DF=1,
CF=OF-OC=4-3=1,
∴CD2=DF2+CF2=2.在Rt△BDE中,DE=4,BE=OB-OE=3-1=2,
∴BD2=DE2+BE2=20,
∴BC2+CD2=BD2,
∴△BCD为直角三角形.【一题多解】本题中的第(2)问还可以这样求解:
过点D作DF⊥y轴于点F.
在Rt△BOC中,∵OB=3,OC=3,
∴OB=OC,∴∠OCB=45°.
∵在Rt△CDF中,DF=1,CF=OF-OC=4-3=1,
∴DF=CF,
∴∠DCF=45°,
∴∠BCD=180°-∠DCF-∠OCB=90°,
∴△BCD为直角三角形.2.(2014·黔东南中考)如图,直线y=x+2与抛物线y=ax2+bx
+6(a≠0)相交于A 和B(4,m),点P是线段AB上异于
A,B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
(1)求抛物线的表达式.
(2)是否存在这样的P点,使线段PC的长有
最大值,若存在,求出这个最大值;若不存
在,请说明理由.
(3)求△PAC为直角三角形时点P的坐标.【解析】(1)∵B(4,m)在直线y=x+2上,
∴m=4+2=6,
∴B(4,6),
∵A ,B(4,6)在抛物线y=ax2+bx+6上,
∴
∴a=2,b=-8,
∴y=2x2-8x+6.(2)存在P点,使线段PC的长有最大值.
设动点P的坐标为(n,n+2),
则C点的坐标为(n,2n2-8n+6),
∴PC=(n+2)-(2n2-8n+6)
=-2n2+9n-4
∵PC>0,∴当n= 时,线段PC最大且为 .(3)设直线AC的表达式为y=-x+p,
把A 代入得: =- +p,解得:p=3,
∴直线AC的表达式为y=-x+3,
点C在抛物线上,设C(t,2t2-8t+6),
代入y=-x+3得:2t2-8t+6=-t+3,
整理得:2t2-7t+3=0,
解得:t=3或t= ,
∴P(3,5)或 .
又∵P异于点A,B,∴点P的坐标为(3,5).主题3 二次函数的应用
【主题训练3】(2014·莆田中考)某水果店销售某种水果,由历年市场行情可知,从第1月至第12月,这种水果每千克售价y1(元)与销售时间第x月之间存在如图1(一条线段)的变化趋势,每千克成本y2(元)与销售时间第x月满足函数关系式y2=mx2-8mx+n,其变化趋势如图2.(1)求y2的表达式.
(2)第几月销售这种水果,每千克所获得利润最大?最大利润是多少?【自主解答】(1)由图可知,y2=mx2-8mx+n经过点(3,6),(7,7),
∴ 解得(2)设y1=kx+b(k≠0),
由图可知,函数图象经过点(4,11),(8,10),
则 解得
所以,y1=- x+12,
所以,每千克所获得利润∵- <0,
∴当x=3时,所获得利润最大,最大为 元.
答:第3月销售这种水果,每千克所获得利润最大,最大利润
是 元/千克.【主题升华】二次函数应用的类型及解题策略
(1)最值问题.
①利润最大问题的解题策略:先运用“总利润=总售价-总成本”或“总利润=单件商品利润×销售数量”建立利润与价格之间的二次函数表达式,再求出函数的最值.
②几何图形中最值问题的解题策略:先结合面积公式、相似等知识,把要讨论的量表示成另一变量的二次函数的形式,再求出函数的最值.(2)抛物线型问题.
解决此类实际问题的关键是进行二次函数建模,依据题意,建立合适的平面直角坐标系,并利用抛物线的性质解决问题.1.(2014·徐州中考)某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75.其图象如图所示.
(1)销售单价为多少元时,该种商品每天的销售利润最大?最大利润为多少元?
(2)销售单价在什么范围时,该种商品每天的销售利润不低于16元?【解析】(1)y=ax2+bx-75图象过点(5,0),(7,16),
∴ 解得
y=-x2+20x-75的顶点坐标是(10,25),
当x=10时,y最大=25.
答:销售单价为10元时,该种商品每天的销售利润最大,最大利润为25元.(2)∵函数y=-x2+20x-75图象的对称轴为直线x=10,
可知点(7,16)关于对称轴的对称点是(13,16),
又∵函数y=-x2+20x-75图象开口向下,
∴当7≤x≤13时,y≥16.
答:销售单价不少于7元且不超过13元时,该种商品每天的销售利润不低于16元.2.(2014·淮安中考)用长为32米的篱笆围一个矩形养鸡场,设围成的矩形一边长为x米,面积为y平方米.
(1)求y关于x的函数关系式.
(2)当x为何值时,围成的养鸡场面积为60平方米?
(3)能否围成面积为70平方米的养鸡场?如果能,请求出其边长;如果不能,请说明理由.【解析】(1)y=x(16-x)=-x2+16x(0(2)当y=60时,-x2+16x=60,解得x1=10,x2=6,
所以当x=10或6时,围成的养鸡场的面积为60平方米.
(3)方法一:当y=70时,-x2+16x=70,整理得:x2-16x+70=0,
由于Δ=256-280=-24<0,
因此此方程无实数根.
所以不能围成面积为70平方米的养鸡场.方法二:当y=70时,-x2+16x=70,整理得:x2-16x+70=0,
配方,得(x-8)2=-6,因此此方程无实数根,
所以不能围成面积为70平方米的养鸡场.3.(2014·西宁中考)今年5月1日起实施《青海省保障性住房准
入分配退出和运营管理实施细则》规定:公共租赁住房和廉租
住房并轨运行(以下简称并轨房),计划10年内解决低收入人群
住房问题.已知第x年(x为正整数)投入使用的并轨房面积为y百
万平方米,且y与x的函数关系式为y=- x+5.由于物价上涨等因
素的影响,每年单位面积租金也随之上调.假设每年的并轨房全
部出租完,预计第x年投入使用的并轨房的单位面积租金z与时
间x满足一次函数关系如下表:(1)求出z与x的函数关系式.
(2)设第x年政府投入使用的并轨房收取的租金为W百万元,请问政府在第几年投入使用的并轨房收取的租金最多,最多为多少百万元?【解析】(1)设z与x的一次函数关系为z=kx+b(k≠0),
∵x=1时,z=50,x=2时,z=52,
∴ 解得
∴z与x的函数关系式为z=2x+48.(2)由题意得,
W=yz= (2x+48)=
=- (x2-6x+9)+3+240=- (x-3)2+243,
∵- <0,∴当x=3时,W有最大值为243,
答:政府在第3年投入使用的并轨房收取的租金最多,最多为243百万元.【知识归纳】应用二次函数解决实际问题的基本思路
(1)理解问题.
(2)分析问题中的变量和常量以及它们之间的关系.
(3)用函数表达式表示它们之间的关系.
(4)计算或求解,并应用函数的性质作出判断.
(5)检验结果的合理性.
第 26 章主题1 二次函数的图象和性质
【主题训练1】(2014·安顺中考)如图,二次函数y=ax2+bx+c
(a>0)的图象的顶点为D,其图象与x轴的交点A,B的横坐标分别
为-1,3.与y轴负半轴交于点C.在下面五个结论中:
①2a-b=0;②a+b+c>0;③c=-3a;④只有当a= 时,△ABD是等腰
直角三角形;⑤使△ACB为等腰三角形的a的值可以有四个.其中
正确的结论是 .(只填序号)【解析】①∵函数图象与x轴的交点A,B的横坐标分别为-1,3,
∴对称轴为直线x=1,即:- =1,变形得:2a+b=0.
∴此结论错误;
②当x=1时,y=a+b+c<0,∴此结论错误;
③把(-1,0)和(3,0)代入表达式可得:
①×3+②得:12a+4c=0,即:c=-3a;
∴此结论正确;④当a= 时,由- =1可得b=-1;由a-b+c=0可得c=- ;
则D点的纵坐标为:
则D点到x轴的距离为2.连接AD,BD,∵顶点为点D,
∴AD=BD.又 AB=2,
可证△ABD是等腰直角三角形,
∴此结论正确;
⑤由上一步的结论可证此结论错误.
答案:③④【主题升华】系数a,b,c与二次函数的图象的关系
(1)a决定开口方向及开口大小.
当a>0时,开口向上,当a<0时,开口向下;|a|越大,抛物线的开口
越小.
(2)b和a共同决定抛物线对称轴的位置.
由于抛物线y=ax2+bx+c的对称轴是直线x=- ,故:
①b=0时,对称轴为y轴;
② >0(即a,b同号)时,对称轴在y轴左侧;
③ <0(即a,b异号)时,对称轴在y轴右侧.(3)c的大小决定抛物线y=ax2+bx+c与y轴交点的位置.
当x=0时,y=c,∴抛物线y=ax2+bx+c与y轴有且只有一个交点
(0,c).即:①c=0,抛物线经过原点;②c>0,与y轴交于正半轴;
③c<0,与y轴交于负半轴.
以上三点中,当结论和条件互换时,仍成立.1.(2014·巴中中考)已知二次函数y=ax2+bx+c的图象如图所示,则下列叙述正确的是 ( )
A.abc<0
B.-3a+c<0
C.b2-4ac≥0
D.将该函数图象向左平移2个单位后所得抛物线的表达式为y=ax2+c【解析】选B.A.由开口向下,可得a<0;又由抛物线与y轴交于负半轴,可得c<0,然后由对称轴在y轴右侧,得到b与a异号,则可得b>0,故得abc>0,故本选项错误;
B.根据图知对称轴为直线x=2,即- =2,得b=-4a,再根据图象知当x=1时,y=a+b+c=a-4a+c=-3a+c<0,故本选项正确;
C.由抛物线与x轴有两个交点,可得b2-4ac>0,故本选项错误;D.y=ax2+bx+c= ∵- =2,∴y=a(x-2)2
+ 向左平移2个单位后所得到抛物线的表达式为y=
ax2+ 故本选项错误;故选B.2.(2014·丽水中考)在同一平面直角坐标系内,将函数y=2x2
+4x-3的图象向右平移2个单位,再向下平移1个单位得到图象
的顶点坐标是 ( )
A.(-3,-6) B.(1,-4)
C.(1,-6) D.(-3,-4)
【解析】选C.y=2x2+4x-3=2(x+1)2-5,把y=2(x+1)2-5的图象向
右平移2个单位,再向下平移1个单位,
得y=2(x+1-2)2-5-1=2(x-1)2-6,
∴平移后的图象的顶点坐标是(1,-6).【知识归纳】二次函数的平移规律
平移不改变图形的形状和大小,因此抛物线在平移的过程中,图象的形状、开口方向必相同,即a不变,所以抛物线y=ax2+bx+c可以由y=ax2平移得到.其平移的规律用语言来表示可以归结为:“上加下减,左加右减”,平移时具体的对应关系可以用下列框图来表示:3.(2014·泰安中考)已知函数y=-(x-m)(x-n)
(其中m
与y轴交点为(0,1),反比例函数y= 的图象过第二、四象限.
所以选C.4.(2014·南宁中考)如图,已知二次函数y=-x2+2x,当-1
∴-1
抛物线y=ax2+bx+3与x轴交于A,B两点,过点A
的直线l与抛物线交于点C,其中A点的坐标是
(1,0),C点坐标是(4,3).
(1)求抛物线的表达式.
(2)在(1)中抛物线的对称轴上是否存在点D,使△BCD的周长最小?若存在,求出点D的坐标,若不存在,请说明理由.【自主解答】(1)∵抛物线y=ax2+bx+3经过点A(1,0),点C(4,3),∴ 解得
所以抛物线的表达式为y=x2-4x+3.(2)∵点A,B关于对称轴对称,
∴点D为AC与对称轴的交点时△BCD的周长最小,
设直线AC的表达式为y=kx+b(k≠0),
则 解得
所以,直线AC的表达式为y=x-1,
∵y=x2-4x+3=(x-2)2-1,
∴抛物线的对称轴为直线x=2,
当x=2时,y=2-1=1,
∴抛物线对称轴上存在点D(2,1),使△BCD的周长最小. 【主题升华】选择不同表达形式求二次函数表达式的技巧
(1)当已知抛物线上任意三点时,通常设为一般式y=ax2+bx+c
(a≠0)的形式,然后组成三元一次方程组来求解.
(2)当已知抛物线的顶点或对称轴或最大(小)值时,通常设为顶
点式y=a(x-h)2+k(a≠0)的形式.
(3)当已知抛物线与x轴的交点(或交点横坐标)或已知抛物线与
x轴一个交点和对称轴时,通常设为交点式y=a(x-x1)·(x-x2)
(a≠0)的形式.1.(2013·营口中考)如图,抛物线与x轴交于A(1,0),B(-3,0)两点,与y轴交于点C(0,3),设抛物线的顶点为D.
(1)求该抛物线的表达式与顶点D的坐标.
(2)试判断△BCD的形状,并说明理由.【解析】(1)设抛物线的表达式为y=ax2+bx+c(a≠0).
由抛物线与y轴交于点C(0,3),可知c=3.即抛物线的表达式为y=ax2+bx+3.
把点A(1,0),点B(-3,0)代入,
得
解得a=-1,b=-2.
∴抛物线的表达式为y=-x2-2x+3.
∵y=-x2-2x+3=-(x+1)2+4,
∴顶点D的坐标为(-1,4).(2)△BCD是直角三角形.
理由如下:过点D分别作x轴、y轴的垂线,垂足分别为E,F.
∵在Rt△BOC中,OB=3,OC=3,
∴BC2=OB2+OC2=18.
在Rt△CDF中,DF=1,
CF=OF-OC=4-3=1,
∴CD2=DF2+CF2=2.在Rt△BDE中,DE=4,BE=OB-OE=3-1=2,
∴BD2=DE2+BE2=20,
∴BC2+CD2=BD2,
∴△BCD为直角三角形.【一题多解】本题中的第(2)问还可以这样求解:
过点D作DF⊥y轴于点F.
在Rt△BOC中,∵OB=3,OC=3,
∴OB=OC,∴∠OCB=45°.
∵在Rt△CDF中,DF=1,CF=OF-OC=4-3=1,
∴DF=CF,
∴∠DCF=45°,
∴∠BCD=180°-∠DCF-∠OCB=90°,
∴△BCD为直角三角形.2.(2014·黔东南中考)如图,直线y=x+2与抛物线y=ax2+bx
+6(a≠0)相交于A 和B(4,m),点P是线段AB上异于
A,B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
(1)求抛物线的表达式.
(2)是否存在这样的P点,使线段PC的长有
最大值,若存在,求出这个最大值;若不存
在,请说明理由.
(3)求△PAC为直角三角形时点P的坐标.【解析】(1)∵B(4,m)在直线y=x+2上,
∴m=4+2=6,
∴B(4,6),
∵A ,B(4,6)在抛物线y=ax2+bx+6上,
∴
∴a=2,b=-8,
∴y=2x2-8x+6.(2)存在P点,使线段PC的长有最大值.
设动点P的坐标为(n,n+2),
则C点的坐标为(n,2n2-8n+6),
∴PC=(n+2)-(2n2-8n+6)
=-2n2+9n-4
∵PC>0,∴当n= 时,线段PC最大且为 .(3)设直线AC的表达式为y=-x+p,
把A 代入得: =- +p,解得:p=3,
∴直线AC的表达式为y=-x+3,
点C在抛物线上,设C(t,2t2-8t+6),
代入y=-x+3得:2t2-8t+6=-t+3,
整理得:2t2-7t+3=0,
解得:t=3或t= ,
∴P(3,5)或 .
又∵P异于点A,B,∴点P的坐标为(3,5).主题3 二次函数的应用
【主题训练3】(2014·莆田中考)某水果店销售某种水果,由历年市场行情可知,从第1月至第12月,这种水果每千克售价y1(元)与销售时间第x月之间存在如图1(一条线段)的变化趋势,每千克成本y2(元)与销售时间第x月满足函数关系式y2=mx2-8mx+n,其变化趋势如图2.(1)求y2的表达式.
(2)第几月销售这种水果,每千克所获得利润最大?最大利润是多少?【自主解答】(1)由图可知,y2=mx2-8mx+n经过点(3,6),(7,7),
∴ 解得(2)设y1=kx+b(k≠0),
由图可知,函数图象经过点(4,11),(8,10),
则 解得
所以,y1=- x+12,
所以,每千克所获得利润∵- <0,
∴当x=3时,所获得利润最大,最大为 元.
答:第3月销售这种水果,每千克所获得利润最大,最大利润
是 元/千克.【主题升华】二次函数应用的类型及解题策略
(1)最值问题.
①利润最大问题的解题策略:先运用“总利润=总售价-总成本”或“总利润=单件商品利润×销售数量”建立利润与价格之间的二次函数表达式,再求出函数的最值.
②几何图形中最值问题的解题策略:先结合面积公式、相似等知识,把要讨论的量表示成另一变量的二次函数的形式,再求出函数的最值.(2)抛物线型问题.
解决此类实际问题的关键是进行二次函数建模,依据题意,建立合适的平面直角坐标系,并利用抛物线的性质解决问题.1.(2014·徐州中考)某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75.其图象如图所示.
(1)销售单价为多少元时,该种商品每天的销售利润最大?最大利润为多少元?
(2)销售单价在什么范围时,该种商品每天的销售利润不低于16元?【解析】(1)y=ax2+bx-75图象过点(5,0),(7,16),
∴ 解得
y=-x2+20x-75的顶点坐标是(10,25),
当x=10时,y最大=25.
答:销售单价为10元时,该种商品每天的销售利润最大,最大利润为25元.(2)∵函数y=-x2+20x-75图象的对称轴为直线x=10,
可知点(7,16)关于对称轴的对称点是(13,16),
又∵函数y=-x2+20x-75图象开口向下,
∴当7≤x≤13时,y≥16.
答:销售单价不少于7元且不超过13元时,该种商品每天的销售利润不低于16元.2.(2014·淮安中考)用长为32米的篱笆围一个矩形养鸡场,设围成的矩形一边长为x米,面积为y平方米.
(1)求y关于x的函数关系式.
(2)当x为何值时,围成的养鸡场面积为60平方米?
(3)能否围成面积为70平方米的养鸡场?如果能,请求出其边长;如果不能,请说明理由.【解析】(1)y=x(16-x)=-x2+16x(0
所以当x=10或6时,围成的养鸡场的面积为60平方米.
(3)方法一:当y=70时,-x2+16x=70,整理得:x2-16x+70=0,
由于Δ=256-280=-24<0,
因此此方程无实数根.
所以不能围成面积为70平方米的养鸡场.方法二:当y=70时,-x2+16x=70,整理得:x2-16x+70=0,
配方,得(x-8)2=-6,因此此方程无实数根,
所以不能围成面积为70平方米的养鸡场.3.(2014·西宁中考)今年5月1日起实施《青海省保障性住房准
入分配退出和运营管理实施细则》规定:公共租赁住房和廉租
住房并轨运行(以下简称并轨房),计划10年内解决低收入人群
住房问题.已知第x年(x为正整数)投入使用的并轨房面积为y百
万平方米,且y与x的函数关系式为y=- x+5.由于物价上涨等因
素的影响,每年单位面积租金也随之上调.假设每年的并轨房全
部出租完,预计第x年投入使用的并轨房的单位面积租金z与时
间x满足一次函数关系如下表:(1)求出z与x的函数关系式.
(2)设第x年政府投入使用的并轨房收取的租金为W百万元,请问政府在第几年投入使用的并轨房收取的租金最多,最多为多少百万元?【解析】(1)设z与x的一次函数关系为z=kx+b(k≠0),
∵x=1时,z=50,x=2时,z=52,
∴ 解得
∴z与x的函数关系式为z=2x+48.(2)由题意得,
W=yz= (2x+48)=
=- (x2-6x+9)+3+240=- (x-3)2+243,
∵- <0,∴当x=3时,W有最大值为243,
答:政府在第3年投入使用的并轨房收取的租金最多,最多为243百万元.【知识归纳】应用二次函数解决实际问题的基本思路
(1)理解问题.
(2)分析问题中的变量和常量以及它们之间的关系.
(3)用函数表达式表示它们之间的关系.
(4)计算或求解,并应用函数的性质作出判断.
(5)检验结果的合理性.
