人教版数学六年级下册《圆锥的体积》课件
文档属性
| 名称 | 人教版数学六年级下册《圆锥的体积》课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-09 21:45:19 | ||
图片预览






文档简介
(共32张PPT)
公式推导
知识运用
巩固练习
拓展练习
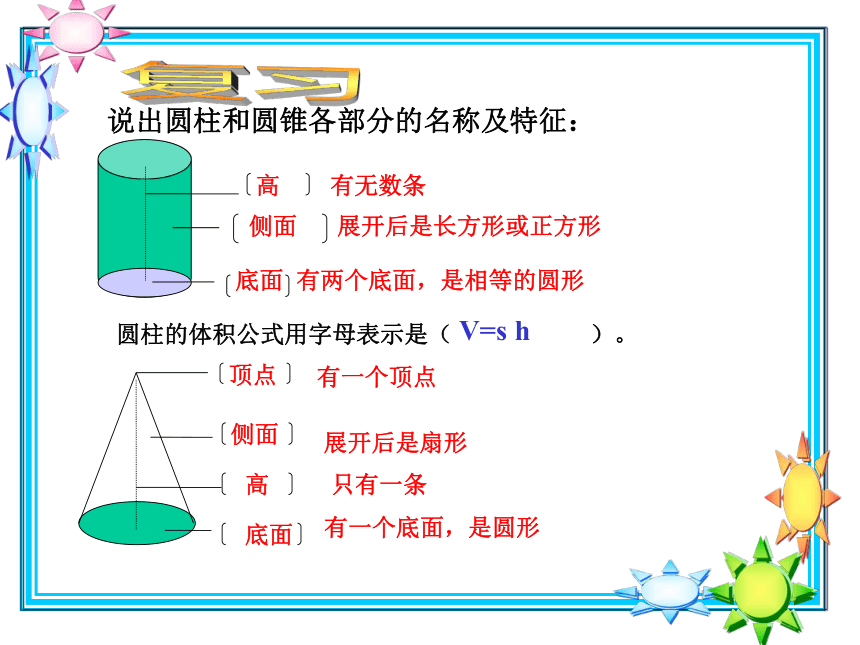
说出圆柱和圆锥各部分的名称及特征:
高
有无数条
侧面
展开后是长方形或正方形
底面
有两个底面,是相等的圆形
顶点
有一个顶点
侧面
展开后是扇形
高
只有一条
有一个底面,是圆形
圆柱的体积公式用字母表示是( )。
V=s h
底面
异同点
1、说一说圆锥有哪些特征?
(1)顶部:尖顶;
(2)底面:是一个圆;
(3)侧面:是一个曲面(展开是一个扇形);
(4)底面圆周上任一点与顶点之间的距离都相等。
(5)高只有一条。
2、同桌说一说圆柱体积的计算公式。
(1)已知 s、h 求 v=
(2)已知 r、h 求 v=
(3)已知 d、h 求 v
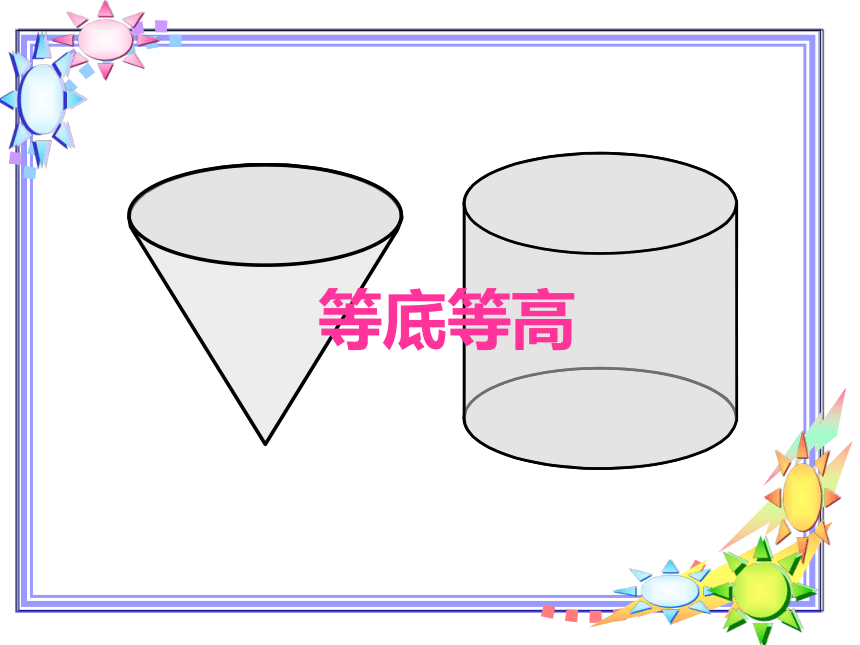
等底等高
等底等高
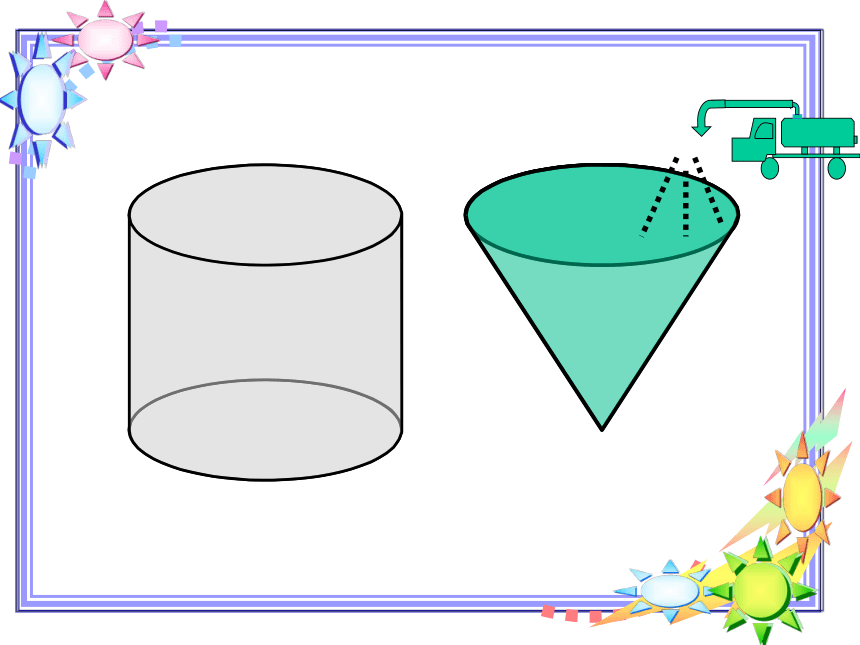
实验报告表
实验器材
一桶水、等底等高
的圆柱和圆锥各一个
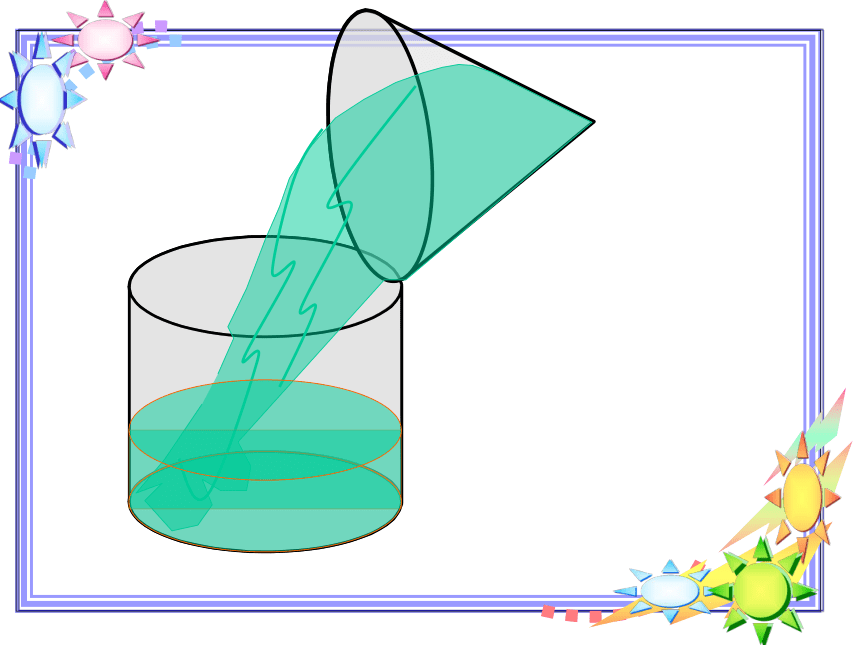
实验过程
①在空圆柱里满水倒入空圆锥里,( )次正好倒完。
在空圆锥里装 满水倒入空圆柱里,( )次正好装满。
结 论
②圆柱的体积是和它( )的圆锥体积的( )倍。
圆锥体积
计算公式
V=
②圆锥的体积是和它( )
的圆柱体积的
实 验 报 告 表
3
3
等底等高
等底等高
3
3
1
3
1
S h
圆柱体积=底面积 高
1
3
圆锥体积=底面积 高
Ⅴ= S × h
1
3
圆锥的体积V等于和它等底等高的圆柱体积的三分之一
V= sh
1
3
V圆柱=sh
思考
要求圆锥的体积,必须知道
哪两个条件?为什么要乘
3
1
一个圆锥形零件,底面积是19平方厘米,高是12厘米,这个零件的体积是多少?
V= sh
1
3
×19×12=76(立方厘米)
1
3
答:这个零件的体积是76立方厘米。
试一试:一个圆锥形的零件,底面积是170平方厘米,高是12厘米。这个零件的体积是多少?
答:这个零件的体积是680立方厘米。
×170 ×12=
680(立方厘米)
第一步:求沙堆底面积
每二步:求沙堆的体积
1、工地上有一些沙子,堆起来近似于一个圆锥,这堆沙子大约多少立方米 (得数保留两位小数.)
4m
1.2m
沙堆底面积:3.14×( )
=3.14×4
=12.56(㎡)
4
2
2
沙堆的体积: ×12.56×1.2
=5.024(m )
≈5.02(m )
1
3
3
3
答:这堆沙子大约有5.02立方米.
4m
1.2m
1、已知圆锥的底面半径r和高h,如 何求体积V?
2、已知圆锥的底面直径d和高h,如何求体积V?
3、已知圆锥的底面周长C和高h,如何求体积V?
r= d÷2
S=∏
V= S h
S=∏
V= S h
r =C÷∏÷2
S=∏
V= S h
一个圆锥体铅锤高6dm,底面半径4dm,这个铅锤的体积是多少立方分米?
×3.14×42×6
=32×3.14
=100.48(dm2)
答:这个铅锤的体积是100.48dm2。
已 知 条 件 体积
圆锥底面半径2厘米,高9厘米
圆锥底面直径6厘米,高3厘米
圆锥底面周长6.28分米,高6分米
37.68立方厘米
28.26立方厘米
6.28立方分米
1、如图把圆柱形铅笔削成圆锥形,削去部分的体积是圆柱体积的( ) (1)三分之一 (2)三分之二 (3)无法确定
问:圆锥体积、削去部分的体积与圆柱体积之间的比是( ): ( ) : ( )
2
2
1
3
1、削成的圆锥体与圆柱体等底等高,所以削成的圆锥体积是圆柱体积的三分之一,那么削去的体积就是圆柱体的三分之二。或者削去的体积是圆锥的2倍
2、等底等高时,V锥:V柱=1:3
讨论:以下圆柱体积与圆锥体积之间有什么关系?
1、底面积相等,圆锥的高是圆柱高的3倍
2、底面积相等,圆柱的高是圆锥高的3倍
3、高相等,圆柱底面积是圆锥底面积的3倍
4、高相等,圆锥底面半径是圆柱底面半径的3倍
圆锥体积等于圆柱体积
圆柱的体积是圆锥体积的9倍
圆柱的体积是圆锥体积的9倍
圆锥的体积是圆柱体积的3倍
思 考:
1、一个圆锥与一个圆柱等底等高,
已知圆锥的体积是 18 立方米,
圆柱的体积是( )。
2、一个圆锥与一个圆柱等底等体积,
已知圆柱的高是 12 厘米, 圆锥的
高是( )。
3、一个圆锥与一个圆柱等高等体积,
已知圆柱的底面积是 314 平方米,
圆锥的底面积是( )。
54 立方米
36 厘米
942 平方米
把一个长9.42分米、宽5分米、高2分米的长方体铁块熔铸成一个底面半径是3分米的圆锥,圆锥的高是多少分米?
=94.2(立方分米)
=28.26(立方分米)
①长方体体积:
9.42×5×2
②圆锥的底面积:
2
3.14×3
=94.2 ÷ 9.42
=10(分米)
③圆锥的高:
94.2×3 ÷ 28.26
通过本节课的学习,
你有什么收获
公式推导
知识运用
巩固练习
拓展练习
说出圆柱和圆锥各部分的名称及特征:
高
有无数条
侧面
展开后是长方形或正方形
底面
有两个底面,是相等的圆形
顶点
有一个顶点
侧面
展开后是扇形
高
只有一条
有一个底面,是圆形
圆柱的体积公式用字母表示是( )。
V=s h
底面
异同点
1、说一说圆锥有哪些特征?
(1)顶部:尖顶;
(2)底面:是一个圆;
(3)侧面:是一个曲面(展开是一个扇形);
(4)底面圆周上任一点与顶点之间的距离都相等。
(5)高只有一条。
2、同桌说一说圆柱体积的计算公式。
(1)已知 s、h 求 v=
(2)已知 r、h 求 v=
(3)已知 d、h 求 v
等底等高
等底等高
实验报告表
实验器材
一桶水、等底等高
的圆柱和圆锥各一个
实验过程
①在空圆柱里满水倒入空圆锥里,( )次正好倒完。
在空圆锥里装 满水倒入空圆柱里,( )次正好装满。
结 论
②圆柱的体积是和它( )的圆锥体积的( )倍。
圆锥体积
计算公式
V=
②圆锥的体积是和它( )
的圆柱体积的
实 验 报 告 表
3
3
等底等高
等底等高
3
3
1
3
1
S h
圆柱体积=底面积 高
1
3
圆锥体积=底面积 高
Ⅴ= S × h
1
3
圆锥的体积V等于和它等底等高的圆柱体积的三分之一
V= sh
1
3
V圆柱=sh
思考
要求圆锥的体积,必须知道
哪两个条件?为什么要乘
3
1
一个圆锥形零件,底面积是19平方厘米,高是12厘米,这个零件的体积是多少?
V= sh
1
3
×19×12=76(立方厘米)
1
3
答:这个零件的体积是76立方厘米。
试一试:一个圆锥形的零件,底面积是170平方厘米,高是12厘米。这个零件的体积是多少?
答:这个零件的体积是680立方厘米。
×170 ×12=
680(立方厘米)
第一步:求沙堆底面积
每二步:求沙堆的体积
1、工地上有一些沙子,堆起来近似于一个圆锥,这堆沙子大约多少立方米 (得数保留两位小数.)
4m
1.2m
沙堆底面积:3.14×( )
=3.14×4
=12.56(㎡)
4
2
2
沙堆的体积: ×12.56×1.2
=5.024(m )
≈5.02(m )
1
3
3
3
答:这堆沙子大约有5.02立方米.
4m
1.2m
1、已知圆锥的底面半径r和高h,如 何求体积V?
2、已知圆锥的底面直径d和高h,如何求体积V?
3、已知圆锥的底面周长C和高h,如何求体积V?
r= d÷2
S=∏
V= S h
S=∏
V= S h
r =C÷∏÷2
S=∏
V= S h
一个圆锥体铅锤高6dm,底面半径4dm,这个铅锤的体积是多少立方分米?
×3.14×42×6
=32×3.14
=100.48(dm2)
答:这个铅锤的体积是100.48dm2。
已 知 条 件 体积
圆锥底面半径2厘米,高9厘米
圆锥底面直径6厘米,高3厘米
圆锥底面周长6.28分米,高6分米
37.68立方厘米
28.26立方厘米
6.28立方分米
1、如图把圆柱形铅笔削成圆锥形,削去部分的体积是圆柱体积的( ) (1)三分之一 (2)三分之二 (3)无法确定
问:圆锥体积、削去部分的体积与圆柱体积之间的比是( ): ( ) : ( )
2
2
1
3
1、削成的圆锥体与圆柱体等底等高,所以削成的圆锥体积是圆柱体积的三分之一,那么削去的体积就是圆柱体的三分之二。或者削去的体积是圆锥的2倍
2、等底等高时,V锥:V柱=1:3
讨论:以下圆柱体积与圆锥体积之间有什么关系?
1、底面积相等,圆锥的高是圆柱高的3倍
2、底面积相等,圆柱的高是圆锥高的3倍
3、高相等,圆柱底面积是圆锥底面积的3倍
4、高相等,圆锥底面半径是圆柱底面半径的3倍
圆锥体积等于圆柱体积
圆柱的体积是圆锥体积的9倍
圆柱的体积是圆锥体积的9倍
圆锥的体积是圆柱体积的3倍
思 考:
1、一个圆锥与一个圆柱等底等高,
已知圆锥的体积是 18 立方米,
圆柱的体积是( )。
2、一个圆锥与一个圆柱等底等体积,
已知圆柱的高是 12 厘米, 圆锥的
高是( )。
3、一个圆锥与一个圆柱等高等体积,
已知圆柱的底面积是 314 平方米,
圆锥的底面积是( )。
54 立方米
36 厘米
942 平方米
把一个长9.42分米、宽5分米、高2分米的长方体铁块熔铸成一个底面半径是3分米的圆锥,圆锥的高是多少分米?
=94.2(立方分米)
=28.26(立方分米)
①长方体体积:
9.42×5×2
②圆锥的底面积:
2
3.14×3
=94.2 ÷ 9.42
=10(分米)
③圆锥的高:
94.2×3 ÷ 28.26
通过本节课的学习,
你有什么收获
