物理人教版(2019)必修第一册4.5牛顿运动定律的应用——板块模型(共25张ppt)
文档属性
| 名称 | 物理人教版(2019)必修第一册4.5牛顿运动定律的应用——板块模型(共25张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 688.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-01-10 11:41:02 | ||
图片预览







文档简介
(共25张PPT)
板-块模型
学习目标及重点
1.能说出“板-块”模型的概念。
2.能掌握“板-块”模型的分析方法。(重点)
3.能运用牛顿运动定律处理“板-块”问题。(重点)
板-块模型的概念
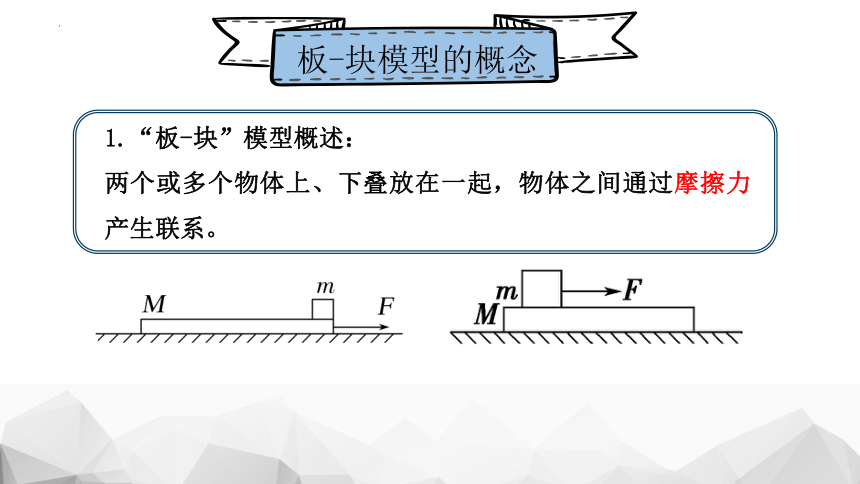
1.“板-块”模型概述:
两个或多个物体上、下叠放在一起,物体之间通过摩擦力产生联系。
板-块模型的分析方法
1.“滑块—木板”模型的三个基本关系
加速度的关系 注意:通过受力分析判断加速度是否相同 加速度相同 用“整体法”求出它们一起运动的加速度
加速度不相同 用“隔离法”分别求出滑块与木板的加速度
速度的关系 速度相同的过程中 ①都做匀速运动时,无摩擦 ②都做变速时,存在静摩擦力 注意:当速度刚相等的瞬间,摩擦力会发生突变
速度不相同的过程中 滑块与木板之间存在滑动摩擦力 位移的关系 无相对位移(速度相等的过程中) 速度保持相同 注意:计算过程中的速度,位移,都是相对于地面而言。
有相对位移(速度不相等的过程中) ①速度方向相同, x相对=x木板+x滑块 ②速度方向不相同,x相对=x木板-x滑块 2.“滑块—木板”模型的解题方法和步骤
(1)明确各物体对地的运动和物体间的相对运动情况,确定物体间的摩擦力种类和方向。
(2)通过受力分析,求出各物体在各个运动过程中的加速度。
(3)根据物理量之间的关系列式计算。
注意:①此类问题涉及两个物体、多个运动过程。
②前一个过程的末速度是下一个过程的初速度。
③不同运动过程转变的瞬间,加速度可能突变,需重新受力分析
1.地面光滑的“滑块—木板”问题
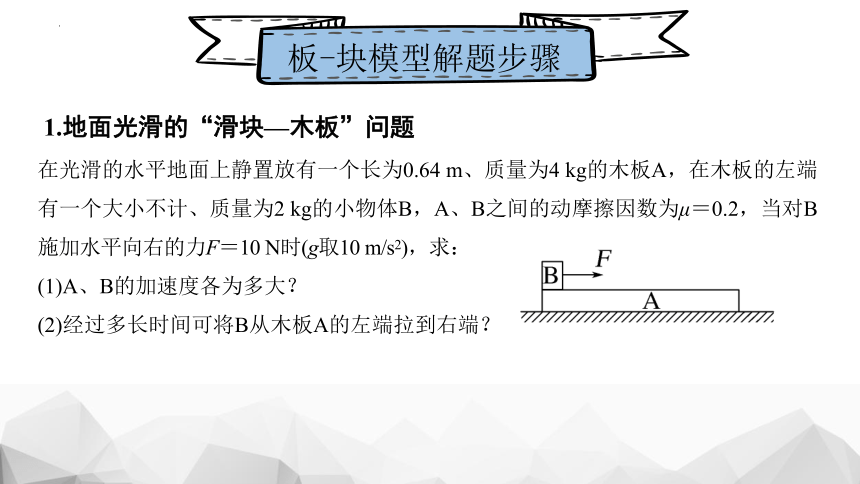
在光滑的水平地面上静置放有一个长为0.64 m、质量为4 kg的木板A,在木板的左端有一个大小不计、质量为2 kg的小物体B,A、B之间的动摩擦因数为μ=0.2,当对B施加水平向右的力F=10 N时(g取10 m/s2),求:
(1)A、B的加速度各为多大?
(2)经过多长时间可将B从木板A的左端拉到右端?
板-块模型解题步骤
(1)A、B间的滑动摩擦力的大小为:f滑==4(N)
以B为研究对象,根据牛顿第二定律得:,解得:aB=3m/s2
以A为研究对象,根据牛顿第二定律得:f滑=mAaA,解得:aB=1m/s2
(2)设将B从A的左端拉到右端所用时间为t,A、B在这段时间内发生的位移分别为xA和xB,其关系如图所示:
xB-xA=L
,
解得t=0.8s
1.(多选)如图所示,质量为M=1 kg足够长的木板静止在光滑水平面上,质量m=0.5 kg的滑块(可视为质点)以v0=3 m/s的初速度从左端沿木板上表面冲上木板,带动木板向前滑动,已知滑块与木板间的动摩擦因数μ=0.1,重力加速度g取10 m/s2,则( )
A.滑块的加速度大小为1 m/s2
B.木板的加速度大小为1 m/s2
C.滑块和木板达到共同速度的时间为2 s
D.滑块和木板达到共同速度时,滑块相对木板滑动的位移大小为3 m
典例
ACD
如图所示,厚度不计的薄板A长L=5 m,质量M=5 kg,放在水平地面上。在A上距右端x=3 m处放一物体B(大小不计),其质量m=2 kg,已知A、B间的动摩擦因数μ1=0.1,A与地面间的动摩擦因数μ2=0.2,原来系统静止.现在板的右端施加一大小恒定的水平力F=26 N,持续作用在A上,将A从B下抽出.取g=10 m/s2,求:
(1)A从B下抽出前A、B的加速度各是多大;
(2)B运动多长时间离开A。
(3)B离开A时的速度的大小。
2.地面光滑的“滑块—木板”问题
(1)对B受力分析,由牛顿第二定律可得:μ1mg=maB,解得:aB=1 m/s2
对A受力分析,由牛顿第二定律可得:F-μ1mg-μ2(m+M)g=MaA
解得:aA=2 m/s2。
(2)设经时间t,A从B下抽出。根据位移关系:xA-xB=L-x
,,解得:t=2s
(3)B离开A时的速度大小为vB=aBt=2 m/s。
2.如图所示,质量为M=1 kg的长木板静止在光滑水平面上,现有一质量为m=0.5 kg的小滑块(可视为质点)以v0=3 m/s 的初速度从左端沿木板上表面冲上木板,带动木板向前滑动.已知滑块与木板上表面间的动摩擦因数μ=0.1,重力加速度g取10 m/s2,木板足够长.求:
(1)滑块在木板上滑动过程中,长木板受到的摩擦力大小和方向;
(2)滑块在木板上滑动过程中,滑块相对于地面的加速度a的大小;
(3)滑块与木板A达到的共同速度v的大小.
典例
(1)滑块所受摩擦力为滑动摩擦力:f滑=μmg=0.5 N,方向向左
根据牛顿第三定律,滑块对木板的摩擦力方向向右,大小为0.5 N.
(2)由牛顿第二定律得:μmg=ma,得a滑块=μg=1 m/s2。
(3)木板的加速度:=0.5 m/s2
设经过时间t,滑块和长木板达到共同速度v,则满足:
对滑块:v=v0-a滑块t, 对长木板:v=a木板t
由以上两式得滑块和长木板达到的共同速度:v=1 m/s.
典例
3.(多选)如图所示,A、B两物块的质量分别为1 kg和2 kg,静止叠放在水平地面上,A、B间的动摩擦因数为0.4,B与地面间的动摩擦因数为0.2,最大静摩擦力近似等于滑动摩擦力,重力加速度g=10 m/s2。现对B施加一水平拉力F=12 N,则( )
A.B对A摩擦力大小为4 N
B.B对A摩擦力大小为2 N
C.A、B发生相对滑动,A的加速度为4 m/s2
D.A、B一起做匀加速运动,加速度为2 m/s2
BD
4.如图所示,质量为m的木块在质量为M的长木板上受到水平向右的拉力F的作用向右滑行,但长木板保持静止不动.已知木块与长木板之间的动摩擦因数为μ1,长木板与地面之间的动摩擦因数为μ2,下列说法正确的是 ( )
A.长木板受到地面的摩擦力的大小一定为μ1Mg
B.长木板受到地面的摩擦力的大小一定为μ2(m+M)g
C.只要拉力F增大到足够大,长木板一定会与地面发生相对滑动
D.无论拉力F增加到多大,长木板都不会与地面发生相对滑动
典例
D
5. (多选)如图所示,上表面粗糙的平板小车静止于光滑水平面上。t=0时,小车以初速度v0向右运动,将小滑块无初速度地放置于小车的右端,最终小滑块恰好没有滑出小车。如图乙所示为小滑块与小车运动的v-t图像,图中t1、v0、v1均为已知量,重力加速度大小取g。由此可求得( )
A.小车的长度
B.小滑块的质量
C.小车在匀减速运动过程中的加速度
D.小滑块与小车之间的动摩擦因数
典例
ACD
6.质量为m0=20 kg、长为L=5 m的木板放在水平地面上,木板与水平地面间的动摩擦因数为μ1=0.15。质量为m=10 kg的小铁块(可视为质点),以v0=4 m/s的速度从木板的左端水平冲上木板(如图所示),小铁块与木板间的动摩擦因数为μ2=0.4(最大静摩擦力等于滑动摩擦力,g=10 m/s2)。则下列判断正确的是( )
A.木板一定静止不动,小铁块不能滑出木板
B.木板一定静止不动,小铁块能滑出木板
C.木板一定向右滑动,小铁块不能滑出木板
D.木板一定向右滑动,小铁块能滑出木板
A
典例
木板与地面间的最大静摩擦力为f1=μ1(m0+m)g=45 N,小铁块与木板之间的最大静摩擦力为f2=μ2mg=40 N,因f1>f2,所以木板一定静止不动;假设小铁块未滑出木板,在木板上滑行的距离为x,则v02=2μ2gx,解得x=2 m<L=5 m,所以小铁块不能滑出木板,故A正确。
7.如图所示,物块A、木板B的质量分别为mA=5 kg,mB=10 kg,不计物块A的大小,木板B长L=4 m。开始时A、B均静止。现使A以水平初速度v0从B的最左端开始运动。已知A与B之间的动摩擦因数为0.3,水平地面光滑,g取10 m/s2。
(1)求物块A和木板B发生相对运动过程的加速度的大小;
(2)若A刚好没有从B上滑下来,求A的初速度v0的大小。
典例
(1)对A受力分析,加速度大小:aA=μg=3 m/s2
对B受力分析,加速度大小:aB==1.5 m/s2。
(2)由题意可知,A刚好没有从B上滑下来,A滑到B最右端时的速度和B的速度相同,则有:v=v0-a1t,v=a2t
由位移关系得:,解得:v0=6m/s
8. 如图,质量M=1 kg、长L=4 m的木板静止在粗糙的水平地面上,木板与地面间的动摩擦因数μ1=0.1,在木板的左端放置质量m=1 kg,大小可以忽略的铁块,铁块与木板之间的动摩擦因数μ2=0.4,某时刻起在铁块上施加一个水平向右的恒力F=8 N,g取10 m/s2。
(1)求施加恒力F后铁块和木板的加速度大小;
(2)铁块经多长时间到达木板的最右端,求此时木板的速度;
(3)当铁块运动到木板最右端时,把铁块拿走,木板还能滑行的距离。
典例
(1)研究铁块,根据牛顿第二定律得:F-μ2mg=ma1,解得:a1=4 m/s2
研究木板,根据牛顿第二定律得: μ2mg-μ1(M+m)g=Ma2,
解得a2=2 m/s2。
(2)设铁块运动到木板的最右端时间为t,根据位移关系:x铁块-x木板=L,
,,解得:t=2s,所以:v木板=a2t=4 m/s
(3)拿走铁块后木板做匀减速运动,加速度大小为:a3=μ1g=1 m/s2
则木板还能继续滑行的距离x=,解得:x=8m
总结
01
“板-块模型”的三个关系:
1.加速度关系:通过受力分析,利用牛顿第二定律
2.速度关系:判断有无相对位移
2.位移关系:理解相对位移
02
2.“板-块”模型的解题方法和步骤:
(1)明确各物体运动状况
(2)受力分析,求出加速度。
(3)根据物理量之间的关系列式计算。
THANK YOU
板-块模型
学习目标及重点
1.能说出“板-块”模型的概念。
2.能掌握“板-块”模型的分析方法。(重点)
3.能运用牛顿运动定律处理“板-块”问题。(重点)
板-块模型的概念
1.“板-块”模型概述:
两个或多个物体上、下叠放在一起,物体之间通过摩擦力产生联系。
板-块模型的分析方法
1.“滑块—木板”模型的三个基本关系
加速度的关系 注意:通过受力分析判断加速度是否相同 加速度相同 用“整体法”求出它们一起运动的加速度
加速度不相同 用“隔离法”分别求出滑块与木板的加速度
速度的关系 速度相同的过程中 ①都做匀速运动时,无摩擦 ②都做变速时,存在静摩擦力 注意:当速度刚相等的瞬间,摩擦力会发生突变
速度不相同的过程中 滑块与木板之间存在滑动摩擦力 位移的关系 无相对位移(速度相等的过程中) 速度保持相同 注意:计算过程中的速度,位移,都是相对于地面而言。
有相对位移(速度不相等的过程中) ①速度方向相同, x相对=x木板+x滑块 ②速度方向不相同,x相对=x木板-x滑块 2.“滑块—木板”模型的解题方法和步骤
(1)明确各物体对地的运动和物体间的相对运动情况,确定物体间的摩擦力种类和方向。
(2)通过受力分析,求出各物体在各个运动过程中的加速度。
(3)根据物理量之间的关系列式计算。
注意:①此类问题涉及两个物体、多个运动过程。
②前一个过程的末速度是下一个过程的初速度。
③不同运动过程转变的瞬间,加速度可能突变,需重新受力分析
1.地面光滑的“滑块—木板”问题
在光滑的水平地面上静置放有一个长为0.64 m、质量为4 kg的木板A,在木板的左端有一个大小不计、质量为2 kg的小物体B,A、B之间的动摩擦因数为μ=0.2,当对B施加水平向右的力F=10 N时(g取10 m/s2),求:
(1)A、B的加速度各为多大?
(2)经过多长时间可将B从木板A的左端拉到右端?
板-块模型解题步骤
(1)A、B间的滑动摩擦力的大小为:f滑==4(N)
以B为研究对象,根据牛顿第二定律得:,解得:aB=3m/s2
以A为研究对象,根据牛顿第二定律得:f滑=mAaA,解得:aB=1m/s2
(2)设将B从A的左端拉到右端所用时间为t,A、B在这段时间内发生的位移分别为xA和xB,其关系如图所示:
xB-xA=L
,
解得t=0.8s
1.(多选)如图所示,质量为M=1 kg足够长的木板静止在光滑水平面上,质量m=0.5 kg的滑块(可视为质点)以v0=3 m/s的初速度从左端沿木板上表面冲上木板,带动木板向前滑动,已知滑块与木板间的动摩擦因数μ=0.1,重力加速度g取10 m/s2,则( )
A.滑块的加速度大小为1 m/s2
B.木板的加速度大小为1 m/s2
C.滑块和木板达到共同速度的时间为2 s
D.滑块和木板达到共同速度时,滑块相对木板滑动的位移大小为3 m
典例
ACD
如图所示,厚度不计的薄板A长L=5 m,质量M=5 kg,放在水平地面上。在A上距右端x=3 m处放一物体B(大小不计),其质量m=2 kg,已知A、B间的动摩擦因数μ1=0.1,A与地面间的动摩擦因数μ2=0.2,原来系统静止.现在板的右端施加一大小恒定的水平力F=26 N,持续作用在A上,将A从B下抽出.取g=10 m/s2,求:
(1)A从B下抽出前A、B的加速度各是多大;
(2)B运动多长时间离开A。
(3)B离开A时的速度的大小。
2.地面光滑的“滑块—木板”问题
(1)对B受力分析,由牛顿第二定律可得:μ1mg=maB,解得:aB=1 m/s2
对A受力分析,由牛顿第二定律可得:F-μ1mg-μ2(m+M)g=MaA
解得:aA=2 m/s2。
(2)设经时间t,A从B下抽出。根据位移关系:xA-xB=L-x
,,解得:t=2s
(3)B离开A时的速度大小为vB=aBt=2 m/s。
2.如图所示,质量为M=1 kg的长木板静止在光滑水平面上,现有一质量为m=0.5 kg的小滑块(可视为质点)以v0=3 m/s 的初速度从左端沿木板上表面冲上木板,带动木板向前滑动.已知滑块与木板上表面间的动摩擦因数μ=0.1,重力加速度g取10 m/s2,木板足够长.求:
(1)滑块在木板上滑动过程中,长木板受到的摩擦力大小和方向;
(2)滑块在木板上滑动过程中,滑块相对于地面的加速度a的大小;
(3)滑块与木板A达到的共同速度v的大小.
典例
(1)滑块所受摩擦力为滑动摩擦力:f滑=μmg=0.5 N,方向向左
根据牛顿第三定律,滑块对木板的摩擦力方向向右,大小为0.5 N.
(2)由牛顿第二定律得:μmg=ma,得a滑块=μg=1 m/s2。
(3)木板的加速度:=0.5 m/s2
设经过时间t,滑块和长木板达到共同速度v,则满足:
对滑块:v=v0-a滑块t, 对长木板:v=a木板t
由以上两式得滑块和长木板达到的共同速度:v=1 m/s.
典例
3.(多选)如图所示,A、B两物块的质量分别为1 kg和2 kg,静止叠放在水平地面上,A、B间的动摩擦因数为0.4,B与地面间的动摩擦因数为0.2,最大静摩擦力近似等于滑动摩擦力,重力加速度g=10 m/s2。现对B施加一水平拉力F=12 N,则( )
A.B对A摩擦力大小为4 N
B.B对A摩擦力大小为2 N
C.A、B发生相对滑动,A的加速度为4 m/s2
D.A、B一起做匀加速运动,加速度为2 m/s2
BD
4.如图所示,质量为m的木块在质量为M的长木板上受到水平向右的拉力F的作用向右滑行,但长木板保持静止不动.已知木块与长木板之间的动摩擦因数为μ1,长木板与地面之间的动摩擦因数为μ2,下列说法正确的是 ( )
A.长木板受到地面的摩擦力的大小一定为μ1Mg
B.长木板受到地面的摩擦力的大小一定为μ2(m+M)g
C.只要拉力F增大到足够大,长木板一定会与地面发生相对滑动
D.无论拉力F增加到多大,长木板都不会与地面发生相对滑动
典例
D
5. (多选)如图所示,上表面粗糙的平板小车静止于光滑水平面上。t=0时,小车以初速度v0向右运动,将小滑块无初速度地放置于小车的右端,最终小滑块恰好没有滑出小车。如图乙所示为小滑块与小车运动的v-t图像,图中t1、v0、v1均为已知量,重力加速度大小取g。由此可求得( )
A.小车的长度
B.小滑块的质量
C.小车在匀减速运动过程中的加速度
D.小滑块与小车之间的动摩擦因数
典例
ACD
6.质量为m0=20 kg、长为L=5 m的木板放在水平地面上,木板与水平地面间的动摩擦因数为μ1=0.15。质量为m=10 kg的小铁块(可视为质点),以v0=4 m/s的速度从木板的左端水平冲上木板(如图所示),小铁块与木板间的动摩擦因数为μ2=0.4(最大静摩擦力等于滑动摩擦力,g=10 m/s2)。则下列判断正确的是( )
A.木板一定静止不动,小铁块不能滑出木板
B.木板一定静止不动,小铁块能滑出木板
C.木板一定向右滑动,小铁块不能滑出木板
D.木板一定向右滑动,小铁块能滑出木板
A
典例
木板与地面间的最大静摩擦力为f1=μ1(m0+m)g=45 N,小铁块与木板之间的最大静摩擦力为f2=μ2mg=40 N,因f1>f2,所以木板一定静止不动;假设小铁块未滑出木板,在木板上滑行的距离为x,则v02=2μ2gx,解得x=2 m<L=5 m,所以小铁块不能滑出木板,故A正确。
7.如图所示,物块A、木板B的质量分别为mA=5 kg,mB=10 kg,不计物块A的大小,木板B长L=4 m。开始时A、B均静止。现使A以水平初速度v0从B的最左端开始运动。已知A与B之间的动摩擦因数为0.3,水平地面光滑,g取10 m/s2。
(1)求物块A和木板B发生相对运动过程的加速度的大小;
(2)若A刚好没有从B上滑下来,求A的初速度v0的大小。
典例
(1)对A受力分析,加速度大小:aA=μg=3 m/s2
对B受力分析,加速度大小:aB==1.5 m/s2。
(2)由题意可知,A刚好没有从B上滑下来,A滑到B最右端时的速度和B的速度相同,则有:v=v0-a1t,v=a2t
由位移关系得:,解得:v0=6m/s
8. 如图,质量M=1 kg、长L=4 m的木板静止在粗糙的水平地面上,木板与地面间的动摩擦因数μ1=0.1,在木板的左端放置质量m=1 kg,大小可以忽略的铁块,铁块与木板之间的动摩擦因数μ2=0.4,某时刻起在铁块上施加一个水平向右的恒力F=8 N,g取10 m/s2。
(1)求施加恒力F后铁块和木板的加速度大小;
(2)铁块经多长时间到达木板的最右端,求此时木板的速度;
(3)当铁块运动到木板最右端时,把铁块拿走,木板还能滑行的距离。
典例
(1)研究铁块,根据牛顿第二定律得:F-μ2mg=ma1,解得:a1=4 m/s2
研究木板,根据牛顿第二定律得: μ2mg-μ1(M+m)g=Ma2,
解得a2=2 m/s2。
(2)设铁块运动到木板的最右端时间为t,根据位移关系:x铁块-x木板=L,
,,解得:t=2s,所以:v木板=a2t=4 m/s
(3)拿走铁块后木板做匀减速运动,加速度大小为:a3=μ1g=1 m/s2
则木板还能继续滑行的距离x=,解得:x=8m
总结
01
“板-块模型”的三个关系:
1.加速度关系:通过受力分析,利用牛顿第二定律
2.速度关系:判断有无相对位移
2.位移关系:理解相对位移
02
2.“板-块”模型的解题方法和步骤:
(1)明确各物体运动状况
(2)受力分析,求出加速度。
(3)根据物理量之间的关系列式计算。
THANK YOU
