中位数与众数

课件15张PPT。8.2中位数与众数重点、难点及关键教学重点：理解众数、中位数的
意义及他们的求法.
教学难点：求特殊情况下的众数
和中位数.
教学关键：准确地将一组数据进
行整理，按顺序排列.
复习与回顾平均数是表示一组数据的“平均水平”；
如果一个公司的员工的平均工资是２０００元，那么是不是每个人的工资就是２０００元？
如果一个公司的员工的平均工资是２０００
元，那么是不是一定一半员工的工资比２０００
元多，另一半员工的工资比２０００元少？
如果一个公司的员工的平均工资是２０００元，那么是不是大多数员工的工资是２０００元左右？例 某公司员工的月工资如下：经理说：我公司员工收入很高,月平均工资是2000元。职员C说：我的工资是1200元，在公司算是中等。职员D说：我们好几个人的工资都是1100元。问题：他们的说法都对吗？你认为哪个数据最能表示该公司员工的“平均水平”？6000元，4000元，1700元，1300元，1200元，1100元，1100元，1100元，500元.n个数据按大小顺序排列，处于最中间位置的一个数据（或最中间两个数据的平均数）叫做这组数据的中位数（median）一组数据中出现次数最多的那个数据叫做这组数据的众数（mode）.
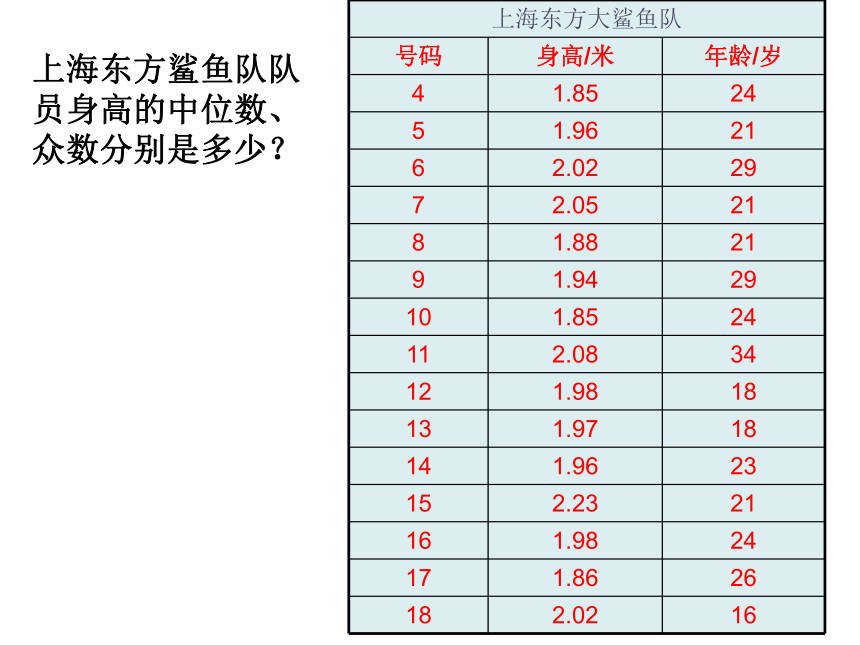
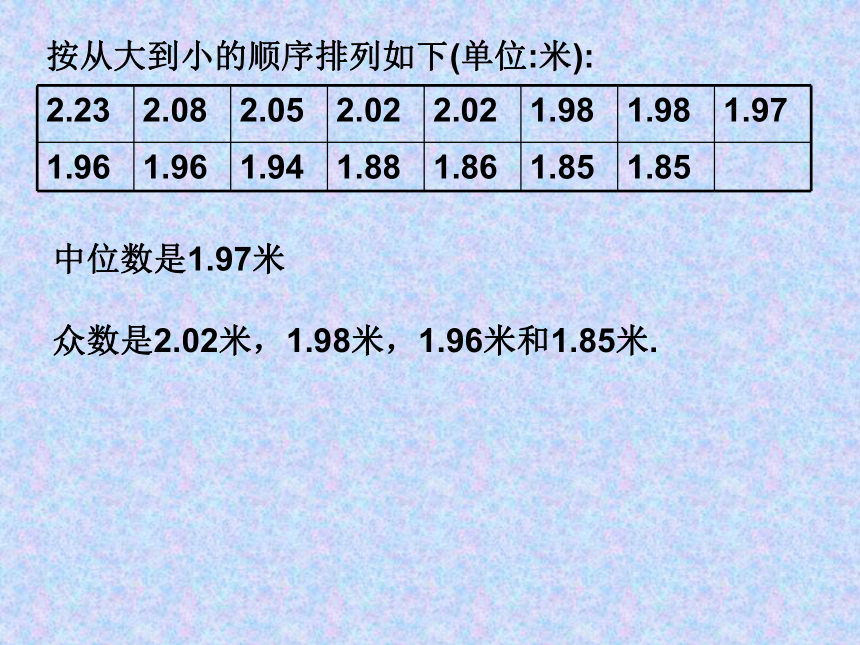
上海东方鲨鱼队队员身高的中位数、众数分别是多少？中位数是1.97米众数是2.02米，1.98米，1.96米和1.85米.按从大到小的顺序排列如下(单位:米):例 某公司员工的月工资如下：问题：为什么这个问题中的平均数比中位数与众数要高得多？议一议：平均数、中位数和众数有哪些特征？想一想:上面说的这些特征在实际生活中有哪些地方用到?1、在一次英语口试中，20名学生的得分如下：
80 100 60 80 70 90 50 80 70
80 70 90 80 90 80 70 90 60 80
求这次英语口试中学生得分的众数。15 17 14 10 15 19 17 16 14 12求这一天10名工人生产的零件的中位数. 2：10名工人某天生产同一零件，
生产的件数是
学校要召开运动会，决定从初三年级的八个班中抽调男生64人组成彩旗方队，如果从初三（1）班的体检表中抽出了10份男生表格，得到10名男生的身高（单位：米）如下：
1.63 1.60 1.68 1.66 1.66 1.70 1.75 1.66 1.58 1.65
根据这10个身高值提供的信息，试确定参加方队的学生的最佳身高值.练习题一： 某公司销售部有营销人员15人，销售部为了制定
某种商品的月销售额，统计了这15人某月的销售量
如下表： （1）求这15位营销员该月销售量的平均数、中
位数和众数。 （2）假设销售部负责人把每位营销员的月销售额
定为320件，你认为是否合理，为什么？如果不合理，
请你制定一个较为合理的销售定额，并说明理由。某公司员工的月工资情况统计如下表：（1）分别计算该公司月工资的平均数，中位数和众数。（2）你认为用（1）中计算出的哪个数据来代表该公司
员工的月工资水平更为合适？请简要说明理由。（3）请画出一种你认为合适的统计图来表示上边表格中
的数据。