第二十四章 圆 复习课(第2课时)课件(共15张PPT)2023-2024学年人教版九年级数学上册
文档属性
| 名称 | 第二十四章 圆 复习课(第2课时)课件(共15张PPT)2023-2024学年人教版九年级数学上册 |
|
|
| 格式 | pptx | ||
| 文件大小 | 765.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-11 11:41:53 | ||
图片预览





文档简介
(共15张PPT)
第二十四章 圆
复习课(第2课时)
复习目标
专题复习
课堂小结
课后训练
复习目标
1.通过复习与圆有关的位置关系,熟练掌握点、直线与圆的位置关系,并且能够证明相关问题。
2.通过复习切线的性质与判定、切线长与切线长定理熟练掌握相关的证明题目,总结出证明题中辅助线的画法。
3.通过复习三角形的外接圆与内切圆,熟练掌握相关的证明题目。
专题一 点和圆的位置关系
知识回顾
如果圆的半径是r,点到圆心的距离是d.
点在圆外
点在圆上
点在圆内
d>r
d=r
d·
·
O
r
d
注意:判断点与圆的位置关系主要是根据d与r的大小关系判断
例题1.如图,在矩形ABCD中AB=8,AD=6,
若以A为圆心,10为半径作⊙O,则A、
B、C、D四个点有几个点在⊙O内部?
A
D
C
B
解:由题意知
点B到圆心的距离为AB=8,圆的半径r=10,d点C到圆心的距离为AC=10,圆的半径r=10,d=r,点B在圆上,
点D到圆心的距离为AD=6,圆的半径r=10,d由此可知点A、点B、点D这三个点在圆内。
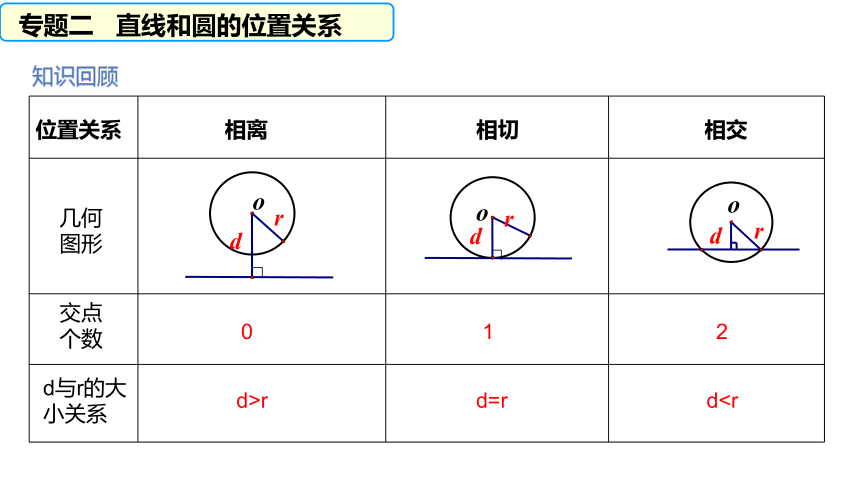
专题二 直线和圆的位置关系
知识回顾
∟
r
d
o
∟
r
d
o
r
d
o
位置关系
相离
相切
相交
几何图形
交点个数
d与r的大小关系
0
1
2
d>r
d=r
d例题2.如图,在直角三角形ABC中,∠C=90°,AB=5,cosA=,以点B为圆心,r为半径作⊙B,当r=3时,⊙B与AC的位置关系是什么?
C
B
A
解:由题意知
AC=AB×cosA = 4
由勾股定理可得BC=3
因为BC垂直于AC
所以BC的长度就是圆心B到直线AC的距离
因为BC=r
所以⊙B与AC相切
专题三 切线的性质与判定
知识回顾
切线的性质:
圆的切线垂直于过切点的半径
切线的判定:
①和圆只有一个公共点的直线是圆的切线
②如果圆心到一条直线的距离等于圆的半径,那么这条直线是圆的切线
③经过半径的外端并且垂直于这条半径的直线是圆的切线
证明圆的切线的技巧:
①有公共点,连半径,证垂直;
②无公共点,作垂直,证半径。
例题3(有公共点,连半径,作垂直).如图,AB是⊙O的直径,C、D都是⊙O上的点,AD平分∠CAB,过点D作AC的垂线,交AC的延长线于点E,交AB的延长线于点F。
求证:EF是⊙O的切线。
·
F
E
D
C
B
A
O
解:连接OD
∵D是⊙O上的点 ∴OD是⊙O的半径
∵AD平分∠CAB
∴∠CAD=∠BAD
∵∠DOB=2∠BAD(同弧所对的圆周角是圆心角的一半)
∴∠DOB=∠CAD+∠BAD=∠CAB
∴AE//OD
∴∠ODB=∠AED=90°
∴EF是⊙O的切线
例题4(无公共点,作垂直,证半径).如图,在三角形ABC中,∠ACB=90°,D是AB边的中点,点O在AC边上,⊙O经过点C且与AB边相切于点E,∠FAC=∠BDC。
求证:AF是⊙O的切线。
·
E
D
C
B
A
O
证明:连接OE,作OM垂直于AF垂足为M
∵D是AB中点
∴DC=AB=AD
∴∠DAC=∠DCA
∴∠BDC=2∠DAC
∵∠FAC=∠BDC
∴∠FAC=∠DAC
F
M
∵AB是⊙O的切线,切点为E
∴ ∠AEO=90°
在Rt△AOE与 Rt△AOM中
∵∠OEA=∠OMA
∠EAO=∠MAO
AO=AO
∴Rt△AOE≌ Rt△AOM
∴OM=OE
∴AF是⊙O的切线
专题四 切线长与切线长定理
知识回顾
切线长:
经过圆外一点的圆的切线上,这点和切点之间线段的长,叫做这点到圆的切线长。
切线长定理:
从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角。
例题5.
专题五 三角形的外接圆与内切圆
外接圆 内切圆
图形
定义
圆心O
性质
知识回顾
经过三角形三个顶点的圆
与三角形各边都相切的圆
外心:三角形三边中垂直平分线的交点
内心:三角形三条角平分线的交点
A
B
O
A
B
C
O
1.OA=OB=OC
2.外心在三角形内部、三角形边上、三角形外部都有可能.
1.到三边的距离相等;
2.OA、OB、OC分别平分∠BAC、∠ABC、∠ACB
3.内心在三角形内部.
△ABC的内切圆⊙O与三边分别切于D、E、F三点,如图,已知AF=3,BD+CE=12,则△ABC的周长是 .
30
A
B
C
F
E
D
O
直角三角形的两直角边分别是3cm ,4cm,试问:
(1)它的外接圆半径是 cm;内切圆半径是 cm?
·
A
B
C
E
D
F
O
2.5
1
解:如图,△ABC的外接圆直径为AB,而由勾股定理可得AB=5cm,故外接圆半径为2.5cm.连接AO,BO,CO.设△ABC的内接圆半径为r,由面积公式可得:S△ABC=S△AoB+S△AoC+S△BoC ,即 ,所以 ,代入数据得r=1cm.
方法小结:直角三角形的外接圆半径等于斜边长的一半,内接圆半径 .
拓展提升
谢谢!
第二十四章 圆
复习课(第2课时)
复习目标
专题复习
课堂小结
课后训练
复习目标
1.通过复习与圆有关的位置关系,熟练掌握点、直线与圆的位置关系,并且能够证明相关问题。
2.通过复习切线的性质与判定、切线长与切线长定理熟练掌握相关的证明题目,总结出证明题中辅助线的画法。
3.通过复习三角形的外接圆与内切圆,熟练掌握相关的证明题目。
专题一 点和圆的位置关系
知识回顾
如果圆的半径是r,点到圆心的距离是d.
点在圆外
点在圆上
点在圆内
d>r
d=r
d
·
O
r
d
注意:判断点与圆的位置关系主要是根据d与r的大小关系判断
例题1.如图,在矩形ABCD中AB=8,AD=6,
若以A为圆心,10为半径作⊙O,则A、
B、C、D四个点有几个点在⊙O内部?
A
D
C
B
解:由题意知
点B到圆心的距离为AB=8,圆的半径r=10,d
点D到圆心的距离为AD=6,圆的半径r=10,d
专题二 直线和圆的位置关系
知识回顾
∟
r
d
o
∟
r
d
o
r
d
o
位置关系
相离
相切
相交
几何图形
交点个数
d与r的大小关系
0
1
2
d>r
d=r
d
C
B
A
解:由题意知
AC=AB×cosA = 4
由勾股定理可得BC=3
因为BC垂直于AC
所以BC的长度就是圆心B到直线AC的距离
因为BC=r
所以⊙B与AC相切
专题三 切线的性质与判定
知识回顾
切线的性质:
圆的切线垂直于过切点的半径
切线的判定:
①和圆只有一个公共点的直线是圆的切线
②如果圆心到一条直线的距离等于圆的半径,那么这条直线是圆的切线
③经过半径的外端并且垂直于这条半径的直线是圆的切线
证明圆的切线的技巧:
①有公共点,连半径,证垂直;
②无公共点,作垂直,证半径。
例题3(有公共点,连半径,作垂直).如图,AB是⊙O的直径,C、D都是⊙O上的点,AD平分∠CAB,过点D作AC的垂线,交AC的延长线于点E,交AB的延长线于点F。
求证:EF是⊙O的切线。
·
F
E
D
C
B
A
O
解:连接OD
∵D是⊙O上的点 ∴OD是⊙O的半径
∵AD平分∠CAB
∴∠CAD=∠BAD
∵∠DOB=2∠BAD(同弧所对的圆周角是圆心角的一半)
∴∠DOB=∠CAD+∠BAD=∠CAB
∴AE//OD
∴∠ODB=∠AED=90°
∴EF是⊙O的切线
例题4(无公共点,作垂直,证半径).如图,在三角形ABC中,∠ACB=90°,D是AB边的中点,点O在AC边上,⊙O经过点C且与AB边相切于点E,∠FAC=∠BDC。
求证:AF是⊙O的切线。
·
E
D
C
B
A
O
证明:连接OE,作OM垂直于AF垂足为M
∵D是AB中点
∴DC=AB=AD
∴∠DAC=∠DCA
∴∠BDC=2∠DAC
∵∠FAC=∠BDC
∴∠FAC=∠DAC
F
M
∵AB是⊙O的切线,切点为E
∴ ∠AEO=90°
在Rt△AOE与 Rt△AOM中
∵∠OEA=∠OMA
∠EAO=∠MAO
AO=AO
∴Rt△AOE≌ Rt△AOM
∴OM=OE
∴AF是⊙O的切线
专题四 切线长与切线长定理
知识回顾
切线长:
经过圆外一点的圆的切线上,这点和切点之间线段的长,叫做这点到圆的切线长。
切线长定理:
从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角。
例题5.
专题五 三角形的外接圆与内切圆
外接圆 内切圆
图形
定义
圆心O
性质
知识回顾
经过三角形三个顶点的圆
与三角形各边都相切的圆
外心:三角形三边中垂直平分线的交点
内心:三角形三条角平分线的交点
A
B
O
A
B
C
O
1.OA=OB=OC
2.外心在三角形内部、三角形边上、三角形外部都有可能.
1.到三边的距离相等;
2.OA、OB、OC分别平分∠BAC、∠ABC、∠ACB
3.内心在三角形内部.
△ABC的内切圆⊙O与三边分别切于D、E、F三点,如图,已知AF=3,BD+CE=12,则△ABC的周长是 .
30
A
B
C
F
E
D
O
直角三角形的两直角边分别是3cm ,4cm,试问:
(1)它的外接圆半径是 cm;内切圆半径是 cm?
·
A
B
C
E
D
F
O
2.5
1
解:如图,△ABC的外接圆直径为AB,而由勾股定理可得AB=5cm,故外接圆半径为2.5cm.连接AO,BO,CO.设△ABC的内接圆半径为r,由面积公式可得:S△ABC=S△AoB+S△AoC+S△BoC ,即 ,所以 ,代入数据得r=1cm.
方法小结:直角三角形的外接圆半径等于斜边长的一半,内接圆半径 .
拓展提升
谢谢!
同课章节目录
