-五年级下册数学苏教版7.1解决问题的策略课件(共23张PPT)
文档属性
| 名称 | -五年级下册数学苏教版7.1解决问题的策略课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 9.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-11 13:31:56 | ||
图片预览






文档简介
(共23张PPT)
七 解决问题的策略
用转化的策略解决问题(1)
苏教版五年级下册数学
1.经历用转化策略解决问题的过程,体会用转化策略解决问题的基本思考方法和特点,能根据具体问题确定合理的解题思路,从而有效地解决问题。
2.通过对解决问题过程的回顾、比较和反思,进一步体会转化策略的内在价值,增强解决问题的策略意识,提高从不同角度分析和研究问题的能力。
学习目标
我们曾经运用转化的策略解决过哪些问题?
课堂导入
我们曾经运用转化的策略解决过哪些问题?
课堂导入
1
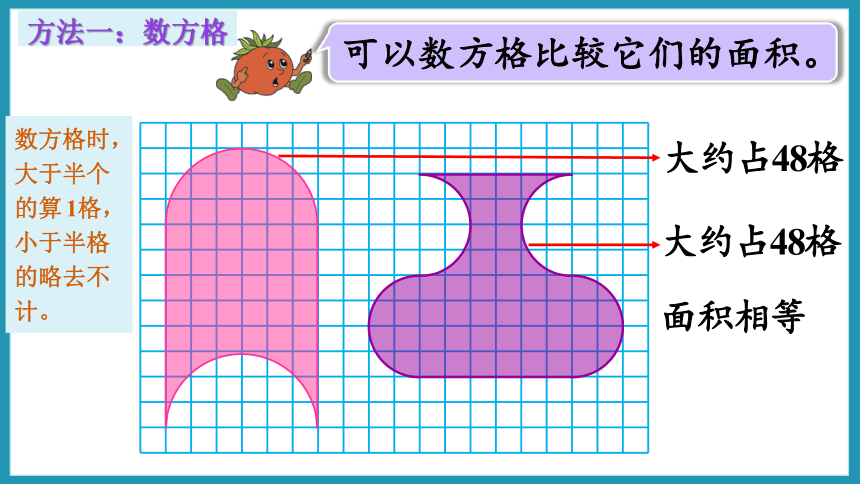
下面两个图形,哪个面积大一些?
怎样比较呢?
探究新知
可以数方格比较它们的面积。
大约占48格
大约占48格
面积相等
方法一:数方格
数方格时,大于半个的算1格,小于半格的略去不计。
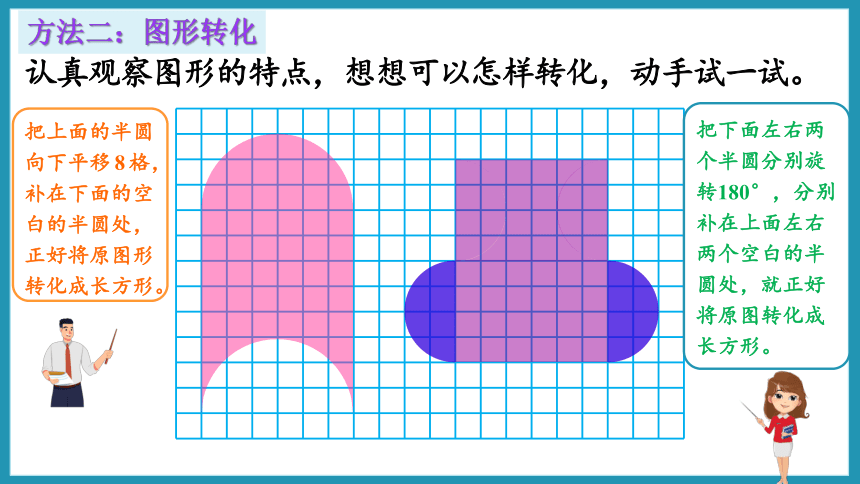
认真观察图形的特点,想想可以怎样转化,动手试一试。
方法二:图形转化
把上面的半圆向下平移8格,补在下面的空白的半圆处,正好将原图形转化成长方形。
把下面左右两个半圆分别旋转180°,分别补在上面左右两个空白的半圆处,就正好将原图转化成长方形。
运用了什么策略?
转化
规则
不规则
将什么转化成了什么?
运用了什么方法?
平移、旋转
转化前后的图形,什么变了什么没变?
形状变了,
大小没变。
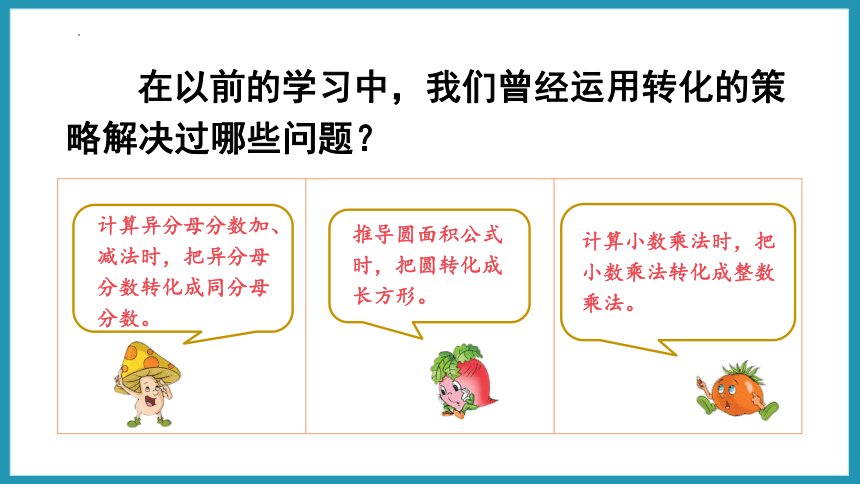
在以前的学习中,我们曾经运用转化的策略解决过哪些问题?
计算异分母分数加、减法时,把异分母分数转化成同分母分数。
推导圆面积公式时,把圆转化成长方形。
计算小数乘法时,把小数乘法转化成整数乘法。
计算异分母分数加减法时,把异分母分数转化成同分母分数。
0.12
0.3
×
0.036
12
3
×
36
扩大100倍
扩大10倍
缩小到它的 倍
计算小数乘法时,把小数乘法转化成整数乘法。
转化
未知 →
→ 已知
将什么转化成什么?
转化
复杂 →
→ 简单
推导圆面积公式时, 把圆转化成长方形。
将什么转化成什么?
1.明明和冬冬在同样大小的长方形纸上分别画了一个图案(图中直条的宽度都相等)。 这两个图案的面积相等吗? 为什么?
相等
课堂练习
2.用分数表示下面图形的阴影部分。
8
1
2
1
4
1
4
1
2
1
2
1
3. 你能求出下面各图中涂色部分的周长吗
6×4+3.14×6=42.84(cm)
15×2+3.14×25÷2+25=94.25(cm)
4.如图是程辛在美术课上设计的一幅花瓶图案,这幅图案的周
长和面积分别是多少?(小方格的边长是1厘米)
周长:4×2+3.14×2×2=20.56(厘米)
面积:4×4=16(平方厘米)
答:这幅图案的周长是20.56厘米,面积是16平方厘
米。
5.如图,在一块长方形地中有一条宽为2米的水泥路,则这
条水泥路的面积是多少平方米?
2×10=20(平方米)
答:这条水泥路的面积是20平方米。
6. 求下面各图中涂色部分的面积。(单位:厘米)
第一幅图:8×8=64(平方厘米)
第二幅图:10÷2÷2=2.5(厘米)
3.14×2.52×2=39.25(平方厘米)
提升练习
7. 如图,OA、OB分别为小半圆的直径,且OA=OB=6厘米,∠BOA=90°。涂色部分的面积为多少平方厘米
6×6÷2=18(平方厘米)
[提示]如图,连接AB、OC,将①移到③处,将②移到④处,涂色部分面积即为三角形AOB的面积。
8. 把一个长10厘米、宽4厘米的长方形按如图的方法折叠,涂色部分两个三角形的周长之和是多少厘米
10×2+4×2=28(厘米)
1. 如图正方形中两个涂色长方形的周长和是60厘米,求正方形的面积。
60÷4=15(厘米)
15×15=225(平方厘米)
[提示]两个长方形的周长和等于正方形的周长。先求出正方形的边长,再求面积。
思维拓展
2.如图所示,两个圆的半径都是2厘米,且图中粉色和蓝色
部分的面积相等。EF的长度是多少厘米?
3.14×22÷2=6.28(平方厘米)
6.28÷2=3.14(厘米)
2×2-3.14=0.86(厘米)
答:EF的长度是0.86厘米。
在计算不规则图形的面积和周长时,通常要对不规则图形进行平移或旋转,使之变成已知的或较简单的图形后再进行计算。
课堂小结
这节课你有什么收获?
七 解决问题的策略
用转化的策略解决问题(1)
苏教版五年级下册数学
1.经历用转化策略解决问题的过程,体会用转化策略解决问题的基本思考方法和特点,能根据具体问题确定合理的解题思路,从而有效地解决问题。
2.通过对解决问题过程的回顾、比较和反思,进一步体会转化策略的内在价值,增强解决问题的策略意识,提高从不同角度分析和研究问题的能力。
学习目标
我们曾经运用转化的策略解决过哪些问题?
课堂导入
我们曾经运用转化的策略解决过哪些问题?
课堂导入
1
下面两个图形,哪个面积大一些?
怎样比较呢?
探究新知
可以数方格比较它们的面积。
大约占48格
大约占48格
面积相等
方法一:数方格
数方格时,大于半个的算1格,小于半格的略去不计。
认真观察图形的特点,想想可以怎样转化,动手试一试。
方法二:图形转化
把上面的半圆向下平移8格,补在下面的空白的半圆处,正好将原图形转化成长方形。
把下面左右两个半圆分别旋转180°,分别补在上面左右两个空白的半圆处,就正好将原图转化成长方形。
运用了什么策略?
转化
规则
不规则
将什么转化成了什么?
运用了什么方法?
平移、旋转
转化前后的图形,什么变了什么没变?
形状变了,
大小没变。
在以前的学习中,我们曾经运用转化的策略解决过哪些问题?
计算异分母分数加、减法时,把异分母分数转化成同分母分数。
推导圆面积公式时,把圆转化成长方形。
计算小数乘法时,把小数乘法转化成整数乘法。
计算异分母分数加减法时,把异分母分数转化成同分母分数。
0.12
0.3
×
0.036
12
3
×
36
扩大100倍
扩大10倍
缩小到它的 倍
计算小数乘法时,把小数乘法转化成整数乘法。
转化
未知 →
→ 已知
将什么转化成什么?
转化
复杂 →
→ 简单
推导圆面积公式时, 把圆转化成长方形。
将什么转化成什么?
1.明明和冬冬在同样大小的长方形纸上分别画了一个图案(图中直条的宽度都相等)。 这两个图案的面积相等吗? 为什么?
相等
课堂练习
2.用分数表示下面图形的阴影部分。
8
1
2
1
4
1
4
1
2
1
2
1
3. 你能求出下面各图中涂色部分的周长吗
6×4+3.14×6=42.84(cm)
15×2+3.14×25÷2+25=94.25(cm)
4.如图是程辛在美术课上设计的一幅花瓶图案,这幅图案的周
长和面积分别是多少?(小方格的边长是1厘米)
周长:4×2+3.14×2×2=20.56(厘米)
面积:4×4=16(平方厘米)
答:这幅图案的周长是20.56厘米,面积是16平方厘
米。
5.如图,在一块长方形地中有一条宽为2米的水泥路,则这
条水泥路的面积是多少平方米?
2×10=20(平方米)
答:这条水泥路的面积是20平方米。
6. 求下面各图中涂色部分的面积。(单位:厘米)
第一幅图:8×8=64(平方厘米)
第二幅图:10÷2÷2=2.5(厘米)
3.14×2.52×2=39.25(平方厘米)
提升练习
7. 如图,OA、OB分别为小半圆的直径,且OA=OB=6厘米,∠BOA=90°。涂色部分的面积为多少平方厘米
6×6÷2=18(平方厘米)
[提示]如图,连接AB、OC,将①移到③处,将②移到④处,涂色部分面积即为三角形AOB的面积。
8. 把一个长10厘米、宽4厘米的长方形按如图的方法折叠,涂色部分两个三角形的周长之和是多少厘米
10×2+4×2=28(厘米)
1. 如图正方形中两个涂色长方形的周长和是60厘米,求正方形的面积。
60÷4=15(厘米)
15×15=225(平方厘米)
[提示]两个长方形的周长和等于正方形的周长。先求出正方形的边长,再求面积。
思维拓展
2.如图所示,两个圆的半径都是2厘米,且图中粉色和蓝色
部分的面积相等。EF的长度是多少厘米?
3.14×22÷2=6.28(平方厘米)
6.28÷2=3.14(厘米)
2×2-3.14=0.86(厘米)
答:EF的长度是0.86厘米。
在计算不规则图形的面积和周长时,通常要对不规则图形进行平移或旋转,使之变成已知的或较简单的图形后再进行计算。
课堂小结
这节课你有什么收获?
