7.3 万有引力理论的成就 课件 2023-2024学年高一物理人教版(2019)必修第二册(共21张PPT)
文档属性
| 名称 | 7.3 万有引力理论的成就 课件 2023-2024学年高一物理人教版(2019)必修第二册(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-01-10 16:15:35 | ||
图片预览







文档简介
(共21张PPT)
第3节 万有引力理论的成就
第七章 万有引力与宇宙航行
阿基米德曾说过:“给我一个支点,我就能撬起整个地球。”
那么如果给你一个足够长的杠杆或足够大的天平你是否就可以称量地球的质量了呢?
不可以。
对于地球,我们怎样“称量”它的质量呢?
1.了解万有引力定律在天文学上的应用.
2.会用万有引力定律计算天体的质量和密度.
3.掌握综合运用万有引力定律和圆周运动学知识分析具体问题的方法.
知识点一:“称量”地球的质量
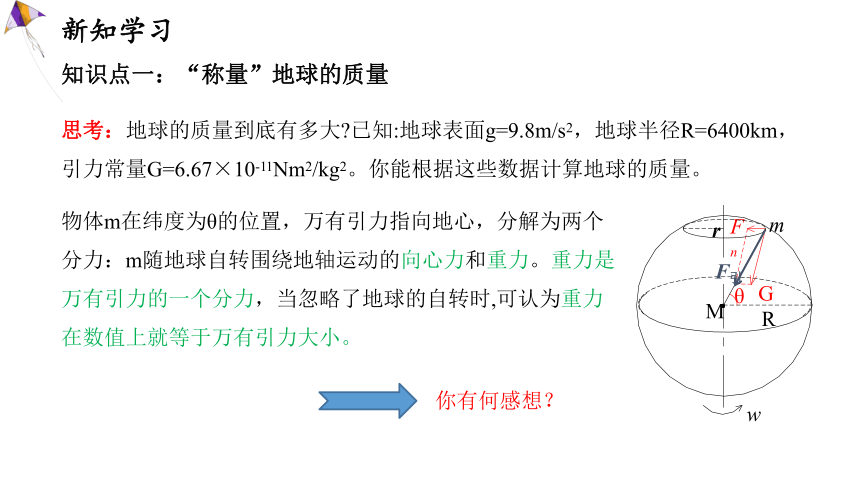
思考:地球的质量到底有多大 已知:地球表面g=9.8m/s2,地球半径R=6400km,引力常量G=6.67×10-11Nm2/kg2。你能根据这些数据计算地球的质量。
θ
Fn
R
M
G
m
w
r
F引
物体m在纬度为θ的位置,万有引力指向地心,分解为两个分力:m随地球自转围绕地轴运动的向心力和重力。重力是万有引力的一个分力,当忽略了地球的自转时,可认为重力在数值上就等于万有引力大小。
你有何感想?
1.理论分析
若不考虑地球自转的影响,地面上物体的重力等于地球对它的引力。
M=
代入数据:
2.数据验证
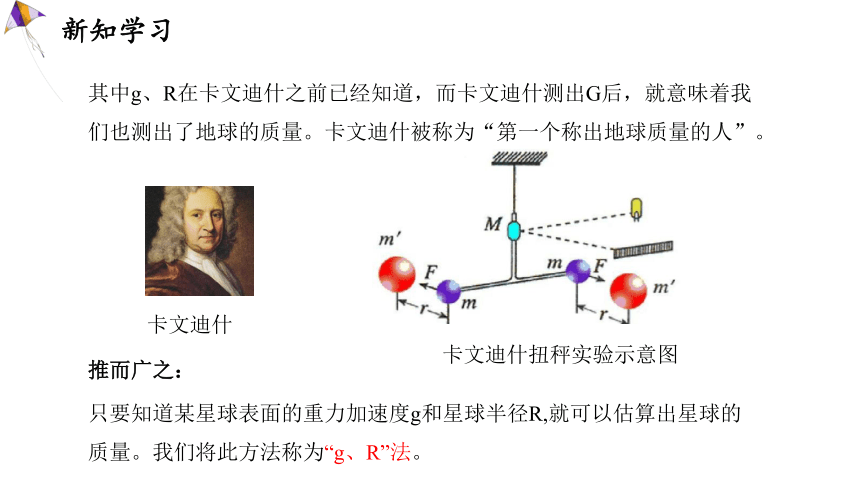
其中g、R在卡文迪什之前已经知道,而卡文迪什测出G后,就意味着我们也测出了地球的质量。卡文迪什被称为“第一个称出地球质量的人”。
卡文迪什
推而广之:
只要知道某星球表面的重力加速度g和星球半径R,就可以估算出星球的质量。我们将此方法称为“g、R”法。
卡文迪什扭秤实验示意图
应用万有引力可算出地球的质量,能否算出太阳的质量呢
(2)万有引力充当向心力 F引=Fn
(1)简化模型:将行星绕太阳的运动看成是匀速圆周运动.
r
M
m
F
r
m太
m
F
(3)依据万有引力定律和牛顿第二定律列出方程,从中解出太阳的质量。
知识点二:计算天体的质量
1、基本思路
设 m太是太阳的质量,m 是某个行星的质量,r 是行星与太阳之间的距离。
解:万有引力充当向心力:
行星运动的角速度 ω 不能直接测出,但可测出它的周期 T。把 ω 和 T 的关系
代入上式得到:
得:
测出行星的公转周期 T 和它与太阳的距离 r,就可以算出太阳的质量,与环行天体质量m无关。
只能求出中心天体的质量。
1.已知太阳与地球间的平均距离约为 1.5×1011m,你能估算太阳的质量吗?换用其他行星的相关数据进行估算,结果会相近吗?为什么?
思考讨论
解:
换用其他行星的相关数据进行估算,结果会相近
虽然不同行星与太阳间的距离 r 和绕太阳公转的周期 T各不相同,但是根据开普勒第三定律,所有行星的 均相同,所以无论选择哪颗行星的轨道半径和公转周期进行计算,所得的太阳质量均相同。
2.怎样计算木星的质量和月球的质量?
要计算木星的质量,对木星的卫星进行测量,只要测得一颗卫星的轨道半径和周期,就可计算木星的质量。
木星和它的卫星
要计算月球的质量,由于人类发射的航天器会环绕月球运行,只要测得航天器绕月运行的轨道半径和周期,就可计算月球的质量。
思考讨论
知识点三:计算天体的密度
问题:如何计算天体密度?
基本思路:
g、R法
T、r法
同理:可用v-r、ω-r、v-T等求质量的方法求天体的密度。
r=R
球体体积V=R3
【例题】已知地球的一颗近地卫星做匀速圆周运动的周期为 T1,已知引力常数为 G,则该天体的密度为多少?若这颗卫星距轨道半径r,测得在该处做匀速圆周运动的周期为 T2,则地球的密度怎样表示呢?
解(1)
则:
地球的体积:
(2)由 得:
知识点四:发现未知天体
海王星
到了 18 世纪,人们已经知道太阳系有 7 颗行星,其中1781 年发现的第七颗行星 —— 天王星的运动轨道有些“古怪”:根据万有引力定律计算出来的轨道与实际观测的结果总有一些偏差。
1、是天文观测数据不准确?
2、是万有引力定律的准确性有问题?
3、是天王星轨道外面还有一颗未发现的行星?
当时有人预测,肯定在其轨道外还有一颗未发现的新星, 英国剑桥大学的学生亚当斯和法国年轻的天文爱好者勒维耶根据天王星的观测资料各自独立地利用万有引力定律计算出来的.这就是后来发现的第八大行星—海王星.
1、海王星的发现
2、海王星的发现的意义
海王星的发现过程充分显示了理论对于实践的巨大指导作用,所用的“计算、预测和观察”的方法指导人们寻找新的天体。
近100 年来,人们在这里发现了冥王星、阋神星等几个较大的天体。
冥王星
阋神星
冥王星为什么被降级为矮行星
冥王星所处的轨道在海王星之外,属于太阳系外围的柯伊伯带,这个区域一直是太阳系小行星和彗星诞生的地方。20世纪90年代以来,天文学家发现柯伊伯带有更多围绕太阳运行的大天体。比如,美国天文学家布朗发现的“2003UB313”,就是一个直径和质量都超过冥王星的天体。
“行星”指的是围绕太阳运转、自身引力足以克服其刚体力而使天体呈圆球状、能够清除其轨道附近其他物体的天体。在太阳系传统的“九大行星”中,只有水星、金星、地球、火星、木星、土星、天王星和海王星符合这些要求。冥王星由于其轨道与海王星的轨道相交,不符合新的行星定义,因此被自动降级为“矮行星”。
知识点五:预言哈雷彗星回归
哈雷依据万有引力定律,用一年时间计算了它们的轨道。发现 1531 年、1607 年和 1682 年出现的这三颗彗星轨道看起来如出一辙,他大胆预言,这三次出现的彗星是同一颗星(图 7.3-3),周期约为 76 年,并预言它将于 1758 年底或 1759 年初再次回归。1759 年 3 月这颗彗星如期通过了近日点,它最近一次回归是 1986 年,它的下次回归将在2061 年左右。
1.随着太空技术的飞速发展,人类登陆其它星球成为可能。假设未来的某一天,宇航员登上某一星球后,测得该星球质量是地球质量的8倍,而该星球的平均密度与地球的相等,则该星球表面的重力加速度是地球表面重力加速度的( )
A.0.5倍 B.2倍 C.4倍 D.8倍
B
2、(多选题)航天飞机在围绕地球做匀速圆周运动过程中,下列关于宇航员的说法中正确( )
A.宇航员不再受重力作用
B.宇航员受的重力提供其做匀速圆周运动的向心力
C.宇航员处于完全失重状态
D.宇航员对座椅的压力为零
BCD
3、 (多选)2020年7月23日12时41分,长征五号运载火箭在中国文昌航天发射场点火起飞,成功将天问一号火星探测器送入预定轨道。假设天问一号在着陆之前绕火星表面做近地圆周运动的半径为r1、周期为T1;火星绕太阳做圆周运动的半径为r2、周期为T2,引力常量为G。根据以上条件能得出( )
A.火星的密度
B.太阳对火星的引力大小
C.天问一号的质量
D.关系式
AB
一、“称量”地球的质量
二、计算天体的质量
得:
只能求出中心天体的质量。
三、计算天体的密度
得:
四、发现未知天体
五、预言哈雷彗星回归
第3节 万有引力理论的成就
第七章 万有引力与宇宙航行
阿基米德曾说过:“给我一个支点,我就能撬起整个地球。”
那么如果给你一个足够长的杠杆或足够大的天平你是否就可以称量地球的质量了呢?
不可以。
对于地球,我们怎样“称量”它的质量呢?
1.了解万有引力定律在天文学上的应用.
2.会用万有引力定律计算天体的质量和密度.
3.掌握综合运用万有引力定律和圆周运动学知识分析具体问题的方法.
知识点一:“称量”地球的质量
思考:地球的质量到底有多大 已知:地球表面g=9.8m/s2,地球半径R=6400km,引力常量G=6.67×10-11Nm2/kg2。你能根据这些数据计算地球的质量。
θ
Fn
R
M
G
m
w
r
F引
物体m在纬度为θ的位置,万有引力指向地心,分解为两个分力:m随地球自转围绕地轴运动的向心力和重力。重力是万有引力的一个分力,当忽略了地球的自转时,可认为重力在数值上就等于万有引力大小。
你有何感想?
1.理论分析
若不考虑地球自转的影响,地面上物体的重力等于地球对它的引力。
M=
代入数据:
2.数据验证
其中g、R在卡文迪什之前已经知道,而卡文迪什测出G后,就意味着我们也测出了地球的质量。卡文迪什被称为“第一个称出地球质量的人”。
卡文迪什
推而广之:
只要知道某星球表面的重力加速度g和星球半径R,就可以估算出星球的质量。我们将此方法称为“g、R”法。
卡文迪什扭秤实验示意图
应用万有引力可算出地球的质量,能否算出太阳的质量呢
(2)万有引力充当向心力 F引=Fn
(1)简化模型:将行星绕太阳的运动看成是匀速圆周运动.
r
M
m
F
r
m太
m
F
(3)依据万有引力定律和牛顿第二定律列出方程,从中解出太阳的质量。
知识点二:计算天体的质量
1、基本思路
设 m太是太阳的质量,m 是某个行星的质量,r 是行星与太阳之间的距离。
解:万有引力充当向心力:
行星运动的角速度 ω 不能直接测出,但可测出它的周期 T。把 ω 和 T 的关系
代入上式得到:
得:
测出行星的公转周期 T 和它与太阳的距离 r,就可以算出太阳的质量,与环行天体质量m无关。
只能求出中心天体的质量。
1.已知太阳与地球间的平均距离约为 1.5×1011m,你能估算太阳的质量吗?换用其他行星的相关数据进行估算,结果会相近吗?为什么?
思考讨论
解:
换用其他行星的相关数据进行估算,结果会相近
虽然不同行星与太阳间的距离 r 和绕太阳公转的周期 T各不相同,但是根据开普勒第三定律,所有行星的 均相同,所以无论选择哪颗行星的轨道半径和公转周期进行计算,所得的太阳质量均相同。
2.怎样计算木星的质量和月球的质量?
要计算木星的质量,对木星的卫星进行测量,只要测得一颗卫星的轨道半径和周期,就可计算木星的质量。
木星和它的卫星
要计算月球的质量,由于人类发射的航天器会环绕月球运行,只要测得航天器绕月运行的轨道半径和周期,就可计算月球的质量。
思考讨论
知识点三:计算天体的密度
问题:如何计算天体密度?
基本思路:
g、R法
T、r法
同理:可用v-r、ω-r、v-T等求质量的方法求天体的密度。
r=R
球体体积V=R3
【例题】已知地球的一颗近地卫星做匀速圆周运动的周期为 T1,已知引力常数为 G,则该天体的密度为多少?若这颗卫星距轨道半径r,测得在该处做匀速圆周运动的周期为 T2,则地球的密度怎样表示呢?
解(1)
则:
地球的体积:
(2)由 得:
知识点四:发现未知天体
海王星
到了 18 世纪,人们已经知道太阳系有 7 颗行星,其中1781 年发现的第七颗行星 —— 天王星的运动轨道有些“古怪”:根据万有引力定律计算出来的轨道与实际观测的结果总有一些偏差。
1、是天文观测数据不准确?
2、是万有引力定律的准确性有问题?
3、是天王星轨道外面还有一颗未发现的行星?
当时有人预测,肯定在其轨道外还有一颗未发现的新星, 英国剑桥大学的学生亚当斯和法国年轻的天文爱好者勒维耶根据天王星的观测资料各自独立地利用万有引力定律计算出来的.这就是后来发现的第八大行星—海王星.
1、海王星的发现
2、海王星的发现的意义
海王星的发现过程充分显示了理论对于实践的巨大指导作用,所用的“计算、预测和观察”的方法指导人们寻找新的天体。
近100 年来,人们在这里发现了冥王星、阋神星等几个较大的天体。
冥王星
阋神星
冥王星为什么被降级为矮行星
冥王星所处的轨道在海王星之外,属于太阳系外围的柯伊伯带,这个区域一直是太阳系小行星和彗星诞生的地方。20世纪90年代以来,天文学家发现柯伊伯带有更多围绕太阳运行的大天体。比如,美国天文学家布朗发现的“2003UB313”,就是一个直径和质量都超过冥王星的天体。
“行星”指的是围绕太阳运转、自身引力足以克服其刚体力而使天体呈圆球状、能够清除其轨道附近其他物体的天体。在太阳系传统的“九大行星”中,只有水星、金星、地球、火星、木星、土星、天王星和海王星符合这些要求。冥王星由于其轨道与海王星的轨道相交,不符合新的行星定义,因此被自动降级为“矮行星”。
知识点五:预言哈雷彗星回归
哈雷依据万有引力定律,用一年时间计算了它们的轨道。发现 1531 年、1607 年和 1682 年出现的这三颗彗星轨道看起来如出一辙,他大胆预言,这三次出现的彗星是同一颗星(图 7.3-3),周期约为 76 年,并预言它将于 1758 年底或 1759 年初再次回归。1759 年 3 月这颗彗星如期通过了近日点,它最近一次回归是 1986 年,它的下次回归将在2061 年左右。
1.随着太空技术的飞速发展,人类登陆其它星球成为可能。假设未来的某一天,宇航员登上某一星球后,测得该星球质量是地球质量的8倍,而该星球的平均密度与地球的相等,则该星球表面的重力加速度是地球表面重力加速度的( )
A.0.5倍 B.2倍 C.4倍 D.8倍
B
2、(多选题)航天飞机在围绕地球做匀速圆周运动过程中,下列关于宇航员的说法中正确( )
A.宇航员不再受重力作用
B.宇航员受的重力提供其做匀速圆周运动的向心力
C.宇航员处于完全失重状态
D.宇航员对座椅的压力为零
BCD
3、 (多选)2020年7月23日12时41分,长征五号运载火箭在中国文昌航天发射场点火起飞,成功将天问一号火星探测器送入预定轨道。假设天问一号在着陆之前绕火星表面做近地圆周运动的半径为r1、周期为T1;火星绕太阳做圆周运动的半径为r2、周期为T2,引力常量为G。根据以上条件能得出( )
A.火星的密度
B.太阳对火星的引力大小
C.天问一号的质量
D.关系式
AB
一、“称量”地球的质量
二、计算天体的质量
得:
只能求出中心天体的质量。
三、计算天体的密度
得:
四、发现未知天体
五、预言哈雷彗星回归
