8.1 功与功率 第2课时 课件 2023-2024学年高一物理人教版(2019)必修第二册(共25张PPT)
文档属性
| 名称 | 8.1 功与功率 第2课时 课件 2023-2024学年高一物理人教版(2019)必修第二册(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-01-10 16:19:55 | ||
图片预览







文档简介
(共25张PPT)
宣讲人:某某某 时间:20XX.XX
第1节 功和功率 第2课时
第八章 机械能守恒定律
学习目标
1.学会用多角度求变力做功,增强对功的知识的理解。
2.学会用控制变量法分析汽车的两种启动方式,加强对公式的理解与应用。
目录
02
01
变力做功
机车的两种启动方式
功的计算公式W=Flcos α只适用于恒力做功的情况,对于变力做功的计算是学习的难点,也是重点。我们有哪些方法可以解决变力做功的问题呢?或者说我们能不能把变力转化成恒力来处理呢?
问题
知识点一:变力做功
1.等效转化法
方法指导:变力做功直接求解时,比较复杂,但若通过转换研究的对象,有时可化为恒力做功,可以用W=Flcosα求解。
【典例1】如图,用恒力F通过跨过光滑定滑轮的轻绳,将静止于水平面上的物体从位置A拉到位置B,物体和滑轮的大小均忽略,定滑轮距水平面高为h,物体在位置A、B时,细绳与水平面的夹角分别为α和β,求绳的拉力F对物体做的功。
【分析】功是能量转化的量度,轻绳不存储能量,恒力F做功通过绳子将能量转移到物体上,故此恒力F做功应该等于绳子对物体做的功。
h
2.平均值法
(2)平均值法:如果物体受到的力是随着位移均匀变化的,则可以利用用公式 求变力做功,物体受到的平均力的大小 ,其中F1为物体初状态时受到的力,F2为物体末状态时受到的力。
(1)分段法:力在全程是变力,但在每一个阶段是恒力,这样就可以先计算每个阶段做的功,再利用求和的方法计算整个过程中变力做的功。
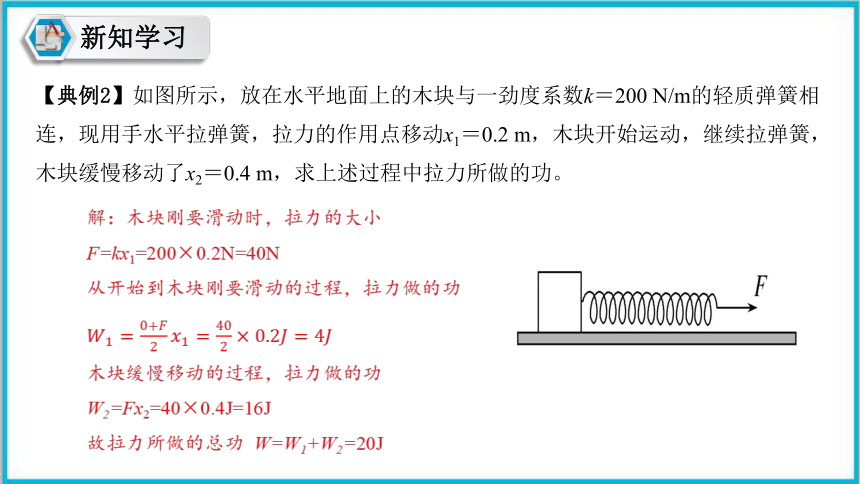
【典例2】如图所示,放在水平地面上的木块与一劲度系数k=200 N/m的轻质弹簧相连,现用手水平拉弹簧,拉力的作用点移动x1=0.2 m,木块开始运动,继续拉弹簧,木块缓慢移动了x2=0.4 m,求上述过程中拉力所做的功。
解:木块刚要滑动时,拉力的大小
F=kx1=200×0.2N=40N
从开始到木块刚要滑动的过程,拉力做的功
木块缓慢移动的过程,拉力做的功
W2=Fx2=40×0.4J=16J
故拉力所做的总功 W=W1+W2=20J
3.图像法
在F -x图象中,图线与x轴所围的“面积”的代数和表示F做功。“面积”有正负,在x轴上方的“面积”为正,在x轴下方的“面积”为负。如图甲、乙所示,这与运动学中由v-t图象求位移的原理相同。
【例题3】一个物体所受的力F随位移l变化的图像如图所示,在这一过程中,力F对物体做的功为( )
A.3 J B.6 J C.7 J D.8 J
【解析】力F对物体做的功等于l轴上方梯形“面积”所表示的正功与l轴下方三角形“面积”所表示的负功的代数和。W1=×(3+4)×2 J=7 J,W2=- ×(5-4)×2 J=-1 J,所以力F对物体做的功为W=7 J-1 J=6 J,选项B正确。
4.微元法
当力的大小不变,力的方向时刻与速度同向(或反向)时,把物体的运动过程分为很多小段,这样每一小段可以看成直线,先求力在每一小段上做的功,再求和即可。
例如,滑动摩擦力、空气阻力总与物体相对运动的方向相反,可把运动过程细分,其中每一小段都是恒力做功,整个运动过程中所做的总功是各个阶段所做功的和,即力与路程的乘积。
【典例4】如图所示,质量为m的质点在力F的作用下,沿水平面上半径为R的光滑圆槽运动一周。若F的大小不变,方向始终与圆槽相切(与速度的方向相同),求力F对质点做的功。
【解析】质点在运动的过程中,F的方向始终与速度的方向相同,若将圆周分成许多极短的小圆弧Δl1、Δl2、Δl3、…、Δln,则每段小圆弧都可以看成一段极短的直线,所以质点运动一周,力F对质点做的功等于它在每一小段上做功的代数和,即W=W1+W2+…+Wn=F(Δl1+Δl2+…+Δln)=2πRF。
知识点二:机车的两种启动方式
机车在行驶的过程中,发动机的最大功率等于额定功率。
P=F v
v
瞬时速度
功率
牵引力
1.以恒定功率P额启动;
机车的启动方式有两种:
2.在恒定的牵引力F作用下匀加速启动。
v
t
0
当F=F阻时,a=0 ,v达到最大
保持 vm
匀速
v
F=
v
P
a=
m
F-F阻
↑
→
↓
↑
→
→
↓
↓
F阻
F牵
F阻
F牵
vm
v—t 图象
加速阶段
的图象
匀速阶段
的图象
a减小的变加速运动
匀速运动
v0=0,P恒=P额
vm
1.以恒定功率P额启动
1.F为变力时,发动机做的功只能用
W=Pt 计算,不能用W =Fl 计算。
2.达到最大速度的本质条件是:a=0
vm
v
t
0
说明:
3.达到最大速度时,有 P额=F阻vm
当F= F阻时,
a=0 ,v达到最大
保持
vm
匀速
F=
v
P额
a=
m
F-F阻
↑
→
↓
v
↑
↓
→
→
↓
vm=
F阻
P额
加速度逐渐减小的变加速直线运动
匀速直线运动
a=
m
F-F阻
→
→
→
→
F
→
v
↑
P =F v
↑
↑
→
当P= P额时,保持P额继续加速
匀加速直线运动
2.以恒定加速度启动
v0=0,F恒
F阻
F牵
F牵=F阻,vm=P/F阻
F阻
F牵
vm
v↑,P=P额
v—t
图象
匀加速阶段的图象
匀速阶段的图象
匀加速运动
匀速运动
a减小的变加速直线运动
变加速阶段的图象
v
t
0
vm
机车做匀加速运动只能维持一段时间,当功率增大到额定功率时,匀加速运动结束,匀加速时间为:
t1=
P额
(ma+f阻)a
t1
v1
v
t
0
vm
说明:
2.匀加速结束的条件是:P实=Pmax=P额
3.当匀加速结束时速度为v1,P额=Fv1=f阻Vm (其中F=ma+f阻)
1.达到最大速度的本质条件:a=0
【典例1】拖拉机耕地时一般比在道路上行驶时速度慢,这样做的主要目的是( )
A.节省燃料 B.提高柴油机的功率
C.提高传动机械的效率 D.增大拖拉机的牵引力
D
【典例2】(多选)按额定功率行驶的汽车,所受地面的阻力保持不变,则 ( )
A.汽车加速行驶时,牵引力不变,速度增大
B.汽车可以做匀加速运动
C.汽车加速行驶时,加速度逐渐减小,速度逐渐增大
D.汽车达到最大速度时,所受合力为零
CD
1.用铁锤把小铁钉钉入木板,设木板对铁钉的阻力与铁钉进入木板的深度成正比。已知铁锤第一次使铁钉进入木板的深度为d,接着敲第二锤,如果铁锤第二次敲铁钉时对铁钉做的功与第一次相同,那么,第二次使铁钉进入木板的深度为( )
2.用质量为5 kg的均匀铁索,从10 m深的井中吊起一质量为20 kg的物体,此过程中人的拉力随物体上升的高度变化如图所示,在这个过程中人至少要做多少功?(g取10 m/s2)
3.在水平面上,有一弯曲的槽道AB,槽道由半径分别为和R的两个半圆构成。如图所示,现用大小恒为F的拉力将一光滑小球从A点沿槽道拉至B点,若拉力F的方向时刻均与小球运动方向一致,则此过程中拉力所做的功为( )
A.0 B.FR C. D.2πFR
4.(多选)火车从车站开出做匀加速运动,若阻力与速度成正比,则( )
A.火车发动机的功率一定越来越大,牵引力越来越大
B.火车发动机的功率恒定不变,牵引力越来越小
C.当火车达到某一速率时,若要保持此速率做匀速运动,则发动机的功率这时应减小
D.当火车达到某一速率时,若要保持此速率做匀速运动,则发动机的功率一定跟此时速率的二次方成正比
ACD
宣讲人:某某某 时间:20XX.XX
第1节 功和功率 第2课时
第八章 机械能守恒定律
学习目标
1.学会用多角度求变力做功,增强对功的知识的理解。
2.学会用控制变量法分析汽车的两种启动方式,加强对公式的理解与应用。
目录
02
01
变力做功
机车的两种启动方式
功的计算公式W=Flcos α只适用于恒力做功的情况,对于变力做功的计算是学习的难点,也是重点。我们有哪些方法可以解决变力做功的问题呢?或者说我们能不能把变力转化成恒力来处理呢?
问题
知识点一:变力做功
1.等效转化法
方法指导:变力做功直接求解时,比较复杂,但若通过转换研究的对象,有时可化为恒力做功,可以用W=Flcosα求解。
【典例1】如图,用恒力F通过跨过光滑定滑轮的轻绳,将静止于水平面上的物体从位置A拉到位置B,物体和滑轮的大小均忽略,定滑轮距水平面高为h,物体在位置A、B时,细绳与水平面的夹角分别为α和β,求绳的拉力F对物体做的功。
【分析】功是能量转化的量度,轻绳不存储能量,恒力F做功通过绳子将能量转移到物体上,故此恒力F做功应该等于绳子对物体做的功。
h
2.平均值法
(2)平均值法:如果物体受到的力是随着位移均匀变化的,则可以利用用公式 求变力做功,物体受到的平均力的大小 ,其中F1为物体初状态时受到的力,F2为物体末状态时受到的力。
(1)分段法:力在全程是变力,但在每一个阶段是恒力,这样就可以先计算每个阶段做的功,再利用求和的方法计算整个过程中变力做的功。
【典例2】如图所示,放在水平地面上的木块与一劲度系数k=200 N/m的轻质弹簧相连,现用手水平拉弹簧,拉力的作用点移动x1=0.2 m,木块开始运动,继续拉弹簧,木块缓慢移动了x2=0.4 m,求上述过程中拉力所做的功。
解:木块刚要滑动时,拉力的大小
F=kx1=200×0.2N=40N
从开始到木块刚要滑动的过程,拉力做的功
木块缓慢移动的过程,拉力做的功
W2=Fx2=40×0.4J=16J
故拉力所做的总功 W=W1+W2=20J
3.图像法
在F -x图象中,图线与x轴所围的“面积”的代数和表示F做功。“面积”有正负,在x轴上方的“面积”为正,在x轴下方的“面积”为负。如图甲、乙所示,这与运动学中由v-t图象求位移的原理相同。
【例题3】一个物体所受的力F随位移l变化的图像如图所示,在这一过程中,力F对物体做的功为( )
A.3 J B.6 J C.7 J D.8 J
【解析】力F对物体做的功等于l轴上方梯形“面积”所表示的正功与l轴下方三角形“面积”所表示的负功的代数和。W1=×(3+4)×2 J=7 J,W2=- ×(5-4)×2 J=-1 J,所以力F对物体做的功为W=7 J-1 J=6 J,选项B正确。
4.微元法
当力的大小不变,力的方向时刻与速度同向(或反向)时,把物体的运动过程分为很多小段,这样每一小段可以看成直线,先求力在每一小段上做的功,再求和即可。
例如,滑动摩擦力、空气阻力总与物体相对运动的方向相反,可把运动过程细分,其中每一小段都是恒力做功,整个运动过程中所做的总功是各个阶段所做功的和,即力与路程的乘积。
【典例4】如图所示,质量为m的质点在力F的作用下,沿水平面上半径为R的光滑圆槽运动一周。若F的大小不变,方向始终与圆槽相切(与速度的方向相同),求力F对质点做的功。
【解析】质点在运动的过程中,F的方向始终与速度的方向相同,若将圆周分成许多极短的小圆弧Δl1、Δl2、Δl3、…、Δln,则每段小圆弧都可以看成一段极短的直线,所以质点运动一周,力F对质点做的功等于它在每一小段上做功的代数和,即W=W1+W2+…+Wn=F(Δl1+Δl2+…+Δln)=2πRF。
知识点二:机车的两种启动方式
机车在行驶的过程中,发动机的最大功率等于额定功率。
P=F v
v
瞬时速度
功率
牵引力
1.以恒定功率P额启动;
机车的启动方式有两种:
2.在恒定的牵引力F作用下匀加速启动。
v
t
0
当F=F阻时,a=0 ,v达到最大
保持 vm
匀速
v
F=
v
P
a=
m
F-F阻
↑
→
↓
↑
→
→
↓
↓
F阻
F牵
F阻
F牵
vm
v—t 图象
加速阶段
的图象
匀速阶段
的图象
a减小的变加速运动
匀速运动
v0=0,P恒=P额
vm
1.以恒定功率P额启动
1.F为变力时,发动机做的功只能用
W=Pt 计算,不能用W =Fl 计算。
2.达到最大速度的本质条件是:a=0
vm
v
t
0
说明:
3.达到最大速度时,有 P额=F阻vm
当F= F阻时,
a=0 ,v达到最大
保持
vm
匀速
F=
v
P额
a=
m
F-F阻
↑
→
↓
v
↑
↓
→
→
↓
vm=
F阻
P额
加速度逐渐减小的变加速直线运动
匀速直线运动
a=
m
F-F阻
→
→
→
→
F
→
v
↑
P =F v
↑
↑
→
当P= P额时,保持P额继续加速
匀加速直线运动
2.以恒定加速度启动
v0=0,F恒
F阻
F牵
F牵=F阻,vm=P/F阻
F阻
F牵
vm
v↑,P=P额
v—t
图象
匀加速阶段的图象
匀速阶段的图象
匀加速运动
匀速运动
a减小的变加速直线运动
变加速阶段的图象
v
t
0
vm
机车做匀加速运动只能维持一段时间,当功率增大到额定功率时,匀加速运动结束,匀加速时间为:
t1=
P额
(ma+f阻)a
t1
v1
v
t
0
vm
说明:
2.匀加速结束的条件是:P实=Pmax=P额
3.当匀加速结束时速度为v1,P额=Fv1=f阻Vm (其中F=ma+f阻)
1.达到最大速度的本质条件:a=0
【典例1】拖拉机耕地时一般比在道路上行驶时速度慢,这样做的主要目的是( )
A.节省燃料 B.提高柴油机的功率
C.提高传动机械的效率 D.增大拖拉机的牵引力
D
【典例2】(多选)按额定功率行驶的汽车,所受地面的阻力保持不变,则 ( )
A.汽车加速行驶时,牵引力不变,速度增大
B.汽车可以做匀加速运动
C.汽车加速行驶时,加速度逐渐减小,速度逐渐增大
D.汽车达到最大速度时,所受合力为零
CD
1.用铁锤把小铁钉钉入木板,设木板对铁钉的阻力与铁钉进入木板的深度成正比。已知铁锤第一次使铁钉进入木板的深度为d,接着敲第二锤,如果铁锤第二次敲铁钉时对铁钉做的功与第一次相同,那么,第二次使铁钉进入木板的深度为( )
2.用质量为5 kg的均匀铁索,从10 m深的井中吊起一质量为20 kg的物体,此过程中人的拉力随物体上升的高度变化如图所示,在这个过程中人至少要做多少功?(g取10 m/s2)
3.在水平面上,有一弯曲的槽道AB,槽道由半径分别为和R的两个半圆构成。如图所示,现用大小恒为F的拉力将一光滑小球从A点沿槽道拉至B点,若拉力F的方向时刻均与小球运动方向一致,则此过程中拉力所做的功为( )
A.0 B.FR C. D.2πFR
4.(多选)火车从车站开出做匀加速运动,若阻力与速度成正比,则( )
A.火车发动机的功率一定越来越大,牵引力越来越大
B.火车发动机的功率恒定不变,牵引力越来越小
C.当火车达到某一速率时,若要保持此速率做匀速运动,则发动机的功率这时应减小
D.当火车达到某一速率时,若要保持此速率做匀速运动,则发动机的功率一定跟此时速率的二次方成正比
ACD
