8.2 重力势能 第2课时 课件 2023-2024学年高一物理人教版(2019)必修第二册(共18张PPT)
文档属性
| 名称 | 8.2 重力势能 第2课时 课件 2023-2024学年高一物理人教版(2019)必修第二册(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-01-10 16:21:00 | ||
图片预览





文档简介
(共18张PPT)
宣讲人:某某某 时间:20XX.XX
第2节 重力势能 第2课时
第八章 机械能守恒定律
学习目标
1.知道探究弹性势能表达式的方法。
2.理解弹性势能的概念,会分析决定弹性势能大小的相关因素。
3.体会探究过程的猜想、分析和转化的方法。
4.领悟求弹力做功时,通过细分过程化变力为恒力的思想方法。
目录
01
弹性势能
02
探究影响弹性势能大小的因素
03
求弹力做功
04
弹簧的弹性势能与弹力做功的关系
05
弹性势能的表达式
在人的作用下几张图片中的物体都有什么共同点?
知识点一:弹性势能
发生弹性形变的物体的各部分之间,由于有弹力的相互作用,也具有势能,这种势能叫做弹性势能。
物体具有弹性势能的条件是发生弹性形变。
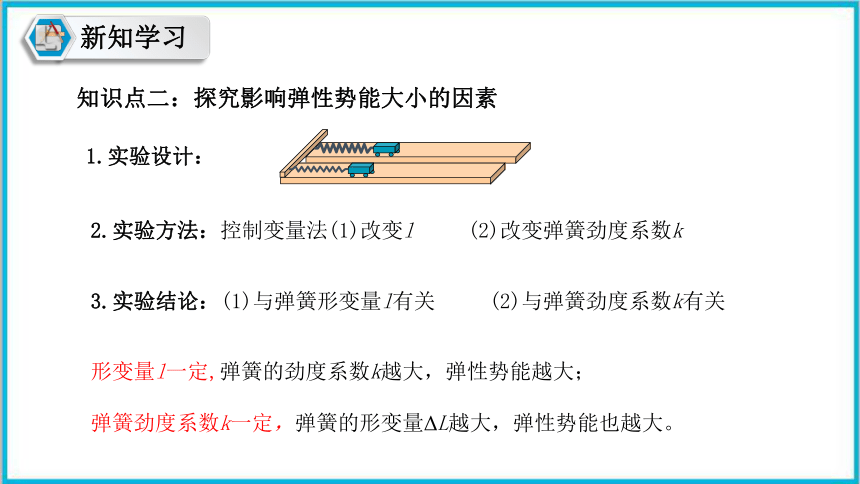
知识点二:探究影响弹性势能大小的因素
1.实验设计:
2.实验方法:控制变量法(1)改变l (2)改变弹簧劲度系数k
3.实验结论:(1)与弹簧形变量l有关 (2)与弹簧劲度系数k有关
形变量l一定,弹簧的劲度系数k越大,弹性势能越大;
弹簧劲度系数k一定,弹簧的形变量ΔL越大,弹性势能也越大。
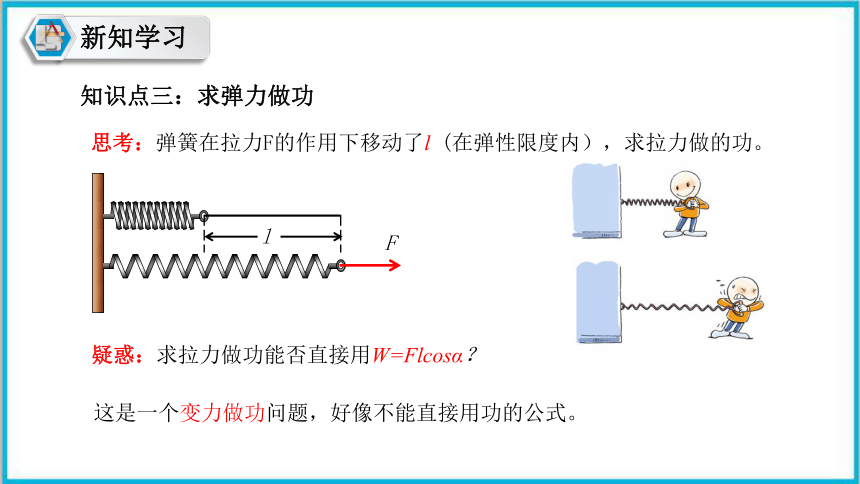
知识点三:求弹力做功
疑惑:求拉力做功能否直接用W=Flcosα?
这是一个变力做功问题,好像不能直接用功的公式。
F
l
思考:弹簧在拉力F的作用下移动了l (在弹性限度内),求拉力做的功。
方法一:平均值法
因拉力F与形变量l成正比,故拉力的平均值为 :
平均拉力对这段位移做的功:
F拉
l
F = k l
方法二:微元法
把弹簧从A到B的过程分成很多小段:Δl1、Δl2、Δl3…
在各个小段上,弹力可近似认为是不变的:F1、F2、F3 …
F拉
在各小段上,拉力做的功分别是:F1Δl1、F2Δl2、F3Δl3 …
拉力在全过程中所做的功为: W拉=F1Δl1+F2Δl2+F3Δl3+…
怎样计算这个求和式?
方法三:微元法+图像法
联想
o
t
v
vo
o
t
v
vo
o
t
v
vo
o
t
v
vo
计算匀加速直线运动位移时曾经用过的方法
怎样计算这个求和式?
W=F1Δl1+F2Δl2+F3Δl3+…
F拉
l
F
0
l
l
Δl1
Δl2
Δl3
Δl5
Δl4
F2
F3
F4
F5
F1
F = k l
拉力所做的功等于图线与横轴所围的面积
W拉= k l 2
1
2
知识点四:弹簧的弹性势能与弹力做功的关系
重力做功
重力势能的变化
重力做正功,重力势能减小;重力做负功,重力势能增加。
弹力做正功,弹性势能减小;
弹力做负功,弹性势能增加。
弹性势能的变化
弹力做功
回顾:
类比可得:
WF弹=EP1-EP2= -△ EP
弹力做的功
初态的弹性势能
末态的弹性势能
关系式:
关系:弹力做功是弹性势能变化的量度。
知识点五:弹性势能的表达式
可见弹簧的弹性势能表达式为:
l为弹簧的形变量
k为弹簧的劲度系数
WF弹=-WF拉=EP1-EP2
l
Δl1
Δl2
Δl3
Δl5
Δl4
F拉
F弹
WF拉=k l 2
EP1=0 ,
弹性势能 重力势能
定义 发生弹性形变的物体各部分之间由于弹力的相互作用而具有的势能 被举高的物体由于相对地球的位置发生变化具有的势能
物理情景 弹簧的伸长和压缩 人从一楼上到四楼
受力特征 弹簧的弹力随形变量的增加而增大,是变力 地球附近的重力加速度恒定,重力是恒力
表达式
相对性 弹性势能的大小与零势能位置的选取有关,通常选弹簧长度为原长时,弹性势能为零 重力势能的大小与零势能面的选取有关,但其变化量与参考平面的选取无关
势能的变化 弹簧弹力做负功,弹簧形变量增加,弹性势能增加 重力做负功,重力势能增加
1、如图,在一次“蹦极”运动中,人由高空跃下到最低点的整个过程中,下列说法正确的是( )
A.重力对人做正功
B.人的重力势能减小了
C.“蹦极”绳对人做负功
D.“蹦极”绳的弹性势能增加了
AB
2、如图所示,在光滑的水平面上有一物体,它的左端连一弹簧,弹簧的另一端固定在墙上,在力F作用下物体处于静止状态。当撤去F后,物体将向右运动,在物体向右运动过程 中下列说法正确的是 ( )
A、弹簧的弹性势能逐渐减小
B、弹簧的弹性势能逐渐增大
C、弹簧的弹性势能先增大再减小
D、弹簧的弹性势能先减小再增大
B
F
D
3.如图所示,轻质弹簧下悬挂一个小球,手掌托小球使之缓慢上移,弹簧恢复原长时迅速撤去手掌使小球开始下落。不计空气阻力,取弹簧处于原长时的弹性势能为零。撤去手掌后,下列说法正确的是( )
A.刚撤去手掌瞬间,弹簧弹力等于小球重力
B.小球速度最大时,弹簧的弹性势能为零
c.弹簧的弹性势能最大时,小球速度为零
D.小球运动到最高点时,弹簧的弹性势能最大
C
宣讲人:某某某 时间:20XX.XX
第2节 重力势能 第2课时
第八章 机械能守恒定律
学习目标
1.知道探究弹性势能表达式的方法。
2.理解弹性势能的概念,会分析决定弹性势能大小的相关因素。
3.体会探究过程的猜想、分析和转化的方法。
4.领悟求弹力做功时,通过细分过程化变力为恒力的思想方法。
目录
01
弹性势能
02
探究影响弹性势能大小的因素
03
求弹力做功
04
弹簧的弹性势能与弹力做功的关系
05
弹性势能的表达式
在人的作用下几张图片中的物体都有什么共同点?
知识点一:弹性势能
发生弹性形变的物体的各部分之间,由于有弹力的相互作用,也具有势能,这种势能叫做弹性势能。
物体具有弹性势能的条件是发生弹性形变。
知识点二:探究影响弹性势能大小的因素
1.实验设计:
2.实验方法:控制变量法(1)改变l (2)改变弹簧劲度系数k
3.实验结论:(1)与弹簧形变量l有关 (2)与弹簧劲度系数k有关
形变量l一定,弹簧的劲度系数k越大,弹性势能越大;
弹簧劲度系数k一定,弹簧的形变量ΔL越大,弹性势能也越大。
知识点三:求弹力做功
疑惑:求拉力做功能否直接用W=Flcosα?
这是一个变力做功问题,好像不能直接用功的公式。
F
l
思考:弹簧在拉力F的作用下移动了l (在弹性限度内),求拉力做的功。
方法一:平均值法
因拉力F与形变量l成正比,故拉力的平均值为 :
平均拉力对这段位移做的功:
F拉
l
F = k l
方法二:微元法
把弹簧从A到B的过程分成很多小段:Δl1、Δl2、Δl3…
在各个小段上,弹力可近似认为是不变的:F1、F2、F3 …
F拉
在各小段上,拉力做的功分别是:F1Δl1、F2Δl2、F3Δl3 …
拉力在全过程中所做的功为: W拉=F1Δl1+F2Δl2+F3Δl3+…
怎样计算这个求和式?
方法三:微元法+图像法
联想
o
t
v
vo
o
t
v
vo
o
t
v
vo
o
t
v
vo
计算匀加速直线运动位移时曾经用过的方法
怎样计算这个求和式?
W=F1Δl1+F2Δl2+F3Δl3+…
F拉
l
F
0
l
l
Δl1
Δl2
Δl3
Δl5
Δl4
F2
F3
F4
F5
F1
F = k l
拉力所做的功等于图线与横轴所围的面积
W拉= k l 2
1
2
知识点四:弹簧的弹性势能与弹力做功的关系
重力做功
重力势能的变化
重力做正功,重力势能减小;重力做负功,重力势能增加。
弹力做正功,弹性势能减小;
弹力做负功,弹性势能增加。
弹性势能的变化
弹力做功
回顾:
类比可得:
WF弹=EP1-EP2= -△ EP
弹力做的功
初态的弹性势能
末态的弹性势能
关系式:
关系:弹力做功是弹性势能变化的量度。
知识点五:弹性势能的表达式
可见弹簧的弹性势能表达式为:
l为弹簧的形变量
k为弹簧的劲度系数
WF弹=-WF拉=EP1-EP2
l
Δl1
Δl2
Δl3
Δl5
Δl4
F拉
F弹
WF拉=k l 2
EP1=0 ,
弹性势能 重力势能
定义 发生弹性形变的物体各部分之间由于弹力的相互作用而具有的势能 被举高的物体由于相对地球的位置发生变化具有的势能
物理情景 弹簧的伸长和压缩 人从一楼上到四楼
受力特征 弹簧的弹力随形变量的增加而增大,是变力 地球附近的重力加速度恒定,重力是恒力
表达式
相对性 弹性势能的大小与零势能位置的选取有关,通常选弹簧长度为原长时,弹性势能为零 重力势能的大小与零势能面的选取有关,但其变化量与参考平面的选取无关
势能的变化 弹簧弹力做负功,弹簧形变量增加,弹性势能增加 重力做负功,重力势能增加
1、如图,在一次“蹦极”运动中,人由高空跃下到最低点的整个过程中,下列说法正确的是( )
A.重力对人做正功
B.人的重力势能减小了
C.“蹦极”绳对人做负功
D.“蹦极”绳的弹性势能增加了
AB
2、如图所示,在光滑的水平面上有一物体,它的左端连一弹簧,弹簧的另一端固定在墙上,在力F作用下物体处于静止状态。当撤去F后,物体将向右运动,在物体向右运动过程 中下列说法正确的是 ( )
A、弹簧的弹性势能逐渐减小
B、弹簧的弹性势能逐渐增大
C、弹簧的弹性势能先增大再减小
D、弹簧的弹性势能先减小再增大
B
F
D
3.如图所示,轻质弹簧下悬挂一个小球,手掌托小球使之缓慢上移,弹簧恢复原长时迅速撤去手掌使小球开始下落。不计空气阻力,取弹簧处于原长时的弹性势能为零。撤去手掌后,下列说法正确的是( )
A.刚撤去手掌瞬间,弹簧弹力等于小球重力
B.小球速度最大时,弹簧的弹性势能为零
c.弹簧的弹性势能最大时,小球速度为零
D.小球运动到最高点时,弹簧的弹性势能最大
C
