第20章 数据的整理与初步处理单元测试卷
文档属性
| 名称 | 第20章 数据的整理与初步处理单元测试卷 |  | |
| 格式 | zip | ||
| 文件大小 | 149.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-11 11:12:16 | ||
图片预览



文档简介
20章 《数据的整理与初步处理》单元测试卷
一、单选题 ?(每题3分,共27分)21世纪教育网版权所有
1.为响应“节约用水”的号召,小李随机调查了班级35名同学中5名同学家庭一年的平均用水量(单位:吨),记录如下:8,9,8,7,10,这组数据的平均数和中位数分别是(?)
A.8,8
B.8.4,8
C.8.4,8.4
D.8,8.4
2.某居民区的月底统计用电情况,其中3户用电45度,5户用电50度,6户用电42度,则平均用电为(?)21世纪教育网版权所有
A.41度
B.42度
C.45.5度
D.46度
3.七年级学生完成课题学习“从数据谈节水”后,积极践行“节约用水,从我做起”,下表是从七年级400名学生中选出10名学生统计各自家庭一个月的节水情况:
节水量(m3)
0.2
0.25
0.3
0.4
0.5
家庭数(个)
1
2
2
4
1
那么这组数据的众数和平均数分别是 A.0.4和0.34?????? B.0.4和0.3??????C.0.25和0.34?????? D.0.25和0.3
4.在某校“我的中国梦”演讲比赛中,有9名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的(???)21世纪教育网版权所有
A.众数
B.中位数
C.平均数
D.方差
5.已知一组数据2,1,x,7,3,5,3,2的众数是2,则这组数据的中位数是(?????)
A.2
B.2.5
C.3
D.5
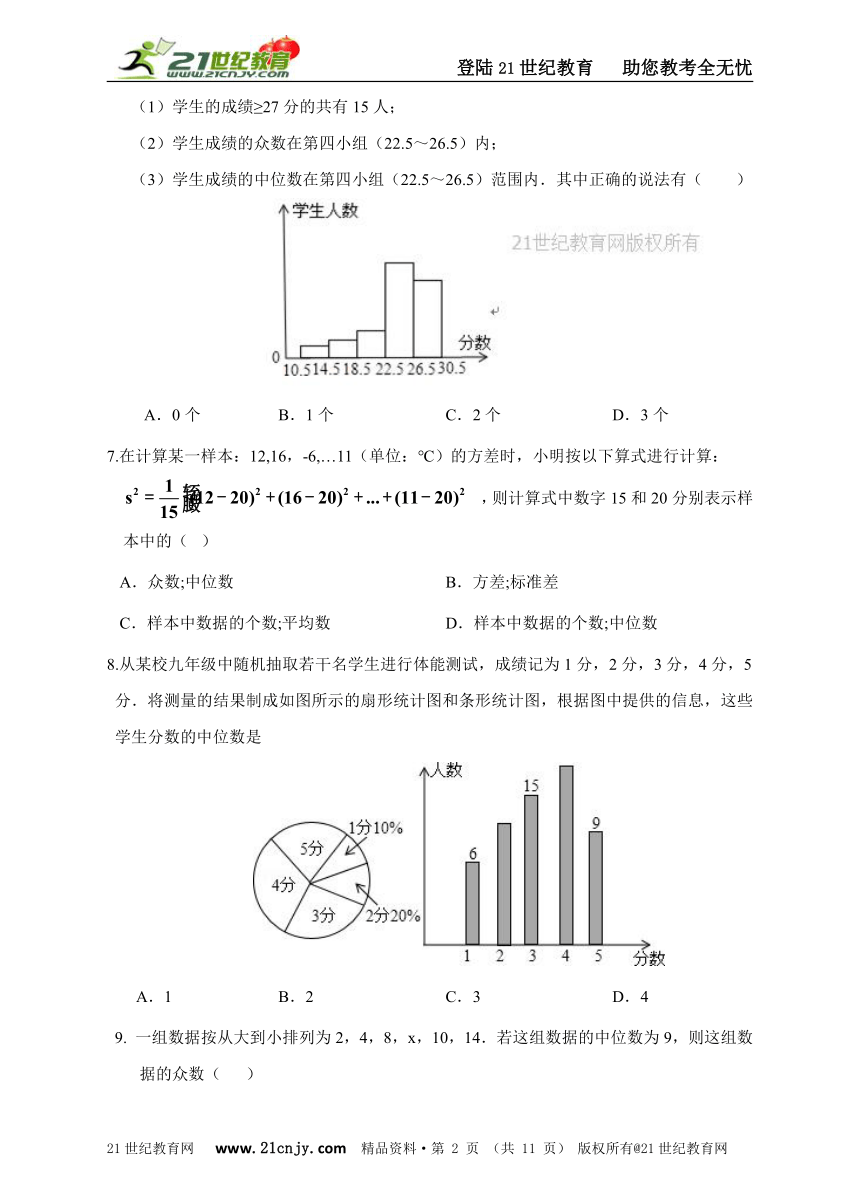
6.某校为了了解学生的身体素质情况,对初三(2)班的50名学生进行了立定跳远、铅球、100米三个项目的测试,每个项目满分为10分.如图,是将该学生所得的三项成绩(成绩均为整数)之和进行整理后,分成5组画出的频数分布直方图,已知从左至右前4个小组的频率分别为0.02,0.1,0.12,0.46. 下列说法: (1)学生的成绩≥27分的共有15人;21世纪教育网版权所有 (2)学生成绩的众数在第四小组(22.5~26.5)内; (3)学生成绩的中位数在第四小组(22.5~26.5)范围内.其中正确的说法有( )
A.0个
B.1个
C.2个
D.3个
7.在计算某一样本:12,16,-6,…11(单位:℃)的方差时,小明按以下算式进行计算:
,则计算式中数字15和20分别表示样本中的(???)21世纪教育网版权所有
A.众数;中位数
B.方差;标准差
C.样本中数据的个数;平均数
D.样本中数据的个数;中位数
8.从某校九年级中随机抽取若干名学生进行体能测试,成绩记为1分,2分,3分,4分,5
分.将测量的结果制成如图所示的扇形统计图和条形统计图,根据图中提供的信息,这些学生分数的中位数是
A.1
B.2
C.3
D.4
9. 一组数据按从大到小排列为2,4,8,x,10,14.若这组数据的中位数为9,则这组数
据的众数( )
A.6
B.8
C.9
D.10
二、填空题 ?(每题3分,共6题18分)
10. 要了解某地农户用电情况,抽查了部分农户在某地一个月中用电情况:用电15度的有3户,用电20度的有5户,用电30度的有2户,那么平均每户用电?????????
11. 若一组数据15, , 11, , 7的平均数为6,则的值是?????????
12. 某超市招聘收银员一名,对三名应聘者进行了三项素质测试.下面是三名应聘者的素质测试成绩:21世纪教育网版权所有
素质测试
测试成绩
小李
小张
小赵
计 算 机
70
90
65
商品知识
50
75
55
语???言
80
35
80
公司根据实际需要, 对计算机、商品知识、语言三项测试成绩分别赋予权重4、3、2,则这三人中???????将被录用
13.某校对甲、乙两名跳高运动员的近期跳高成绩进行统计分析,结果如下:甲=1.69m。乙=1.69m,s?甲2=0.0006,s?乙2=0.0315,则这两名运动员中的???????的成绩更稳定.
14.有个数由小到大依次排列,其平均数是 , 如果这组数的前个数的平均数是 , 后个数的平均数是 , 则这个数的中位数是_______
15. 一组数据3,4,6,8,x的中位数是x,且x是满足不等式组的整数,则这组数据的平均数是 ? .
三、解答题 ?(共5题55分)
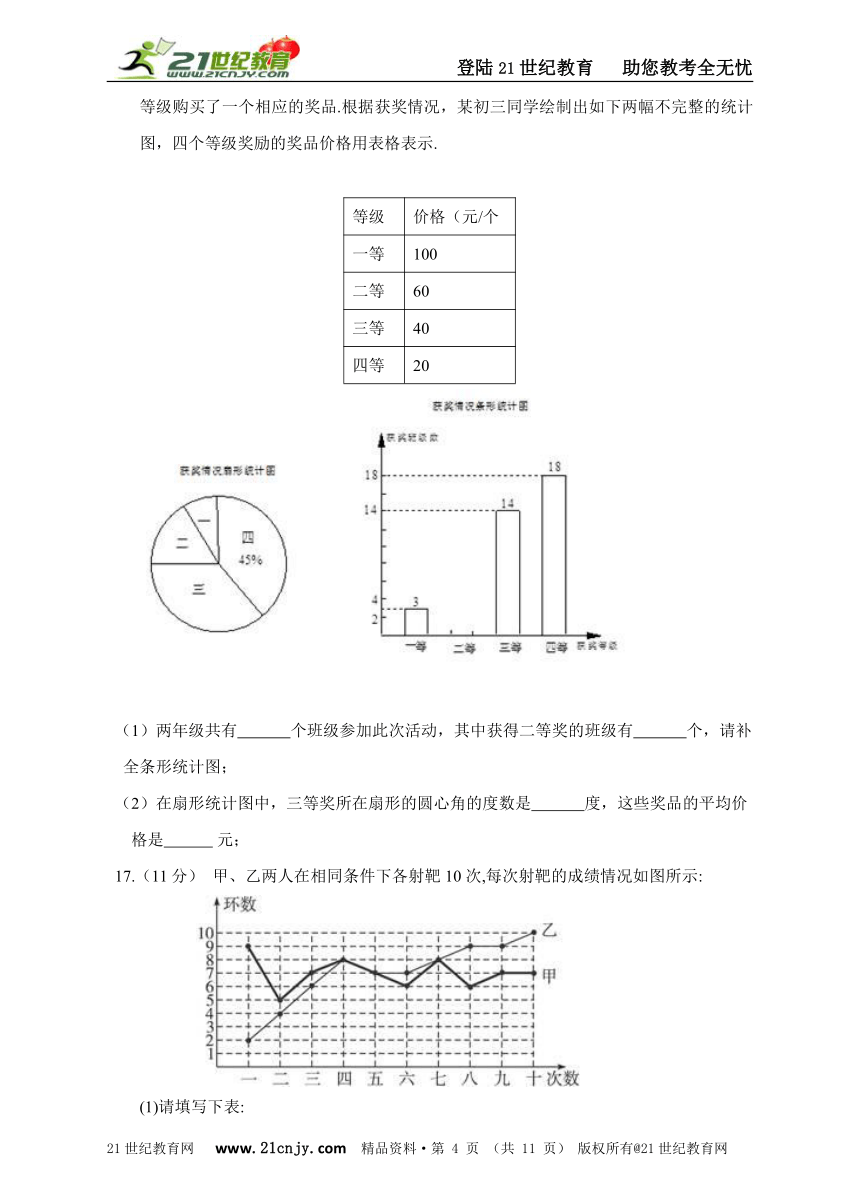
16. (10分)重庆一中注重对学生的综合素质培养,每期都将开展丰富多彩的课外活动.3月中旬,在满园的樱花树下,初一、二年级举行了“让我们一起静听花开的声音”大型诗歌朗诵会,年级各班级积极参与.学校为鼓励同学们的积极性,对参与班级进行了奖励,分设一、二、三、四等级奖励,在给予精神奖励的同时也给与一定的物质奖励,为各个等级购买了一个相应的奖品.根据获奖情况,某初三同学绘制出如下两幅不完整的统计图,四个等级奖励的奖品价格用表格表示.
等级
价格(元/个
一等
100
二等
60
三等
40
四等
20
? (1)两年级共有?????????????个班级参加此次活动,其中获得二等奖的班级有?????????????个,请补
全条形统计图; (2)在扇形统计图中,三等奖所在扇形的圆心角的度数是?????????????度,这些奖品的平均价
格是?????????????元;
17.(11分) 甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示:
(1)请填写下表:
?
平均数
方差
中位数
命中9环及以上的次数
甲
7
1.2
?
1
乙
?
5.4
?
?
(2)请从下列四个不同的角度对这次测试结果进行分析: ①从平均数和方差相结合看; ②从平均数和中位数相结合看(分析谁的成绩好些); ③从平均数和命中9环以上的次数相结合看(分析谁的成绩好些); ④从折线图上两人射击命中环数的走势看(分析谁更有潜力)
18. (11分)某单位欲从内部招聘管理人员一名,对甲、乙、丙三名候选人进行了笔试和面试两项测试,三人的测试成绩如下表所示:21世纪教育网版权所有
测试项目
测试成绩(分)
甲
乙
丙
笔试
75
80
90
面试
93
70
68
根据录用程序,组织200名职工对三人利用投票推荐的方式进行民主评议,三人得票率(没有弃权票,每位职工只能推荐1人)如图所示,每得一票记作1分. (1)请算出三人的民主评议得分. (2)如果根据三项测试的平均成绩确定录用人选,那么谁将被录用(精确到0.01)? (3)根据实际需要,单位将笔试、面试、民主评议三项测试得分按4:3:3的比例确定 个 人成绩,那么谁将被录用?
19. (11分)某校组织了“安全在我心中”知识竞赛活动.根据获奖同学在竞赛中的成绩制成的统计图表如下:?
根据以上图表提供的信息,解答下列问题: (1)写出表中x, y的数值; (2)请补全频数分布直方图;
(3)获奖成绩的中位数落在哪个分数段?
20. (12分)甲、乙两位同学参加奥赛班11次测验成绩分布如图所示:(单位:分)
(1)他们的平均成绩分别是多少? (2)他们测验成绩的方差、极差是多少? (3)现要从中选出一人参加比赛,历届比赛表明,成绩达到98分以上才可进入决赛,你认为应选谁参加这次比赛,为什么? (4)分析两位同学的成绩各有何特点?并对两位同学各提一条学习建议
答案与解析:
1. 答案:B 解析:试题分析:根据加权平均数的计算公式,先求出5个数的总和,再除以5即可,由加权平均数定义得:=(8+9+8+7+10)=8.4.中位数是一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数).∴中位数是按从小到大排列后第3个数,为:8 故选B. 考点:1、平均数的公式;2、中位数的定义
2. 答案:C. 解析:试题分析:平均数的计算方法是求出所有数据的和,然后除以数据的总个数.因此, 平均用电(度). 故选C. 考点:加权平均数.
3. 答案:A 解析:试题分析:众数是在一组数据中,出现次数最多的数据,这组数据中0.4出现4次,
。 故选A
4. 答案:B 解析:试题分析:根据中位数是一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数)的意义,9名学生参加决赛,想要知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的中位数.故选B. 考点:1.统计量的选择;2.中位数
5. 答案:B. 解析:试题分析:∵一组数据2,1,x,7,3,5,3,2的众数是2,∴x=2. ∵重新排列为1,2,2,2,3,3,5,7,∴中位数是. 故选B. 考点:1.众数;2.中位数
6. 答案:C
7. 答案:C
8. 答案:C 解析:试题分析:∵总人数为6÷10%=60(人), ∴2分的有60×20%=12(人),4分的有60﹣6﹣12﹣15﹣9=18(人)。 ∴第30与31个数据都是3分,这些学生分数的中位数是(3+3)÷2=3。 故选C
9. 答案:D 解析:试题分析:根据中位数为9得,(8+x)÷2=9,解得:x=10。 ∴这组数据中出现次数最多的是10,故众数为10。21世纪教育网版权所有 故选D
10. 答案:20.5度. 解析:试题分析:平均数的计算方法是求出所有用户的总用电量,然后除以总户数即可: 平均每户用电:. 考点:加权平均数.21世纪教育网版权所有
11. 答案:3
12. 答案:小张
13. 答案:甲 解析:试题分析:方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定. ∵S2甲=0.0006,S2乙=0.0315, ∴S2甲<S2乙 , ∴这两名运动员中甲的成绩更稳定. 考点:方差.
14. 答案:34
15. 答案:5。
16. 答案:(1)40,5,补图见解析;(2)126,38;(3). 解析:21世纪教育网版权所有 试题分析:(1)由四等奖班级18个,占45%可求得参加此次活动的班级数:;从而求得获得二等奖的班级数:。据此请补全条形统计图 (2)在扇形统计图中,三等奖所在扇形的圆心角的度数是度;这些奖品的平均价格是元.(1)40,5,补图如下: (2)126,38.
考点:1.扇形统计图;2.条形统计图;3.频数、频率和总量的关系;3.加权平均数;4.画树状图或列表法;
17. 答案:(1)如表
?
平均数
方差
中位数
命中9环及以上的次数
甲
7
1.2
7
1
乙
7
5.4
7.5
3
(2)①甲、乙平均成绩一样,甲方差较小,甲发挥更稳定. 21世纪教育网版权所有 ②从平均数和中位数相结合看,乙的成绩更好些. ③从平均数和命中9环以上的次数相结合看,说明乙的成绩好些. ④乙的成绩呈上升趋势,乙更有潜力.
18. 答案:(1)甲的民主评议得分为50,乙民主评议得分80,丙民主评议得分70; (2)如果根据三项测试的平均成绩确定录用人选,乙被录取; (3)根据实际需要,单位将笔试、面试、民主评议三项测试得分按4:3:3的比例确定个人成绩,那么丙将被录用. 解析:试题分析:(1)用200乘以每个人民主评议的得票率,即得所求. (2)求出每个人的平均成绩,平均成绩高的将被录取. (3)将笔试、面试、民主评议三项测试得分按4:3:3的比例,求得每个人的平均成绩,平均成绩高 的将被录取.21世纪教育网版权所有 试题解析:(1)甲的民主评议得分为200×25%=50, 乙民主评议得分200×40%=80, 丙民主评议得分200×35%=70; (2)∵甲的平均成绩为(50+75+93)÷3=72.67, 乙的平均成绩(80+80+70)÷3=76.67, 丙的平均成绩(70+90+68)÷3=76, ∴乙被录取;21世纪教育网版权所有 (3)∵甲的平均成绩(75×+93×+50×)÷3=72.9, 乙的平均成绩(80×+70×+80×)÷3=77, 丙的平均成绩(90×+68×+70×)÷3=77.4, ∴丙被录取. 19. 答案:(1)40;0.4;(2)补图见解析;(3)0.1;(4)85~90分. 解析:试题分析:(1)首先用分数在95≤x<100之间的人数÷频率得到总人数,x=总人数×0.2,y=1-各段的频率即可; (2)计算出x后即可补全图了; (3)用成绩在95分以上(含95分)的人数除以总人数即可; (4)根据中位数的定义:将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数,结合统计图可得答案.21世纪教育网版权所有 (1)20÷0.1=200, x=200×0.2=40; y=1-0.2-0.3-0.1=0.4; (2)如右图所示: (3)把所用数据从小到大排列,位置处于中间的是第100名和101名,由统计图可以看出第100名和101名成绩落在85~90分数段. 考点:1.频数(率)分布直方图;2.频数(率)分布表;3.中位数;
20. 答案:(1)甲的平均成绩为96分,乙的平均成绩为96分. (2)甲的方差为14.18,极差为10分;乙的方差为5.82,极差为7分. (3)甲,因为11次考试中甲有4次超过98分. (4)乙成绩稳定,甲有潜力等.建议:甲在今后的学习中应保持成绩稳定,乙在今后的学习中应不断努力,提高高分率. 21世纪教育网版权所有
一、单选题 ?(每题3分,共27分)21世纪教育网版权所有
1.为响应“节约用水”的号召,小李随机调查了班级35名同学中5名同学家庭一年的平均用水量(单位:吨),记录如下:8,9,8,7,10,这组数据的平均数和中位数分别是(?)
A.8,8
B.8.4,8
C.8.4,8.4
D.8,8.4
2.某居民区的月底统计用电情况,其中3户用电45度,5户用电50度,6户用电42度,则平均用电为(?)21世纪教育网版权所有
A.41度
B.42度
C.45.5度
D.46度
3.七年级学生完成课题学习“从数据谈节水”后,积极践行“节约用水,从我做起”,下表是从七年级400名学生中选出10名学生统计各自家庭一个月的节水情况:
节水量(m3)
0.2
0.25
0.3
0.4
0.5
家庭数(个)
1
2
2
4
1
那么这组数据的众数和平均数分别是 A.0.4和0.34?????? B.0.4和0.3??????C.0.25和0.34?????? D.0.25和0.3
4.在某校“我的中国梦”演讲比赛中,有9名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的(???)21世纪教育网版权所有
A.众数
B.中位数
C.平均数
D.方差
5.已知一组数据2,1,x,7,3,5,3,2的众数是2,则这组数据的中位数是(?????)
A.2
B.2.5
C.3
D.5
6.某校为了了解学生的身体素质情况,对初三(2)班的50名学生进行了立定跳远、铅球、100米三个项目的测试,每个项目满分为10分.如图,是将该学生所得的三项成绩(成绩均为整数)之和进行整理后,分成5组画出的频数分布直方图,已知从左至右前4个小组的频率分别为0.02,0.1,0.12,0.46. 下列说法: (1)学生的成绩≥27分的共有15人;21世纪教育网版权所有 (2)学生成绩的众数在第四小组(22.5~26.5)内; (3)学生成绩的中位数在第四小组(22.5~26.5)范围内.其中正确的说法有( )
A.0个
B.1个
C.2个
D.3个
7.在计算某一样本:12,16,-6,…11(单位:℃)的方差时,小明按以下算式进行计算:
,则计算式中数字15和20分别表示样本中的(???)21世纪教育网版权所有
A.众数;中位数
B.方差;标准差
C.样本中数据的个数;平均数
D.样本中数据的个数;中位数
8.从某校九年级中随机抽取若干名学生进行体能测试,成绩记为1分,2分,3分,4分,5
分.将测量的结果制成如图所示的扇形统计图和条形统计图,根据图中提供的信息,这些学生分数的中位数是
A.1
B.2
C.3
D.4
9. 一组数据按从大到小排列为2,4,8,x,10,14.若这组数据的中位数为9,则这组数
据的众数( )
A.6
B.8
C.9
D.10
二、填空题 ?(每题3分,共6题18分)
10. 要了解某地农户用电情况,抽查了部分农户在某地一个月中用电情况:用电15度的有3户,用电20度的有5户,用电30度的有2户,那么平均每户用电?????????
11. 若一组数据15, , 11, , 7的平均数为6,则的值是?????????
12. 某超市招聘收银员一名,对三名应聘者进行了三项素质测试.下面是三名应聘者的素质测试成绩:21世纪教育网版权所有
素质测试
测试成绩
小李
小张
小赵
计 算 机
70
90
65
商品知识
50
75
55
语???言
80
35
80
公司根据实际需要, 对计算机、商品知识、语言三项测试成绩分别赋予权重4、3、2,则这三人中???????将被录用
13.某校对甲、乙两名跳高运动员的近期跳高成绩进行统计分析,结果如下:甲=1.69m。乙=1.69m,s?甲2=0.0006,s?乙2=0.0315,则这两名运动员中的???????的成绩更稳定.
14.有个数由小到大依次排列,其平均数是 , 如果这组数的前个数的平均数是 , 后个数的平均数是 , 则这个数的中位数是_______
15. 一组数据3,4,6,8,x的中位数是x,且x是满足不等式组的整数,则这组数据的平均数是 ? .
三、解答题 ?(共5题55分)
16. (10分)重庆一中注重对学生的综合素质培养,每期都将开展丰富多彩的课外活动.3月中旬,在满园的樱花树下,初一、二年级举行了“让我们一起静听花开的声音”大型诗歌朗诵会,年级各班级积极参与.学校为鼓励同学们的积极性,对参与班级进行了奖励,分设一、二、三、四等级奖励,在给予精神奖励的同时也给与一定的物质奖励,为各个等级购买了一个相应的奖品.根据获奖情况,某初三同学绘制出如下两幅不完整的统计图,四个等级奖励的奖品价格用表格表示.
等级
价格(元/个
一等
100
二等
60
三等
40
四等
20
? (1)两年级共有?????????????个班级参加此次活动,其中获得二等奖的班级有?????????????个,请补
全条形统计图; (2)在扇形统计图中,三等奖所在扇形的圆心角的度数是?????????????度,这些奖品的平均价
格是?????????????元;
17.(11分) 甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示:
(1)请填写下表:
?
平均数
方差
中位数
命中9环及以上的次数
甲
7
1.2
?
1
乙
?
5.4
?
?
(2)请从下列四个不同的角度对这次测试结果进行分析: ①从平均数和方差相结合看; ②从平均数和中位数相结合看(分析谁的成绩好些); ③从平均数和命中9环以上的次数相结合看(分析谁的成绩好些); ④从折线图上两人射击命中环数的走势看(分析谁更有潜力)
18. (11分)某单位欲从内部招聘管理人员一名,对甲、乙、丙三名候选人进行了笔试和面试两项测试,三人的测试成绩如下表所示:21世纪教育网版权所有
测试项目
测试成绩(分)
甲
乙
丙
笔试
75
80
90
面试
93
70
68
根据录用程序,组织200名职工对三人利用投票推荐的方式进行民主评议,三人得票率(没有弃权票,每位职工只能推荐1人)如图所示,每得一票记作1分. (1)请算出三人的民主评议得分. (2)如果根据三项测试的平均成绩确定录用人选,那么谁将被录用(精确到0.01)? (3)根据实际需要,单位将笔试、面试、民主评议三项测试得分按4:3:3的比例确定 个 人成绩,那么谁将被录用?
19. (11分)某校组织了“安全在我心中”知识竞赛活动.根据获奖同学在竞赛中的成绩制成的统计图表如下:?
根据以上图表提供的信息,解答下列问题: (1)写出表中x, y的数值; (2)请补全频数分布直方图;
(3)获奖成绩的中位数落在哪个分数段?
20. (12分)甲、乙两位同学参加奥赛班11次测验成绩分布如图所示:(单位:分)
(1)他们的平均成绩分别是多少? (2)他们测验成绩的方差、极差是多少? (3)现要从中选出一人参加比赛,历届比赛表明,成绩达到98分以上才可进入决赛,你认为应选谁参加这次比赛,为什么? (4)分析两位同学的成绩各有何特点?并对两位同学各提一条学习建议
答案与解析:
1. 答案:B 解析:试题分析:根据加权平均数的计算公式,先求出5个数的总和,再除以5即可,由加权平均数定义得:=(8+9+8+7+10)=8.4.中位数是一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数).∴中位数是按从小到大排列后第3个数,为:8 故选B. 考点:1、平均数的公式;2、中位数的定义
2. 答案:C. 解析:试题分析:平均数的计算方法是求出所有数据的和,然后除以数据的总个数.因此, 平均用电(度). 故选C. 考点:加权平均数.
3. 答案:A 解析:试题分析:众数是在一组数据中,出现次数最多的数据,这组数据中0.4出现4次,
。 故选A
4. 答案:B 解析:试题分析:根据中位数是一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数)的意义,9名学生参加决赛,想要知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的中位数.故选B. 考点:1.统计量的选择;2.中位数
5. 答案:B. 解析:试题分析:∵一组数据2,1,x,7,3,5,3,2的众数是2,∴x=2. ∵重新排列为1,2,2,2,3,3,5,7,∴中位数是. 故选B. 考点:1.众数;2.中位数
6. 答案:C
7. 答案:C
8. 答案:C 解析:试题分析:∵总人数为6÷10%=60(人), ∴2分的有60×20%=12(人),4分的有60﹣6﹣12﹣15﹣9=18(人)。 ∴第30与31个数据都是3分,这些学生分数的中位数是(3+3)÷2=3。 故选C
9. 答案:D 解析:试题分析:根据中位数为9得,(8+x)÷2=9,解得:x=10。 ∴这组数据中出现次数最多的是10,故众数为10。21世纪教育网版权所有 故选D
10. 答案:20.5度. 解析:试题分析:平均数的计算方法是求出所有用户的总用电量,然后除以总户数即可: 平均每户用电:. 考点:加权平均数.21世纪教育网版权所有
11. 答案:3
12. 答案:小张
13. 答案:甲 解析:试题分析:方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定. ∵S2甲=0.0006,S2乙=0.0315, ∴S2甲<S2乙 , ∴这两名运动员中甲的成绩更稳定. 考点:方差.
14. 答案:34
15. 答案:5。
16. 答案:(1)40,5,补图见解析;(2)126,38;(3). 解析:21世纪教育网版权所有 试题分析:(1)由四等奖班级18个,占45%可求得参加此次活动的班级数:;从而求得获得二等奖的班级数:。据此请补全条形统计图 (2)在扇形统计图中,三等奖所在扇形的圆心角的度数是度;这些奖品的平均价格是元.(1)40,5,补图如下: (2)126,38.
考点:1.扇形统计图;2.条形统计图;3.频数、频率和总量的关系;3.加权平均数;4.画树状图或列表法;
17. 答案:(1)如表
?
平均数
方差
中位数
命中9环及以上的次数
甲
7
1.2
7
1
乙
7
5.4
7.5
3
(2)①甲、乙平均成绩一样,甲方差较小,甲发挥更稳定. 21世纪教育网版权所有 ②从平均数和中位数相结合看,乙的成绩更好些. ③从平均数和命中9环以上的次数相结合看,说明乙的成绩好些. ④乙的成绩呈上升趋势,乙更有潜力.
18. 答案:(1)甲的民主评议得分为50,乙民主评议得分80,丙民主评议得分70; (2)如果根据三项测试的平均成绩确定录用人选,乙被录取; (3)根据实际需要,单位将笔试、面试、民主评议三项测试得分按4:3:3的比例确定个人成绩,那么丙将被录用. 解析:试题分析:(1)用200乘以每个人民主评议的得票率,即得所求. (2)求出每个人的平均成绩,平均成绩高的将被录取. (3)将笔试、面试、民主评议三项测试得分按4:3:3的比例,求得每个人的平均成绩,平均成绩高 的将被录取.21世纪教育网版权所有 试题解析:(1)甲的民主评议得分为200×25%=50, 乙民主评议得分200×40%=80, 丙民主评议得分200×35%=70; (2)∵甲的平均成绩为(50+75+93)÷3=72.67, 乙的平均成绩(80+80+70)÷3=76.67, 丙的平均成绩(70+90+68)÷3=76, ∴乙被录取;21世纪教育网版权所有 (3)∵甲的平均成绩(75×+93×+50×)÷3=72.9, 乙的平均成绩(80×+70×+80×)÷3=77, 丙的平均成绩(90×+68×+70×)÷3=77.4, ∴丙被录取. 19. 答案:(1)40;0.4;(2)补图见解析;(3)0.1;(4)85~90分. 解析:试题分析:(1)首先用分数在95≤x<100之间的人数÷频率得到总人数,x=总人数×0.2,y=1-各段的频率即可; (2)计算出x后即可补全图了; (3)用成绩在95分以上(含95分)的人数除以总人数即可; (4)根据中位数的定义:将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数,结合统计图可得答案.21世纪教育网版权所有 (1)20÷0.1=200, x=200×0.2=40; y=1-0.2-0.3-0.1=0.4; (2)如右图所示: (3)把所用数据从小到大排列,位置处于中间的是第100名和101名,由统计图可以看出第100名和101名成绩落在85~90分数段. 考点:1.频数(率)分布直方图;2.频数(率)分布表;3.中位数;
20. 答案:(1)甲的平均成绩为96分,乙的平均成绩为96分. (2)甲的方差为14.18,极差为10分;乙的方差为5.82,极差为7分. (3)甲,因为11次考试中甲有4次超过98分. (4)乙成绩稳定,甲有潜力等.建议:甲在今后的学习中应保持成绩稳定,乙在今后的学习中应不断努力,提高高分率. 21世纪教育网版权所有
