点到直线的距离

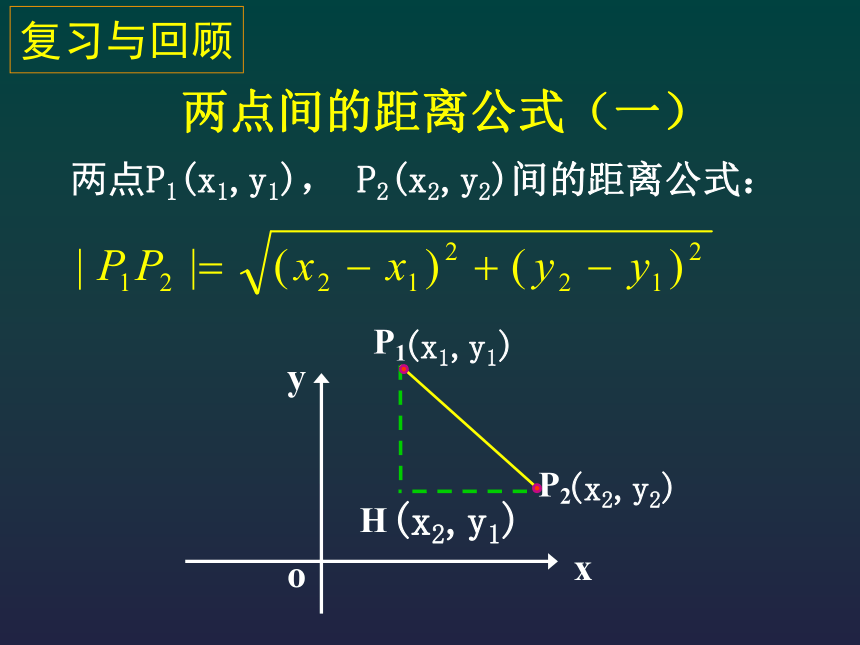
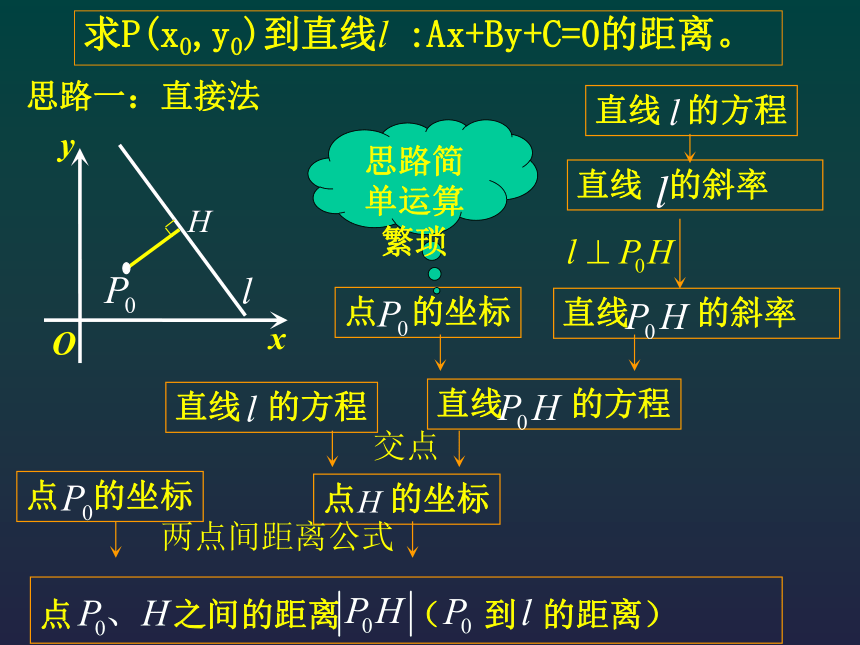
课件15张PPT。点到直线的距离授课人：洪伟荣授课地点：高一（14）班两点间的距离公式（一）复习与回顾两点P1(x1,y1)， P2(x2,y2)间的距离公式：两点间的距离（二）复习与回顾两点间的距离公式中特别的情况：两点P1(x1,y1)， P2(x2,y2)间的距离公式：思考：如图，已知点P和直线 l ，请你说出如何作出表示点P到直线 l 的距离的线段。PlH我们发现“点到直线的距离就是从直线外一点到这条直线的垂线段长度”。 点到直线的距离 点到直线的距离：从直线外一点到这条直线的垂线段长度。练习1：求下列点到直线的距离（1）P1（1，2）， l1 ：x＝－3； （2）O（0，0）， l2 ：2x＋3y－6＝0； （3）P3（2，3）， l3 ：2x＋3y－6＝0； 试一试点到直线的距离思路一：直接法xyO思路简单运算繁琐求P(x0,y0)到直线l :Ax+By+C=0的距离。思路二：间接法xyO求P(x0,y0)到直线l :Ax+By+C=0的距离。SR求P(x0,y0)到直线l :Ax+By+C=0的距离。H设S(n,y0)，R(x0,m)|PS|=|X0-n|,|PR|=|y0-m|因为，S,R均在l上所以,An+By0+C=0,Ax0+Bm+C=0所以所以(n,y0)(x0,m)点P(x0,y0)到直线l :Ax+By+C=0的距离公式所以我们必须注意：利用点到直线的距离公式时，必须注意先把直线方程化成一般式。公式特点：（1）公式的分子部分绝对值里面的式子与直线的一般式方程等式左边部分形式相同；（2）公式的分母部分根号里面是直线一般式形式中的x，y的系数的平方和；解：把直线 l 的方程化为一般式得 3x－2＝0,所以，点P0到直线 l 的距离为：思考：还有其他解法吗？典型例题所以，点P0到直线 l 的距离为：典型例题因此，典型例题思考：还有其他解法吗？因此，典型例题D令y＝0，解得D（4，0）=5练习1.求坐标原点到下列直线的距离：(1) 3x+2y-26=0; (2) x=y2.求下列点到直线的距离：(1) A(-2,3)， 3x+4y+3=0(3) C(1,-2)， 4x+3y=0P108 练习作业：P109—P110
5、7、8、9