第五章《圆》阶段性测试(第五章第5、6节)(含答案)
文档属性
| 名称 | 第五章《圆》阶段性测试(第五章第5、6节)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-11 21:06:02 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
阶段性测试
(考查范围:第五章第5~6节 时间:45分钟 满分:100分)
一、选择题(每小题5分,共40分)
1.下列条件中,能确定一个圆的是( )
A.经过已知点 M B.以点O为圆心,10cm长为半径
C.以10cm长为半径 D.以点O为圆心
的外心在三角形的一边上,则 是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法判断
3.已知⊙O 的半径r=5,圆心O到直线的距离 则直线与⊙O的位置关系为( )
A.相交 B.相切 C.相离 D.相交或相切
4.在圆内接四边形 ABCD中,∠A :∠B: ∠C=1:2:5,则∠D 的度数为( )
A.30° B.60° C.120° D.150°
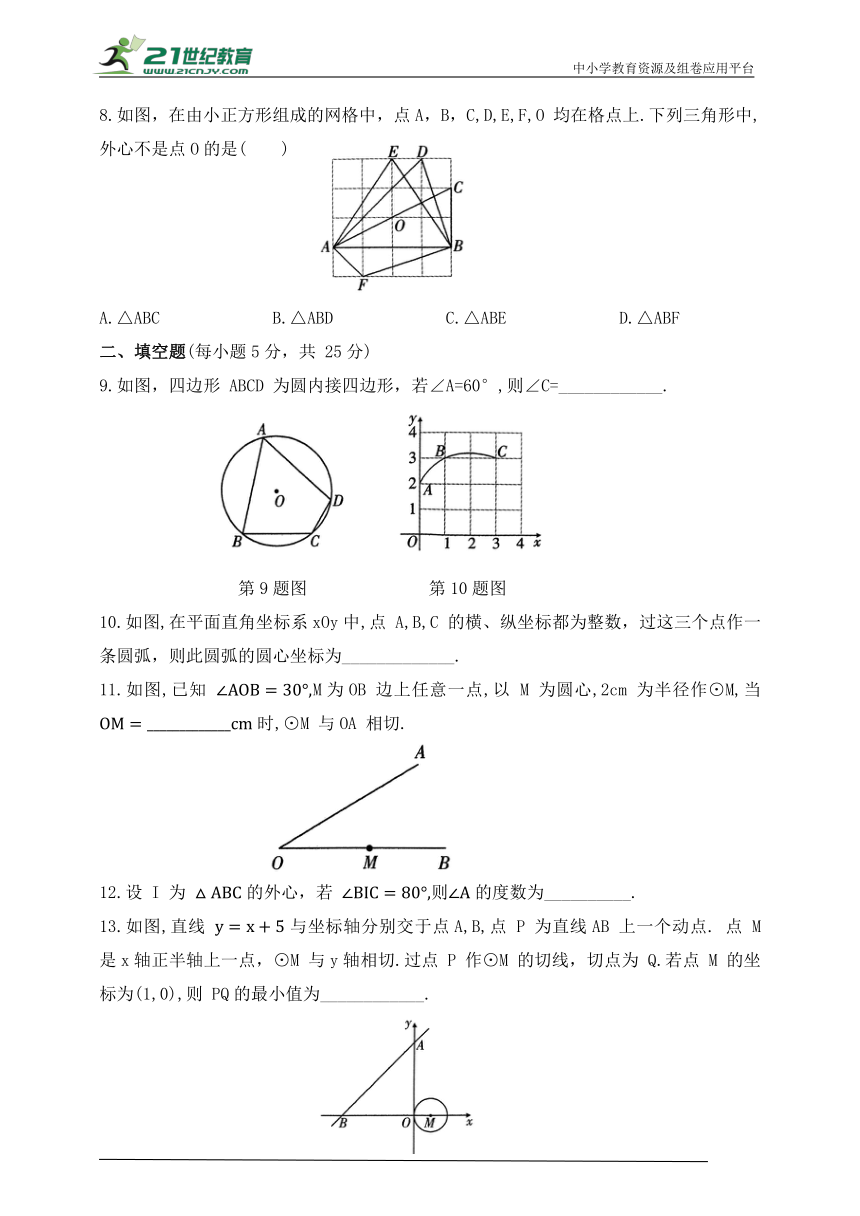
5.如图,AB 是⊙O 的切线,切点为 B,连接 AO 与⊙O 交于点 C,点 D 为弧BmC 上一点,连接BD,CD.若∠A =36°,则∠BDC 的度 数为( )
A.32° B.18° C.27° D.36°
第5题图 第 6题图
6.如图,四边形 ABCD 是⊙O 的内接四边形,点D 是 的中点,点 E 是 上的一点,若 ,则∠DEC 的度数是( )
A.35° B.45° C.50° D.55°
7.如图,⊙O 是△ABC的内切圆,切点分别为D,E,F,且 则⊙O 的半径是( )
A.1 C.2
8.如图,在由小正方形组成的网格中,点A,B,C,D,E,F,O 均在格点上.下列三角形中,外心不是点O的是( )
A.△ABC B.△ABD C.△ABE D.△ABF
二、填空题(每小题5分,共 25分)
9.如图,四边形 ABCD 为圆内接四边形,若∠A=60°,则∠C=____________.
第9题图 第10题图
10.如图,在平面直角坐标系xOy中,点 A,B,C 的横、纵坐标都为整数,过这三个点作一条圆弧,则此圆弧的圆心坐标为_____________.
11.如图,已知 M为OB 边上任意一点,以 M 为圆心,2cm 为半径作⊙M,当时,⊙M 与OA 相切.
12.设 I 为 的外心,若 则的度数为__________.
13.如图,直线 与坐标轴分别交于点A,B,点 P 为直线AB 上一个动点. 点 M 是x轴正半轴上一点,⊙M 与y轴相切.过点 P 作⊙M 的切线,切点为 Q.若点 M 的坐标为(1,0),则 PQ的最小值为____________.
三、解答题(共35分)
14.(10分)如图, 内接于⊙O, D 是圆上任一点.求证:DA 平分
15.(12 分)如图, 中, 过A,B 两点的⊙O 交 AC 于点 D,且 ∥BC,OD 交AB 于点E.
(1)求证:BC 是⊙O 的切线.
(2)若 求AD:CD的值.
16.(13分)阅读材料,解答问题.
关于圆的引理
古希腊数学家、物理学家阿基米德流传于世的数学著作有10余种,下面是《阿基米德全集》的《引理集》中记载的一个命题:
如图①,AB 是⊙O 的弦,点 C 在⊙O上,CD⊥AB 于点 D,在弦 AB 上取点E,使DE=AD,点 F 是. 上的一点,且 连接 BF,则 BF=BE.
小颖对这个问题很感兴趣,经过思考,写出了下面的证明过程:
证明:如图②,连接CA,CE,CF,BC.
∵CD⊥AB 于点D,DE=AD,∴CA=CE,∴∠CAE=∠CEA.
∴CF=CA(依据1),∠CBF=∠CBA.
∵四边形 ABFC 内接于⊙O, (依据2)
……
(1)上述证明过程中的依据1为_______________________________________________,依据2 为__________________________________________________.
(2)将上述证明过程补充完整.
参考答案
1. B 2. B 3. A 4. C 5. C 6. A 7. C 8. C
10.(2,1) 11.4 12.40°或140°
14. 证 明:
平分
15.(1)证 明: 如图,连 接 OB.
∴
∴BC是⊙O 的切线.
(2)解:连接
∥
16.(1)在同圆中相等的弧所对的弦相等 圆内接四边形的对角互补
(2)证明:如图②,连接CA,CE,CF,BC.
∵CD⊥AB 于点 D,
∴CF=CA,∴∠CBF=∠CBA.
∵四边形 ABFC内接于⊙O,
在和 中,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
阶段性测试
(考查范围:第五章第5~6节 时间:45分钟 满分:100分)
一、选择题(每小题5分,共40分)
1.下列条件中,能确定一个圆的是( )
A.经过已知点 M B.以点O为圆心,10cm长为半径
C.以10cm长为半径 D.以点O为圆心
的外心在三角形的一边上,则 是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法判断
3.已知⊙O 的半径r=5,圆心O到直线的距离 则直线与⊙O的位置关系为( )
A.相交 B.相切 C.相离 D.相交或相切
4.在圆内接四边形 ABCD中,∠A :∠B: ∠C=1:2:5,则∠D 的度数为( )
A.30° B.60° C.120° D.150°
5.如图,AB 是⊙O 的切线,切点为 B,连接 AO 与⊙O 交于点 C,点 D 为弧BmC 上一点,连接BD,CD.若∠A =36°,则∠BDC 的度 数为( )
A.32° B.18° C.27° D.36°
第5题图 第 6题图
6.如图,四边形 ABCD 是⊙O 的内接四边形,点D 是 的中点,点 E 是 上的一点,若 ,则∠DEC 的度数是( )
A.35° B.45° C.50° D.55°
7.如图,⊙O 是△ABC的内切圆,切点分别为D,E,F,且 则⊙O 的半径是( )
A.1 C.2
8.如图,在由小正方形组成的网格中,点A,B,C,D,E,F,O 均在格点上.下列三角形中,外心不是点O的是( )
A.△ABC B.△ABD C.△ABE D.△ABF
二、填空题(每小题5分,共 25分)
9.如图,四边形 ABCD 为圆内接四边形,若∠A=60°,则∠C=____________.
第9题图 第10题图
10.如图,在平面直角坐标系xOy中,点 A,B,C 的横、纵坐标都为整数,过这三个点作一条圆弧,则此圆弧的圆心坐标为_____________.
11.如图,已知 M为OB 边上任意一点,以 M 为圆心,2cm 为半径作⊙M,当时,⊙M 与OA 相切.
12.设 I 为 的外心,若 则的度数为__________.
13.如图,直线 与坐标轴分别交于点A,B,点 P 为直线AB 上一个动点. 点 M 是x轴正半轴上一点,⊙M 与y轴相切.过点 P 作⊙M 的切线,切点为 Q.若点 M 的坐标为(1,0),则 PQ的最小值为____________.
三、解答题(共35分)
14.(10分)如图, 内接于⊙O, D 是圆上任一点.求证:DA 平分
15.(12 分)如图, 中, 过A,B 两点的⊙O 交 AC 于点 D,且 ∥BC,OD 交AB 于点E.
(1)求证:BC 是⊙O 的切线.
(2)若 求AD:CD的值.
16.(13分)阅读材料,解答问题.
关于圆的引理
古希腊数学家、物理学家阿基米德流传于世的数学著作有10余种,下面是《阿基米德全集》的《引理集》中记载的一个命题:
如图①,AB 是⊙O 的弦,点 C 在⊙O上,CD⊥AB 于点 D,在弦 AB 上取点E,使DE=AD,点 F 是. 上的一点,且 连接 BF,则 BF=BE.
小颖对这个问题很感兴趣,经过思考,写出了下面的证明过程:
证明:如图②,连接CA,CE,CF,BC.
∵CD⊥AB 于点D,DE=AD,∴CA=CE,∴∠CAE=∠CEA.
∴CF=CA(依据1),∠CBF=∠CBA.
∵四边形 ABFC 内接于⊙O, (依据2)
……
(1)上述证明过程中的依据1为_______________________________________________,依据2 为__________________________________________________.
(2)将上述证明过程补充完整.
参考答案
1. B 2. B 3. A 4. C 5. C 6. A 7. C 8. C
10.(2,1) 11.4 12.40°或140°
14. 证 明:
平分
15.(1)证 明: 如图,连 接 OB.
∴
∴BC是⊙O 的切线.
(2)解:连接
∥
16.(1)在同圆中相等的弧所对的弦相等 圆内接四边形的对角互补
(2)证明:如图②,连接CA,CE,CF,BC.
∵CD⊥AB 于点 D,
∴CF=CA,∴∠CBF=∠CBA.
∵四边形 ABFC内接于⊙O,
在和 中,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
