6.2 向心力 课件(共31张PPT) -2023-2024学年高一下学期物理人教版(2019)必修第二册
文档属性
| 名称 | 6.2 向心力 课件(共31张PPT) -2023-2024学年高一下学期物理人教版(2019)必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-01-10 21:13:31 | ||
图片预览









文档简介
(共31张PPT)
第六章 圆周运动
第2节 向心力
一、向心力
二、向心加速度
三、匀速圆周运动
四、变速圆周运动
第2节 向心力
五、一般曲线运动
摩天轮里的人为什么能做匀速圆周运动?
圆周运动的速度方向一直变化,则人合力肯定不为零。
问题与思考:
1.恒力跟初速度共线:
匀变速直线
类平抛运动
2.恒力跟初速度垂直:
3.什么样的受力能决定物体做匀速圆周?
做圆周运动的人受力有什么特点能决定它做圆周运动
mg
N
O
T
在光滑水平面上,轻绳一端固定,另一端栓一球使球做匀速圆周运动,分析小球的受力特点
mg
N
T
mg
N
T
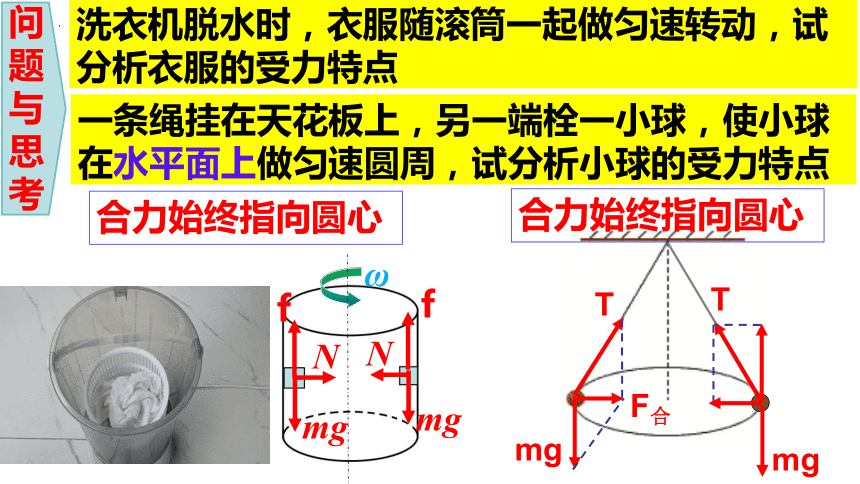
合力始终指向圆心
mg
N
f
mg
N
f
合力始终指向圆心
一物体在粗糙的水平转盘上,跟着转盘一起做匀速圆周运动,分析小物体的受力特点
问
题
与
思
考
ω
mg
f
N
洗衣机脱水时,衣服随滚筒一起做匀速转动,试分析衣服的受力特点
mg
f
N
问
题
与
思
考
合力始终指向圆心
一条绳挂在天花板上,另一端栓一小球,使小球在水平面上做匀速圆周,试分析小球的受力特点
mg
T
F合
mg
T
合力始终指向圆心
mg
N
O
T
mg
N
T
mg
N
T
mg
N
f
mg
N
f
ω
mg
f
N
mg
f
N
做匀速圆周物体的受力特点是合力必须始终指向圆心
我们把这合力又叫做向心力
mg
T
F合
mg
T
【典例1】如图,小物体m与圆盘保持相对静止,随盘一起做匀速圆周运动,则物体的受力情况是( )
A.受重力、支持力、静摩擦力和向心力的作用
B.摩擦力的方向始终指向圆心O
C.重力和支持力是一对平衡力
D.摩擦力是使物体做匀速圆周运动的向心力
BCD
【变式1】在水平面上,小猴拉着小滑块做匀速圆周运动,O点为圆心,能正确地表示小滑块受到的牵引力及摩擦力Ff的图是( )
A
指向圆心的力
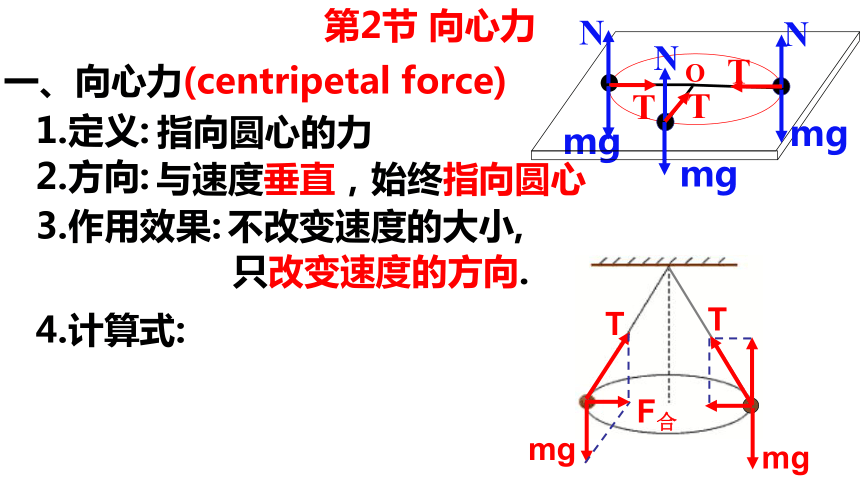
3.作用效果:
一、向心力(centripetal force)
2.方向:
1.定义:
与速度垂直,始终指向圆心
只改变速度的方向.
不改变速度的大小,
4.计算式:
第2节 向心力
mg
N
O
T
mg
N
T
mg
N
T
mg
T
F合
mg
T
体验与猜测:
向心力大小的影响因素
实验方法
1.F与m的关系:
保持r、ω一定
2.F与r的关系:
保持m、ω一定
3.F与ω的关系:
保持r、m一定
结论: F∝m
结论: F∝r
结论: F∝ω2
F向与
ω有关
m、
r 、
控制变量法
F向=kmω2r
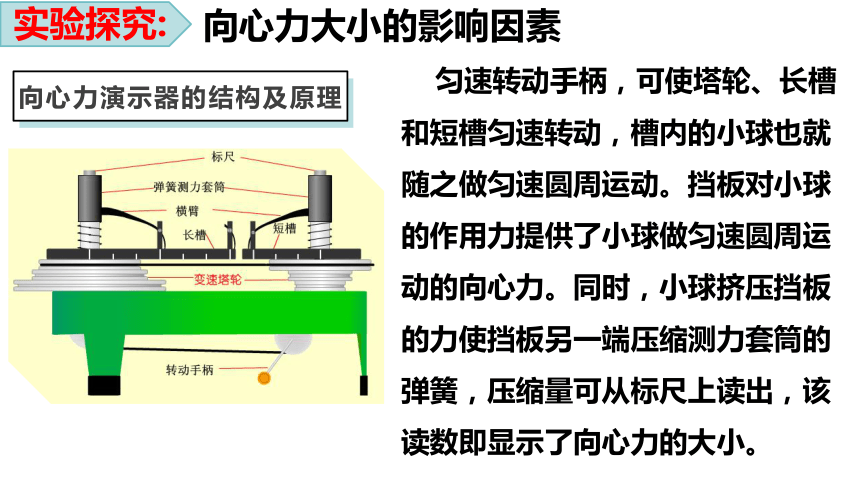
实验探究:
匀速转动手柄,可使塔轮、长槽和短槽匀速转动,槽内的小球也就随之做匀速圆周运动。挡板对小球的作用力提供了小球做匀速圆周运动的向心力。同时,小球挤压挡板的力使挡板另一端压缩测力套筒的弹簧,压缩量可从标尺上读出,该读数即显示了向心力的大小。
向心力演示器的结构及原理
向心力大小的影响因素
实验探究:
4π2
T2
m
r
F向=mω2r
5.变式:
指向圆心的力
3.作用效果:
一、向心力(centripetal force)
2.方向:
1.定义:
与速度垂直,始终指向圆心
只改变速度的方向.
不改变速度的大小.
4.计算式:
第2节 向心力
F向=
v2
r
m
=
mωv
=
v=ωr
注意:向心力不是一种新的力,它是一种效果力。
2π
T
ω=
地球为什么围着太阳旋转
探究向心力的来源:
F引=F向
F引
=mω2r
O
r
ω
m
探究向心力的来源:
小球在光滑玻璃漏斗中某一平面内做匀速圆周运动
重力和支持力的合力充当F向
竖直方向:
水平方向:
θ
θ
mg
N
Ncosθ=mg
Nsinθ=mω2r
F合=F向
mgtanθ
mg
N
F合
=mω2r
mgtanθ
=mω2r
gtanθ=ω2r
ω=
【典例2】(多选)如图所示,一个内壁光滑的圆锥形筒的轴线垂直于水平面,圆锥形筒固定不动,有两个质量相等的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则下列说法正确的是( )
A. 线速度A球大于B球
B. 角速度A球小于B球
C. 周期A球小于B球
D. 对筒壁的压力A球大于B球
mg
NA
mg
NB
A
B
AB
θ
mgtanθ=
=mω2r
v2
r
m
=m
4π2
T2
r
V=
ω=
T=
【变式2】(多选)如图所示,一个内壁光滑的圆锥形筒的轴线垂直于水平面,圆锥形筒固定不动,有两个小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,其中mA>mB , 则下列说法正确的是( )
A. 线速度A球大于B球
B. 角速度A球小于B球
C. 周期A球小于B球
D. 对筒壁的压力A球大于B球
mg
NA
mg
NB
A
B
ABD
θ
mgtanθ=
=mω2r
v2
r
m
=m
4π2
T2
r
V=
ω=
T=
【典例3】一根长为L=2.5 m的轻绳两端分别固定在一根竖直棒上的A、B两点,一个质量为m=0.6 kg的光滑小圆环套在绳子上,当竖直棒以一定的角速度转动时,圆环以B为圆心在水平面上做匀速圆周运动,(θ=37°,g=10 m/s2)则此时轻绳上的张力T和竖直棒转动的角速度ω各为多大( )
A.T=10N
B.T=7.5N
C.ω=3
D.ω=3
mg
T
T
mg=
Tsin370
得T=
10N
T+
Tcos370
=mω2r
r+
r
cos370
=L
得ω=
AC
3
【典例4】两根长度不同的细线下面分别悬挂两个相同小球,细线上端固定在同一点,若两个小球以相同的角速度绕共同的竖直轴在水平面内做匀速圆周运动,则两个摆球在运动过程中,相对位置关系示意图正确的是( )
B
mgtanθ=
mω2r
mg
T
θ
=mω2Lsinθ
θ
L
ω=
二、向心加速度
1.定义:
2.大小:
向心力产生的加速度,
3.方向:
a向=
F向
m
=
v2
r
=
ω2r
=
4π2
T2
r
方向总指向圆心
4.物理意义:
描述线速度方向变化的快慢。
一、向心力:
F向=
v2
r
m
=
mω2r
=
4π2
T2
m
r
=mωv
=ωv
第2节 向心力
【典例5】如图所示,一球体绕轴O1O2以角速度ω旋转,A、B为球体上两点。下列说法中正确的是( )
A. A、B两点具有相同的角速度
B. A、B两点具有相同的线速度
C. A、B两点具有相同的向心加速度
D. A、B两点的向心加速度方向都指向球心
A
三、匀速圆周运动
3.a向大小不变,
2.合力全部提供F向,
1.速度方向时刻改变,
是变速曲线.
F向大小不变,方向在变
方向时刻改变,
不是匀变速曲线运动
那变速圆周?
二、向心加速度
第2节 向心力
一、向心力
mg
T
mg
T
问题与思考:
一小球用绳栓住在竖直面内做部分圆周,
试分析小球的受力特点?
合力不再始终指向圆心
1.合力一般不等于向心力
四、变速圆周运动
2.合力中指向圆心的部分提供F向:
产生的a叫向心加速度,
3.合力中跟圆相切的部分提供切向力:
改变v的方向。
改变v的大小。
T
mg
T
mg
三、匀速圆周运动
二、向心加速度
第2节 向心力
一、向心力
产生的a叫切向加速度,
θ
T-mgcosθ=F向
=m
v2
r
mgsinθ=F切
=ma切
T-mgcosθ=ma向
【典例6】如图所示,一质量为m的木块从光滑的半球形的碗边开始下滑,在木块下滑过程中( )
A.它的加速度方向指向球心
B.它所受合力就是向心力
C.它所受向心力不断增大
D.它对碗的压力不断减小
C
mg
N
N
mg
【典例7】如图所示,汽车减速经过水平弯路
(可看做圆形轨道的一部分),关于汽车向心力
及合外力的分析正确的是( )
A.汽车拐弯时向心力由汽车方向盘来提供
B.汽车拐弯时向心力由地面来提供,与线速度方向相反
C.汽车拐弯时所受合外力指向圆心方向
D.汽车拐弯时所受合外力可能指向如图虚线方向
D
五、一般曲线运动
微元为半径在时刻改变的变速圆周运动
四、变速圆周运动
三、匀速圆周运动
二、向心加速度
第2节 向心力
一、向心力
1.处理方法:
2.曲率半径:
r2
r1
每个位置内切圆的半径
【典例8】一般的曲线运动可以分成很多小段,每小段都可以看成圆周运动的一部分,即把整条曲线用一系列不同半径的小圆弧来代替。如图(a)所示,曲线上的A点的曲率圆定义为:通过A点和曲线上紧邻A点两侧的两点作一圆,在极限情况下,这个圆就叫做A点的曲率圆,其半径ρ叫做A点的曲率半径。现将一物体沿与水平面成α角的方向以速度v0抛出,如图(b)所示。则在其轨迹最高点处的曲率半径是( )
A.v02/g
B.v02sin2α/g
C.v02cos2α/g
D.v02cos2α/gsinα
C
1.(对向心加速度的理解)下列关于向心加速度的说法正确的是( )
A.向心加速度越大,物体速率变化越快
B.向心加速度越大,物体转动得越快
C.向心加速度方向始终与速度方向垂直
D.在匀速圆周运动中,向心加速度是恒定的
C
课堂练习
2.((多选)一小球被细绳拴着在水平面内做半径为R的匀速圆周运动,向心加速度为an,那么( )
ABD
课堂练习
3.(多选)如图所示的皮带传动装置,主动轮的半径与从动轮的半径之比R1∶R2=2∶1,A、B分别是两轮边缘上的点,假定皮带不打滑,则下列说法正确的是( )
A.A、B两点的线速度之比为vA∶vB=1∶2
B.A、B两点的线速度之比为vA∶vB=1∶1
C.A 、B两点的加速度之比为aA∶aB=1∶2
D.A、B两点的加速度之比为aA∶aB=2∶1
BC
课堂练习
4.如图所示,定滑轮的半径r=2 cm。绕在滑轮上的细线悬挂着一个重物,由静止开始释放,测得重物以加速度a=2 m/s2向下做匀加速运动。在重物由静止下落1 m的瞬间,滑轮边缘上P点向心加速度多大?
答案 200 m/s2
课堂练习
第六章 圆周运动
第2节 向心力
一、向心力
二、向心加速度
三、匀速圆周运动
四、变速圆周运动
第2节 向心力
五、一般曲线运动
摩天轮里的人为什么能做匀速圆周运动?
圆周运动的速度方向一直变化,则人合力肯定不为零。
问题与思考:
1.恒力跟初速度共线:
匀变速直线
类平抛运动
2.恒力跟初速度垂直:
3.什么样的受力能决定物体做匀速圆周?
做圆周运动的人受力有什么特点能决定它做圆周运动
mg
N
O
T
在光滑水平面上,轻绳一端固定,另一端栓一球使球做匀速圆周运动,分析小球的受力特点
mg
N
T
mg
N
T
合力始终指向圆心
mg
N
f
mg
N
f
合力始终指向圆心
一物体在粗糙的水平转盘上,跟着转盘一起做匀速圆周运动,分析小物体的受力特点
问
题
与
思
考
ω
mg
f
N
洗衣机脱水时,衣服随滚筒一起做匀速转动,试分析衣服的受力特点
mg
f
N
问
题
与
思
考
合力始终指向圆心
一条绳挂在天花板上,另一端栓一小球,使小球在水平面上做匀速圆周,试分析小球的受力特点
mg
T
F合
mg
T
合力始终指向圆心
mg
N
O
T
mg
N
T
mg
N
T
mg
N
f
mg
N
f
ω
mg
f
N
mg
f
N
做匀速圆周物体的受力特点是合力必须始终指向圆心
我们把这合力又叫做向心力
mg
T
F合
mg
T
【典例1】如图,小物体m与圆盘保持相对静止,随盘一起做匀速圆周运动,则物体的受力情况是( )
A.受重力、支持力、静摩擦力和向心力的作用
B.摩擦力的方向始终指向圆心O
C.重力和支持力是一对平衡力
D.摩擦力是使物体做匀速圆周运动的向心力
BCD
【变式1】在水平面上,小猴拉着小滑块做匀速圆周运动,O点为圆心,能正确地表示小滑块受到的牵引力及摩擦力Ff的图是( )
A
指向圆心的力
3.作用效果:
一、向心力(centripetal force)
2.方向:
1.定义:
与速度垂直,始终指向圆心
只改变速度的方向.
不改变速度的大小,
4.计算式:
第2节 向心力
mg
N
O
T
mg
N
T
mg
N
T
mg
T
F合
mg
T
体验与猜测:
向心力大小的影响因素
实验方法
1.F与m的关系:
保持r、ω一定
2.F与r的关系:
保持m、ω一定
3.F与ω的关系:
保持r、m一定
结论: F∝m
结论: F∝r
结论: F∝ω2
F向与
ω有关
m、
r 、
控制变量法
F向=kmω2r
实验探究:
匀速转动手柄,可使塔轮、长槽和短槽匀速转动,槽内的小球也就随之做匀速圆周运动。挡板对小球的作用力提供了小球做匀速圆周运动的向心力。同时,小球挤压挡板的力使挡板另一端压缩测力套筒的弹簧,压缩量可从标尺上读出,该读数即显示了向心力的大小。
向心力演示器的结构及原理
向心力大小的影响因素
实验探究:
4π2
T2
m
r
F向=mω2r
5.变式:
指向圆心的力
3.作用效果:
一、向心力(centripetal force)
2.方向:
1.定义:
与速度垂直,始终指向圆心
只改变速度的方向.
不改变速度的大小.
4.计算式:
第2节 向心力
F向=
v2
r
m
=
mωv
=
v=ωr
注意:向心力不是一种新的力,它是一种效果力。
2π
T
ω=
地球为什么围着太阳旋转
探究向心力的来源:
F引=F向
F引
=mω2r
O
r
ω
m
探究向心力的来源:
小球在光滑玻璃漏斗中某一平面内做匀速圆周运动
重力和支持力的合力充当F向
竖直方向:
水平方向:
θ
θ
mg
N
Ncosθ=mg
Nsinθ=mω2r
F合=F向
mgtanθ
mg
N
F合
=mω2r
mgtanθ
=mω2r
gtanθ=ω2r
ω=
【典例2】(多选)如图所示,一个内壁光滑的圆锥形筒的轴线垂直于水平面,圆锥形筒固定不动,有两个质量相等的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则下列说法正确的是( )
A. 线速度A球大于B球
B. 角速度A球小于B球
C. 周期A球小于B球
D. 对筒壁的压力A球大于B球
mg
NA
mg
NB
A
B
AB
θ
mgtanθ=
=mω2r
v2
r
m
=m
4π2
T2
r
V=
ω=
T=
【变式2】(多选)如图所示,一个内壁光滑的圆锥形筒的轴线垂直于水平面,圆锥形筒固定不动,有两个小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,其中mA>mB , 则下列说法正确的是( )
A. 线速度A球大于B球
B. 角速度A球小于B球
C. 周期A球小于B球
D. 对筒壁的压力A球大于B球
mg
NA
mg
NB
A
B
ABD
θ
mgtanθ=
=mω2r
v2
r
m
=m
4π2
T2
r
V=
ω=
T=
【典例3】一根长为L=2.5 m的轻绳两端分别固定在一根竖直棒上的A、B两点,一个质量为m=0.6 kg的光滑小圆环套在绳子上,当竖直棒以一定的角速度转动时,圆环以B为圆心在水平面上做匀速圆周运动,(θ=37°,g=10 m/s2)则此时轻绳上的张力T和竖直棒转动的角速度ω各为多大( )
A.T=10N
B.T=7.5N
C.ω=3
D.ω=3
mg
T
T
mg=
Tsin370
得T=
10N
T+
Tcos370
=mω2r
r+
r
cos370
=L
得ω=
AC
3
【典例4】两根长度不同的细线下面分别悬挂两个相同小球,细线上端固定在同一点,若两个小球以相同的角速度绕共同的竖直轴在水平面内做匀速圆周运动,则两个摆球在运动过程中,相对位置关系示意图正确的是( )
B
mgtanθ=
mω2r
mg
T
θ
=mω2Lsinθ
θ
L
ω=
二、向心加速度
1.定义:
2.大小:
向心力产生的加速度,
3.方向:
a向=
F向
m
=
v2
r
=
ω2r
=
4π2
T2
r
方向总指向圆心
4.物理意义:
描述线速度方向变化的快慢。
一、向心力:
F向=
v2
r
m
=
mω2r
=
4π2
T2
m
r
=mωv
=ωv
第2节 向心力
【典例5】如图所示,一球体绕轴O1O2以角速度ω旋转,A、B为球体上两点。下列说法中正确的是( )
A. A、B两点具有相同的角速度
B. A、B两点具有相同的线速度
C. A、B两点具有相同的向心加速度
D. A、B两点的向心加速度方向都指向球心
A
三、匀速圆周运动
3.a向大小不变,
2.合力全部提供F向,
1.速度方向时刻改变,
是变速曲线.
F向大小不变,方向在变
方向时刻改变,
不是匀变速曲线运动
那变速圆周?
二、向心加速度
第2节 向心力
一、向心力
mg
T
mg
T
问题与思考:
一小球用绳栓住在竖直面内做部分圆周,
试分析小球的受力特点?
合力不再始终指向圆心
1.合力一般不等于向心力
四、变速圆周运动
2.合力中指向圆心的部分提供F向:
产生的a叫向心加速度,
3.合力中跟圆相切的部分提供切向力:
改变v的方向。
改变v的大小。
T
mg
T
mg
三、匀速圆周运动
二、向心加速度
第2节 向心力
一、向心力
产生的a叫切向加速度,
θ
T-mgcosθ=F向
=m
v2
r
mgsinθ=F切
=ma切
T-mgcosθ=ma向
【典例6】如图所示,一质量为m的木块从光滑的半球形的碗边开始下滑,在木块下滑过程中( )
A.它的加速度方向指向球心
B.它所受合力就是向心力
C.它所受向心力不断增大
D.它对碗的压力不断减小
C
mg
N
N
mg
【典例7】如图所示,汽车减速经过水平弯路
(可看做圆形轨道的一部分),关于汽车向心力
及合外力的分析正确的是( )
A.汽车拐弯时向心力由汽车方向盘来提供
B.汽车拐弯时向心力由地面来提供,与线速度方向相反
C.汽车拐弯时所受合外力指向圆心方向
D.汽车拐弯时所受合外力可能指向如图虚线方向
D
五、一般曲线运动
微元为半径在时刻改变的变速圆周运动
四、变速圆周运动
三、匀速圆周运动
二、向心加速度
第2节 向心力
一、向心力
1.处理方法:
2.曲率半径:
r2
r1
每个位置内切圆的半径
【典例8】一般的曲线运动可以分成很多小段,每小段都可以看成圆周运动的一部分,即把整条曲线用一系列不同半径的小圆弧来代替。如图(a)所示,曲线上的A点的曲率圆定义为:通过A点和曲线上紧邻A点两侧的两点作一圆,在极限情况下,这个圆就叫做A点的曲率圆,其半径ρ叫做A点的曲率半径。现将一物体沿与水平面成α角的方向以速度v0抛出,如图(b)所示。则在其轨迹最高点处的曲率半径是( )
A.v02/g
B.v02sin2α/g
C.v02cos2α/g
D.v02cos2α/gsinα
C
1.(对向心加速度的理解)下列关于向心加速度的说法正确的是( )
A.向心加速度越大,物体速率变化越快
B.向心加速度越大,物体转动得越快
C.向心加速度方向始终与速度方向垂直
D.在匀速圆周运动中,向心加速度是恒定的
C
课堂练习
2.((多选)一小球被细绳拴着在水平面内做半径为R的匀速圆周运动,向心加速度为an,那么( )
ABD
课堂练习
3.(多选)如图所示的皮带传动装置,主动轮的半径与从动轮的半径之比R1∶R2=2∶1,A、B分别是两轮边缘上的点,假定皮带不打滑,则下列说法正确的是( )
A.A、B两点的线速度之比为vA∶vB=1∶2
B.A、B两点的线速度之比为vA∶vB=1∶1
C.A 、B两点的加速度之比为aA∶aB=1∶2
D.A、B两点的加速度之比为aA∶aB=2∶1
BC
课堂练习
4.如图所示,定滑轮的半径r=2 cm。绕在滑轮上的细线悬挂着一个重物,由静止开始释放,测得重物以加速度a=2 m/s2向下做匀加速运动。在重物由静止下落1 m的瞬间,滑轮边缘上P点向心加速度多大?
答案 200 m/s2
课堂练习
