平方差公式

课件15张PPT。15.2.1平方差公式动手实践，合作探究
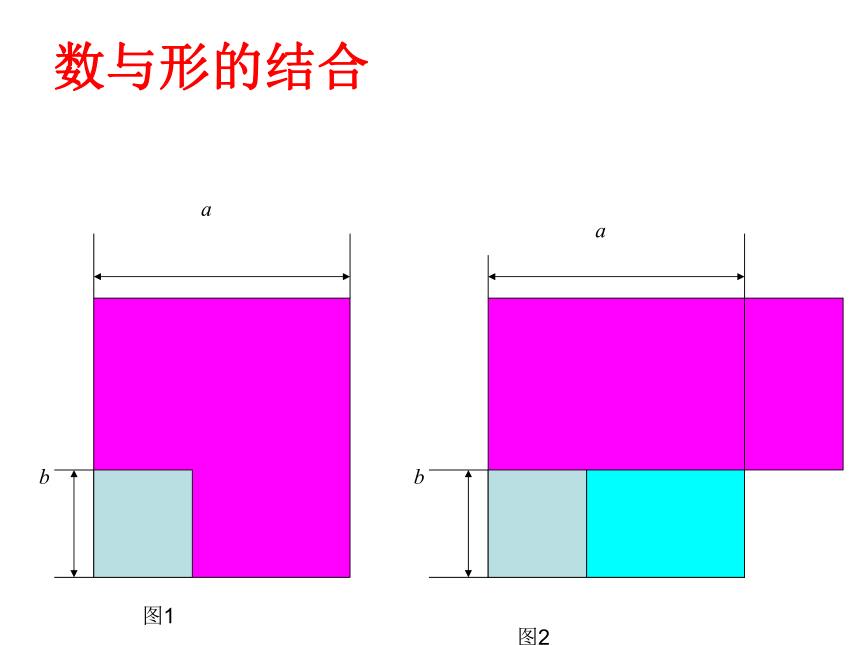
1：请你先在一张大正方形（边长为a）纸片的一角剪去一个小正方形（边长为b） ，再请你动手将剩余部分通过剪一剪、拼一拼，拼成一个长方形。2：你能用不同的方法求出剩余部分的面积吗？
3：你从中发现了什么规律？
合作交流、探索新知
计算下列多项式的积,
（1） (x+1)(x-1)=___________;
（2）(m+2)(m-2)=__________;
（3）(2x+1)(2x-1)=_________.x2-1m2- 44x2-1问题1：你能发现什么规律?
合作交流、探索新知问题2：你还能再举几个这样的算式例子 吗？问题3：说一说：为什么结果只剩下两项了呢？问题4：你能否用字母来表示呢？归纳新知：(a+b)(a-b) = .a2-b2即两个数的和与这两个数的差的积,等于这两个数的平方差.这个公式叫做(乘法的)平方差公式.议一议：平方差公式的左边、右边各有什么结构特点？验证公式:数与形的结合1、参照平方差公式填空。(1) (t+s)(t-s)=____
(2) (1+n)(1-n)=_____
(3) (10+5)(10-5)=______应用新知，尝试练习2、例1 运用平方差公式计算:
(3x+2) (3x-2);
(2) 102×98
3、辨一辨：判断下列式子是否能用平方差公式。 能不能能能不能(a+b)(a-b)=a2-b2可以运用公式的是两个二项式相乘，并且这两个二项式中有一项相同，另一项互为相反数．下面各式的计算对不对?如果不对,应当怎样改正?
(x+2)(x-2) = x2-2 ;

(2) (-3a-2) (3a-2) = 9a2 -4 .4、火眼金睛：5、学以致用： 计算下列各式
（1）(b+2a)(2a-b)
（2）(-x+2y)(-x-2y)

(3) (y+2)(y-2)-(y-1)(y+5)

(4) 51× 49 6、做题后反思
在学习时应注意观察平方差公式的特征：（4）对于形如两数和与这两数差相乘，就可以运用上述公式来计算．（3）公式中的a和b可以是具体数，也可以是单项式或多项式.（2）右边是乘式中两项的平方差
（1）左边是两个二项式相乘，并且这两个二项式中有一项相同，另一项互为相反数．(a+b)(a-b)=a2-b2
3.通过这节课的学习你体会到哪些数学思想方法？分享收获1.这节课你学到了什么知识？
2.通过这节课的学习你学会了什么？
适度拓展
1.计算 20082-2007×2009;
2.请你利用平方差公式求出(2+1)(22+1)(24+1)(28+1)(216+1)的值. 作 业必做题:作业本选做作业：《课时冲浪》P88—P89
课后作业：预习《完全平方公式》