平方差公式
图片预览






文档简介
课件24张PPT。15.2.1平方差公式 “ 解放前有一个狡猾的地主,他把一块长为x米的正方形的土地租给刘伯伯种植,有一天,地主对刘伯伯:“ 我把这块地的一边减少5米,另一边增加5米,继续租给你,你也没有吃亏,你看如何?” 刘伯伯一听觉得没有吃亏,就答应了。”一本陈旧的家书中的小故事聪明的同学们,你认为吃亏了吗?想一想 (x+1)(x-1) =
(m+2)(m-2) =
(2x+1)(2x-1) =
(x+5y)(x-5y) =x2 - 1m2 - 44x2 -1(a+b)(a-b)观察上述算式,你发现什么规律?运算出结果后,你又发现什么规律?x2 –25y21、计算 某些特殊的多项式相乘,可以写成公式的形式,当遇到相同形式的多项式相乘时,就可以直接用公式写出结果 = a2 - b2(a+b)(a-b)=a2-b2
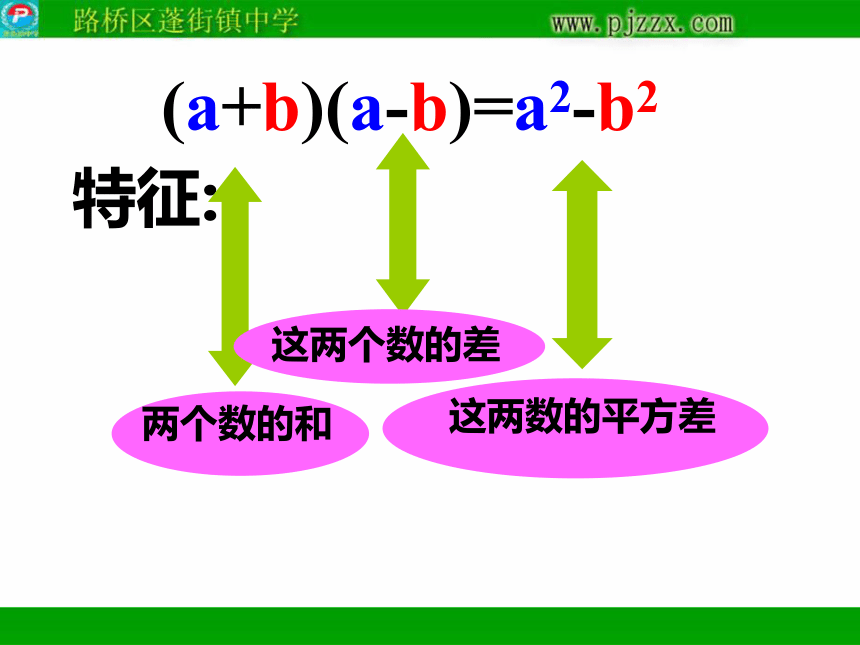
特征:(a+b)(a-b)=a2-b2
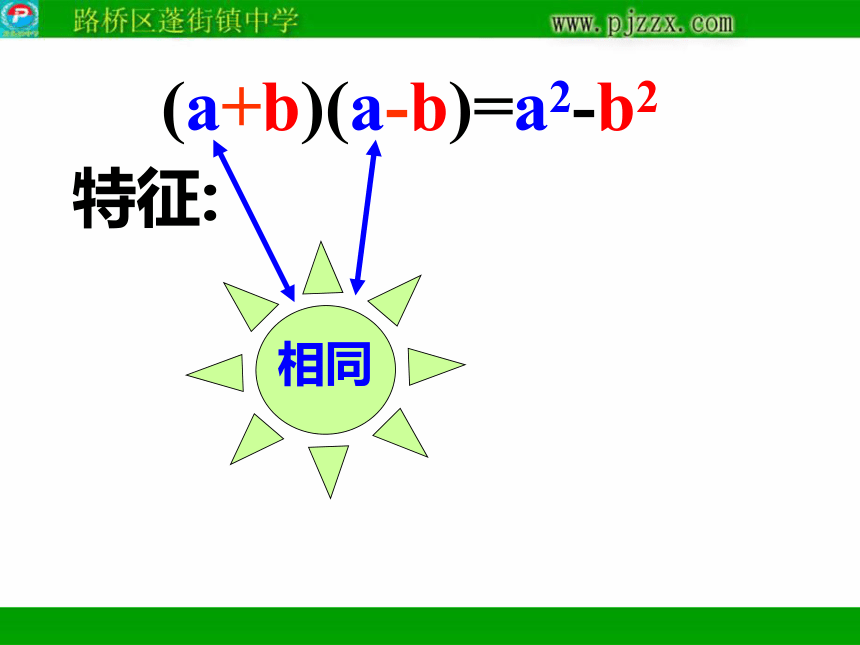
特征:(a+b)(a-b)=a2-b2
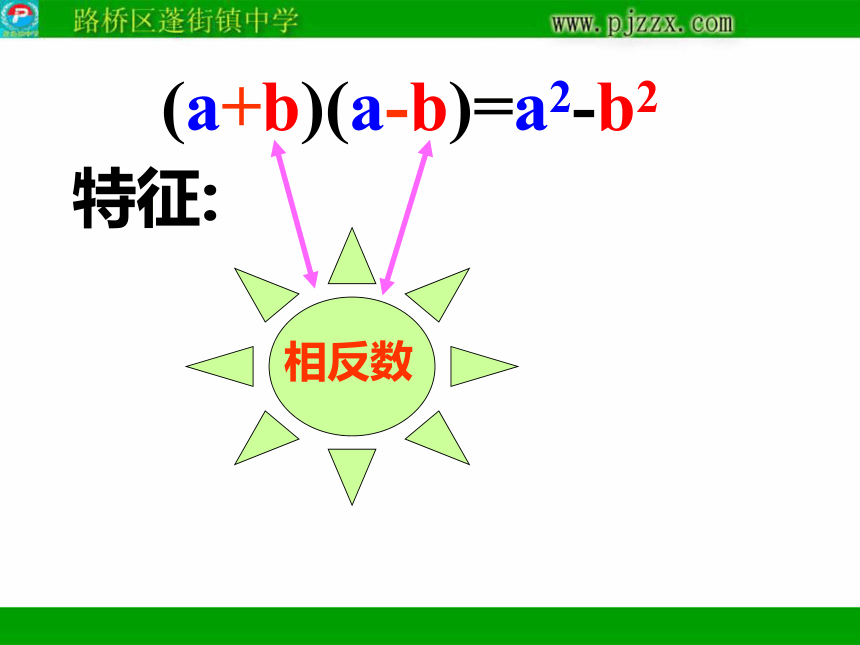
特征:(a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
特征:(a+b)(a-b) = a2-b2
平方差公式 左边
两个数的和乘以这两个数
的差 右边
这两数的平方差。 。即两个二项式中有
两项相同,另两项是互为
相反数。即相同项的平方
减去互为相反数
的项的平方。请注意:
公式中的a,b既可代表单项式,还可代表具体的数或多项式。(1+2x)(1-2x)= 12-(2x)2注意加上括号!简捷美(3m+2n)(3m-2n)变式一 ( -3m+2n)(-3m-2n)变式二 ( -3m+2n)(3m-2n)变式三 (3m+2n)(-3m+2n)变式四 (3m+2n)(-3m-2n)变式五 (-3m-2n)(3m+2n)变式六 (-2n+3m)(3m+2n)= (-3m)2-(2n)2变一变,你还能做吗? 平方差公式应用的条件两个二项式相乘其中一项相同,另一项互为相反数= (2n)2-(3m)2= (3m)2-(2n)2babbaa-ba-b 讨论:左图中黄色部分的面积S=a2 - b2S=( a+b)( a-b ) ( a+b)( a-b ) = a2 - b2b平方差公式的几何意义bab(a+b)(a-b)=a2-b2感受思想 体验快乐 例1 计算
(1) (3x+2)(3x-2) (2) (b+2a)(2a-b)
(3)(-x+2y)(-x-2y)平方差公式 (a+b)(a-b)=a2-b2运用平方差公式的计算方法:(3)套公式:a、b为整体,合理添加括号(2)比形式:适当交换项的位置,将式子整理成标
准形式,即相同项在前,互为相反数项在后。(1)抓特征:两个二项式相乘其中一项相同,
另一项互为相反数。1.2.题组一、基础练习(写出必要过程) 例2 计算:(2) (y+2)(y-2)-(y-1)(y+5);小拓展(3)20082-2009×2007题组二、深化练习(2)利用平方差公式计算: (1)(x-1)(x+1)(x2+1)(x4+1)(x8+1)(x16+1) (x32+1)(2)、运用平方差公式简便计算:
992 - 1(3)、已知 x2-y2=8 , x+y=-4 ,求x-y的值。(1)、例3、提高与应用 “ 解放前有一个狡猾的地主,他把一块长为x米的正方形的土地租给刘伯伯种植,有一天,地主对刘伯伯说:“ 我把这块地的一边减少5米,另一边增加5米,继续租给你,你也没有吃亏,你看如何?”刘伯伯一听觉得没有吃亏,就答应了。”聪明的同学们,你认为吃亏了吗?一本陈旧的家书中的小故事题组三:终级挑战(2)(2+1)(22+1)(24+1)(28+1)+1(1) (m+n+p)(m+n-p)(3)这节课你学到了什么?一个公式:(a+b)(a-b)=a2-b2(1)简化某些多项式的乘法运算
(2)提供有理数乘法的速算方法两种作用(1)公式中的ab表示数、单项式、多项式三个注意数学思想方法(2)要符合公式特征的才能用平方差公式(3)有些式子表面上不能应用公式,但通
过适当变形实质上能应用公式再见作业提示:作业本(1)
(m+2)(m-2) =
(2x+1)(2x-1) =
(x+5y)(x-5y) =x2 - 1m2 - 44x2 -1(a+b)(a-b)观察上述算式,你发现什么规律?运算出结果后,你又发现什么规律?x2 –25y21、计算 某些特殊的多项式相乘,可以写成公式的形式,当遇到相同形式的多项式相乘时,就可以直接用公式写出结果 = a2 - b2(a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
特征:(a+b)(a-b) = a2-b2
平方差公式 左边
两个数的和乘以这两个数
的差 右边
这两数的平方差。 。即两个二项式中有
两项相同,另两项是互为
相反数。即相同项的平方
减去互为相反数
的项的平方。请注意:
公式中的a,b既可代表单项式,还可代表具体的数或多项式。(1+2x)(1-2x)= 12-(2x)2注意加上括号!简捷美(3m+2n)(3m-2n)变式一 ( -3m+2n)(-3m-2n)变式二 ( -3m+2n)(3m-2n)变式三 (3m+2n)(-3m+2n)变式四 (3m+2n)(-3m-2n)变式五 (-3m-2n)(3m+2n)变式六 (-2n+3m)(3m+2n)= (-3m)2-(2n)2变一变,你还能做吗? 平方差公式应用的条件两个二项式相乘其中一项相同,另一项互为相反数= (2n)2-(3m)2= (3m)2-(2n)2babbaa-ba-b 讨论:左图中黄色部分的面积S=a2 - b2S=( a+b)( a-b ) ( a+b)( a-b ) = a2 - b2b平方差公式的几何意义bab(a+b)(a-b)=a2-b2感受思想 体验快乐 例1 计算
(1) (3x+2)(3x-2) (2) (b+2a)(2a-b)
(3)(-x+2y)(-x-2y)平方差公式 (a+b)(a-b)=a2-b2运用平方差公式的计算方法:(3)套公式:a、b为整体,合理添加括号(2)比形式:适当交换项的位置,将式子整理成标
准形式,即相同项在前,互为相反数项在后。(1)抓特征:两个二项式相乘其中一项相同,
另一项互为相反数。1.2.题组一、基础练习(写出必要过程) 例2 计算:(2) (y+2)(y-2)-(y-1)(y+5);小拓展(3)20082-2009×2007题组二、深化练习(2)利用平方差公式计算: (1)(x-1)(x+1)(x2+1)(x4+1)(x8+1)(x16+1) (x32+1)(2)、运用平方差公式简便计算:
992 - 1(3)、已知 x2-y2=8 , x+y=-4 ,求x-y的值。(1)、例3、提高与应用 “ 解放前有一个狡猾的地主,他把一块长为x米的正方形的土地租给刘伯伯种植,有一天,地主对刘伯伯说:“ 我把这块地的一边减少5米,另一边增加5米,继续租给你,你也没有吃亏,你看如何?”刘伯伯一听觉得没有吃亏,就答应了。”聪明的同学们,你认为吃亏了吗?一本陈旧的家书中的小故事题组三:终级挑战(2)(2+1)(22+1)(24+1)(28+1)+1(1) (m+n+p)(m+n-p)(3)这节课你学到了什么?一个公式:(a+b)(a-b)=a2-b2(1)简化某些多项式的乘法运算
(2)提供有理数乘法的速算方法两种作用(1)公式中的ab表示数、单项式、多项式三个注意数学思想方法(2)要符合公式特征的才能用平方差公式(3)有些式子表面上不能应用公式,但通
过适当变形实质上能应用公式再见作业提示:作业本(1)
