三角形的中位线1
图片预览


文档简介
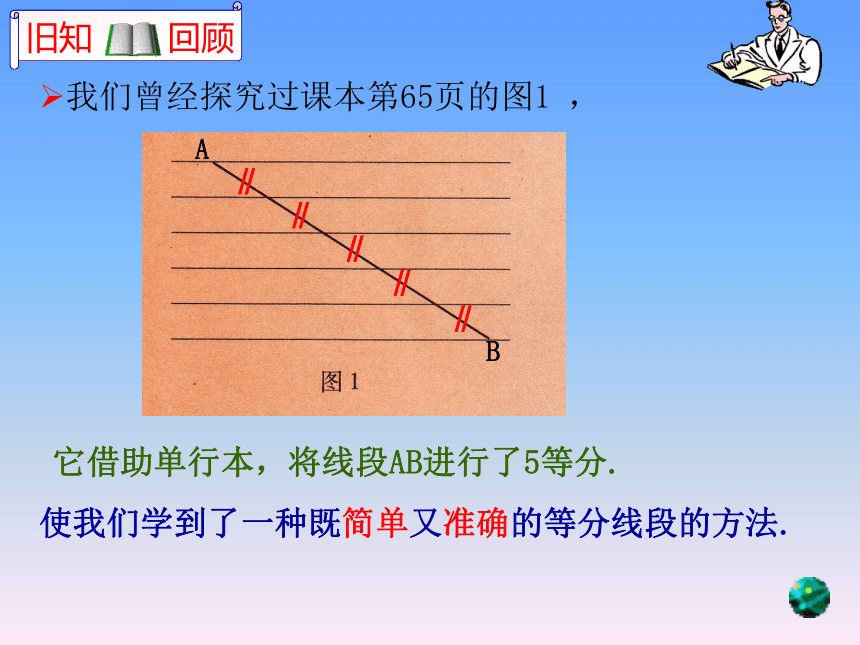
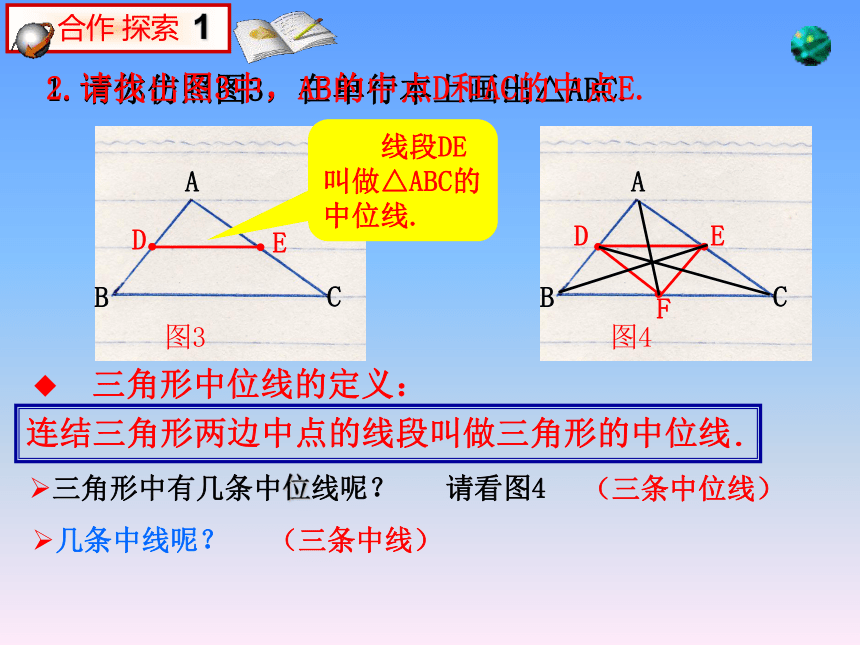
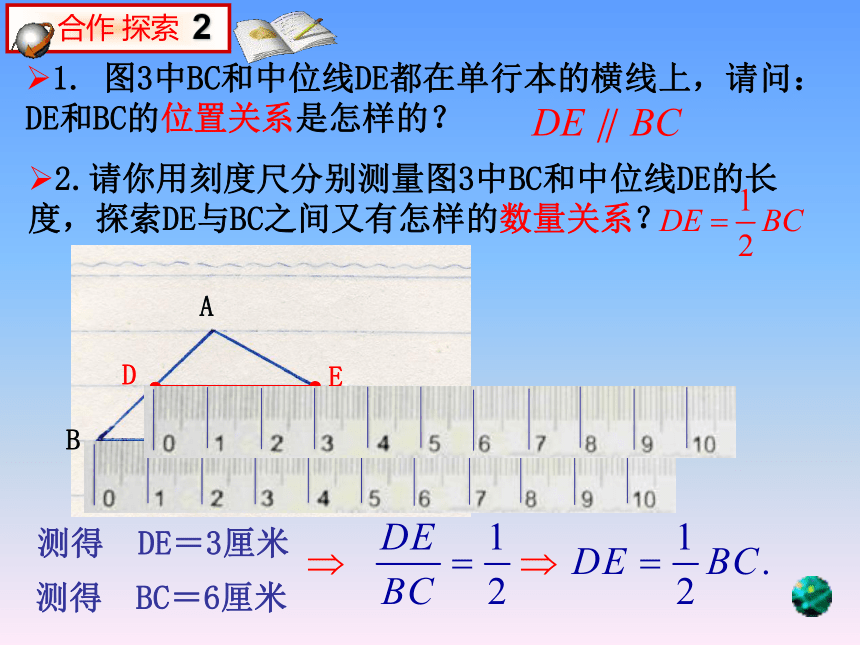
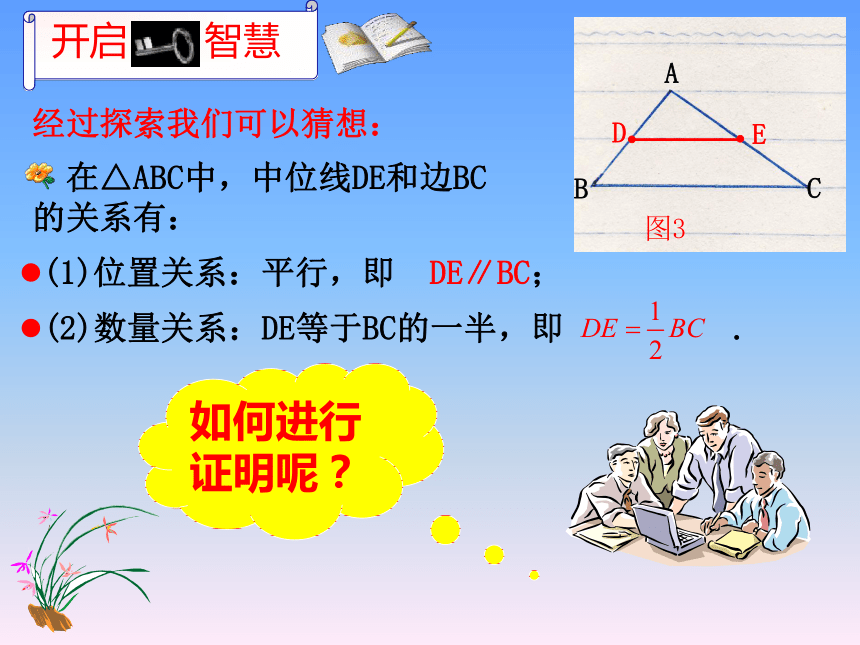
课件15张PPT。它借助单行本,将线段AB进行了5等分.我们曾经探究过课本第65页的图1 ,使我们学到了一种既简单又准确的等分线段的方法.∥∥∥∥∥AB1.请你仿照图3,在单行本上画出△ABC.DE 线段DE叫做△ABC的中位线.连结三角形两边中点的线段叫做三角形的中位线. 三角形中位线的定义:三角形中有几条中位线呢?几条中线呢?DEF(三条中位线)(三条中线)2.请找出图3中,AB的中点D和AC的中点E.请看图42.请你用刻度尺分别测量图3中BC和中位线DE的长度,探索DE与BC之间又有怎样的数量关系?1. 图3中BC和中位线DE都在单行本的横线上,请问:DE和BC的位置关系是怎样的?测得 BC=6厘米测得 DE=3厘米经过探索我们可以猜想: 在△ABC中,中位线DE和边BC的关系有:(1)位置关系:平行,即 DE∥BC;如何进行证明呢?证明 :如图3,在△ABC中,点D、E又∵ ∠A=∠A,
∴ △ADE∽△ABC.
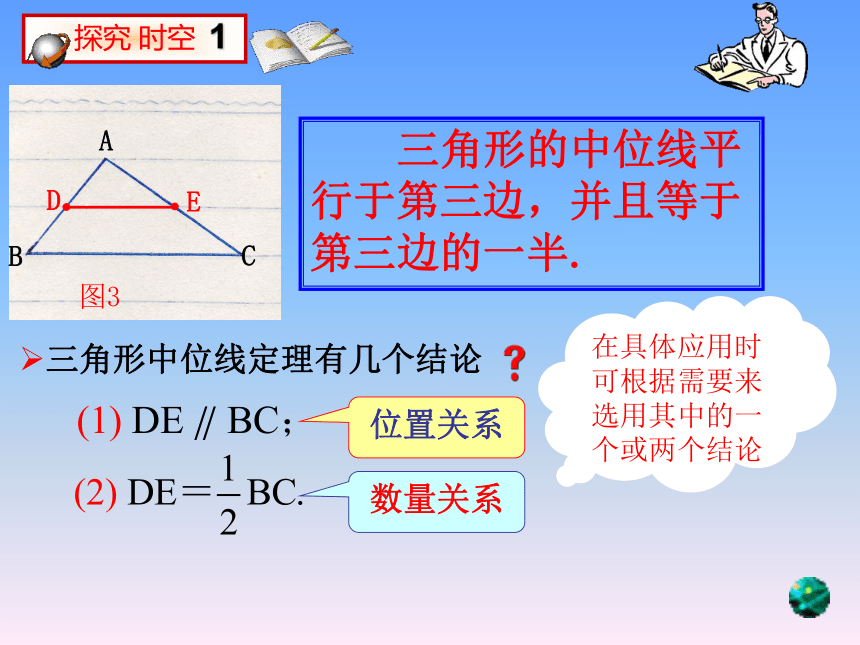
∴ ∠ADE=∠ABC,∴三角形的中位线平行于第三边,并且等于第三边的一半. 三角形中位线定理:分别是AB与AC的中点,(如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似)(相似三角形的对应角相等,对应边成比例)如图3,在△ABC中,点D、E分别是AB与AC的中点,条件△ADE ∽ △ABC∵ 在△ABC中,点D、E分别是AB与AC的中点∴又∵∠A=∠A分析: 请你将书写的证明过程与同桌进行交流.请你再和老师写的比较一下 三角形中位线定理有几个结论在具体应用时可根据需要来选用其中的一个或两个结论 三角形的中位线平行于第三边,并且等于第三边的一半.位置关系数量关系三角形的中位线平行于第三边,并且等于第三边的一半.2.如图,在△ABC中,∠C=90°,AC=3,BC=4.若D、E分别是AC、BC的中点,则DE=_______.3.如图,在△ABC中,D、E、F分别为边AB、AC、BC的中点,若△ABC的周长为18cm,则△DEF的周长为_______. 1.如图,在△ABC中,D、E分别是AB、AC的中点,∠ABC=60°,BC=10,则∠ADE=__, DE=____. 求证三角形的一条中位线与第三边上的中线互相平分.对于文字题,首先应根据题意,画出图形,写出已知,求证.∴ DE∥AC(三角形的中位线平行于第三边)同理 EF∥AB.∴ 四边形ADEF是平行四边形.∴ AE、DF互相平分.(平行四边形的对角线互相平分)两组对边分别平行的四边形是平行四边形我的地盘我作主!∵ D、E分别为BC、AC的中点,∴ BD=DC,CE=EA.又∵ 点D是BC的中点,1.【08太原】如图,在△ABC中,D、E分别是AB、AC边的中点,已知BC=10,则DE的长为( )A.3; B.4; C.5 ; D.6.C2.【07温州】如图,若D,E分别是AB,AC中点,现测得DE的长为20米,则池塘的宽BC是__米. 3.【08东莞】如图1,在ΔABC中,M、N分别是AB、AC的中点,且∠A+∠B=120°,则∠ANM=___° 6040BADCD′E直接旋转(A′)点拨:在证明四边形DBCD′是平行四边形时,要注意证明点D、E、D′在同一条直线上.F点拨:方法一,延长DE至F,使EF=DE;
方法二,过点C作CF∥AB交DE的延长线于点F.截长补短三角形的中位线平行于第三边,并且等于第三边的一半.请同学们课后继续进行探究,完成证明过程.本节学习了三角形中位线概念及中位线定理;感受了三角形中位线定理的应用思想,以及体会了数学推理的应用价值.三角形中位线定理,是三角形的一个重要性质定理,这个定理有一个特点:在同一个题设下,有两个结论,一个结论是表明位置关系的,另一个结论是表明数量关系(倍分关系)的.在应用三角形中位线定理时,不一定同时需要两个结论,有时需要平行关系,有时需要数量关系,可以根据具体情况,按需选用.1.已知△ABC中,D、E、F分别是△ABC的三边中点,且DE︰EF︰FD=3︰5︰6,若△ABC的周长为112cm,求DE、EF、FD的长.
2.课本P70页 习题24.4 第3题、第4题. 课堂作业:1.课本P70页 习题24.4 第1题.课外作业:2.课本P70页 练习 第3题.
∴ △ADE∽△ABC.
∴ ∠ADE=∠ABC,∴三角形的中位线平行于第三边,并且等于第三边的一半. 三角形中位线定理:分别是AB与AC的中点,(如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似)(相似三角形的对应角相等,对应边成比例)如图3,在△ABC中,点D、E分别是AB与AC的中点,条件△ADE ∽ △ABC∵ 在△ABC中,点D、E分别是AB与AC的中点∴又∵∠A=∠A分析: 请你将书写的证明过程与同桌进行交流.请你再和老师写的比较一下 三角形中位线定理有几个结论在具体应用时可根据需要来选用其中的一个或两个结论 三角形的中位线平行于第三边,并且等于第三边的一半.位置关系数量关系三角形的中位线平行于第三边,并且等于第三边的一半.2.如图,在△ABC中,∠C=90°,AC=3,BC=4.若D、E分别是AC、BC的中点,则DE=_______.3.如图,在△ABC中,D、E、F分别为边AB、AC、BC的中点,若△ABC的周长为18cm,则△DEF的周长为_______. 1.如图,在△ABC中,D、E分别是AB、AC的中点,∠ABC=60°,BC=10,则∠ADE=__, DE=____. 求证三角形的一条中位线与第三边上的中线互相平分.对于文字题,首先应根据题意,画出图形,写出已知,求证.∴ DE∥AC(三角形的中位线平行于第三边)同理 EF∥AB.∴ 四边形ADEF是平行四边形.∴ AE、DF互相平分.(平行四边形的对角线互相平分)两组对边分别平行的四边形是平行四边形我的地盘我作主!∵ D、E分别为BC、AC的中点,∴ BD=DC,CE=EA.又∵ 点D是BC的中点,1.【08太原】如图,在△ABC中,D、E分别是AB、AC边的中点,已知BC=10,则DE的长为( )A.3; B.4; C.5 ; D.6.C2.【07温州】如图,若D,E分别是AB,AC中点,现测得DE的长为20米,则池塘的宽BC是__米. 3.【08东莞】如图1,在ΔABC中,M、N分别是AB、AC的中点,且∠A+∠B=120°,则∠ANM=___° 6040BADCD′E直接旋转(A′)点拨:在证明四边形DBCD′是平行四边形时,要注意证明点D、E、D′在同一条直线上.F点拨:方法一,延长DE至F,使EF=DE;
方法二,过点C作CF∥AB交DE的延长线于点F.截长补短三角形的中位线平行于第三边,并且等于第三边的一半.请同学们课后继续进行探究,完成证明过程.本节学习了三角形中位线概念及中位线定理;感受了三角形中位线定理的应用思想,以及体会了数学推理的应用价值.三角形中位线定理,是三角形的一个重要性质定理,这个定理有一个特点:在同一个题设下,有两个结论,一个结论是表明位置关系的,另一个结论是表明数量关系(倍分关系)的.在应用三角形中位线定理时,不一定同时需要两个结论,有时需要平行关系,有时需要数量关系,可以根据具体情况,按需选用.1.已知△ABC中,D、E、F分别是△ABC的三边中点,且DE︰EF︰FD=3︰5︰6,若△ABC的周长为112cm,求DE、EF、FD的长.
2.课本P70页 习题24.4 第3题、第4题. 课堂作业:1.课本P70页 习题24.4 第1题.课外作业:2.课本P70页 练习 第3题.
