人教版八年级数学上册第十一章《三角形》期末专项复习卷(含答案)
文档属性
| 名称 | 人教版八年级数学上册第十一章《三角形》期末专项复习卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 175.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-11 00:00:00 | ||
图片预览




文档简介
八年级数学上册第十一章《三角形》期末专项复习卷
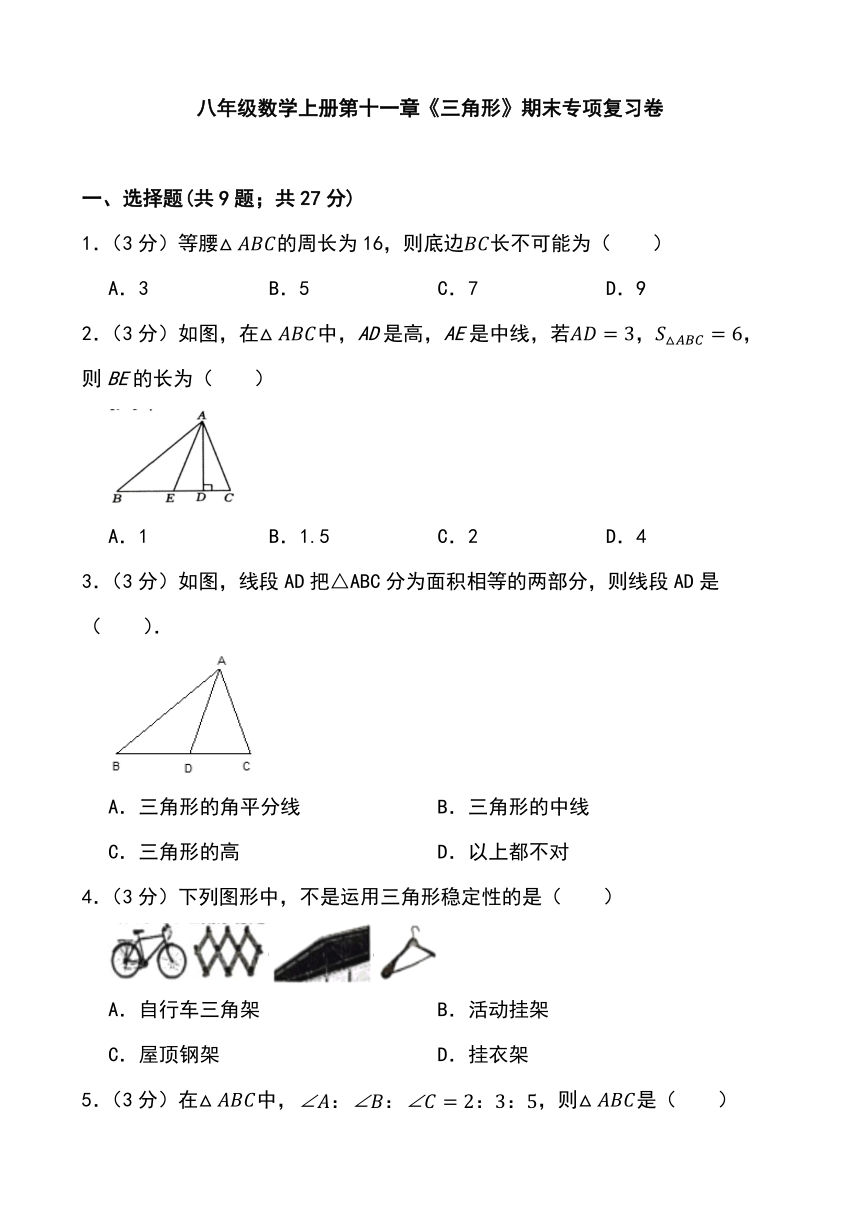
一、选择题(共9题;共27分)
1.(3分)等腰的周长为16,则底边长不可能为( )
A.3 B.5 C.7 D.9
2.(3分)如图,在中,AD是高,AE是中线,若,,则BE的长为( )
A.1 B.1.5 C.2 D.4
3.(3分)如图,线段AD把△ABC分为面积相等的两部分,则线段AD是( ).
A.三角形的角平分线 B.三角形的中线
C.三角形的高 D.以上都不对
4.(3分)下列图形中,不是运用三角形稳定性的是( )
A.自行车三角架 B.活动挂架
C.屋顶钢架 D.挂衣架
5.(3分)在中,,则是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.不能确定
6.(3分)如图,在△ABC中,∠BCA=40°,∠ABC=60°.若BF是△ABC的高,与角平分线AE相交于点O,则∠EOF的度数为( )
A.130° B.70° C.110 D.100°
7.(3分)如图,要使一个七边形木架不变形,至少要再钉上木条的根数是( )
A.1根 B.2根 C.3根 D.4根
8.(3分)若一个多边形截去一个角后,形成的新多边形的内角和是.则原来多边形的边数可能是( )
A.10或11 B.11 C.11或12 D.10或11或12
9.(3分)用同一种正多边形能铺满地面的是( )
A.正五边形 B.正六边形 C.正九边形 D.正十边形
二、填空题(共9题;共27分)
10.(3分)如图,在 中, ,将 平移5个单位长度得到 1,点P、Q分别是 、 的中点, 的最小值等于 .
11.(3分)如图, 分别是 的边 上的中点,连接 交于点G, , 的面积为6,设 的面积为 , 的面积为 ,则 .
12.(3分)如图,已知△ABC是等边三角形,点O是BC上任意一点,OE⊥AB,OF⊥AC,等边三角形的高为2,则OE+OF的值为 .
13.(3分)△ABC中,∠A是最小角,∠B是最大角,且2∠B=5∠A,若∠B的最大值m°,最小值n°,则m+n= .
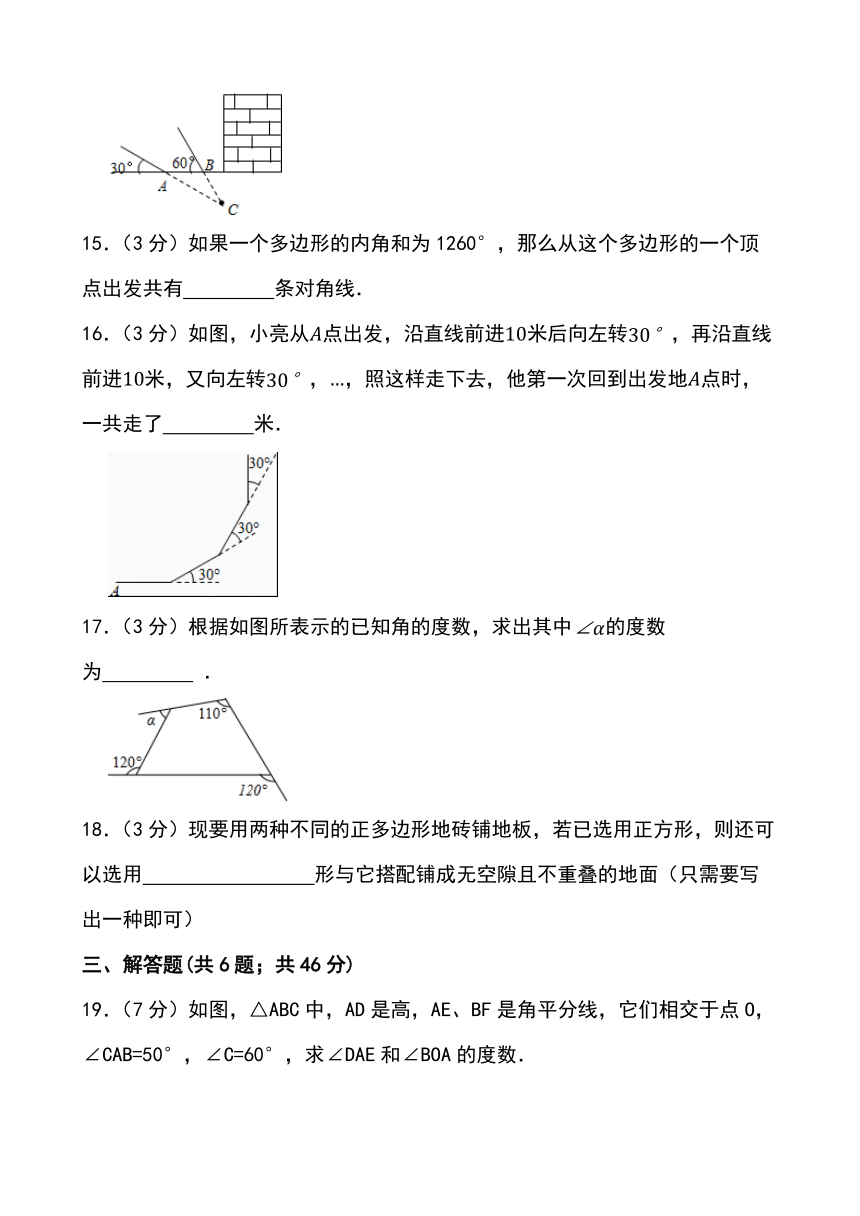
14.(3分) 年 月 日凌晨,宝岛高雄发生 级地震,得知消息后,中国派出武警部队探测队,探测队探测出某建筑物下面有生命迹象,他们在生命迹象上方建筑物的一侧地面上的 两处,用仪器探测生命迹象 ,已知探测线与地面的夹角分别是 和 (如图),则 的度数是 .
15.(3分)如果一个多边形的内角和为1260°,那么从这个多边形的一个顶点出发共有 条对角线.
16.(3分)如图,小亮从点出发,沿直线前进米后向左转,再沿直线前进米,又向左转,,照这样走下去,他第一次回到出发地点时,一共走了 米.
17.(3分)根据如图所表示的已知角的度数,求出其中的度数为 .
18.(3分)现要用两种不同的正多边形地砖铺地板,若已选用正方形,则还可以选用 形与它搭配铺成无空隙且不重叠的地面(只需要写出一种即可)
三、解答题(共6题;共46分)
19.(7分)如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠CAB=50°,∠C=60°,求∠DAE和∠BOA的度数.
20.(7分)如图,在△ABC中,AD,AE分别是BC边上的高线和中线.若△ABC的面积是24,AD长为6,BD-DE=1,求△ADE的面积.
21.(8分)如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E.
(1)(4分)若∠B=35°,∠E=25°,求∠BAC的度数;
(2)(4分)证明:∠BAC=∠B+2∠E.
22.(8分)已知:射线是的外角的平分线.
(1)(4分)如图1,延长交射线于点E,若,,求的度数;
(2)(4分)如图2,射线交于点G,若,求证:平分.
23.(8分) 在一个各内角都相等的多边形中,每一个内角都比相邻外角的倍还大,
(1)(4分)求这个多边形的边数;
(2)(4分)若将这个多边形剪去一个角,剩下多边形的内角和是多少?
24.(8分)如图,BD是△ABC的角平分线,DE⊥AB,垂足为E. △ABC的面积为70,AB=16,BC=12. 求DE的长。
答案解析部分
1.D
2.C
3.B
4.B
5.C
6.A
7.D
8.D
9.B
10.
11.2
12.2
13.175
14.
15.6
16.
17.50°
18.正三角形(答案不唯一)
19.解:∵∠CAB=50°,∠C=60°
∴∠ABC=180°﹣50°﹣60°=70°,
又∵AD是高,
∴∠ADC=90°,
∴∠DAC=180°﹣90°﹣∠C=30°,
∵AE、BF是角平分线,
∴∠CBF=∠ABF=35°,∠EAF=25°,
∴∠DAE=∠DAC﹣∠EAF=5°,
∠AFB=∠C+∠CBF=60°+35°=95°,
∴∠BOA=∠EAF+∠AFB=25°+95°=120°,
∴∠DAC=30°,∠BOA=120°.
故∠DAE=5°,∠BOA=120°.
20.解:∵AD是BC边上的高线,
∴AD⊥BC,
∴,
∴BC=8,
∵AE是BC边上的中线,
∴BE=CE==4,
又 BD-DE=1,BD+DE=4,
∴DE=1.5,
∴.
21.(1)解:∵∠B=35°,∠E=25°,
∴∠ECD=∠B+∠E=60°.
∵CE平分∠ACD,
∴∠ACE=∠ECD=60°,
∴∠BAC=∠ACE+∠E=85°;
(2)证明:∵CE平分∠ACD,
∴∠ECD=∠ACE.
∵∠BAC=∠E+∠ACE,
∴∠BAC=∠E+∠ECD,
∵∠ECD=∠B+∠E,
∴∠BAC=∠E+∠B+∠E,
∴∠BAC=∠B+2∠E.
22.(1)解:∵,,
∴,
∵射线是的外角的平分线.
∴,
∴;
(2)解:∵射线是的外角的平分线.
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴平分.
23.(1)解:设多边形的一个外角为,则与其相邻的内角等于,
由题意,得,解得.
即多边形的每个外角为.
又多边形的外角和为,
多边形的外角个数.
多边形的边数,
答:这个多边形的边数是;
(2)解:因为剪掉一个角以后,多边形的边数可能增加了条,也可能减少了条,或者不变,
当截线经过多边形的个顶点时,多边形的边数减少了条边,
内角和;
当截线经过多边形一个顶点时,多边形的边数不变,
内角和;
当截线不经过正多形的顶点时,多边形的边数增加一条边,
内角和.
答:将这个多边形剪去一个角,剩下多边形的内角和是或或.
24.解:如图,过点D作DF⊥BC于F,
∵BD是△ABC的角平分线,DE⊥AB,
∴DE=DF,
S△ABC= ×16 DE+ ×12 DF=70,
所以,14DE=70,
解得DE=5.
一、选择题(共9题;共27分)
1.(3分)等腰的周长为16,则底边长不可能为( )
A.3 B.5 C.7 D.9
2.(3分)如图,在中,AD是高,AE是中线,若,,则BE的长为( )
A.1 B.1.5 C.2 D.4
3.(3分)如图,线段AD把△ABC分为面积相等的两部分,则线段AD是( ).
A.三角形的角平分线 B.三角形的中线
C.三角形的高 D.以上都不对
4.(3分)下列图形中,不是运用三角形稳定性的是( )
A.自行车三角架 B.活动挂架
C.屋顶钢架 D.挂衣架
5.(3分)在中,,则是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.不能确定
6.(3分)如图,在△ABC中,∠BCA=40°,∠ABC=60°.若BF是△ABC的高,与角平分线AE相交于点O,则∠EOF的度数为( )
A.130° B.70° C.110 D.100°
7.(3分)如图,要使一个七边形木架不变形,至少要再钉上木条的根数是( )
A.1根 B.2根 C.3根 D.4根
8.(3分)若一个多边形截去一个角后,形成的新多边形的内角和是.则原来多边形的边数可能是( )
A.10或11 B.11 C.11或12 D.10或11或12
9.(3分)用同一种正多边形能铺满地面的是( )
A.正五边形 B.正六边形 C.正九边形 D.正十边形
二、填空题(共9题;共27分)
10.(3分)如图,在 中, ,将 平移5个单位长度得到 1,点P、Q分别是 、 的中点, 的最小值等于 .
11.(3分)如图, 分别是 的边 上的中点,连接 交于点G, , 的面积为6,设 的面积为 , 的面积为 ,则 .
12.(3分)如图,已知△ABC是等边三角形,点O是BC上任意一点,OE⊥AB,OF⊥AC,等边三角形的高为2,则OE+OF的值为 .
13.(3分)△ABC中,∠A是最小角,∠B是最大角,且2∠B=5∠A,若∠B的最大值m°,最小值n°,则m+n= .
14.(3分) 年 月 日凌晨,宝岛高雄发生 级地震,得知消息后,中国派出武警部队探测队,探测队探测出某建筑物下面有生命迹象,他们在生命迹象上方建筑物的一侧地面上的 两处,用仪器探测生命迹象 ,已知探测线与地面的夹角分别是 和 (如图),则 的度数是 .
15.(3分)如果一个多边形的内角和为1260°,那么从这个多边形的一个顶点出发共有 条对角线.
16.(3分)如图,小亮从点出发,沿直线前进米后向左转,再沿直线前进米,又向左转,,照这样走下去,他第一次回到出发地点时,一共走了 米.
17.(3分)根据如图所表示的已知角的度数,求出其中的度数为 .
18.(3分)现要用两种不同的正多边形地砖铺地板,若已选用正方形,则还可以选用 形与它搭配铺成无空隙且不重叠的地面(只需要写出一种即可)
三、解答题(共6题;共46分)
19.(7分)如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠CAB=50°,∠C=60°,求∠DAE和∠BOA的度数.
20.(7分)如图,在△ABC中,AD,AE分别是BC边上的高线和中线.若△ABC的面积是24,AD长为6,BD-DE=1,求△ADE的面积.
21.(8分)如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E.
(1)(4分)若∠B=35°,∠E=25°,求∠BAC的度数;
(2)(4分)证明:∠BAC=∠B+2∠E.
22.(8分)已知:射线是的外角的平分线.
(1)(4分)如图1,延长交射线于点E,若,,求的度数;
(2)(4分)如图2,射线交于点G,若,求证:平分.
23.(8分) 在一个各内角都相等的多边形中,每一个内角都比相邻外角的倍还大,
(1)(4分)求这个多边形的边数;
(2)(4分)若将这个多边形剪去一个角,剩下多边形的内角和是多少?
24.(8分)如图,BD是△ABC的角平分线,DE⊥AB,垂足为E. △ABC的面积为70,AB=16,BC=12. 求DE的长。
答案解析部分
1.D
2.C
3.B
4.B
5.C
6.A
7.D
8.D
9.B
10.
11.2
12.2
13.175
14.
15.6
16.
17.50°
18.正三角形(答案不唯一)
19.解:∵∠CAB=50°,∠C=60°
∴∠ABC=180°﹣50°﹣60°=70°,
又∵AD是高,
∴∠ADC=90°,
∴∠DAC=180°﹣90°﹣∠C=30°,
∵AE、BF是角平分线,
∴∠CBF=∠ABF=35°,∠EAF=25°,
∴∠DAE=∠DAC﹣∠EAF=5°,
∠AFB=∠C+∠CBF=60°+35°=95°,
∴∠BOA=∠EAF+∠AFB=25°+95°=120°,
∴∠DAC=30°,∠BOA=120°.
故∠DAE=5°,∠BOA=120°.
20.解:∵AD是BC边上的高线,
∴AD⊥BC,
∴,
∴BC=8,
∵AE是BC边上的中线,
∴BE=CE==4,
又 BD-DE=1,BD+DE=4,
∴DE=1.5,
∴.
21.(1)解:∵∠B=35°,∠E=25°,
∴∠ECD=∠B+∠E=60°.
∵CE平分∠ACD,
∴∠ACE=∠ECD=60°,
∴∠BAC=∠ACE+∠E=85°;
(2)证明:∵CE平分∠ACD,
∴∠ECD=∠ACE.
∵∠BAC=∠E+∠ACE,
∴∠BAC=∠E+∠ECD,
∵∠ECD=∠B+∠E,
∴∠BAC=∠E+∠B+∠E,
∴∠BAC=∠B+2∠E.
22.(1)解:∵,,
∴,
∵射线是的外角的平分线.
∴,
∴;
(2)解:∵射线是的外角的平分线.
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴平分.
23.(1)解:设多边形的一个外角为,则与其相邻的内角等于,
由题意,得,解得.
即多边形的每个外角为.
又多边形的外角和为,
多边形的外角个数.
多边形的边数,
答:这个多边形的边数是;
(2)解:因为剪掉一个角以后,多边形的边数可能增加了条,也可能减少了条,或者不变,
当截线经过多边形的个顶点时,多边形的边数减少了条边,
内角和;
当截线经过多边形一个顶点时,多边形的边数不变,
内角和;
当截线不经过正多形的顶点时,多边形的边数增加一条边,
内角和.
答:将这个多边形剪去一个角,剩下多边形的内角和是或或.
24.解:如图,过点D作DF⊥BC于F,
∵BD是△ABC的角平分线,DE⊥AB,
∴DE=DF,
S△ABC= ×16 DE+ ×12 DF=70,
所以,14DE=70,
解得DE=5.
