5.1.2 弧度制-2023-2024学年高二数学 课件(共18张PPT)
文档属性
| 名称 | 5.1.2 弧度制-2023-2024学年高二数学 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-11 06:59:00 | ||
图片预览






文档简介
(共18张PPT)
5.1 任意角与弧度制
5.1.2 弧度制
1. 通过类比不同度量制,了解弧度制的概念;
2. 掌握弧度与角度的互化;
3. 掌握并能运用弧度制下的弧长公式和扇形面积公式;
问题 1:结合生活中常见的汽车仪表盘,说一说,图中两圈不同数字的含义?
拓展:外圈数字单位是“千米/小时” ;
内圈数字是英制,单位为“英里/小时”.
思考:参照上述事例,说一说,角的度量是否也能用不同的单位制呢?
知识点1:弧度制的概念
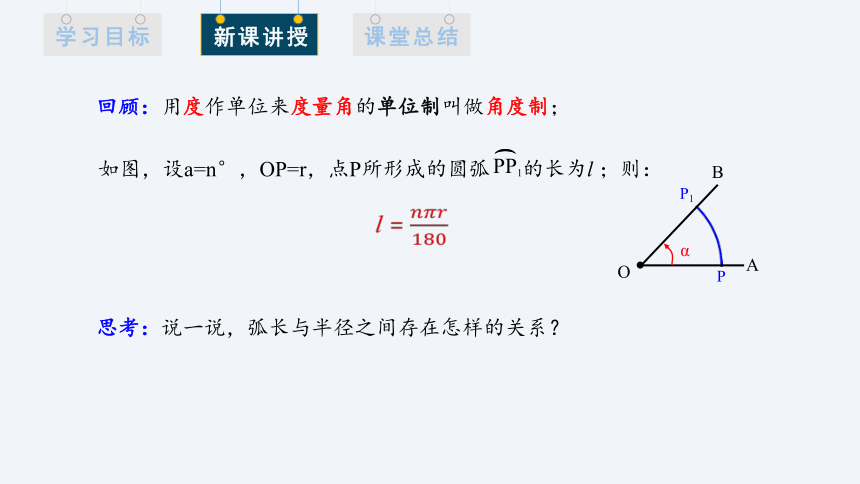
回顾:用度作单位来度量角的单位制叫做角度制;
如图,设a=n°,OP=r,点P所形成的圆弧 的长为l ;则:
PP1
O
A
B
α
P
P1
l =
思考:说一说,弧长与半径之间存在怎样的关系?
问题 2 :如图,在射线OA上任取一点Q(不同于点O),OQ=r1,在旋转过程中,点Q所形成的圆弧QQ1的长为l1. l1与r1的比值是多少?你能得出什么结论?
O
A
B
α
P
P1
Q1
Q
= n
由:l1 = ,得:
结论:圆心角α所对的弧长与半径的比值,只与α的大小有关;
即:这个比值随α的确定而唯一确定.
概念讲解
前提:圆心角α一定时,其所对的弧长与半径的比值一定,故可以用圆的弧长与半径的关系度量圆心角;
规定:长度等于半径长的圆弧所对的圆心角叫做 1 弧度的角;
弧度单位用符号rad表示,读作弧度;
用弧度作单位来度量角的单位制叫做弧度制;
例:如图,在单位圆(半径为1的圆)O中,AB的长
等于1,∠AOB就是1弧度的角.
x
y
O
A
B
1 rad
1
根据上述规定,在半径为 r 的圆中,弧长为 l 的弧所对的圆心角为 α rad,那么:
|α| = = n .
注意:
(1)类似角的正负,角的终边逆时针旋转 α 为正,顺时针旋转 α 为负;
(2)角的终边旋转超过一周后,可得弧度数大于2π或小于-2π的角;
即可用弧度表示任意大小的角;
(3)正角的弧度数是正数,负角的弧度数是负数,零角的弧度数是0.
例 2 :通过对比角度制与弧度制的区别与联系,完成下列表格.
弧度制 角度制
区别
联系
无论弧度制还是角度制,
角的大小都是一个与半径大小无关的定值
弧度制以线段长度来度量角
角度制是“以角量角”
弧度制是十进制
角度制是六十进制
1弧度是等于半径长的弧
所对的圆心角的大小
1°的角是周角的
思考:结合前面的汽车仪表盘事例,我们可以知道千米和英里之间存在一定的换算关系,那么角度制、弧度制之间也存在这样的换算关系吗?如果存在,又该如何换算呢?
知识点2:角度与弧度的换算
x
y
O
由 |α| = 可知,周角的弧度数为:α = = 2π rad;
故 360° = 2π rad, 180° = π rad.
注意:上述 180° 是对应 π rad,而不是对应 实数 π.
角度与弧度的换算公式:
180°= π rad
1°= rad ≈ 0.017 45 rad
1 rad = ()°≈ 57.30°
角度数 = 弧度数× ()°
弧度数 = 角度数×
例 3 :运用角度与弧度的换算公式,把下列角度化成弧度.
(1)22°30 ; (2)-210°(精确到0.001).
解:(1)∵ 22°30 = 22.5°,∴ 22.5°= 22.5× = 0.125 π;
(2) -210° = -210× = -1.167 π rad.
注意:
(1)角度中含有 分( )、秒( ) 时,化成弧度制之前,要先化成 度(°);
(2)负角换算成弧度后仍旧是一个负数.
例 4 :把下列弧度化成角度.
(1); (2)-.
解:(1) × ()°= 15°;
(2)- × ()°= -240°.
练一练
度 0° 30° 45° 120° 135° 150° 360°
弧度 π
1.运用换算公式,填写下列特殊角的度数与弧度数的对应表:
90°
60°
180°
270°
0
2π
总结归纳
弧度制下角的集合与实数集的一一对应:
正角
零角
负角
任意角的集合
正实数
0
负实数
实数集R
知识点3:弧度制下的弧长公式和扇形面积公式
角度制 弧度制
弧长公式
扇形面积公式
l =
S = lR =
l = |α|·R
S = lR = ·|α|·R2
例 5 :若用R表示圆的半径,n( 0<n<360° ),α(0<α<2π)为圆心角,l是扇形弧长,S是扇形面积;结合前面所学,完成下面的表格:
注意:弧度制下的扇形面积公式中的角都要用弧度数,不能用度数.
1.用角度制、弧度制下的弧长公式,计算半径为1 m的圆中,60°的圆心角所对的弧的长度(可用计算工具)
练一练
解:角度制:l = = = m;
弧度制:60°= ;l = |α|·R = ×1= m;
发现:弧度制下的弧长公式形式变简单了,当熟练掌握角度、弧度互化后,还将进一步看到弧度制带来的便利.
2.如图,已知扇形AOB的圆心角为120°,半径长为6,求扇形AOB的面积.
练一练
解:扇形面积:S = lR = ·|α|·R2 = ××62 = 12π .
根据今天所学,回答下列问题:
(1)什么叫 1 弧度角
(2)说一说,“角度制”与“弧度制”的联系与区别;
(3)弧度制下的弧长公式与扇形面积公式.
5.1 任意角与弧度制
5.1.2 弧度制
1. 通过类比不同度量制,了解弧度制的概念;
2. 掌握弧度与角度的互化;
3. 掌握并能运用弧度制下的弧长公式和扇形面积公式;
问题 1:结合生活中常见的汽车仪表盘,说一说,图中两圈不同数字的含义?
拓展:外圈数字单位是“千米/小时” ;
内圈数字是英制,单位为“英里/小时”.
思考:参照上述事例,说一说,角的度量是否也能用不同的单位制呢?
知识点1:弧度制的概念
回顾:用度作单位来度量角的单位制叫做角度制;
如图,设a=n°,OP=r,点P所形成的圆弧 的长为l ;则:
PP1
O
A
B
α
P
P1
l =
思考:说一说,弧长与半径之间存在怎样的关系?
问题 2 :如图,在射线OA上任取一点Q(不同于点O),OQ=r1,在旋转过程中,点Q所形成的圆弧QQ1的长为l1. l1与r1的比值是多少?你能得出什么结论?
O
A
B
α
P
P1
Q1
Q
= n
由:l1 = ,得:
结论:圆心角α所对的弧长与半径的比值,只与α的大小有关;
即:这个比值随α的确定而唯一确定.
概念讲解
前提:圆心角α一定时,其所对的弧长与半径的比值一定,故可以用圆的弧长与半径的关系度量圆心角;
规定:长度等于半径长的圆弧所对的圆心角叫做 1 弧度的角;
弧度单位用符号rad表示,读作弧度;
用弧度作单位来度量角的单位制叫做弧度制;
例:如图,在单位圆(半径为1的圆)O中,AB的长
等于1,∠AOB就是1弧度的角.
x
y
O
A
B
1 rad
1
根据上述规定,在半径为 r 的圆中,弧长为 l 的弧所对的圆心角为 α rad,那么:
|α| = = n .
注意:
(1)类似角的正负,角的终边逆时针旋转 α 为正,顺时针旋转 α 为负;
(2)角的终边旋转超过一周后,可得弧度数大于2π或小于-2π的角;
即可用弧度表示任意大小的角;
(3)正角的弧度数是正数,负角的弧度数是负数,零角的弧度数是0.
例 2 :通过对比角度制与弧度制的区别与联系,完成下列表格.
弧度制 角度制
区别
联系
无论弧度制还是角度制,
角的大小都是一个与半径大小无关的定值
弧度制以线段长度来度量角
角度制是“以角量角”
弧度制是十进制
角度制是六十进制
1弧度是等于半径长的弧
所对的圆心角的大小
1°的角是周角的
思考:结合前面的汽车仪表盘事例,我们可以知道千米和英里之间存在一定的换算关系,那么角度制、弧度制之间也存在这样的换算关系吗?如果存在,又该如何换算呢?
知识点2:角度与弧度的换算
x
y
O
由 |α| = 可知,周角的弧度数为:α = = 2π rad;
故 360° = 2π rad, 180° = π rad.
注意:上述 180° 是对应 π rad,而不是对应 实数 π.
角度与弧度的换算公式:
180°= π rad
1°= rad ≈ 0.017 45 rad
1 rad = ()°≈ 57.30°
角度数 = 弧度数× ()°
弧度数 = 角度数×
例 3 :运用角度与弧度的换算公式,把下列角度化成弧度.
(1)22°30 ; (2)-210°(精确到0.001).
解:(1)∵ 22°30 = 22.5°,∴ 22.5°= 22.5× = 0.125 π;
(2) -210° = -210× = -1.167 π rad.
注意:
(1)角度中含有 分( )、秒( ) 时,化成弧度制之前,要先化成 度(°);
(2)负角换算成弧度后仍旧是一个负数.
例 4 :把下列弧度化成角度.
(1); (2)-.
解:(1) × ()°= 15°;
(2)- × ()°= -240°.
练一练
度 0° 30° 45° 120° 135° 150° 360°
弧度 π
1.运用换算公式,填写下列特殊角的度数与弧度数的对应表:
90°
60°
180°
270°
0
2π
总结归纳
弧度制下角的集合与实数集的一一对应:
正角
零角
负角
任意角的集合
正实数
0
负实数
实数集R
知识点3:弧度制下的弧长公式和扇形面积公式
角度制 弧度制
弧长公式
扇形面积公式
l =
S = lR =
l = |α|·R
S = lR = ·|α|·R2
例 5 :若用R表示圆的半径,n( 0<n<360° ),α(0<α<2π)为圆心角,l是扇形弧长,S是扇形面积;结合前面所学,完成下面的表格:
注意:弧度制下的扇形面积公式中的角都要用弧度数,不能用度数.
1.用角度制、弧度制下的弧长公式,计算半径为1 m的圆中,60°的圆心角所对的弧的长度(可用计算工具)
练一练
解:角度制:l = = = m;
弧度制:60°= ;l = |α|·R = ×1= m;
发现:弧度制下的弧长公式形式变简单了,当熟练掌握角度、弧度互化后,还将进一步看到弧度制带来的便利.
2.如图,已知扇形AOB的圆心角为120°,半径长为6,求扇形AOB的面积.
练一练
解:扇形面积:S = lR = ·|α|·R2 = ××62 = 12π .
根据今天所学,回答下列问题:
(1)什么叫 1 弧度角
(2)说一说,“角度制”与“弧度制”的联系与区别;
(3)弧度制下的弧长公式与扇形面积公式.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
