5.5.2 第1课时 简单的三角恒等变换 课件(共13张PPT) 2023-2024学年高一数学人教A版(2019)必修第一册
文档属性
| 名称 | 5.5.2 第1课时 简单的三角恒等变换 课件(共13张PPT) 2023-2024学年高一数学人教A版(2019)必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 661.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-05 00:00:00 | ||
图片预览





文档简介
(共13张PPT)
5.5.2.1 简单的三角恒等变换
1. 能用倍角公式导出半角公式,掌握三角恒等变换的基本方法;
2. 能利用三角恒等变换对三角函数式求值以及三角恒等式的证明.
知识点 1 :倍角公式的简单变形
回顾:按照相应规律,结合“倍”角的概念,说说 α 与 有什么关系?
α 是 的二倍
例 1 :试以 cos α 表示 sin2,cos2,tan2 .
解:α 是 的二倍角,在倍角公式 cos 2α = 1 2sin2α 中,
以 α 代替 2α,以 代替 α 得:cos α = 1 2sin2 ,所以 sin2 = ①;
同理:根据倍角公式 cos 2α = 2cos2α 1得:cos2 = ②;
将①②两个等式的左右两边分别相除得:tan2 = .
思考:若 cos α = ,你能求出 sin ,cos ,tan 的值吗?
由例 1 可知:sin2 = ,cos2 = ,tan2 = ;
思考:若 cos α = ,你能求出 sin ,cos ,tan 的值吗?
由上式可得:sin =±,cos =±,tan =± ;
将 cos α = 分别带入即可求出 sin ,cos ,tan 的值.
总结归纳
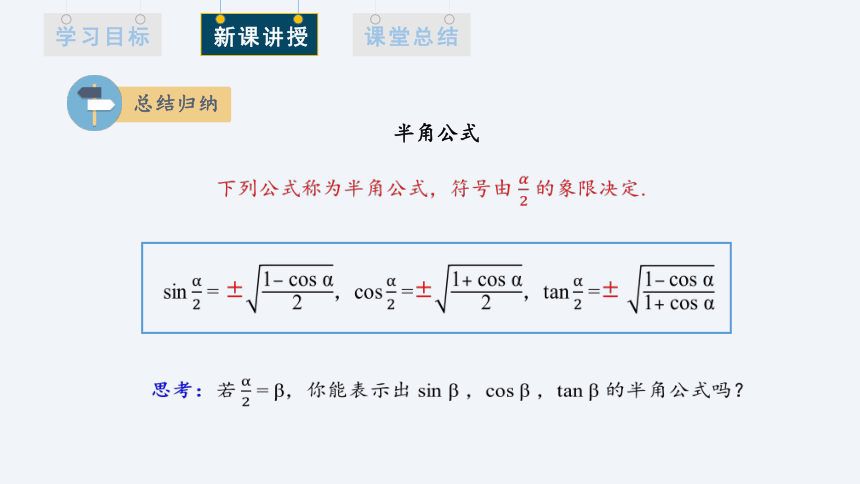
半角公式
下列公式称为半角公式,符号由 的象限决定.
sin = ±,cos =±,tan =±
思考:若 = β,你能表示出 sin β ,cos β ,tan β 的半角公式吗?
降幂与升幂公式
sin2β = ,cos2β = ,tan2β =
降幂公式
半角公式:
cos 2β = cos2β – sin2β = 2cos2β – 1 = 1 – 2sin2β;
tan 2β = ;
升幂公式
倍角公式:
总结归纳
练一练
C
1. 若 cos α = ,α∈(0,π),则 cos 的值为( )
A. B. C. D.
例 2:先求证,再说说下列两个式子的左右两边在结构形式上有什么不同.
(1)sin α·cos β = [sin (α+β) + sin (α – β)];
(2)sin θ + sin φ = 2 sin · cos .
知识点 2 :三角恒等式的证明
证明:(1)因为 sin (α + β) = sin α·cos β + cos α·sin β,
sin (α – β) = sin α·cos β – cos α·sin β,
将以上两式的左右两边分别相加,得 sin (α + β) + sin (α – β) = 2sin α·cos β ①,
即 sin α·cos β = [sin (α+β) + sin (α – β)],故(1)得证;
求证:(2)sin θ + sin φ = 2 sin · cos .
证明:(2)由(1)可得:sin (α + β) + sin (α – β) = 2sin α·cos β ① ,
设:α = ,β = ,把 α、β 带入 ① 中,
即得:sin θ + sin φ = 2 sin · cos ,故(2)得证;
思考:上面两个式子的左右两边在结构形式上有什么不同?
练一练
2. 参照例题,证明下列式子.
(1)cos α·cos β = [cos(α+β)+cos(α–β)];(2)cos θ+cos φ = 2coscos .
思考:结合上述证明,你还能发现其他类似的式子吗?
总结归纳
积化和差与和差化积公式
(1)sin α·cos β = [sin(α + β) + sin(α – β)];
(2)cos α·sin β = [sin(α + β) – sin(α – β)];
(3)cos α·cos β = [cos(α + β) + cos(α – β)];
(4)sin α·sin β = – [cos(α + β) – cos(α – β)].
积化和差
(1)sin θ + sin φ = 2sin cos;
(2)sin θ – sin φ = 2cos sin;
(3)cos θ + cos φ = 2cos cos;
(4)cos θ – cos φ = –2sin sin.
和差化积
根据今天所学,回答下列问题:
(1)说说你对倍角公式和半角公式间相互转化关系的理解;
(2)说说你对积化和差与和差化积公式的理解.
5.5.2.1 简单的三角恒等变换
1. 能用倍角公式导出半角公式,掌握三角恒等变换的基本方法;
2. 能利用三角恒等变换对三角函数式求值以及三角恒等式的证明.
知识点 1 :倍角公式的简单变形
回顾:按照相应规律,结合“倍”角的概念,说说 α 与 有什么关系?
α 是 的二倍
例 1 :试以 cos α 表示 sin2,cos2,tan2 .
解:α 是 的二倍角,在倍角公式 cos 2α = 1 2sin2α 中,
以 α 代替 2α,以 代替 α 得:cos α = 1 2sin2 ,所以 sin2 = ①;
同理:根据倍角公式 cos 2α = 2cos2α 1得:cos2 = ②;
将①②两个等式的左右两边分别相除得:tan2 = .
思考:若 cos α = ,你能求出 sin ,cos ,tan 的值吗?
由例 1 可知:sin2 = ,cos2 = ,tan2 = ;
思考:若 cos α = ,你能求出 sin ,cos ,tan 的值吗?
由上式可得:sin =±,cos =±,tan =± ;
将 cos α = 分别带入即可求出 sin ,cos ,tan 的值.
总结归纳
半角公式
下列公式称为半角公式,符号由 的象限决定.
sin = ±,cos =±,tan =±
思考:若 = β,你能表示出 sin β ,cos β ,tan β 的半角公式吗?
降幂与升幂公式
sin2β = ,cos2β = ,tan2β =
降幂公式
半角公式:
cos 2β = cos2β – sin2β = 2cos2β – 1 = 1 – 2sin2β;
tan 2β = ;
升幂公式
倍角公式:
总结归纳
练一练
C
1. 若 cos α = ,α∈(0,π),则 cos 的值为( )
A. B. C. D.
例 2:先求证,再说说下列两个式子的左右两边在结构形式上有什么不同.
(1)sin α·cos β = [sin (α+β) + sin (α – β)];
(2)sin θ + sin φ = 2 sin · cos .
知识点 2 :三角恒等式的证明
证明:(1)因为 sin (α + β) = sin α·cos β + cos α·sin β,
sin (α – β) = sin α·cos β – cos α·sin β,
将以上两式的左右两边分别相加,得 sin (α + β) + sin (α – β) = 2sin α·cos β ①,
即 sin α·cos β = [sin (α+β) + sin (α – β)],故(1)得证;
求证:(2)sin θ + sin φ = 2 sin · cos .
证明:(2)由(1)可得:sin (α + β) + sin (α – β) = 2sin α·cos β ① ,
设:α = ,β = ,把 α、β 带入 ① 中,
即得:sin θ + sin φ = 2 sin · cos ,故(2)得证;
思考:上面两个式子的左右两边在结构形式上有什么不同?
练一练
2. 参照例题,证明下列式子.
(1)cos α·cos β = [cos(α+β)+cos(α–β)];(2)cos θ+cos φ = 2coscos .
思考:结合上述证明,你还能发现其他类似的式子吗?
总结归纳
积化和差与和差化积公式
(1)sin α·cos β = [sin(α + β) + sin(α – β)];
(2)cos α·sin β = [sin(α + β) – sin(α – β)];
(3)cos α·cos β = [cos(α + β) + cos(α – β)];
(4)sin α·sin β = – [cos(α + β) – cos(α – β)].
积化和差
(1)sin θ + sin φ = 2sin cos;
(2)sin θ – sin φ = 2cos sin;
(3)cos θ + cos φ = 2cos cos;
(4)cos θ – cos φ = –2sin sin.
和差化积
根据今天所学,回答下列问题:
(1)说说你对倍角公式和半角公式间相互转化关系的理解;
(2)说说你对积化和差与和差化积公式的理解.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
