5.6.2 函数 y=Asin(ωx+φ) 的图象-2023-2024学年高二数学(沪教版2020选择性必修第一册) 课件(共16张PPT)
文档属性
| 名称 | 5.6.2 函数 y=Asin(ωx+φ) 的图象-2023-2024学年高二数学(沪教版2020选择性必修第一册) 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-11 07:05:21 | ||
图片预览





文档简介
(共16张PPT)
5.6.2 函数 y = Asin(ωx + φ) 的图象
1. 掌握参数 A、ω、φ 对函数 y = Asin(ωx + φ) 的图象的影响,理解参数 A、ω、φ 在圆周运动中的实际意义;
2. 理解从正弦曲线到函数 y = Asin(ωx + φ) 图象的变换过程,能用“五点法”画函数 y = Asin(ωx + φ) 的图象.
知识点 1 :参数 A、ω、φ 对函数 y = Asin(ωx + φ) 图象的影响
回顾:利用三角函数的知识,我们构建了一个形如 y = Asin(ωx + φ) 的函数;观察可知,这个函数由参数 A,ω,φ 所确定.
思考:观察函数 y = sin x 的解析式,说说它与函数 y = Asin(ωx + φ) 的解析有何区别?
当函数 y = Asin(ωx + φ) 的参数 A,ω,φ 都为 1 时,函数即为 y = sin x.
思考:能否借助函数 y = sin x 的图象与性质来研究参数 A,ω,φ 对函数 y = Asin(ωx + φ) 的影响?
(1)探索 φ 对 y = sin(x + φ) 图象的影响:
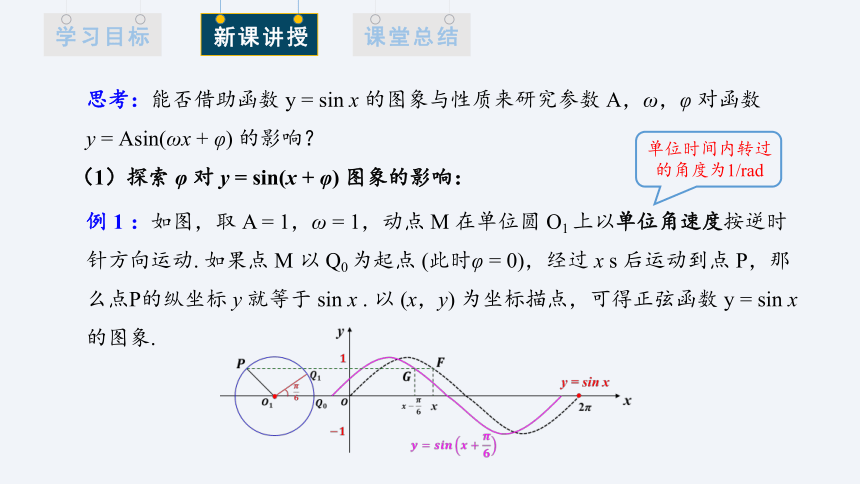
例 1 :如图,取 A = 1,ω = 1,动点 M 在单位圆 O1 上以单位角速度按逆时针方向运动. 如果点 M 以 Q0 为起点 (此时φ = 0),经过 x s 后运动到点 P,那么点P的纵坐标 y 就等于 sin x . 以 (x,y) 为坐标描点,可得正弦函数 y = sin x的图象.
单位时间内转过的角度为1/rad
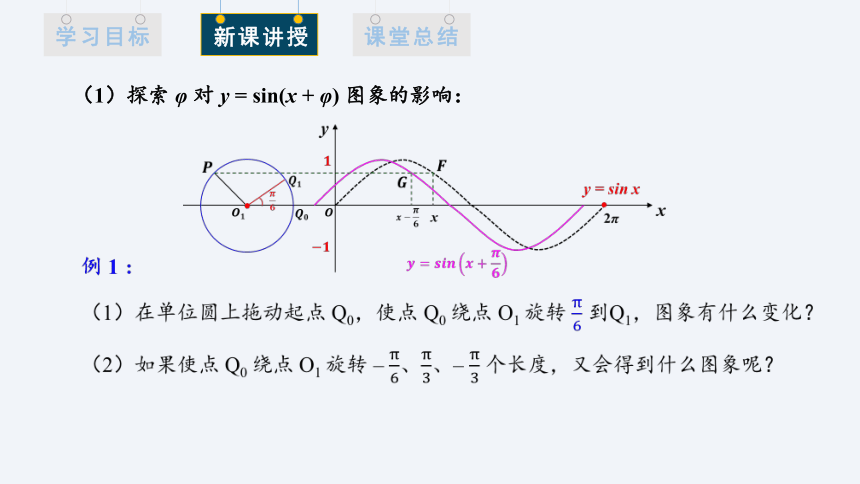
(1)探索 φ 对 y = sin(x + φ) 图象的影响:
例 1 :
(1)在单位圆上拖动起点 Q0,使点 Q0 绕点 O1 旋转 到Q1,图象有什么变化?
(2)如果使点 Q0 绕点 O1 旋转 – 、、– 个长度,又会得到什么图象呢?
参数 φ 对 y = sin(x + φ) 图象的影响
归纳小结 1
① 把正弦曲线上的所有点向左(当φ > 0时)或向右(当φ < 0时)平移 |φ| 个单位长度,就得到函数 y = sin(x + φ) 的图象;
② φ 的变化只改变图象的左右变化,形状、大小完全不变;
③ 这种变化引起的是初始位置的变换,一般称为相位变换.
(2)探索 ω ( ω > 0 ) 对 y = sin(ωx + φ) 图象的影响:
例 2 :如图,取圆的半径 A = 1,令 φ = ,当 ω = 1时,y = sin ( x + )的图象.
(1)取 ω = 2 时,函数的图象有什么变化?
(2)取 ω = ,3,,图象又有什么变化?若 ω 取任意正数呢?
参数 ω ( ω > 0 ) 对 y = sin(ωx + φ) 图象的影响
归纳小结 2
① ω 的作用:引起周期 T = 的改变,这种变换叫做横向伸缩;
② ω 的变化引起的横向伸缩,会导致图象形状改变(被横向拉长或缩短);
③ ω > 1 时,函数 y = sin(ωx + φ) 的图象相比函数 y = sin(x + φ) 横向缩短,周期变小;
0 < ω < 1 时,函数 y = sin(ωx + φ) 的图象相比函数 y = sin(x + φ) 横向伸长,周期变大;
(3)探索 A ( A > 0 ) 对 y = Asin(ωx + φ) 图象的影响:
例 3 :如图,令 ω = 2,φ = ,当 A = 1 时,y = sin ( 2x + )的图象.
(1)改变A的取值,令 A 取 2,,3, 时,函数的图象有什么变化?
(2)若 A 取任意正数,函数的图象有什么变化?
参数 A ( A > 0 ) 对 y = Asin(ωx + φ) 图象的影响
归纳小结 3
① A 的作用:引起值域的改变,这种变换叫做纵向伸缩;
② A 的变化引起的纵向伸缩,会导致图象形状改变(被纵向拉长或缩短);
③ 若 A > 0,则函数 y = Asin(ωx + φ) 的值域为[ – A,A];
若 A < 0,则函数 y = Asin(ωx + φ) 的值域为[ A,– A ];
参数 A、ω、φ 对函数 y = Asin(ωx + φ) 图象的影响
归纳总结
参数 变换情况 对函数 y = Asin (ωx + φ) 图象的影响
φ 相位变换 左右平移,图象形状、大小完全不变
ω 横向伸缩变换 T = ,周期变化,图象形状横向拉长或缩短
A 纵向伸缩变换 值域变化,图象形状纵向拉长或缩短
参数 A、ω、φ 变化对函数 y = Asin(ωx + φ) 图象的变化
相位变换
横向伸缩
纵向伸缩
y = sin x
知识点 2 :用“五点法”画函数 y = Asin (ωx + φ) 的图象
例 4 :用“五点法”画出函数 y = 2sin (3x – ) 的简图.
分析:① 先画出 y = sin x 的图象;
② 将正弦曲线向右平移 个单位长度,得函数 y = sin (x – ) 的图象;
③ 曲线上各点的横坐标变为原来的 倍,得函数 y = sin (3x – ) 的图象;
④ 曲线上各点的纵坐标变为原来的 2 倍,即得到 y = 2sin (3x – ) 的图象.
用“五点法”画函数 y = 2sin (3x – ) 在一个周期 ( ) 内的图象;
令 X = 3x – , 则x = ( X + ),列表,描点画图:
练一练
1. 请用“五点法”画出下列函数的简图.
解:
根据今天所学,回答下列问题:
三个参数 A、ω、φ 对函数 y = Asin(ωx + φ) 图象的分别有什么影响?
5.6.2 函数 y = Asin(ωx + φ) 的图象
1. 掌握参数 A、ω、φ 对函数 y = Asin(ωx + φ) 的图象的影响,理解参数 A、ω、φ 在圆周运动中的实际意义;
2. 理解从正弦曲线到函数 y = Asin(ωx + φ) 图象的变换过程,能用“五点法”画函数 y = Asin(ωx + φ) 的图象.
知识点 1 :参数 A、ω、φ 对函数 y = Asin(ωx + φ) 图象的影响
回顾:利用三角函数的知识,我们构建了一个形如 y = Asin(ωx + φ) 的函数;观察可知,这个函数由参数 A,ω,φ 所确定.
思考:观察函数 y = sin x 的解析式,说说它与函数 y = Asin(ωx + φ) 的解析有何区别?
当函数 y = Asin(ωx + φ) 的参数 A,ω,φ 都为 1 时,函数即为 y = sin x.
思考:能否借助函数 y = sin x 的图象与性质来研究参数 A,ω,φ 对函数 y = Asin(ωx + φ) 的影响?
(1)探索 φ 对 y = sin(x + φ) 图象的影响:
例 1 :如图,取 A = 1,ω = 1,动点 M 在单位圆 O1 上以单位角速度按逆时针方向运动. 如果点 M 以 Q0 为起点 (此时φ = 0),经过 x s 后运动到点 P,那么点P的纵坐标 y 就等于 sin x . 以 (x,y) 为坐标描点,可得正弦函数 y = sin x的图象.
单位时间内转过的角度为1/rad
(1)探索 φ 对 y = sin(x + φ) 图象的影响:
例 1 :
(1)在单位圆上拖动起点 Q0,使点 Q0 绕点 O1 旋转 到Q1,图象有什么变化?
(2)如果使点 Q0 绕点 O1 旋转 – 、、– 个长度,又会得到什么图象呢?
参数 φ 对 y = sin(x + φ) 图象的影响
归纳小结 1
① 把正弦曲线上的所有点向左(当φ > 0时)或向右(当φ < 0时)平移 |φ| 个单位长度,就得到函数 y = sin(x + φ) 的图象;
② φ 的变化只改变图象的左右变化,形状、大小完全不变;
③ 这种变化引起的是初始位置的变换,一般称为相位变换.
(2)探索 ω ( ω > 0 ) 对 y = sin(ωx + φ) 图象的影响:
例 2 :如图,取圆的半径 A = 1,令 φ = ,当 ω = 1时,y = sin ( x + )的图象.
(1)取 ω = 2 时,函数的图象有什么变化?
(2)取 ω = ,3,,图象又有什么变化?若 ω 取任意正数呢?
参数 ω ( ω > 0 ) 对 y = sin(ωx + φ) 图象的影响
归纳小结 2
① ω 的作用:引起周期 T = 的改变,这种变换叫做横向伸缩;
② ω 的变化引起的横向伸缩,会导致图象形状改变(被横向拉长或缩短);
③ ω > 1 时,函数 y = sin(ωx + φ) 的图象相比函数 y = sin(x + φ) 横向缩短,周期变小;
0 < ω < 1 时,函数 y = sin(ωx + φ) 的图象相比函数 y = sin(x + φ) 横向伸长,周期变大;
(3)探索 A ( A > 0 ) 对 y = Asin(ωx + φ) 图象的影响:
例 3 :如图,令 ω = 2,φ = ,当 A = 1 时,y = sin ( 2x + )的图象.
(1)改变A的取值,令 A 取 2,,3, 时,函数的图象有什么变化?
(2)若 A 取任意正数,函数的图象有什么变化?
参数 A ( A > 0 ) 对 y = Asin(ωx + φ) 图象的影响
归纳小结 3
① A 的作用:引起值域的改变,这种变换叫做纵向伸缩;
② A 的变化引起的纵向伸缩,会导致图象形状改变(被纵向拉长或缩短);
③ 若 A > 0,则函数 y = Asin(ωx + φ) 的值域为[ – A,A];
若 A < 0,则函数 y = Asin(ωx + φ) 的值域为[ A,– A ];
参数 A、ω、φ 对函数 y = Asin(ωx + φ) 图象的影响
归纳总结
参数 变换情况 对函数 y = Asin (ωx + φ) 图象的影响
φ 相位变换 左右平移,图象形状、大小完全不变
ω 横向伸缩变换 T = ,周期变化,图象形状横向拉长或缩短
A 纵向伸缩变换 值域变化,图象形状纵向拉长或缩短
参数 A、ω、φ 变化对函数 y = Asin(ωx + φ) 图象的变化
相位变换
横向伸缩
纵向伸缩
y = sin x
知识点 2 :用“五点法”画函数 y = Asin (ωx + φ) 的图象
例 4 :用“五点法”画出函数 y = 2sin (3x – ) 的简图.
分析:① 先画出 y = sin x 的图象;
② 将正弦曲线向右平移 个单位长度,得函数 y = sin (x – ) 的图象;
③ 曲线上各点的横坐标变为原来的 倍,得函数 y = sin (3x – ) 的图象;
④ 曲线上各点的纵坐标变为原来的 2 倍,即得到 y = 2sin (3x – ) 的图象.
用“五点法”画函数 y = 2sin (3x – ) 在一个周期 ( ) 内的图象;
令 X = 3x – , 则x = ( X + ),列表,描点画图:
练一练
1. 请用“五点法”画出下列函数的简图.
解:
根据今天所学,回答下列问题:
三个参数 A、ω、φ 对函数 y = Asin(ωx + φ) 图象的分别有什么影响?
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
