3.1.2 函数的表示法 第2课时-2023-2024学年高二数学(沪教版2020选择性必修第一册) 课件(共18张PPT)
文档属性
| 名称 | 3.1.2 函数的表示法 第2课时-2023-2024学年高二数学(沪教版2020选择性必修第一册) 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 376.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-11 07:07:59 | ||
图片预览






文档简介
(共18张PPT)
3.1.2 函数的表示法
第2课时
1.能选择恰当的方法表示实际问题中的函数关系
2.会求分段函数的值
3.掌握函数解析式求解方法
回顾:上节课学习了函数的三种表示方法,它们各自的特点是什么?
各表示方法是否存在局限性呢?
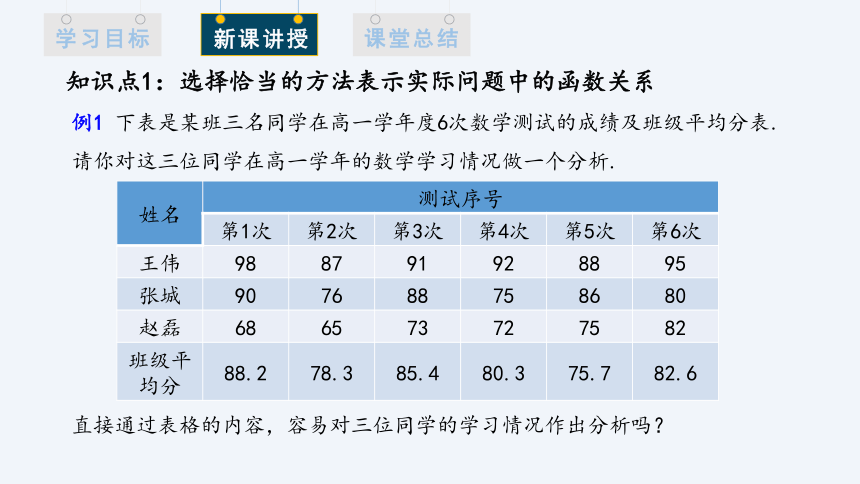
例1 下表是某班三名同学在高一学年度6次数学测试的成绩及班级平均分表.请你对这三位同学在高一学年的数学学习情况做一个分析.
知识点1:选择恰当的方法表示实际问题中的函数关系
直接通过表格的内容,容易对三位同学的学习情况作出分析吗?
姓名 测试序号
第1次 第2次 第3次 第4次 第5次 第6次
王伟 98 87 91 92 88 95
张城 90 76 88 75 86 80
赵磊 68 65 73 72 75 82
班级平均分 88.2 78.3 85.4 80.3 75.7 82.6
你会用什么方法表示“成绩”与“测试序号”之间的函数关系,为什么?
姓名 测试序号
第1次 第2次 第3次 第4次 第5次 第6次
王伟 98 87 91 92 88 95
张城 90 76 88 75 86 80
赵磊 68 65 73 72 75 82
班级平均分 88.2 78.3 85.4 80.3 75.7 82.6
为了更容易的看出学生的学习情况,将离散的点用虚线连接,方便比较,虚线不是函数图象的组成部分.
图象能直观地看到每位同学成绩变化的情况,对分析很有帮助.
张诚同学的数学成绩不稳定,总是在班级平均水平上下波动,而且幅度较大.
赵磊同学的数学成绩低于平均水平,但是他的成绩呈曲线上升的趋势,从而表明他的数学成绩在稳步提高.
王伟同学的数学成绩始终高于班级平均水平,学习情况比较稳定而且比较优秀.
解析、列表和图象三法各有缺点,面对实际问题时根据需要恰当选择
表示法 优点 缺点
解析法 变量关系特别明显,给定任意自变量可直接求出对应的函数值. 不形象,不直观,变化趋势难判断,有些函数无法使用.
列表法 不用计算,只需看任意给定变量值,表中查找很容易. 受变量数量限制,只限数量不多时使用.
图象法 直观形象的展示变化趋势. 近似表达对应值,误差较大,容易误判.
归纳总结
例2 某地居民用电采用阶梯电价,其标准如下:每户每月用电量不超过180千瓦时的部分,每千瓦时电费是0.6元;每户每月用电量超过180千瓦时,但不超过350千瓦时的部分,每千瓦时电费是0.65元:每户每月用电量超过350千瓦时的部分,每千瓦时电费是0.9元,某月某户居民交电费y元,已知该户居民该月用电量为x千瓦时.
(1)求y关于x的函数关系式;
解(1)依据题意可知为分段函数,
知识点2:分段函数求值
(2)若该户居民该月交电费199元,求该户居民该月的用电量.
(2)当0≤x≤180时,对应函数关系式是:y=0.6x,可得 0≤0.6x≤108,
即该户居民该月的用电量为320千瓦时.
则y=0.65x-9=199,解得x=320,
因为108<199<218.5,所以180<x≤350,
当x>350时,对应函数关系式是:y=0.9x-96.5,可得 6.50.9x-96.5>218.5,
当180<x≤350时,对应函数关系式是:y=0.65x-9,可得 108<0.65x-9≤218.5,
归纳总结
1.求分段函数的函数值的方法
(1)确定要求值的自变量属于哪一段区间.
(2)代入该段的解析式求值,直到求出值为止.
2.求某条件下自变量的值的方法,先假设所求的值在分段函数定义区间的各段上,然后相应求出自变量的值,切记代入检验.
为了鼓励小强勤做家务,培养他的劳动意识,小强每月的生活费用都是根据上月他的家务劳动时间所得奖励加上基本生活费从父母那里获取的.若设小强每月的家务劳动时间为x小时,该月可得(即下月他可获得)的总费用为y(元),则y(元)和x(小时)之间的函数图象如图所示.
练一练
解:(1)由题意可得
O
240
200
150
y(元)
20
30
x(小时)
10
(1)根据图象,写出函数解析式.
(2)若小强5月份希望有250元费用,则小强4月份需做家务多少小时?
(2)当x≥20时,y与x的函数关系式是:y=4x+120
代入相应函数关系式可得 x =32.5
答:当小强4月份家务劳动32.5小时,5月份可得到的费用为250元.
O
240
200
150
y(元)
20
30
x(小时)
10
例3 已知一次函数 f(x)满足f( f(x)) = 4x+6,求 f(x)的解析式.
解:由题意设 f(x) = ax+b (a ≠ 0)
知识点3:求解函数解析式
则 f(f(x))= f(ax+b)= a(ax+b)+b = a2x+ab+b = 4x+6
所以 解得 或
所以 f(x) =2x+2 或 f(x) = -2x-6
已知函数类型时,可设其解析式的形式,根据已知条件建立关于待定系数的方程,从而求出函数解析式.
1.已知 y = f(x) 为一次函数,且满足 3 f(1+x)-2 f(1-x) =4x+3 ,求 f(x)的解析式.
解:由题意设 f(x) =ax+b (a ≠ 0) ,
则由 3 f(1+x)-2 f(1-x) =4x+3,
得 3[a(x+1)+b]-2[a(1-x)+b]= 4x+3 ,
即 (5a-4)x+a+b-3= 0,
故 解得
所以
练一练
2.已知 ,求 f(x)的解析式.
解:由题意令 ,
则 x= (t -1)2 ,t≥1
所以 f(x) =x2-1 (x≥1)
所以 f(t)= (t-1)2 +2(t-1) = t2-1 (t≥1)
当f作用于式子时,可用换元法求解函数解析式.
3.已知函数 ,求 f(x)的解析式.
解:已知等式中,将x换成 ,得
与已知方程联立,得 ,
消去
所以
当已知中含有f(x),f(-x)或 时,可用消元法求解函数解析式.
根据今天所学,回答下列问题:
1.如何选择函数的表示方法?
2.怎么求分段函数的值?
3.求解函数解析式的方法有哪些?
3.1.2 函数的表示法
第2课时
1.能选择恰当的方法表示实际问题中的函数关系
2.会求分段函数的值
3.掌握函数解析式求解方法
回顾:上节课学习了函数的三种表示方法,它们各自的特点是什么?
各表示方法是否存在局限性呢?
例1 下表是某班三名同学在高一学年度6次数学测试的成绩及班级平均分表.请你对这三位同学在高一学年的数学学习情况做一个分析.
知识点1:选择恰当的方法表示实际问题中的函数关系
直接通过表格的内容,容易对三位同学的学习情况作出分析吗?
姓名 测试序号
第1次 第2次 第3次 第4次 第5次 第6次
王伟 98 87 91 92 88 95
张城 90 76 88 75 86 80
赵磊 68 65 73 72 75 82
班级平均分 88.2 78.3 85.4 80.3 75.7 82.6
你会用什么方法表示“成绩”与“测试序号”之间的函数关系,为什么?
姓名 测试序号
第1次 第2次 第3次 第4次 第5次 第6次
王伟 98 87 91 92 88 95
张城 90 76 88 75 86 80
赵磊 68 65 73 72 75 82
班级平均分 88.2 78.3 85.4 80.3 75.7 82.6
为了更容易的看出学生的学习情况,将离散的点用虚线连接,方便比较,虚线不是函数图象的组成部分.
图象能直观地看到每位同学成绩变化的情况,对分析很有帮助.
张诚同学的数学成绩不稳定,总是在班级平均水平上下波动,而且幅度较大.
赵磊同学的数学成绩低于平均水平,但是他的成绩呈曲线上升的趋势,从而表明他的数学成绩在稳步提高.
王伟同学的数学成绩始终高于班级平均水平,学习情况比较稳定而且比较优秀.
解析、列表和图象三法各有缺点,面对实际问题时根据需要恰当选择
表示法 优点 缺点
解析法 变量关系特别明显,给定任意自变量可直接求出对应的函数值. 不形象,不直观,变化趋势难判断,有些函数无法使用.
列表法 不用计算,只需看任意给定变量值,表中查找很容易. 受变量数量限制,只限数量不多时使用.
图象法 直观形象的展示变化趋势. 近似表达对应值,误差较大,容易误判.
归纳总结
例2 某地居民用电采用阶梯电价,其标准如下:每户每月用电量不超过180千瓦时的部分,每千瓦时电费是0.6元;每户每月用电量超过180千瓦时,但不超过350千瓦时的部分,每千瓦时电费是0.65元:每户每月用电量超过350千瓦时的部分,每千瓦时电费是0.9元,某月某户居民交电费y元,已知该户居民该月用电量为x千瓦时.
(1)求y关于x的函数关系式;
解(1)依据题意可知为分段函数,
知识点2:分段函数求值
(2)若该户居民该月交电费199元,求该户居民该月的用电量.
(2)当0≤x≤180时,对应函数关系式是:y=0.6x,可得 0≤0.6x≤108,
即该户居民该月的用电量为320千瓦时.
则y=0.65x-9=199,解得x=320,
因为108<199<218.5,所以180<x≤350,
当x>350时,对应函数关系式是:y=0.9x-96.5,可得 6.50.9x-96.5>218.5,
当180<x≤350时,对应函数关系式是:y=0.65x-9,可得 108<0.65x-9≤218.5,
归纳总结
1.求分段函数的函数值的方法
(1)确定要求值的自变量属于哪一段区间.
(2)代入该段的解析式求值,直到求出值为止.
2.求某条件下自变量的值的方法,先假设所求的值在分段函数定义区间的各段上,然后相应求出自变量的值,切记代入检验.
为了鼓励小强勤做家务,培养他的劳动意识,小强每月的生活费用都是根据上月他的家务劳动时间所得奖励加上基本生活费从父母那里获取的.若设小强每月的家务劳动时间为x小时,该月可得(即下月他可获得)的总费用为y(元),则y(元)和x(小时)之间的函数图象如图所示.
练一练
解:(1)由题意可得
O
240
200
150
y(元)
20
30
x(小时)
10
(1)根据图象,写出函数解析式.
(2)若小强5月份希望有250元费用,则小强4月份需做家务多少小时?
(2)当x≥20时,y与x的函数关系式是:y=4x+120
代入相应函数关系式可得 x =32.5
答:当小强4月份家务劳动32.5小时,5月份可得到的费用为250元.
O
240
200
150
y(元)
20
30
x(小时)
10
例3 已知一次函数 f(x)满足f( f(x)) = 4x+6,求 f(x)的解析式.
解:由题意设 f(x) = ax+b (a ≠ 0)
知识点3:求解函数解析式
则 f(f(x))= f(ax+b)= a(ax+b)+b = a2x+ab+b = 4x+6
所以 解得 或
所以 f(x) =2x+2 或 f(x) = -2x-6
已知函数类型时,可设其解析式的形式,根据已知条件建立关于待定系数的方程,从而求出函数解析式.
1.已知 y = f(x) 为一次函数,且满足 3 f(1+x)-2 f(1-x) =4x+3 ,求 f(x)的解析式.
解:由题意设 f(x) =ax+b (a ≠ 0) ,
则由 3 f(1+x)-2 f(1-x) =4x+3,
得 3[a(x+1)+b]-2[a(1-x)+b]= 4x+3 ,
即 (5a-4)x+a+b-3= 0,
故 解得
所以
练一练
2.已知 ,求 f(x)的解析式.
解:由题意令 ,
则 x= (t -1)2 ,t≥1
所以 f(x) =x2-1 (x≥1)
所以 f(t)= (t-1)2 +2(t-1) = t2-1 (t≥1)
当f作用于式子时,可用换元法求解函数解析式.
3.已知函数 ,求 f(x)的解析式.
解:已知等式中,将x换成 ,得
与已知方程联立,得 ,
消去
所以
当已知中含有f(x),f(-x)或 时,可用消元法求解函数解析式.
根据今天所学,回答下列问题:
1.如何选择函数的表示方法?
2.怎么求分段函数的值?
3.求解函数解析式的方法有哪些?
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
