一元二次方程(1)

课件20张PPT。22.1 一元二次方程(1) 小区在每两幢楼之间，开辟面积为900平方米 的一块长方形绿地，并且长比宽多10米，则绿地的长和宽各为多少？问题一 分　析：设长方形绿地的宽为x米，不难列出方程
x(x＋10)＝900
整理可得
x2＋10x－900=0.　　（1） 小区在每两幢楼之间，开辟面积为900平方米 的一块长方形绿地，并且长比宽多10米，则绿地的长和宽各为多少？问 题 二整理得：x2-18x+45=0，设竹竿的长为x尺，可列得方程：问题三学校图书馆去年年底有图书5万册，预计到明年年底增加到7.2万册.求这两年的年平均增长率.分析：设这两年的年平均增长率为x，去年年底的图书数是5万册，则今年年底的图书数是5（1＋x）万册；同样，明年年底的图书数又是今年年底的（1＋x）倍，即5（1＋x）(1＋x)＝5(1＋x)2万册.可列得方程
5（1＋x）2=7.2,
整理可得
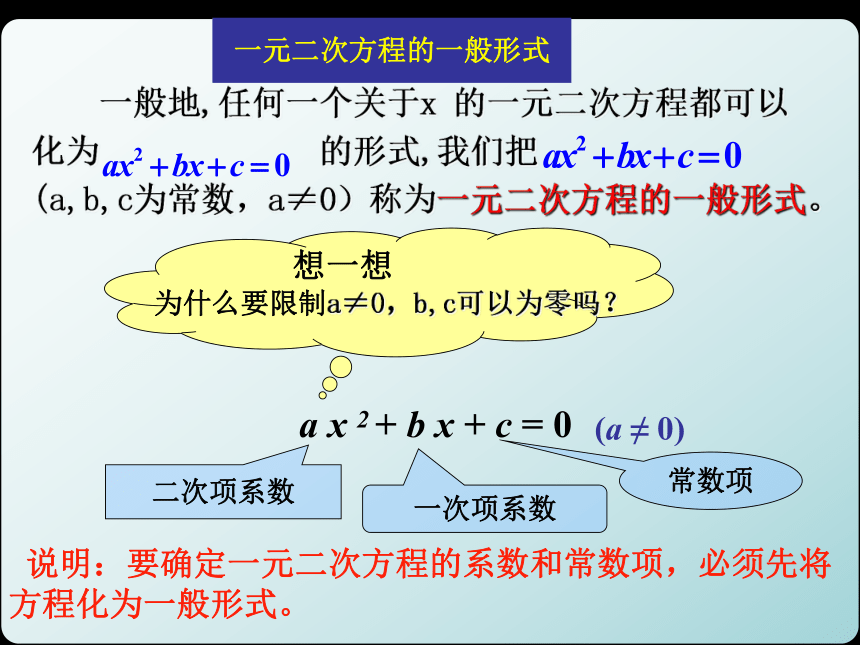
5x2＋10x－2.2=0.　　（2）这三个方程与一元一次方程的区别在哪里？它们有什么共同特点呢？ x2＋10x－900=0.　　（1）5x2＋10x－2.2=0.　　（3）x2-18x+45=0， （2）整式方程中都只含有一个未知数，并且未知数的最高次数是2，这样的方程叫做一元二次方程 .一元二次方程的概念: 一元二次方程的一般形式 一般地,任何一个关于x 的一元二次方程都可以
化为 的形式,我们把
(a,b,c为常数，a≠0）称为一元二次方程的一般形式。为什么要限制a≠0，b,c可以为零吗？想一想 a x 2 + b x + c = 0(a ≠ 0)二次项系数一次项系数常数项 说明：要确定一元二次方程的系数和常数项，必须先将方程化为一般形式。 例题讲解[例1]下列方程中哪些是一元二次方程？
试说明理由。
（1）
（2）
（3）
（4） [例2] 将下列方程化为一般形式，并分别指出它们的二次项系数、一次项系数和常数项： （x-2）(x+3)=8 1.2.3.练习:把下列方程化成一元二次方程的一般形式,并写出它的二次项系数,一次项系数和常数项.[例３]方程（2a—4）x2 —2bx+a=0, 在什么条件下此方程为一元二次方程？在什么条件下此方程为一元一次方程？ 解：当a≠2时是一元二次方程；
当a＝2，b≠0时是一元一次方程；［例4 ］已知关于x的一元二次方程
(m-1)x2+3x-5m+4=0有一根为2，求m。［分析］一根为2即x=2,只需把x=2代入原方程。
练习巩固1、将下列方程化为一般形式，并分别指出它们的二次项系数、一次项系数和常数项.
2x(x-1)=3(x-5)-4
2、关于x的方程
在什么条件下是一元二次方程？
在什么条件下是一元一次方程？1.下列方程中,无论a为何值,总是关于x的一元二次方程的是( )
A.(2x-1)(x2+3)=2x2-a B.ax2+2x+4=0
C.ax2+x=x2-1 D.(a2+1)x2=02.当m为何值时,方程

是关于x的一元二次方程.D 关于x的方程
是一元二次方程，求k的值。合作学习:已列出下列问题中关于未知数x的方程:(1)把面积为4平方米的一张纸分割成如图所示的正方形和长方形两个部分,求正方形的边长.
设正方形的边长为x,可列出方程为______________(2)据国家统计局公布的数据,浙江省2001年全省实现生产总值6700亿元,2003年生产总值达9200亿元,求浙江省这两年实现生产总值的年平均增长率.
设年平均增长率为x,可列出方程为______________2.用试验的方法探索情景一中所列方程x(x+10)=900的解，方程有几个解？都是情景一的解吗？组1： 900=2×2×3×3×5×5
900=36×25 或 900=(-36)×(-25) ··· ···组
2：布置作业：课本第27页习题1、2、3本课小结：1、只含有一个未知数，并且未知数的最高次数是2的整式方程，叫做一元二次方程。
2、一元二次方程的一般形式为ax2＋bx＋c＝0(a≠0），一元二次方程的项及系数都是根据一般式定义的，这与多项式中的项、次数及其系数的定义是一致的。
3、在实际问题转化为数学模型（ 一元二次方程 ） 的过程中，体会学习一元二次方程的必要性和重要性。